Relativité générale. L'énergie comme dimension supplémentaire dans la solution Schwarzschild

Habritants ! Cet article décrit comment obtenir une métrique générale qui inclut les métriques de Friedman et Schwarzschild en tant que cas particuliers.



Pour comprendre le matériel, vous avez besoin du concept de dérivés.



Imaginons que l'espace ait une quatrième dimension. Comme si le mouvement en lui enlevait une partie du mouvement de l'objet, ou vice versa. Comme si la gravité était un effet purement géométrique de la création d'un vortex sous-dimensionnel autour de tout objet avec de l'énergie.



Vous êtes probablement tombé sur une visualisation similaire de la gravité si la question vous intéresse:







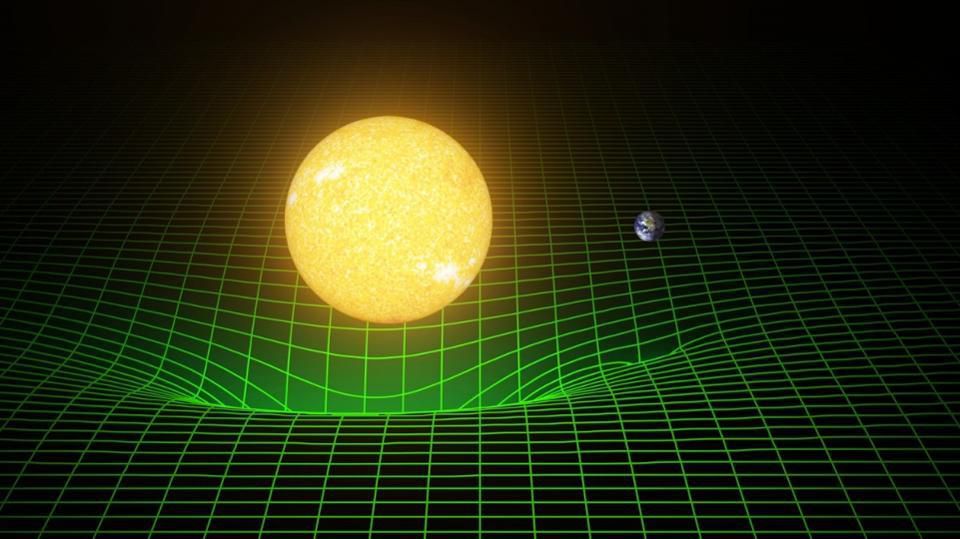
afin d'estimer la profondeur d'un tel entonnoir et le mécanisme d'interaction des objets, formulons l'expression de l'intervalle de signature (1-4).

Coordonnées à 3 sphères

Imaginez un espace en 4 dimensions $$$\psi (w,x,y,z) = \mathbb{R}^4$ , et y définir les coordonnées sphériques$$$(r, \theta, \phi, \eta)$ :

$$

$$] \, {w = r\sin\theta\sin\phi\cos\eta; \\ x = r\sin\theta\sin\phi\sin\eta; \\ y = r\sin\theta\cos\phi; \\ z = r\cos\theta } \\$$

Pour ce faire, nous écrivons la matrice de transition:

$$

$$\vec{r} = \left( \matrix{w \\ x \\ y \\ z} \right) = \left( \matrix{r\sin\theta\sin\phi\cos\eta \\ r\sin\theta\sin\phi\sin\eta \\ r\sin\theta\cos\phi \\ r\cos\theta } \right)$$

Calculons les facteurs de conversion:

$$

$$g_r = \left| \frac{\partial\vec{r}}{\partial r} \right| = \sqrt{ \left( \frac{\partial w}{\partial r} \hat{h} + \frac{\partial x}{\partial r} \hat{i} + \frac{\partial y}{\partial r} \hat{j} + \frac{\partial z}{\partial r} \hat{k} \right)^2 } = \\ = \sqrt{sin^2\theta\sin^2\phi\cos^2\eta + \sin^2\theta\sin^2\phi\sin^2\eta + sin^2\theta\cos^2\phi + \cos^2\theta} = 1 \\ g_\theta = \left| \frac{\partial\vec{r}}{\partial \theta} \right| = \sqrt{r^2cos^2\theta\sin^2\phi\cos^2\eta+r^2\cos^2\theta\sin^2\phi\sin^2\eta+r^2\cos^2\theta\cos^2\phi+r^2sin^2\theta} = \\ = \sqrt{r^2(sin^2\theta + \cos^2\theta (cos^2\phi + sin^2\phi (cos^2\eta+sin^2\eta)))} = r \\ g_\phi = \left| \frac{\partial\vec{r}}{\partial \phi} \right| = \sqrt{r^2sin^2\theta\cos^2\phi\cos^2\eta + r^2sin^2\theta\cos^2\phi\sin^2\eta + r^2sin^2\theta\sin^2\phi + 0} = \\ = \sqrt{r^2sin^2\theta} = r\sin\theta \\ g_\eta = \left| \frac{\partial\vec{r}}{\partial \eta} \right| = \sqrt{r^2\sin^2\theta\sin^2\phi\sin^2\eta+r^2\sin^2\theta\sin^2\phi\cos^2\eta} = r\sin\theta\sin\phi$$

Et présenter le correspondant $$$\psi$ intervalle:

$$

$$ds^2 = \color{red}{(-1)\cdot dt^2} + (dw^2 + \color{green}{ dx^2 + dy^2 + dz^2}) \\ ds^2 = (-1)\cdot dt^2 + (g_r^2 dr^2 + g_\theta^2 d\theta^2 + g_\phi^2 d\phi^2 + g_\eta^2 d\eta^2) \\ ds^2 = (-1)\cdot dt^2 + 1 \cdot dr^2 + r^2 \cdot d\theta^2 + r^2 \cdot \sin^2\theta \cdot d\phi^2 + r^2 \cdot \sin^2\theta \cdot \sin^2\phi \cdot d\eta^2 \\ ds^2 = \color{red}{(-1)\cdot dt^2} + \color{magenta}{1 \cdot dr^2} + \color{green}{r^2 \left( d\theta^2 + \sin^2\theta \cdot d\phi^2 + \sin^2\theta \cdot \sin^2\phi \cdot d\eta^2 \right)}$$

En rouge - la composante temporelle, présentée de la même manière que la métrique FLRW.

Vert - la composante spatiale, représentée de manière similaire à la métrique FLRW, et représentant la surface de la 3 sphère.



Le magenta s'est avéré être un lien suspendu entre le temps et l'espace - le différentiel du changement multiplicateur de la partie spatiale.

Vue générale de l'intervalle

Poursuivant le développement des idées exposées dans l' article précédent , nous plaçons le changement dans la quatrième dimension comme une mesure liée à la quantité relative d'énergie des objets, par conséquent, nous complétons la métrique du composant$$$\color{orange}{-dr^2}$en considérant un système énergétiquement fermé, ce qui sera supposé vrai à la fois pour l'Univers dans son ensemble (solution de Friedmann) et pour un corps massif sphériquement symétrique (solution de Schwarzschild). Le lecteur qui n'est pas d'accord avec cette interprétation peut simplement la considérer comme une astuce mathématique:

$$

$$ds^2 = \color{red}{(-1)\cdot dt^2 \left( 1 - \color{magenta}{\frac{dr^2}{dt^2}} \right)} + \color{green}{r^2 \left( d\theta^2 + \sin^2\theta \cdot d\phi^2 + \sin^2\theta \cdot \sin^2\phi \cdot d\eta^2 - \color{orange}{\frac{dr^2}{r^2}} \right)}$$

Le magenta dans la partie temporelle est clair:

$$

$$\color{magenta}{ \frac{dr^2}{dt^2} = \dot{r}^2 }$$

Travaillez sur les bugs. Malheureusement, présent$$$\psi'(\theta, \phi, \eta) = \mathbb{R}^3 \in \psi$à plat par la transformation des coordonnées n'est pas possible. Si vous y pensez$$$r^2 \cdot (dx^2 + dy^2 + dz^2)$les vecteurs de base ne sont plus orthogonaux les uns aux autres.

D'autres considérations ne peuvent être valables que pour le cas de l'approximation$$$\sin^2 \theta = \rho^2$ acceptable pour les grandes valeurs $$$r$...

Réformez le vert pour montrer que l'espace $$$\psi'(\theta, \phi, \eta) = \mathbb{R}^3 \in \psi$ peut être représenté en coordonnées angulaires $$$(x_1, y_1, z_1)$ comme la métrique FLRW:

$$

$$\color{green}{r^2 \left( d\theta^2 + \sin^2\theta \cdot d\phi^2 + \sin^2\theta \cdot \sin^2\phi \cdot d\eta^2 - \color{orange}{\frac{dr^2}{r^2}} \right) = \\ = r^2 \cdot dx_1^2 + r^2 \cdot \sin^2\theta \cdot \frac{d\phi^2}{d\theta^2} \cdot dy_1^2 + r^2 \cdot \sin^2\theta \cdot \sin^2\phi \cdot \frac{d\eta^2}{d\theta^2} \cdot dz_1^2 - \color{orange}{dr^2} =} \quad \rightarrow (1)$$

Dans ce cas, les coefficients de transition sont égaux:

$$

$$dx_1^2 = d\theta^2; \\ dy_1^2 = \sin^2 \theta \cdot d\phi^2 = \sin^2 \theta \cdot \frac{d\phi^2}{d\theta^2} \cdot d\theta^2 = \sin^2 \theta \cdot \left( \frac{d\phi}{d\vec{r}} \cdot \frac{d\vec{r}}{d\theta} \right)^2 \cdot d\theta^2 = \\ = \sin^2\theta \cdot \left( \frac{g_\theta}{g_\phi} \right)^2 \cdot d\theta^2 = \frac{\sin^2\theta}{\sin^2\theta} \cdot d\theta^2 = d\theta^2; \\ \frac{d\eta^2}{d\theta^2} = \frac{g_\theta^2}{g_\eta^2} = \frac{1}{\sin^2\theta \cdot \sin^2\phi };$$

Par conséquent, en tenant compte des vecteurs de base:

$$

$$(1) \rightarrow \quad \color{green}{= r^2 \cdot dx_1^2 \cdot \vec{e_{\theta}}^2 + r^2 \cdot dy_1^2 \cdot \vec{e_{\phi}}^2 + r^2 \cdot dz_1^2 \cdot \vec{e_{\eta}}^2 - \color{orange}{dr^2 \cdot \vec{e_r}^2} = } \quad \rightarrow \ (2)$$

qu'est-ce que 3 espaces $$$\psi'_1(x_1, y_1, z_1)$ avec linéaire $$$d\theta$ vecteurs de base, facteur d'échelle $$$r$ et durée instantanée $$$dl^2 = dx_1^2 + dy_1^2 + dz_1^2$, dans notre cas, collectivement réduit de la valeur $$$dr^2/r^2$:

$$

$$(2) \rightarrow \quad \color{green}{ = r^2 \cdot \left( dx_1^2 \cdot \vec{e_\theta}^2 + dy_1^2 \cdot \vec{e_\phi}^2 + dz_1^2 \cdot \vec{e_\eta}^2 - \color{orange}{\frac{dr^2}{r^2} \cdot \vec{e_r}^2} \right) = } \quad \rightarrow \ (3)$$

Sans la composante orange, nous obtenons la partie spatiale de l'intervalle du modèle cosmologique standard pour un espace «plat» avec une possible dégradation du facteur d'échelle spatiale $$$r$dans le temps, comme dans FLRW.



"Pack" supplémentaire$$$dr^2$ sera à nouveau plus pratique en sphérique, maintenant seulement habituel pour une sphère tridimensionnelle $$$(x_1, y_1, z_1) \rightarrow(\rho, \varphi, \zeta)$... Pour distinguer les coordonnées des systèmes 3 sphériques et 2 sphériques, ces derniers sont notés$$$(\rho, \varphi, \zeta)$:

$$

$$(3) \rightarrow \quad \color{green}{ r^2 \cdot \left( dx_1^2 + dy_1^2 +dz_1^2 - \color{orange}{\frac{dr^2}{r^2}} \right) = r^2 \cdot \left( d\rho^2 - \color{orange}{\frac{dr^2}{r^2}} + \rho^2 \cdot d\varphi^2 + \rho^2 \cdot \sin^2 \varphi \cdot d\zeta^2 \right) = \\ = r^2 \cdot \left( \left(1 - \color{orange}{\frac{d(\ln r)^2}{d\rho^2}} \right) d\rho^2 + \rho^2 \cdot ( d\varphi^2 + \sin^2 \varphi \cdot d\zeta^2) \right) }$$

où l'ordre de grandeur du rapport $$$dr = r d\rho \ \Rightarrow r = e^\rho$, et $$$\varphi, \zeta$ par le théorème tangent:

$$

$${ d\varphi = \frac{r}{\rho} \cdot d\phi; \\ d\zeta = \frac{r \cdot \sin \phi}{\rho \cdot \sin\varphi} \cdot d\eta. }$$

Ensuite, l'intervalle complet sera:

$$

$$ds^2 = \color{red}{(-1)\cdot dt^2 \left( 1 - \color{magenta}{\frac{dr^2}{dt^2}} \right)} + \color{green}{ r^2 \cdot \left( \left(1 - \color{orange}{\frac{d(\ln r)^2}{d\rho^2}} \right) d\rho^2 + \rho^2 \cdot ( d\varphi^2 + \sin^2 \varphi \cdot d\zeta^2) \right)} \qquad (A)$$

Le résultat est un intervalle combiné, comme s'il était "bricolé" sous la forme d'un intervalle de la métrique FLRW et de la métrique Schwarzschild, dont chacune représente un cas particulier d'interactions physiques. Voyons maintenant comment$$$(A)$ des solutions correspondantes sont obtenues.

Vue d'intervalle pour la métrique de Friedman

Purement mathématiquement, un intervalle de la forme $$$(A)$ devient la métrique FLRW du modèle cosmologique standard en excluant simplement la composante énergétique $$$dr = 0$:

$$

$$ds^2 = \color{red}{(-1)\cdot dt^2} + \color{green}{ r^2 \cdot \left( d\rho^2 + \rho^2 \cdot ( d\varphi^2 + \sin^2 \varphi \cdot d\zeta^2) \right)}$$

Ce qui, comme indiqué ci-dessus, peut également être réécrit comme ceci:

$$

$$ds^2 = \color{red}{(-1)\cdot dt^2} + \color{green}{ r^2 \cdot \left( dx^2 + dy^2 + dz^2 \right)}$$

La solution des équations de relativité générale pour un tel intervalle donne la dépendance $$$r \propto t^{2/3}$...



Cependant, les données empiriques QCS pour les objets$$$z>0.3$montrent l'écart consolidé par rapport à cette relation.



Peut-être une solution pour un intervalle comme$$$(A)$ donnera une relation plus précise, mais je ne l'ai pas encore trouvée.

Solution de relativité générale en termes de métrique de Schwarzschild

Comparons l'intervalle résultant avec la métrique de Schwarzschild :

$$

$$ds^2 = -\color{red}{(1-\frac{\rho_s}{\rho})} \cdot dt^2 + \color{orange}{\frac{1}{1 - \frac{\rho_s}{\rho}}} \cdot d\rho^2 + \rho^2 \cdot d\phi^2 + \rho^2 \sin^2 \phi \cdot d\zeta^2$$

Si on imagine un système d'objets en interaction à une échelle de basse énergie $$$(dr/r \rightarrow \infty)$puis $$$r$ peut être pris égal à un sans perdre la connectivité mathématique, l'espace deviendra alors pseudo-euclidien, et l'intervalle $$$(A)$ peut être réécrit comme suit:

$$

$$ds^2 = (-1)\cdot \color{red}{ \left( 1 - \frac{dr^2}{dt^2} \right) } \cdot dt^2 + \color{orange}{ \left(1 - \frac{dr^2}{d\rho^2} \right) } \cdot d\rho^2 + \rho^2 \cdot ( d\varphi^2 + \sin^2 \varphi \cdot d\zeta^2)$$

Mathématiquement, c'est exactement la même chose que si nous faisions le tour $$$\pm dr^2$ pour 3 espaces vides en coordonnées sphériques $$$(\rho, \varphi, \zeta)$...



Autrement dit, pour le cas du vide plat, l'intervalle$$$(A)$aura une solution similaire à la solution de la métrique de Schwarzschild, à condition que les facteurs surlignés en rouge et en orange soient équivalents. Nous obtenons le système:

$$

$$1-\frac{\rho_s}{\rho} = 1 - \frac{dr^2}{dt^2}; \\ \frac{1}{1 - \frac{\rho_s}{\rho}} = 1 - \frac{dr^2}{d\rho^2}.$$

Où $$$t, r, \rho$- dans l'ordre: temps, courbure (énergie), rayon (distance) dans un champ gravitationnel sphérique symétrique le long de la courbure totale nulle de l'espace.

En utilisant de simples transformations mathématiques, nous obtenons une solution très laconique:

$$

$$-dt^2 + dr^2 - d\rho^2 = 0,$$

ce qui confirme que:

1. La quatrième coordonnée est linéaire à la coordonnée radiale.
2. La quatrième coordonnée est la coordonnée de l'axe imaginaire.

Le premier, à mon avis, est très important car il montre que l'énergie présentée comme un axe supplémentaire est presque isotrope aux observables. Deuxièmement, cela vous permet de comprendre pourquoi elle se manifeste différemment. Et "inobservable".



De plus, je voudrais noter que la mise même dans l'intervalle d'énergie avec un signe négatif par rapport à l'espace et positif par rapport au temps nous permet de formuler leur relation comme suit: l'espace est énergie-temps, il est dépassé en énergie-temps.

Résumé

Il me semble que la poursuite du cours sur la géométrisation de la physique se révèle être une direction très prometteuse. Le caractère fictif de l'axe énergétique en cosmologie pourrait servir de tremplin aux équations de Maxwell.

Notes marginales. Pour l'avenir, je me permettrai de supposer qu'une seule mesure imaginaire pour organiser les mécanismes de charge et de masse ne suffira pas. Plus le dualisme électromagnétique comme argument en faveur d'au moins deux dimensions. Et une certaine symétrie sous la forme: dimension temporelle + deux énergétiques = trois espaces.

En passant à la micro-échelle, je vais essayer de me déplacer dans le sens du «fractionnement»$$$r$:

$$

$$ds^2 = - dt^2 - dv^2 - dw^2 + dx^2 + dy^2 + dz^2$$

Remarque 23/08/2020:

Axe imaginaire supplémentaire $$$r$ était à l'origine donné par le signe avec lequel $$$\pm dr^2$ont été divisés en composantes temporelles et spatiales. Autrement dit, si nous imaginons le champ gravitationnel non pas comme un entonnoir, mais comme une colline, alors la quatrième dimension se révélera co-dirigée vers l'espace:

$$

$$dt^2 + dr^2 + d\rho^2 = 0$$

Une telle indifférence des propriétés montrées en (1,3) par rapport à la direction du cinquième axe, apparemment, est un signe de sa forme fermée.