
Autres articles du cycle
La théorie formelle de la modélisation utilise des relations algébriques, en les incluant dans les signatures de modèles de structures algébriques, qui décrivent des objets physiques, techniques et informationnels réels, les processus de leur fonctionnement. Parmi ces derniers, j'inclus, par exemple, des bases de données (bases de données relationnelles (RDB)). Je considère que le domaine de la prise de décision n'est pas moins important, qui se compose de deux principaux statistiques et algébriques, entièrement basés sur la théorie des relations. Le niveau de formation des spécialistes de cette théorie est proche de zéro.
Ouvrez le manuel sur la spécialisation et vous y verrez, au mieux, des équivalences, que les auteurs interprètent d'une manière très particulière. Je pose la question à un DTN déjà défendu: considérez-vous la relation d'équivalence en n'indiquant ni le porteur de la relation, ni une relation spécifique, à quoi cela ressemble-t-il dans votre dossier? Réponse: à quoi ça ressemble - généralement. Il s'avère qu'il a une idée très vague de tout cela.
J'ai du mal à nommer des publications sur la conception d'une ReDB, sauf pour les articles étrangers. Dans les années 90, il était un adversaire, rédigeait une critique d'une thèse, qui considérait les bases de données hiérarchiques, en réseau et relationnelles. Mais un an, un an et demi, le travail est revenu pour examen, l'auteur n'écrit déjà que sur la DB, sur la normalisation des relations DB, mais ne montre pas de nouveauté théorique. De nombreuses universités enseignent un cours sur les bases de données, mais pas sur la façon de les créer, de créer un SGBD, mais, en règle générale, sur la façon d'exploiter une base de données prête à l'emploi (étrangère).
Tour. le personnel n'est pas prêt à enseigner aux informaticiens à créer des SGBD, OS, langages de programmation nationaux, sans parler de LSI, VLSI, LSI personnalisé. Ici, apparemment, le train est parti pour longtemps et pour longtemps. Donc, en vain, certaines joues sont gonflées de fierté (lire snobisme), cela peut être vu dans les commentaires sur les publications d'autres personnes, montrez-vous que vous pouvez, et ne vous livrez pas à des traductions et des réécritures inutiles de quelqu'un d'autre pour des raisons de fierté - «note» et «karma» Affecte non seulement le manque de créativité, mais une éducation et une éducation simples.
Le deuxième domaine qui est inextricablement lié aux relations est la prise de décision. Chacun de nous est constamment occupé avec cela. Nous ne lèverons pas le petit doigt sans une décision du conscient ou de l'inconscient. Peu de gens comprennent et encore moins écrivent sur les solutions. La décision de tout décideur (décideur) est basée sur la préférence pour les alternatives. Et le modèle de préférence est précisément ce type de relation, que l'on appelle «l'espace des relations de préférence». Mais qui les étudie. Quand je suis arrivé à un «spécialiste» des relations avec une question sur le nombre de relations de chaque type, lui, ne connaissant pas la réponse, «tué» avec une contre-question, pourquoi en avez-vous besoin?
Concept de relation
Je pense que le terme attitude est familier à tous les lecteurs, mais demander une définition sera plus déroutant. Il y a plusieurs raisons à cela. Il s'agit le plus souvent d'enseignants qui, s'ils ont utilisé des relations dans le processus d'enseignement, ne se sont pas concentrés sur ce terme, n'ont apparemment pas cité d'exemples mémorables.
Dans ma mémoire, il y a plusieurs exemples mémorables pour toute une vie. À propos des mappages et des relations. Je vais d'abord parler des mappages. Il y a deux seaux de peinture. Dans un blanc, dans l'autre - noir. Et il y a une boîte de cubes (beaucoup). Les visages ont des numéros en relief. De combien de façons pouvez-vous colorier les faces des cubes en deux couleurs? La réponse est inattendue - jusqu'à 6 nombres binaires, ou 2 6= 64. Permettez-moi d'expliquer plus en détail f: 2 → 6 2 objets sont affichés en 6. Chaque ligne du tableau est un affichage discret de fi.
Construisons un tableau avec 6 colonnes et les couleurs correspondront au nombre blanc - zéro, noir - un, et les faces du cube sont des colonnes. Nous commençons par le fait que les 6 faces sont blanches - il s'agit d'un vecteur zéro à 6 dimensions. La deuxième ligne est une face noire, c'est-à-dire que le bit le moins significatif est rempli de 1. et ainsi de suite jusqu'à ce que les nombres binaires de 6 bits soient épuisés. Nous mettons les cubes dans une longue rangée commune. Chacun d'eux semble avoir un nombre de 0 à 63.
L'affichage est maintenant inversé. Un paquet de feuilles de papier (plusieurs) et 6 peintures (feutres).
Marquez les deux côtés des feuilles de papier avec des feutres de couleurs différentes. Combien de feuilles sont nécessaires. Réponse f: 6 → 2 ou 6 2 = 36. Ce sont des mappages arbitraires.
Passons aux relations. Commençons par un ensemble abstrait - le porteur de la relation
A = {a1, a2, a3, ..., an}.
Vous pouvez en savoir plus ici . Pour une meilleure compréhension, nous réduirons l'ensemble à 3 éléments, soit = {a1, a2, a3}. Nous effectuons maintenant la multiplication cartésienne × = 2 ,
× = {(a1, a1), (a1, a2), (a1, a3), (a2, a1), (a2, a2), (a2, a3 ), (a3, a1), (a3, a2), (a3, a3)}.
Nous avons obtenu 9 paires ordonnées d'éléments de A × A, dans une paire le premier élément du premier facteur, le second du second. Essayons maintenant d'obtenir tous les sous-ensembles du carré cartésien A × A. Tout d'abord, un exemple simple.
Exemple 1... Un ensemble A = {a, b, c, d} de 4 éléments est donné. Écrivez tous ses sous-ensembles. B (A) = {Ø}; {a}; {b}; {c}; {d}; {ab}; {ac}; {ad}; {bc}; {bd}; {cd}; { abc}; {abd}; {acd}; {bcd}; {abcd}; 2 4 = 16 sous-ensembles. Il s'agit du booléen B (A) de l'ensemble A et il comprend un sous-ensemble vide.
Les sous-ensembles contiendront de A × A un nombre différent d'éléments (paires): un, deux, trois, et ainsi de suite jusqu'aux 9 paires, nous incluons également l'ensemble vide (Ø) dans cette liste. Combien de sous-ensembles y a-t-il? Beaucoup, à savoir 2 9 = 512 éléments.
Définition . Tout sous-ensemble du produit cartésien (nous avons un carré) d'un ensemble est appelé une relation . Notez que l'œuvre utilise le même ensemble. Si les ensembles sont différents, il n'y a pas de relation, mais une correspondance...
Si c'est un produit cartésien de deux facteurs, alors la relation est binaire , si de 3 elle est interne, de 4 elle est tétrare, et de n elle est n-aire. Arity est le nombre de places dans une relation. Les relations portent le nom des lettres majuscules R, H, P, S ... Arrêtons-nous sur les relations binaires (BO), car elles jouent un rôle très important dans la théorie des relations. En fait, tous les autres peuvent être réduits à des relations binaires.
Le symbole de relation est placé à gauche des éléments R (x, y) ou entre eux x R y; x, y є A.
Définition L' ensemble de tous les sous-ensembles de l'ensemble A est appelé un booléen. Notre booléen est composé de 2 | A × A | éléments, ici | A × A | Est la cardinalité de l'ensemble.
Les relations peuvent être définies dans différentes représentations sur = {a1, a2, a3, a4}:
- énumération des éléments; R1 = {(a1, a2), (a1, a3), (a2, a3) (a2, a4) (a3, a2) (a3, a4}
- binaire n = vecteur 16 bits; <0110001101010000>;
- matrice;

Graphique 1.2. a) matrice 4 × 4 de relation binaire b) numérotation des cellules de la matrice

- Représentation vectorielle. Un vecteur binaire pour représenter une relation binaire est formé à partir des éléments {0,1} comme suit:


- Représentation graphique.
Associons les éléments de l'ensemble A = {x1, x2, z3, ..., xn} aux points du plan, c'est-à-dire les sommets du graphe G = [Q, R].
Tracez un arc dans le graphe de (xi) à (xj) si et seulement si la paire (xi, xj) є R (pour i = j, l'arc (xi, xi) se transforme en boucle au sommet (xi). Exemple (Fig. 1a) la représentation d'une relation binaire A [4 × 4] par un graphe est représentée sur la Fig.2.2.

Catalogue de relations binaires (n = 3)
Grand est vu à distance. Pour avoir une idée de leur diversité, j'ai dû créer manuellement un catalogue de relations binaires sur un ensemble de 3 éléments, qui comprenait toutes les relations (plus de 500 relations). Après cela, la relation est venue ou s'est déroulée.
Évidemment, le catalogue comprendra 2 3 × 3 = 2 9relations, et chacun d'eux sera équipé d'un ensemble de propriétés inhérentes. Ci-dessous (tableau 3) une liste complète des 512 relations sur l'ensemble A, | A | = 3, de trois éléments. Les résultats du calcul du nombre de rapports (tableau 2), représentés par des combinaisons des nombres de cellules du carré cartésien 3 × 3, de différentes sous-classes pour différentes valeurs de la cardinalité de l'ensemble de porteurs (n = 3) sont également donnés. Pour chaque relation, ses propriétés de base et son appartenance au type sont indiquées (tableau 3). Les abréviations utilisées dans le catalogue sont présentées dans le tableau 2,
tableau 2. Caractéristiques quantitatives du catalogue pour différents n

Il convient d'expliquer l'essence des opérations avec des relations et leur technique à l'aide d'exemples particulièrement simples et compréhensibles pour les relations binaires. Les opérations peuvent impliquer deux et / ou plusieurs relations. Les opérations effectuées sur les relations individuelles sont des opérations unaires. Par exemple, des opérations d'inversion (obtention inverse) d'une relation, prise d'un complément, rétrécissement (limitation) d'une relation. Un exemple illustrera comment utiliser le catalogue.
Exemple 2 . Considérez la ligne Npr = 14 de la table de catalogue. Il a la forme

Les 9 premiers caractères de la ligne (à droite de l'égalité) sont un vecteur binaire correspondant à une combinaison de 9 à 2, à savoir, le numéro de la première cellule (en comptant de gauche à droite) est le numéro de la 5ème cellule de la matrice de la relation binaire, c'est-à-dire éléments a1a1 = a2a2 = 1. Cette combinaison a un nombre ordinal Ncc = 4 et un nombre passant Npr = 14 dans la liste de toutes les relations. Le reste de cette ligne contient des zéros ou des uns. Les zéros indiquent l'absence d'une propriété correspondant au nom de la colonne zéro, et les uns indiquent la présence d'une telle propriété dans la relation considérée.
Propriétés et caractéristiques quantitatives des relations
Considérons les propriétés les plus importantes des relations, ce qui nous permettra de mettre davantage en évidence les types (classes) de relations utilisées dans les bases de données relationnelles dans la théorie du choix et de la prise de décision et d'autres applications. Dans ce qui suit, nous désignerons la relation par le symbole [R, Ω]. R est le nom de la relation, Ω est l'ensemble des porteurs de la relation.
1. Réflexivité. La relation [R, Ω] est dite réflexive si chaque élément de l'ensemble est dans la relation R avec lui-même (Fig. 2.3). Le graphe d'un BO réflexif a des boucles (arcs) à tous les sommets, et la matrice de relations contient (E) la diagonale principale de l'unité.

Graphique 2.3. Attitude réflexive
2. Anti- réflectivité . La relation [R, Ω] est dite antireflet si aucun élément de l'ensemble n'est dans la relation R avec lui-même (Fig. 2.4). Une relation antireflet est appelée stricte.

Graphique 2.4. Attitude
antireflet 3. Réflexivité partielle. La relation [R, Ω] est dite partiellement
réflexive si un ou plusieurs éléments de l'ensemble ne sont pas dans la relation R avec lui-même (Fig. 2.5).

4. Symétrie. Une relation [R, Ω] est dite symétrique si, avec une paire ordonnée (x, y), la relation contient également une paire ordonnée (y, x) (Fig. 2.6).

5. Antisymétrie. Une relation [R, Ω] est dite antisymétrique si, si, pour toute paire ordonnée (x, y) є R, une paire ordonnée
(y, x) єR, uniquement dans le cas x = y. Pour de tels rapports R∩R -1 ⊆ E (Fig. 2.7).

6. Asymétrie. Une relation [R, Ω] est dite asymétrique si elle est antireflet et pour toute paire ordonnée (x, y) є R une paire ordonnée (y, x) ∉ R, pour les relations R ∩ R -1 = Ø (Fig. 2.8).

7. Transitivité. La relation [R, Ω] est dite transitive si pour toute paire ordonnée (x, y), (y, z) є R, dans la relation R il y a une paire ordonnée (x, z) є R ou si R × R⊆R (Fig . 2.9).

8. Cyclicité. Une relation [R, Ω] est dite cyclique si pour ses éléments {x1, x2, z3, ..., xn} il existe un sous-ensemble d'éléments {xi, xi + 1, ... xr, ..., xj, xi}, pour laquelle on peut écrire la séquence xiRxi + 1R ... RxjRxi. Une telle séquence est appelée cycle ou boucle (Figure 2.10).

9. Acyclicité. Les relations dans lesquelles il n'y a pas de contours sont appelées acycliques. Pour les relations acycliques, la relation R k ∩R = Ø pour tout k> 1 est vérifiée (Fig. 2.11).

10. Complétude (connectivité). La relation [R, Ω] est dite complète (connexe) si pour deux éléments quelconques (y, z) є Ω l'un d'eux est en relation avec l'autre (Fig. 2.12). Linéarité. Les relations linéaires sont des relations peu complètes.

Graphique 2.12. Relation linéaire
Ainsi, nous avons établi que les relations, en tant qu'objets mathématiques, ont certaines propriétés dont la définition est donnée plus tôt. Dans le paragraphe suivant, nous examinerons l'essence et la manifestation de certaines propriétés:
- Réflexivité x є A (xRx).
- Antireflexivité x є A ¬ (xRx).
- Symétrie x, y є A (xRy → yRx).
- Antisymétrie (xRy & yRx → x = y).
- Transitivité; x, y, z є A (xRy & yRz → xRz).
- Cyclicité; x, y є A; ...
- Complétude x, y є (xRy, yRx);
- Connectivité (x ≠ y → xRy, yRx).
- Linéarité x, y є (xRy, yRx).
L'analyse de l'espace des relations est une tâche complexe de la théorie et, il faut le noter, est loin d'être achevée. Les principaux résultats devraient inclure la sélection de sous-ensembles de relations qui forment des espaces complets de relations avec toutes les conséquences qui en découlent.
Les relations quantitatives de ces espaces discrets présentent un grand
intérêt à la fois théorique et pratique. Certains aspects des caractéristiques quantitatives associées aux propriétés des relations de différents types sont examinés ci-dessous.
Opérations sur les relations
Comme la plupart des systèmes de nombres avec relations, les opérations suivantes sont effectuées:
- unaire;
- binaire;
- à peine.
Vous trouverez ci-dessous des tableaux d'addition et de multiplication booléenne et de deux variables x1 et x2, l'addition de mod 2 et la sommation binaire:

Ci-dessus, le concept d'une relation binaire a été introduit, comme un sous-ensemble de paires ordonnées du produit cartésien d'ensembles, et les propriétés des relations ont également été considérées. De plus, les relations binaires et la représentation matricielle des relations ont été mentionnées. Examinons maintenant le concept de relation plus en détail, en outre, considérons les opérations de base des relations binaires, les plus importantes de leur ensemble pour les relations.
Pour eux, les conditions suivantes doivent être remplies:
- L'arité des opérandes de l'opération doit correspondre;
- le résultat de l'opération doit être une relation de même arité.
Pour les relations binaires et n-aires, les conditions suivantes doivent être satisfaites: la zone d'arrivée du premier opérande doit correspondre à la zone d'origine du second opérande.
Opérations unaires sur les relations
Inversion des relations . L'inverse du rapport R est le rapport R -1 défini par la condition xR -1 y <=> yRx. Plus correctement, cette opération doit être appelée pseudo-inversion, puisque p · p -1 ≠ E = Δ.
Soit la relation s'écrire sous la forme d'une liste des paires ordonnées qu'elle contient. Si les composants sont interchangés dans chaque paire, alors les nouvelles paires forment le rapport P -1 , qui est appelé l'inverse de P.
La relation inverse à la relation P est la relation formée par les couples (ai aj) pour lesquels (aj ai) є P -1 . Pour les relations sous forme matricielle, les relations inverses sont obtenues par transposition de la matrice P.
9. La relation duelle (P d ) à la relation P est la relation formée par toutes les paires qui appartiennent à la relation universelle et n'appartiennent pas à la relation inverse (addition à l'inverse):
P d = {(ai aj) | ((ai aj) єA × A) & (ai aj) ∉ P -1 )} = (A × A) \ P -1 .
Les relations duales et inverses dans l'agrégat contiennent toutes les paires du produit cartésien A × A et n'ont pas de paires communes, elles, comme les relations P et P former une partition A × A

Notez que pour toute relation P n'est pas satisfaite P P = d .
Rétrécissement (PA1). La relation [R1, A1] est appelée la restriction de la relation [R, A] à l'ensemble Ω1 si Ω1⊆ Ω et R1 = R∩Ω1 × Ω1. Le rapport PA1 sur l'ensemble A1 ⊆ A est le rapport PA1 sur l'ensemble A1, formé de toutes les paires appartenant à la relation P et faisant simultanément partie du produit cartésien A1 × A1. En d'autres termes, PA1 est l'intersection des relations P et A1 × A1. Soit A1 = {a1, a3, a4}, alors pour les relations P et Q sous forme matricielle, les relations de rétrécissement auront la forme:

Opérations binaires Les opérations
nécessitant au moins deux relations sont n-aires (n-aires). Seules des relations de même arité peuvent participer à de telles opérations. Exemples de telles opérations: intersection, union, différence, différence symétrique des relations, et quelques autres. Si l'opération utilise plus de deux relations, elle est exécutée séquentiellement pour les deux premières, puis pour la relation finale et la troisième, etc.
En d'autres termes, ces opérations sont définies pour deux relations. Dans les opérations sur les relations, on suppose que les domaines de spécification des relations (opérandes et résultat) coïncident, les arités des relations coïncident, et le résultat de l'opération est à nouveau une relation de même arité. A titre d'exemples, nous considérerons les opérations sur les relations binaires P et Q définies sur un ensemble discret
= {a1, a2, a3, a4} par matrices booléennes (en règle générale, les zéros ne rentrent pas dans la matrice):

1. L'intersection (P ∩ Q) est une relation formée par toutes ces paires d'éléments de A qui sont incluses dans les deux relations, ie commun à P et Q,
P ∩ Q = {(ai aj) | ((ai aj) є P) & ((ai aj) є Q)}.
La matrice de rapport P ∩ Q est obtenue comme l'intersection booléenne des matrices P et Q:

En l'absence de telles paires communes, l'intersection des relations est dite vide, c'est-à-dire c'est une relation nulle. L'intersection des relations R1 et R2 (R1∩R2) est la relation déterminée par l'intersection des sous-ensembles correspondants de A × A.
2. Union (PUQ). L'union des relations R1 et R2 (R1UR2) est la relation définie par l'union des sous-ensembles correspondants de A × A. Le rapport formé par toutes les paires qui composent soit le rapport P, soit le rapport Q, c'est-à-dire par paires appartenant à au moins une des relations (le connectif ∨ - ou l'unifiant)
PUQ = {(ai aj) | ((ai aj) є P) ∨ ((ai aj) є Q)}.
Si dans l'ensemble A × A il n'y a pas d'autres paires qui ne sont pas incluses dans la relation PUQ et que leur intersection est nulle, alors les relations P et Q sont dites former une relation complète A × A lorsqu'elles sont combinées, et leur système est une partition de cette relation complète. L'union des matrices de relations est formée comme une somme booléenne des matrices de relations:

3. La différence (P \ Q) est le rapport formé par les paires de P qui ne sont pas incluses dans la relation Q
P \ Q = {(ai aj) | ((ai aj) є P) & ((ai aj) ∉Q)}.
La différence pour les relations dans la représentation matricielle est

4. Multiplier les relations. Les paires ordonnées formant une relation peuvent contenir ou non les mêmes éléments. Parmi les paires qui ont des éléments identiques dans leur composition, distinguons ces paires ordonnées, que nous appelons adjacentes (contiguës) et qui ont le 1er élément de la seconde paire, et le 2ème élément de la première paire est le même. Définissons le produit des paires adjacentes comme une paire ordonnée:
(ai ak) ∙ (ak aj) => (ai aj).
En termes de théorie des graphes, cela signifie que les paires adjacentes forment un itinéraire du point (ai) au point (aj) en transit par le point (ak), qui se compose de 2 arcs adjacents. Le produit de ces arcs est le troisième arc du point (ai) au point (aj), qui met en œuvre la transition entre les points extrêmes de l'itinéraire dans la même direction, en contournant le point intermédiaire (ak). On dit que l'arc (ai aj) ferme ces points directement.
5. Différence symétrique (P∆Q) - le rapport formé par les paires qui sont incluses dans l'union PUQ, mais ne sont pas incluses dans l'intersection P∩Q. Une autre forme de définition explique le nom de l'opération: P∆Q est formé par ces paires ordonnées qui sont l'union des différences P \ Q et Q \ P. Ainsi, l'expression de la différence symétrique peut s'écrire de deux manières différentes:
P∆ Q = (PU Q) \ (P ∩ Q) = (P \ Q) U (Q \ P).
La matrice des différences symétriques est:

Du dernier enregistrement, il s'ensuit que l'opération de différence symétrique permet la permutation des opérandes, c'est-à-dire qu'elle est commutative.
5. Composition ou produit (P ∙ Q) - la relation formée par toutes les paires pour lesquelles:
P ∙ Q = {(ai aj) | ((ai ak) є P) & ((ak aj) є Q)}.
En d'autres termes, chaque paire ordonnée dans la relation résultante est le résultat de la multiplication de paires adjacentes, dont la 1ère paire appartient à la première relation factorielle, la 2ème - à la seconde relation factorielle. L'opération de composition n'est pas commutative.
La composition (◦Q) sur un ensemble M est une relation R définie sur le même ensemble M qui contient un couple (x, y) lorsqu'il existe Z є M tel que (x, z) є P et (z, y) є Q.
Dans la représentation matricielle des relations, la matrice de composition des relations est égale au produit booléen des matrices des relations d'origine:

Un cas particulier de la composition des relations est le carré de la relation.
On peut montrer par récurrence que le nième degré d'une relation est défini récursivement par la formule: P n = P n-1 ◦, cela signifie que le couple (x, y) є P n dans le cas où la matrice contient une chaîne éléments: tels que (xi, xi + 1) є P, 1 <i <n - 1.
L'opération de composition a la propriété d'associativité (comme un produit de matrices).
La composition des relations sur l'ensemble M est le résultat d'une composition par paires de relations pour tout arrangement de parenthèses. La zone de réglage du résultat de la composition ne change pas.
La composition des matrices booléennes de relations est formée à la suite du produit booléen des matrices de ces relations.
Tableau 3. Catalogue des relations binaires (n = 3). Cliquable


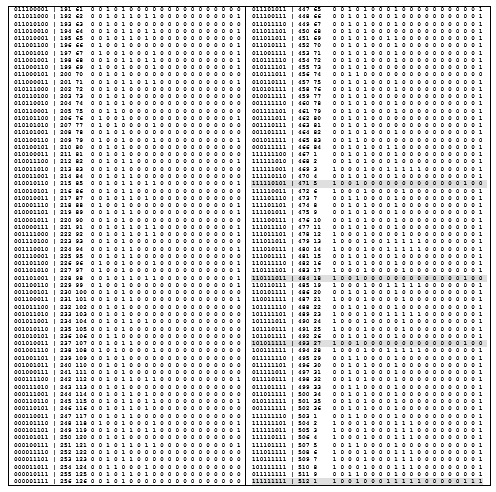
Littérature
1. .., .. . , , . — .: , 2017. -352 .
2. .. ., , - .: .. ., 2001. -352 .
3. .. .- .: , 2003. -960 .
4. . . -.: ,1971.- 478 .
5. .. . 1- .: . .. , 2015. -219 .
6. .. . 2- .: . .. , 2017. -151 .
7. . . .-.: ,1985.- 352 .
8. ., ., . . .-.: ,1998.-703 .
9. . . -.: ,1980. -463 .
10. .. .- .: ,2006. — 304 .
.. : -.: .. ., 2001. -280 .
11. .. : , , -.: , 2000.-280 .
12. ., . .-.: , 1973.-832 .
13. ., . : 2- . .1 -.: ,1988. — 430 .
14. ., . : 2- . .2 -.: ,1988. — 392 .
15. .., .., .., .-.: ,1967.-264 .
16. . . -.: , 1987.- 608 .
17. .. . -. ,1990.- 288 .
18. ., ., . . — .: , 1986. — 197 .
19. .. . .-.: ,1991.-352 .
20. .. .- .: .. ., 2001. -280 .
21. .. .- .: , 2000. -304 .
22. .. .-.: ,1966.-648 .
23. . . — .: ,1983.-334 .
24. . .-.: . , 1962.- 468 .
25. .. , , . — .: ,2006. — 368 .
26. .. : 2- .2.-.: . ., 1987. -256 .
27. .. .- : ,2000. -240 .
2. .. ., , - .: .. ., 2001. -352 .
3. .. .- .: , 2003. -960 .
4. . . -.: ,1971.- 478 .
5. .. . 1- .: . .. , 2015. -219 .
6. .. . 2- .: . .. , 2017. -151 .
7. . . .-.: ,1985.- 352 .
8. ., ., . . .-.: ,1998.-703 .
9. . . -.: ,1980. -463 .
10. .. .- .: ,2006. — 304 .
.. : -.: .. ., 2001. -280 .
11. .. : , , -.: , 2000.-280 .
12. ., . .-.: , 1973.-832 .
13. ., . : 2- . .1 -.: ,1988. — 430 .
14. ., . : 2- . .2 -.: ,1988. — 392 .
15. .., .., .., .-.: ,1967.-264 .
16. . . -.: , 1987.- 608 .
17. .. . -. ,1990.- 288 .
18. ., ., . . — .: , 1986. — 197 .
19. .. . .-.: ,1991.-352 .
20. .. .- .: .. ., 2001. -280 .
21. .. .- .: , 2000. -304 .
22. .. .-.: ,1966.-648 .
23. . . — .: ,1983.-334 .
24. . .-.: . , 1962.- 468 .
25. .. , , . — .: ,2006. — 368 .
26. .. : 2- .2.-.: . ., 1987. -256 .
27. .. .- : ,2000. -240 .