La géométrie symplectique est un domaine d'étude relativement nouveau, influençant une grande partie des mathématiques modernes. Et c'est ce que c'est.

Au début du 19e siècle, William Rowan Hamilton a découvert un nouvel espace géométrique aux propriétés presque magiques. Il a encodé le mouvement et les mathématiques en un seul bel objet géométrique.
De ce phénomène s'est développé un champ de connaissance appelé géométrie symplectique . Au cours des dernières décennies, il est passé de quelques collections d'idées à un champ de recherche dynamique avec des liens profonds avec plus de sujets en mathématiques et en physique qu'Hamilton n'aurait guère pu imaginer.
La géométrie symplectique est essentiellement l'étude des espaces géométriques de structure symplectique. Cependant, il faut clarifier ce que cela signifie que l'espace a une structure - sans parler d'une structure particulière.
Les espaces géométriques peuvent être flexibles comme une bâche ou rigides comme une tente. «Les bâches sont malléables, mais si vous prenez un tas de bâtons et que vous l'encadrez, vous obtenez une structure plus stable», a déclaré Emmy Murphy de l'Université Northwestern.
Les espaces moins structurés ne sont qu'un tas de points connectés (comme une bâche). La ligne droite est un exemple d'espace unidimensionnel de ce type. La surface d'une balle est un exemple bidimensionnel. Puisqu'il n'y a pas de structure dans ces espaces, il est facile de les déformer sans changer à un niveau fondamental. Courbez une ligne droite; gonfler, froisser, tordre la balle - du point de vue de la topologie, en étudiant les espaces non structurés, ils ne changeront pas.
«Du point de vue des topologues, en commençant par la surface d'une balle, vous pouvez l'étirer comme vous le souhaitez, et jusqu'à ce que vous la cassiez, cet espace ne change pas pour eux», a déclaré Isa Keating de l'Université de Cambridge. "Ils s'intéressent aux caractéristiques générales de la figure."
Naturellement, lorsque les mathématiciens parlent de la déformation de l'espace, ils ne veulent pas dire le changer manuellement. Ils changent d'espaces à l'aide de fonctions: la fonction inclut les coordonnées d'un point, et les coordonnées d'un nouveau point sortent. De telles transformations traduisent n'importe quel point de l'espace en un nouveau. C'est l'équivalent mathématique de secouer une bâche.
Vous pouvez ajouter une structure à l'espace. Cette structure renforce les informations contenues dans l'espace, tout en limitant les possibilités de sa déformation.

Espace non structuré: la surface de la balle est un espace bidimensionnel. L'absence de structure offre de nombreuses possibilités de déformation sans modifier ses propriétés topologiques.

Ajout de structures: En ajoutant une structure métrique à l'espace - disons, comme les lignes de latitude et de longitude sur un globe - nous pouvons mesurer les distances entre les points. Mais alors, il n'y aura qu'un petit ensemble d'options pour la déformation des objets qui ne violent pas ces distances.
Vous pouvez, par exemple, ajouter une structure métrique à la surface d'une sphère, comme les lignes de latitude et de longitude sur un globe. Une telle structure nous permettra de mesurer les distances entre les points. Mais après son application, il ne sera plus possible de gonfler ou de froisser la balle sans casser la structure d'origine - après tout, nous modifierons les distances entre les points. Si nous gonflons le ballon, la distance entre New York et Londres, par exemple, augmentera.
Nous pouvons ajouter un autre type de structure - symplectique. Cela nous donne la possibilité de mesurer des zones dans l'espace et nous permet de changer la forme de l'espace pour que ces zones ne changent pas.
Le premier exemple d'un tel espace a été trouvé par Hamilton lors de l' étude des systèmes physiques- par exemple, les mouvements planétaires. Lorsqu'une planète se déplace dans l'espace, son emplacement est déterminé par trois coordonnées qui déterminent sa position le long des axes x, y et z. Les points représentant tous les emplacements planétaires possibles forment un espace tridimensionnel.
Hamilton a découvert que chaque point de cet espace tridimensionnel peut se voir attribuer trois coordonnées supplémentaires, indiquant la magnitude de l'élan de la planète le long des trois axes. Appelons-les x m , y m et z m . Nous avons maintenant six coordonnées: trois pour l'emplacement et trois pour l'élan. Ces six coordonnées définissent un point dans le nouvel espace à six dimensions.

Nous avons six coordonnées: trois pour l'emplacement et trois pour l'élan. Ces six coordonnées définissent un point dans le nouvel espace à six dimensions.
Cet espace à six dimensions est un exemple d'espace avec une structure symplectique, car il a la capacité de mesurer des zones. Et voici comment cela fonctionne.
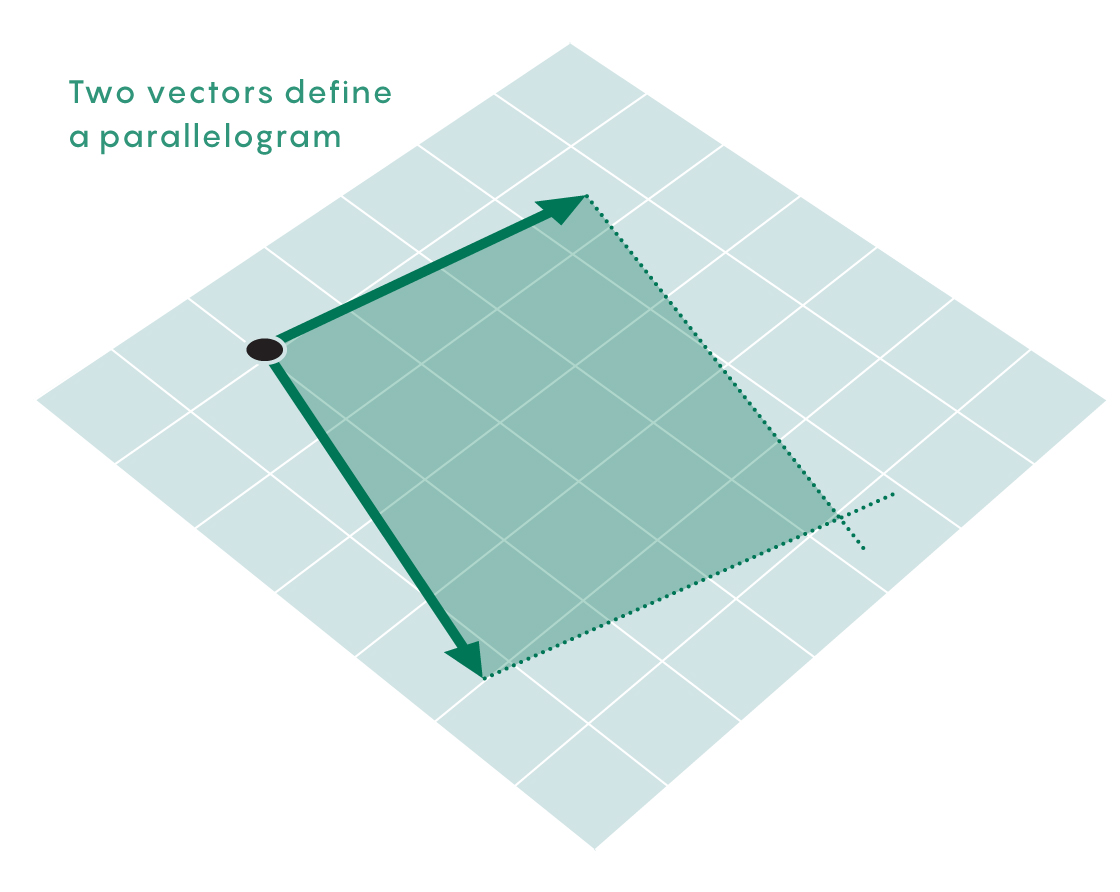
À chaque point de l'espace, vous pouvez dessiner six vecteurs (flèches directionnelles) correspondant à la direction du mouvement ou de l'élan de la planète le long de la dimension où pointe le vecteur. Puisque deux vecteurs forment un parallélogramme - un espace bidimensionnel avec une aire non nulle - vous pouvez prendre deux vecteurs et mesurer cette aire.
Pour vous assurer que la valeur est différente de zéro, vous devez prendre certaines paires de vecteurs - indiquant la direction du mouvement et l'élan le long du même axe. Des vecteurs non concordants, par exemple, le vecteur directionnel de l'axe z avec le vecteur de moment de l'axe y donnent un parallélogramme avec une aire nulle.
Ces paires de vecteurs reflètent également une autre propriété importante de l'espace symplectique - leur relation avec les nombres complexes. Ces nombres ont i, la racine carrée de -1, et sont de la forme a + bi, où a est réel et b est imaginaire. Une façon de définir un espace symplectique à six dimensions est de définir trois nombres complexes, deux parties de chacun donnant une coordonnée. Ces deux parties correspondent également aux deux vecteurs que nous combinons pour mesurer la surface.
Ainsi, pour chaque point, par exemple, les vecteurs de direction du mouvement et d'élan tracés le long de l'axe des x fournissent non seulement un moyen de mesurer la surface, mais constituent également l'un des trois nombres complexes qui définissent l'espace. Cette relation se reflète dans le nom, car «symplectique» vient du mot grec sumplektikós, qui signifie la même chose que le complexe latin - «enlacés ensemble». Le nom reflète l'entrelacement de la structure symplectique et des nombres complexes.
C'est aussi l'une des principales raisons pour lesquelles l'espace symplectique capte l'imagination des mathématiciens. «Les mathématiciens s'intéressaient déjà aux nombres complexes et aux mouvements planétaires», a déclaré Murphy. "Donc, si vous parlez à un mathématicien de l'existence de la géométrie, ce qui montre pourquoi ces deux choses sont des manifestations différentes de la même structure de base, il sera certainement intéressé par cette question."
La géométrie symplectique étudie les transformations d'espaces qui conservent leur structure symplectique et ne modifient pas la taille des zones. Cette restriction ne laisse pas beaucoup de marge de manœuvre pour les transformations autorisées. En conséquence, la géométrie symplectique occupe une position intermédiaire entre la topologie de la bâche flexible et la géométrie de la tente rigide. Les transformations qui préservent la structure symplectique sont appelées, d'après le découvreur, difféomorphismes hamiltoniens .
Cependant, Hamilton n'a découvert que le premier exemple d'un espace symplectique, et il n'y avait aucune raison de s'y attarder. Bientôt, les mathématiciens ont commencé à réfléchir à ce à quoi pourraient ressembler les phénomènes symplectiques dans des espaces géométriques sans rapport avec le monde physique.
"Les mathématiciens s'efforcent toujours de généraliser, nous voulons nous demander: à quoi ressemblerait la mécanique classique si nous ne vivions pas dans un espace en trois dimensions, mais dans un espace à huit dimensions?" Dit Murphy.

Vladimir Igorevich Arnold a avancé plusieurs hypothèses de base dans le domaine de la géométrie symplectique
Dans les années 1960, Vladimir Igorevich Arnoldont avancé plusieurs hypothèses influentes décrivant certaines propriétés de l'espace symplectique qui les rendent plus rigides que les topologiques ordinaires. L'une d'elles, la conjecture d'Arnold sur les points fixes des symplectomorphismes, prédit que les difféomorphismes hamiltoniens ont un nombre étonnamment grand de points «fixes» qui ne changent pas de position pendant les transformations. En les étudiant, nous pouvons dire exactement ce qui distingue l'espace symplectique des autres types d'espaces géométriques.
À la fin des années 1980, le mathématicien allemand Andreas Floerdéveloppé l'homologie de Floer, une plateforme puissante que les mathématiciens utilisent aujourd'hui pour étudier les phénomènes symplectiques. Elle utilise le soi-disant. courbes pseudoholomorphes, qui permettent indirectement aux mathématiciens de compter le nombre de points fixes, en déterminant un certain nombre minimum d'entre eux qu'un espace symplectique devrait avoir.
"L'homologie de Floer montre que vous ne pouvez pas simplement laisser tomber des points fixes", a déclaré Keating. "Cela vous permet de prouver que ces points doivent être là."
Au fur et à mesure que la théorie de la géométrie symplectique se développait, des liens ont été trouvés avec un éventail toujours croissant de sujets en mathématiques et en physique, de la théorie des cordes à la topologie de faible dimension et à l'étude d'une dualité mathématique déroutante appelée symétrie miroir. Un exemple récent de l'application de la géométrie symplectique est la solution du problème topologique des chevilles carrées .
Pour de nombreux mathématiciens, cependant, l'attrait de la géométrie symplectique a peu à voir avec ses intersections avec la physique ou d'autres domaines des mathématiques. Ils considèrent son existence même comme un miracle. «Nous commençons à trouver de la beauté dans la structure elle-même, indépendamment de ses liens avec quoi que ce soit d'autre», a déclaré Murphy.