HDTree: un arbre de décision personnalisé en Python

Présentation d'une structure d'arbre de décision personnalisable et interactive écrite en Python. Cette implémentation est adaptée pour extraire des connaissances à partir de données, tester l'intuition, améliorer votre compréhension du fonctionnement interne des arbres de décision et explorer d'autres relations de cause à effet pour votre problème d'apprentissage. Il peut être utilisé dans le cadre d'algorithmes, de visualisations et de rapports plus complexes, à toutes fins de recherche, et comme plate-forme accessible pour tester facilement vos idées d'algorithme d'arbre de décision.



TL; DR

• Dépôt HDTree
• Cahier complémentaire à l'intérieur examples. Le répertoire du référentiel est ici (chaque illustration que vous voyez ici sera générée dans le bloc-notes). Vous pouvez créer vous-même des illustrations.

De quoi parle le post?

Une autre implémentation d'arbres de décision que j'ai écrite dans le cadre de ma thèse. Le travail est divisé en trois parties comme suit: 

• Je vais essayer d'expliquer pourquoi j'ai décidé de prendre mon temps pour créer ma propre implémentation d'arbres de décision. Je vais énumérer certaines de ses fonctionnalités , mais aussi les inconvénients de l' implémentation actuelle.
• Je vais vous montrer l'utilisation de base de HDTree avec quelques extraits de code et quelques détails expliqués en cours de route.
• Conseils pour personnaliser et étendre HDTree avec vos idées.

Motivation et contexte

Pour ma thèse, j'ai commencé à travailler avec des arbres de décision. Mon objectif est maintenant de mettre en œuvre un modèle ML centré sur l'homme où HDTree (Human Decision Tree, d'ailleurs) est un ingrédient supplémentaire qui est appliqué dans le cadre de l'interface utilisateur réelle de ce modèle. Bien que cette histoire concerne exclusivement HDTree, je pourrais écrire une suite détaillant les autres composants.

Fonctionnalités HDTree et comparaison avec les arbres de décision scikit learn

Naturellement, je suis tombé sur une implémentation d'arbre de décision scikit-learn[4]. La mise en œuvre sckit-learnprésente de nombreux avantages:

• C'est rapide et simplifié;
• Écrit dans le dialecte Cython. Cython compile en code C (qui, à son tour, compile en code binaire), tout en conservant la possibilité d'interagir avec l'interpréteur Python;
• Simple et pratique;
• De nombreuses personnes en ML savent comment travailler avec des modèles scikit-learn. Obtenez de l'aide partout grâce à sa base d'utilisateurs;
• Il a été testé en conditions de combat (il est utilisé par beaucoup);
• Cela fonctionne simplement;
• Il prend en charge une variété de techniques de pré-coupe et de post-coupe [6] et offre de nombreuses fonctionnalités (par exemple, coupe avec un coût et des poids d'échantillons minimes);
• Prend en charge le rendu de base [7].

Cependant, cela présente certainement certains inconvénients:

• Ce n'est pas anodin à changer, en partie à cause du dialecte Cython plutôt inhabituel (voir les avantages ci-dessus);
• Il n'y a aucun moyen de prendre en compte les connaissances des utilisateurs sur le domaine ou de modifier le processus d'apprentissage;
• La visualisation est assez minimaliste;
• Pas de support pour les fonctionnalités catégorielles;
• Aucun support pour les valeurs manquantes;
• L'interface pour accéder aux nœuds et parcourir l'arborescence est lourde et peu intuitive;
• Aucun support pour les valeurs manquantes;
• Partitions binaires uniquement (voir ci-dessous);
• Il n'y a pas de partitions multivariées (voir ci-dessous).

Fonctionnalités HDTree

HDTree offre une solution à la plupart de ces problèmes, tout en sacrifiant de nombreux avantages de l'implémentation de scikit-learn. Nous reviendrons sur ces points plus tard, alors ne vous inquiétez pas si vous ne comprenez pas déjà toute la liste suivante:

• Interagit avec le comportement d'apprentissage;
• Les principaux composants sont modulaires et assez faciles à étendre (implémenter une interface);
• Écrit en pur Python (plus disponible)
• A une visualisation riche;
• Prend en charge les données catégoriques;
• Prend en charge les valeurs manquantes;
• Prend en charge le fractionnement multivarié;
• A une interface pratique pour naviguer dans la structure arborescente;
• Prend en charge le partitionnement n-aire (plus de 2 nœuds enfants);
• Représentations textuelles de solution;
• Encourage l'explicabilité en imprimant un texte lisible par l'homme.

Moins:

• Lent;
• Non testé dans les batailles;
• La qualité du logiciel est médiocre;
• Pas beaucoup d'options de recadrage. Bien que l'implémentation prenne en charge certains paramètres de base.

Il n'y a pas beaucoup d'inconvénients, mais ils sont critiques. Soyons clairs tout de suite: ne fournissez pas de big data à cette implémentation. Vous attendez pour toujours. Ne l'utilisez pas dans un environnement de production. Il peut se briser de manière inattendue. Tu as été prévenu! Certains des problèmes ci-dessus peuvent être résolus au fil du temps. Cependant, le taux d'apprentissage restera probablement faible (bien que la déduction soit valide). Vous devrez trouver une meilleure solution pour résoudre ce problème. Je vous invite à contribuer. Cependant, quelles sont les applications possibles?

• Extraire des connaissances à partir de données;
• Vérification de la vue intuitive des données;
• Comprendre le fonctionnement interne des arbres de décision;
• Explorez les relations causales alternatives en relation avec votre problème d'apprentissage;
• Utiliser dans le cadre d'algorithmes plus complexes;
• Création de rapports et visualisation;
• Utilisation à des fins de recherche;
• En tant que plateforme accessible pour tester facilement vos idées d'algorithmes d'arbre de décision.

Arborescence de décision

Bien que les arbres de décision ne soient pas abordés en détail dans cet article, nous résumerons leurs principaux éléments de base. Cela fournira une base pour comprendre les exemples plus tard, et mettra également en évidence certaines des fonctionnalités de HDTree. La figure suivante montre la sortie réelle de HDTree (à l'exclusion des marqueurs).







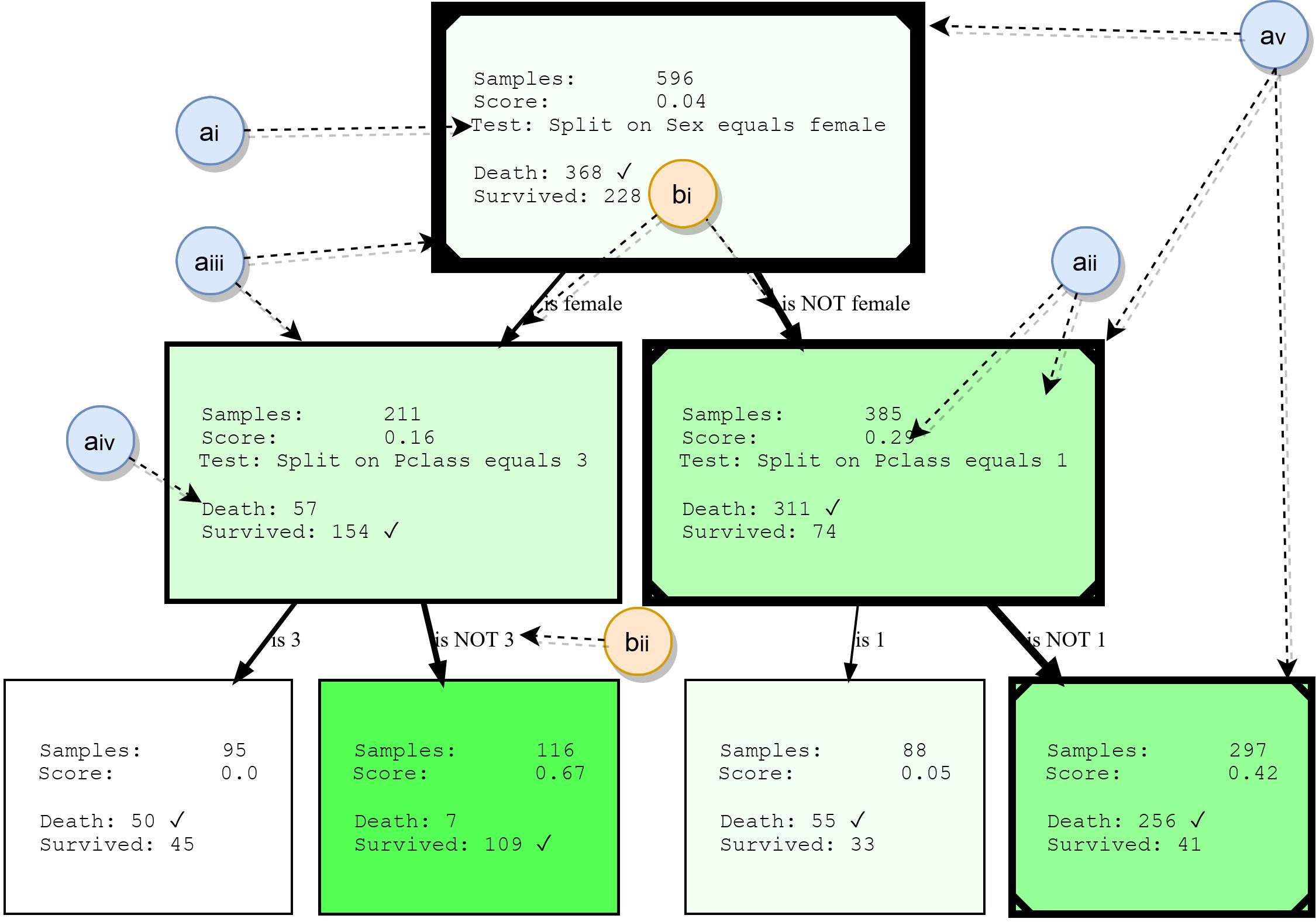
Nœuds

• ai: , . . * * . . 3.
• aii: , , , , . , . . , ( , .. ). HDTree.
• aiii: La bordure des nœuds indique combien de points de données passent par ce nœud. Plus la bordure est épaisse, plus les données transitent par le nœud.
• aiv: liste des cibles de prédiction et des étiquettes qui ont des points de données passant par ce nœud. La classe la plus courante est marquée.
• av: en option, la visualisation peut marquer le chemin que suivent les points de données individuels (illustrant la décision prise lorsque le point de données traverse l'arborescence). Ceci est marqué par une ligne dans le coin de l'arbre de décision.

Travers de porc

• bi: une flèche relie chaque résultat de fractionnement possible (ai) à ses nœuds enfants. Plus il y a de données relatives au parent "circulant" autour du bord, plus elles sont affichées.
• bii: chaque arête a une représentation textuelle lisible par l'homme du résultat divisé correspondant.

D'où viennent les différents split sets et tests?

À ce stade, vous vous demandez peut-être déjà en quoi HDTree diffère d'un arbre scikit-learn(ou de toute autre implémentation) et pourquoi nous pourrions vouloir avoir différents types de partitions? Essayons de clarifier cela. Peut-être avez-vous une compréhension intuitive de l' espace des fonctionnalités . Toutes les données avec lesquelles nous travaillons se trouvent dans un certain espace multidimensionnel, qui est déterminé par le nombre et le type de caractéristiques de vos données. La tâche de l'algorithme de classification est maintenant de diviser cet espace en zones sans chevauchement et d' attribuerces domaines sont de classe. Visualisons ceci. Puisque nos cerveaux ont du mal à bricoler avec une dimensionnalité élevée, nous nous en tiendrons à un exemple 2D et à un problème à deux classes très simple, comme ceci:







Vous voyez un ensemble de données très simple composé de deux dimensions (traits / attributs) et de deux classes. Les points de données générés étaient normalement répartis dans le centre. Une rue qui n'est qu'une fonction linéaire  f(x) = ysépare les deux classes: Classe 1 (en bas à droite) et Classe 2 (en haut à gauche). Un bruit aléatoire a également été ajouté (points de données bleus en orange et vice versa) pour illustrer les effets du surajustement par la suite. Le travail d'un algorithme de classification comme HDTree (bien qu'il puisse également être utilisé pour des problèmes de régression ) est de découvrir à quelle classe appartient chaque point de données. En d'autres termes, étant donné une paire de coordonnées (x, y)comme(6, 2)... Le but est de savoir si cette coordonnée appartient à la classe orange 1 ou bleue 2. Le modèle discriminant tentera de diviser l'espace objet (ici ce sont les axes (x, y)) en territoires bleu et orange, respectivement.

Compte tenu de ces données, la décision (règles) sur la manière dont les données seront classées semble très simple. Une personne raisonnable dirait «pensez d'abord par vous-même».

"C'est la classe 1 si x> y, sinon la classe 2." La fonction y=xpointillée créera une séparation parfaite . En effet, un classificateur de marge maximale comme les machines à vecteurs de support [8] suggérerait une solution similaire. Mais voyons quels arbres de décision résolvent la question différemment:







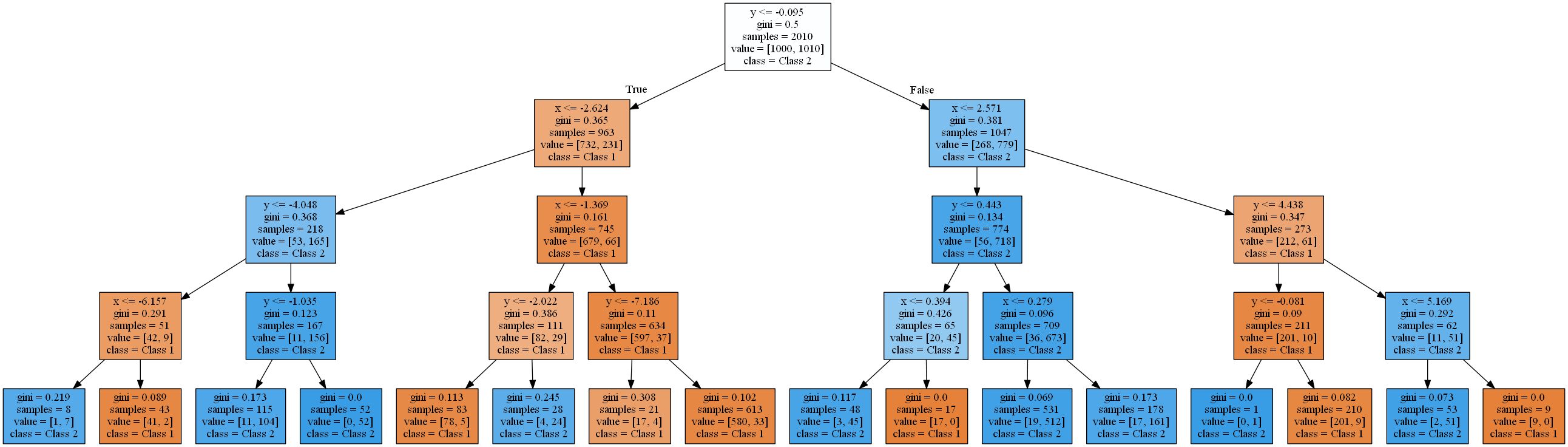
L'image montre les zones où un arbre de décision standard avec une profondeur croissante classe un point de données en classe 1 (orange) ou en classe 2 (bleu).

Un arbre de décision se rapproche d'une fonction linéaire en utilisant une fonction d'étape.

Cela est dû au type de règle de validation et de partitionnement utilisé par les arbres de décision. Ils fonctionnent tous selon un modèle  attribute < thresholdqui se traduira par des hyperplans parallèles aux axes . Dans l'espace 2D, les rectangles sont "coupés". En 3D, ce seraient des cuboïdes et ainsi de suite. De plus, l'arbre de décision commence à modéliser le bruit dans les données lorsqu'il y a déjà 8 niveaux, c'est-à-dire qu'un surajustement se produit. Cependant, il ne trouve jamais une bonne approximation d'une fonction linéaire réelle. Pour vérifier cela, j'ai utilisé une répartition typique de 2 en 1 des données d'entraînement et de test et calculé la précision des arbres. Il est de 93,84%, 93,03%, 90,81% pour l' ensemble de test et 94,54%, 96,57%, 98,81% pour l' ensemble d'apprentissage(classés par profondeur d'arbre 4, 8, 16). Alors que la précision du test diminue , la précision de la formation augmente .

Une augmentation de l'efficacité de la formation et une diminution des résultats des tests est un signe de surentraînement.

Les arbres de décision résultants sont assez complexes pour une fonction aussi simple. Le plus simple de ceux-ci (profondeur 4) rendu avec scikit learn ressemble déjà à ceci:







Je vais vous débarrasser des arbres plus difficiles. Dans la section suivante, nous commencerons par résoudre ce problème en utilisant le package HDTree. HDTree permettra à l'utilisateur d' appliquer ses connaissances sur les données (tout comme les connaissances sur la séparation linéaire dans l'exemple). Cela vous permettra également de trouver des solutions alternatives au problème.

Application du package HDTree

Cette section vous présentera les bases de HDTree. Je vais essayer de parler de certaines parties de son API. N'hésitez pas à demander dans les commentaires ou à me contacter si vous avez des questions à ce sujet. Je me ferai un plaisir de répondre et, si nécessaire, de compléter l'article. L'installation de HDTree est un peu plus compliquée que pip install hdtree. Pardon. Vous avez d'abord besoin de Python 3.5 ou plus récent.

• Créez un répertoire vide et à l'intérieur un dossier nommé hdtree ( your_folder/hdtree)
• Clonez le référentiel dans le répertoire hdtree (pas dans un autre sous-répertoire).
• Installer les dépendances requises: numpy, pandas, graphviz, sklearn.
• Ajouter your_folderà PYTHONPATH. Cela inclura le répertoire dans le moteur d'importation Python. Vous pourrez l'utiliser comme un package Python classique.

Vous pouvez également ajouter hdtreeà site-packagesvotre dossier d' installation python. Je peux ajouter le fichier d'installation plus tard. Au moment de la rédaction, le code n'est pas disponible dans le référentiel pip. Tout le code qui génère les graphiques et la sortie ci-dessous (ainsi que précédemment montré) se trouve dans le référentiel et est directement publié ici . Résoudre un problème linéaire avec un arbre frère



Commençons tout de suite par le code:

from hdtree import HDTreeClassifier, SmallerThanSplit, EntropyMeasure
hdtree_linear = HDTreeClassifier(allowed_splits=[SmallerThanSplit.build()], # Split rule in form a < b
    information_measure=EntropyMeasure(), # Use Information Gain for the scores attribute_names=['x', 'y' ]) # give the
    attributes some interpretable names # standard sklearn-like interface hdtree_linear.fit(X_street_train,
    y_street_train) # create tree graph hdtree_linear.generate_dot_graph()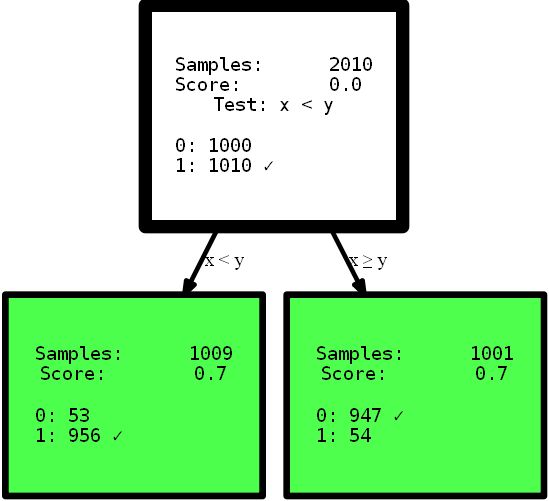 

Oui, l'arborescence qui en résulte n'a qu'un niveau de haut et offre la solution parfaite à ce problème. Ceci est un exemple artificiel pour montrer l'effet. Cependant, j'espère que cela rend les choses plus claires: avoir une vue intuitive des données, ou simplement fournir un arbre de décision avec différentes options pour diviser l'espace des fonctionnalités, ce qui peut offrir une solution plus simple et parfois même plus précise . Imaginez que vous deviez interpréter les règles des arbres présentés ici pour trouver des informations utiles. Quelle interprétation vous pouvez comprendre en premier et à laquelle vous faites le plus confiance? Une interprétation complexe utilisant des fonctions multi-étapes, ou un petit arbre précis? Je pense que la réponse est assez simple. Mais plongeons un peu plus dans le code lui-même. Lors de l'initialisation, la HDTreeClassifierchose la plus importante que vous devez fournir est allowed_splits. Vous fournissez ici une liste contenant les règles de partitionnement possibles que l'algorithme essaie pendant l'entraînement pour chaque nœud afin de trouver un bon partitionnement local des données. Dans ce cas, nous avons fourni exclusivement  SmallerThanSplit. Cette division fait exactement ce que vous voyez: elle prend deux attributs (essaie n'importe quelle combinaison) et divise les données en fonction du schéma a_i < a_j. Qui (pas trop au hasard) correspond aussi bien que possible à nos données.



Ce type de fractionnement est appelé fractionnement multivariéCela signifie que la séparation utilise plus d'une fonction pour prendre une décision. Ce n'est pas comme le partitionnement unidirectionnel utilisé dans la plupart des autres arbres, comme scikit-tree(voir ci-dessus pour plus de détails) qui prennent en compte exactement un attribut . Bien sûr, il a HDTreeégalement des options pour réaliser un "partitionnement normal" comme ceux des arbres scikit - la famille QuantileSplit. Je vais vous en montrer plus au fur et à mesure que l'article avance. Une autre chose inconnue que vous pourriez voir dans le code est l'hyperparamètre information_measure. Le paramètre représente une dimension utilisée pour évaluer la valeur d'un seul nœud ou d'un fractionnement complet (nœud parent avec ses nœuds enfants). L'option choisie est basée sur l'entropie [10]. Vous avez peut-être également entendu parler dele coefficient de Gini , qui serait une autre option valable. Bien entendu, vous pouvez fournir votre propre dimension en implémentant simplement l'interface appropriée. Si vous le souhaitez, implémentez un index gini , que vous pouvez utiliser dans l'arborescence sans rien réimplémenter . Copiez simplement EntropyMeasure()et adaptez-vous. Creusons plus profondément dans la catastrophe du Titanic . J'adore apprendre de mes propres exemples. Vous verrez maintenant quelques autres fonctions HDTree avec un exemple spécifique, pas sur les données générées.

Base de données

Nous travaillerons avec le célèbre jeu de données d'apprentissage automatique pour le cours Young Fighter: le jeu de données sur la catastrophe du Titanic. Il s'agit d'un ensemble assez simple, qui n'est pas trop volumineux, mais qui contient plusieurs types de données différents et des valeurs manquantes, bien que ce ne soit pas complètement trivial. De plus, il est compréhensible pour les humains et de nombreuses personnes ont déjà travaillé avec. Les données ressemblent à ceci:







Vous pouvez voir qu'il existe toutes sortes d'attributs. Numérique, catégorique, types entiers et même valeurs manquantes (regardez la colonne Cabin). Le défi consiste à prédire si un passager a survécu à la catastrophe du Titanic sur la base des informations disponibles sur les passagers. Vous pouvez trouver une description des attributs de valeur ici . En étudiant les didacticiels de ML et en appliquant cet ensemble de données, vous effectuez toutes sortes deprétraitement pour pouvoir travailler avec des modèles d'apprentissage automatique courants, par exemple, suppression des valeurs manquantes NaNen substituant des valeurs [12], suppression de lignes / colonnes, codage unitaire [13] données catégorielles (par exemple, Embarkedet / Sexou regroupement de données pour obtenir un ensemble de données valide qui accepte le modèle ML. Ce type de nettoyage n'est pas techniquement requis par HDTree. Vous pouvez servir les données telles quelles et le modèle les acceptera volontiers. Changez les données uniquement lors de la conception d'objets réels. J'ai tout simplifié pour commencer.

Entraîner le premier HDTree sur les données Titanic

Prenons simplement les données telles quelles et transmettons-les au modèle. Le code de base est similaire au code ci-dessus, cependant, dans cet exemple, beaucoup plus de fractionnements de données seront autorisés.

    hdtree_titanic = HDTreeClassifier(allowed_splits=[FixedValueSplit.build(), # e.g., Embarked = 'C'
    SingleCategorySplit.build(), # e.g., Embarked -> ['C', 'Q', 'S']
    TwentyQuantileRangeSplit.build(), # e.g., IN Quantile 3-5
    TwentyQuantileSplit.build()], # e.g., BELOW Quantile 7
    information_measure=EntropyMeasure(),
    attribute_names=col_names,
    max_levels=3) # restrict to grow to a max of 3 levels
    hdtree_titanic.fit(X_titanic_train.values, y_titanic_train.values)
    hdtree_titanic.generate_dot_graph()
    

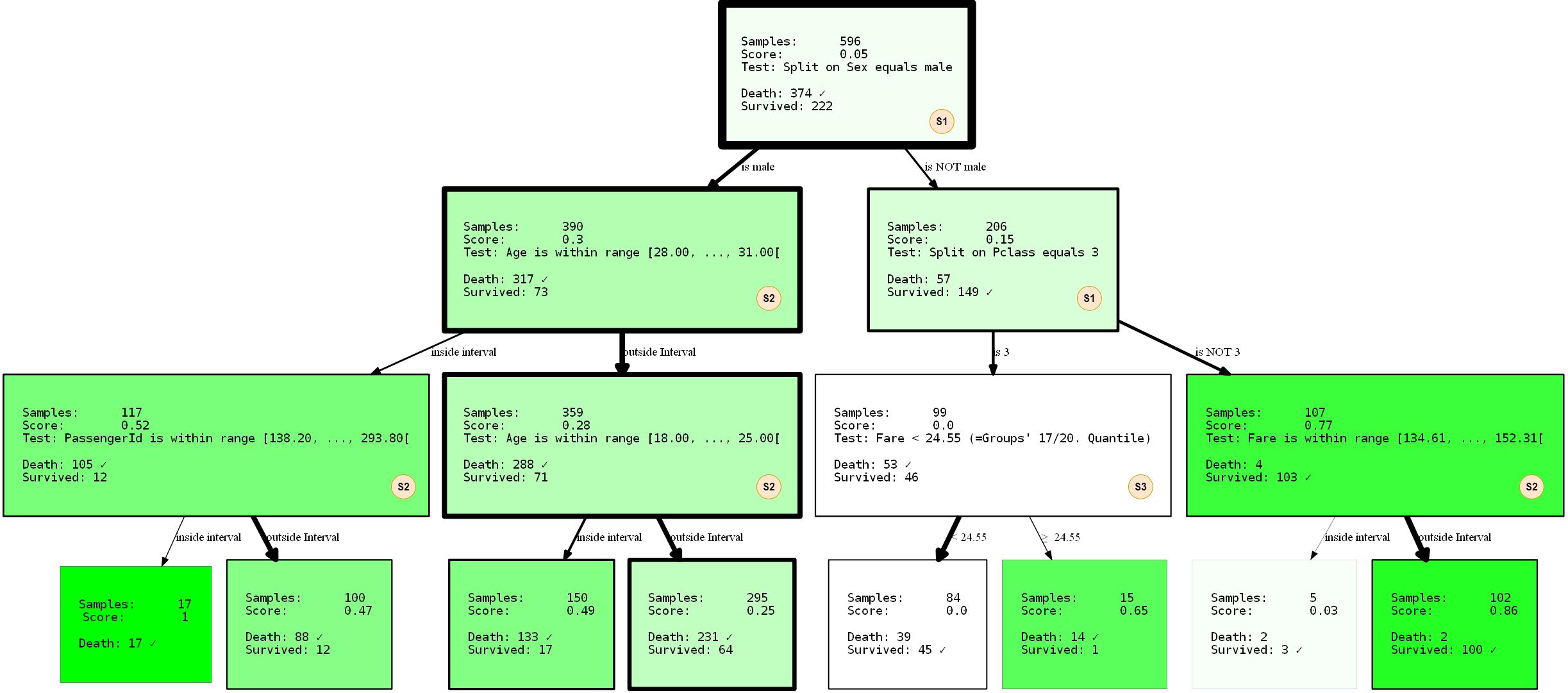
Regardons de plus près ce qui se passe. Nous avons créé un arbre de décision à trois niveaux, que nous avons choisi d'utiliser 3 des 4 SplitRules possibles . Ils sont marqués des lettres S1, S2, S3. Je vais expliquer brièvement ce qu'ils font.

• Le S1: FixedValueSplit. Cette division fonctionne avec des données catégorielles et choisit l'une des valeurs possibles. Les données sont ensuite divisées en une partie qui a cette valeur et une autre partie qui n'a pas de valeur définie. Par exemple, PClass = 1 et Pclass ≠ 1 .
• S2: () QuantileRangeSplit. . , . 1 5 . ( ) (measure_information). (i) (ii) — . .
• S3: (Vingt) QuantileSplit. Similaire à Split Range (S2), mais divise les données par seuil. C'est essentiellement ce que font les arbres de décision ordinaires, sauf qu'ils essaient généralement tous les seuils possibles au lieu d'un nombre fixe.

Vous avez peut-être remarqué que vous n'êtes SingleCategorySplitpas impliqué. Je prendrai une chance de clarifier de toute façon, car l'omission de cette division surviendra plus tard:

• S4: SingleCategorySplitfonctionnera de la même manière FixedValueSplit, mais créera un nœud enfant pour chaque valeur possible, par exemple: pour l'attribut PClass, ce sera 3 nœuds enfants (chacun pour la classe 1, la classe 2 et la classe 3 ). Notez qu'il FixedValueSplitest identique SingleValueSplits'il n'y a que deux catégories possibles.

Les divisions individuelles sont quelque peu «intelligentes» en ce qui concerne les types / valeurs de données qui «acceptent». Jusqu'à une certaine extension, ils savent dans quelles circonstances ils s'appliquent et ne s'appliquent pas. L'arbre a également été formé avec une répartition de 2 en 1 des données de formation et de test.La performance était de 80,37% de précision sur les données de formation et de 81,69 sur les données de test. Pas si mal.

Limiter les fractionnements

Supposons que vous n'êtes pas trop satisfait des solutions trouvées pour une raison quelconque. Peut-être que vous décidez que la toute première division en haut de l'arbre est trop triviale (division par attribut sex). HDTree résout le problème. La solution la plus simple serait d'empêcher FixedValueSplit(et, d'ailleurs, l'équivalent SingleCategorySplit) d'apparaître en haut. C'est assez simple. Modifiez l'initialisation des fractionnements comme ceci:

    - SNIP -
    ...allowed_splits=[FixedValueSplit.build_with_restrictions(min_level=1),
    SingleCategorySplit.build_with_restrictions(min_level=1),...],
    - SNIP -

Je vais présenter le HDTree résultant dans son intégralité, car nous pouvons observer le fractionnement manquant (S4) à l'intérieur de l'arbre nouvellement généré.







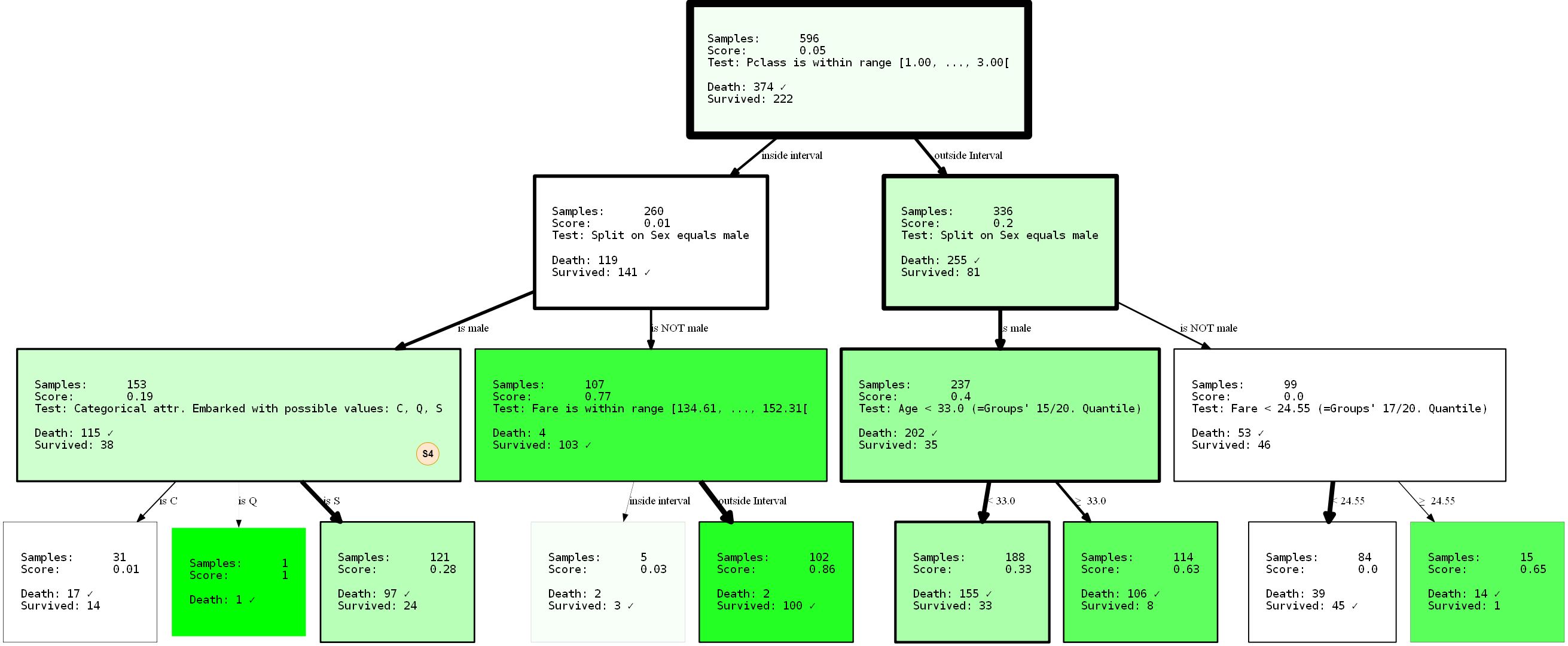
En empêchant le fractionnement d' sexapparaître à la racine grâce au paramètre  min_level=1(indice: bien sûr vous pouvez également fournir max_level), nous avons complètement restructuré l'arbre. Ses performances sont désormais de 80,37% et 81,69% (entraînement / test). Cela n'a pas du tout changé, même si nous avons pris la séparation supposée meilleure au niveau du nœud racine.

Comme les arbres de décision sont gourmands, ils ne trouveront que la _ meilleure partition locale pour chaque nœud, ce qui n'est pas nécessairement la _ meilleure _ option du tout. En fait, trouver une solution idéale à un problème d'arbre de décision est un problème NP-complet, comme cela a été démontré dans [15].

Donc, le mieux que nous puissions demander, ce sont les heuristiques. Revenons à l'exemple: remarquez que nous avons déjà une représentation non triviale des données? C'est trivial cependant. pour dire que les hommes n'auront que de faibles chances de survie, dans une moindre mesure, on peut en conclure qu'être une personne de premier ou de deuxième grade au PClassdépart de Cherbourg ( Embarked=C) peut augmenter vos chances de survie. Ou que faire si vous êtes un homme de  PClass 3moins de 33 ans, vos chances augmentent également? N'oubliez pas: les femmes et les enfants d'abord. C'est un bon exercice pour tirer ces conclusions vous-même en interprétant la visualisation. Ces conclusions n'ont été possibles qu'en raison de la limitation de l'arbre. Qui sait quoi d'autre peut être révélé en appliquant d'autres restrictions? Essayez-le!



Comme dernier exemple de ce genre, je veux vous montrer comment restreindre la partition à des attributs spécifiques. Cela s'applique non seulement pour empêcher l'apprentissage des arbres sur des corrélations indésirables ou des alternatives forcées , mais aussi pour restreindre l'espace de recherche. Cette approche peut réduire considérablement le temps d'exécution, en particulier lors de l'utilisation du partitionnement multivarié. Si vous revenez à l'exemple précédent, vous pouvez trouver un nœud qui recherche un attribut PassengerId. Nous pouvons ne pas vouloir le modéliser, car au moins il ne devrait pas contribuer à l'information sur la survie. La vérification de l'identité du passager peut être un signe de surentraînement. Changeons la situation avec un paramètre blacklist_attribute_indices.

    - SNIP -
    ...allowed_splits=[TwentyQuantileRangeSplit.build_with_restrictions(blacklist_attribute_indices=['PassengerId']),
    FixedValueSplit.build_with_restrictions(blacklist_attribute_indices=['Name Length']),
    ...],
    - SNIP -
    

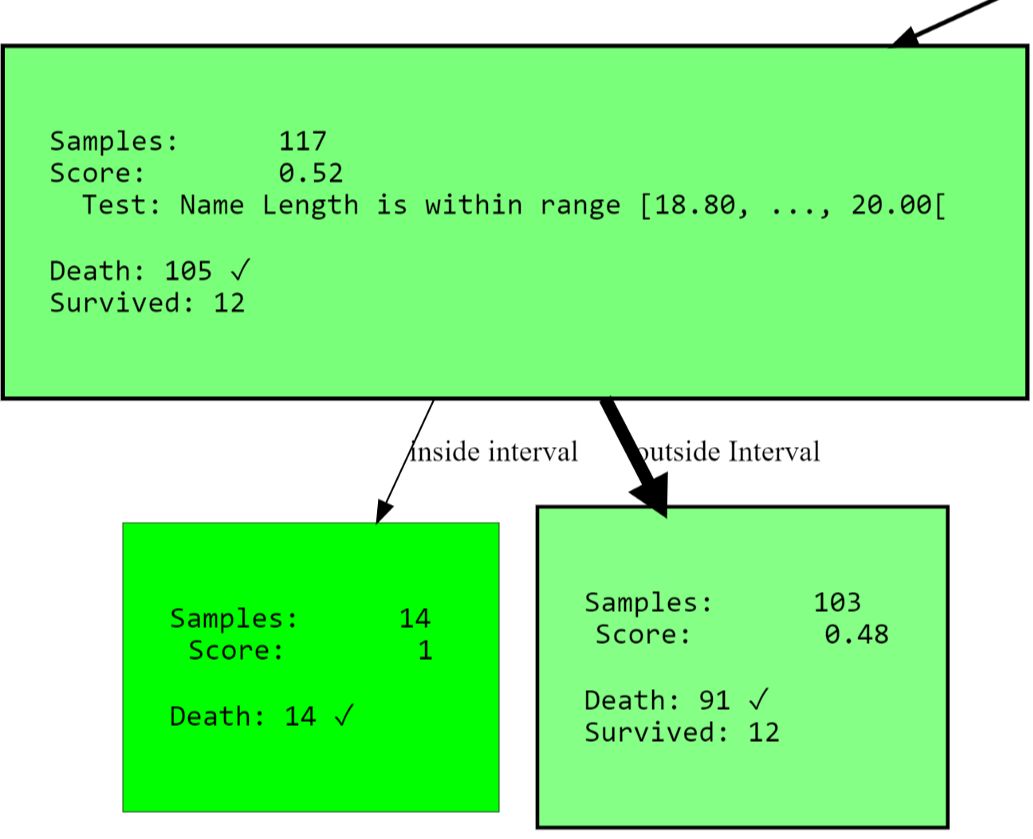
Vous vous demandez peut-être pourquoi name lengthcela apparaît. Sachez que les noms longs (doubles noms ou titres [nobles]) peuvent indiquer un riche passé, augmentant vos chances de survie.

Conseil supplémentaire: vous pouvez toujours ajouter SplitRuledeux fois la même chose  . Si vous souhaitez uniquement mettre sur liste noire un attribut pour certains niveaux HDTree, n'ajoutez simplement SplitRuleaucune limite de niveau.

Prédiction des points de données

Comme vous l'avez peut-être déjà remarqué, l'interface générique scikit-learn peut être utilisée pour la prédiction. Ce predict(), predict_proba()ainsi  score(). Mais vous pouvez aller plus loin. Il y en a explain_decision()un qui affichera la représentation textuelle de la solution.

print(hdtree_titanic_3.explain_decision(X_titanic_train[42]))

Ceci est supposé être la dernière modification apportée à l'arbre. Le code affichera ceci:

Query:
Query: 
 {'PassengerId': 273, 'Pclass': 2, 'Sex': 'female', 'Age': 41.0, 'SibSp': 0, 'Parch': 1, 'Fare': 19.5, 'Cabin': nan, 'Embarked': 'S', 'Name Length': 41}

Predicted sample as "Survived" because of: 
Explanation 1:
Step 1: Sex doesn't match value male
Step 2: Pclass doesn't match value 3
Step 3: Fare is OUTSIDE range [134.61, ..., 152.31[(19.50 is below range)
Step 4: Leaf. Vote for {'Survived'}
    

Cela fonctionne même pour les données manquantes. Définissons l'attribut index 2 ( Sex) sur absent (None):

    passenger_42 = X_titanic_train[42].copy()
    passenger_42[2] = None
    print(hdtree_titanic_3.explain_decision(passenger_42))
    

Query: 
 {'PassengerId': 273, 'Pclass': 2, 'Sex': None, 'Age': 41.0, 'SibSp': 0, 'Parch': 1, 'Fare': 19.5, 'Cabin': nan, 'Embarked': 'S', 'Name Length': 41}

Predicted sample as "Death" because of: 
Explanation 1:
Step 1: Sex has no value available
Step 2: Age is OUTSIDE range [28.00, ..., 31.00[(41.00 is above range)
Step 3: Age is OUTSIDE range [18.00, ..., 25.00[(41.00 is above range)
Step 4: Leaf. Vote for {'Death'}
---------------------------------
Explanation 2:
Step 1: Sex has no value available
Step 2: Pclass doesn't match value 3
Step 3: Fare is OUTSIDE range [134.61, ..., 152.31[(19.50 is below range)
Step 4: Leaf. Vote for {'Survived'}
---------------------------------
    

Cela affichera tous les chemins de décision (il y en a plus d'un, car sur certains nœuds, la décision ne peut pas être prise!). Le résultat final sera la classe la plus courante de toutes les feuilles.

... d'autres choses utiles

Vous pouvez continuer et obtenir l'arborescence sous forme de texte:

    Level 0, ROOT: Node having 596 samples and 2 children with split rule "Split on Sex equals male" (Split Score:
    0.251)
    -Level 1, Child #1: Node having 390 samples and 2 children with split rule "Age is within range [28.00, ..., 31.00["
    (Split Score: 0.342)
    --Level 2, Child #1: Node having 117 samples and 2 children with split rule "Name Length is within range [18.80,
    ..., 20.00[" (Split Score: 0.543)
    ---Level 3, Child #1: Node having 14 samples and no children with
    - SNIP -
    

Ou accédez à tous les nœuds propres (avec un score élevé):

    [str(node) for node in hdtree_titanic_3.get_clean_nodes(min_score=0.5)]
    

    ['Node having 117 samples and 2 children with split rule "Name Length is within range [18.80, ..., 20.00[" (Split
    Score: 0.543)',
    'Node having 14 samples and no children with split rule "no split rule" (Node Score: 1)',
    'Node having 15 samples and no children with split rule "no split rule" (Node Score: 0.647)',
    'Node having 107 samples and 2 children with split rule "Fare is within range [134.61, ..., 152.31[" (Split Score:
    0.822)',
    'Node having 102 samples and no children with split rule "no split rule" (Node Score: 0.861)']
    

Extension HDTree

La chose la plus importante que vous voudrez peut-être ajouter au système est la vôtre SplitRule. La règle de partitionnement peut vraiment faire tout ce qu'elle veut partitionner ... Implémentation SplitRulepar implémentation AbstractSplitRule. C'est un peu délicat car vous devez gérer vous-même l'ingestion de données, l'estimation des performances et tout cela. Pour ces raisons, il existe des mixins dans le package que vous pouvez ajouter à l'implémentation en fonction du type de fractionnement. Les mixins font le plus gros du travail pour vous.

Découvrez comment obtenir une profession de haut niveau à partir de zéro ou augmenter vos compétences et vos salaires en suivant les cours en ligne SkillFactory:

• Cours d'apprentissage automatique (12 semaines)
• Cours avancé "Machine Learning Pro + Deep Learning" (20 semaines)
• « Machine Learning Data Science» (20 )
• «Python -» (9 )

E

• Data Science (12 )
• - (8 )
• (9 )
• DevOps (12 )
• Java- (18 )
• JavaScript (12 )
• UX- (9 )
• Web- (7 )