👡 🆕 👩🏽‍🍳 Olympiade mathématique internationale 2020 (nous décidons dans les commentaires) 🤙🏼 👩🏼‍🎨 🙍🏻

Cette semaine (16-26 septembre) à Saint-Pétersbourg (pratiquement) a commencé la 61e Olympiade mathématique internationale , 622 écoliers de 114 pays y participent.

La première Olympiade de ce type a eu lieu en 1959 en Roumanie, et les représentants de sept pays seulement y ont pris part.

La Russie est représentée par une équipe de six lycéens.

Les écoliers disposent de 2 jours de 4,5 heures pour résoudre 6 problèmes. Pendant que les résultats sont évalués, je vous suggère d'essayer de résoudre les problèmes et d'en discuter dans les commentaires.

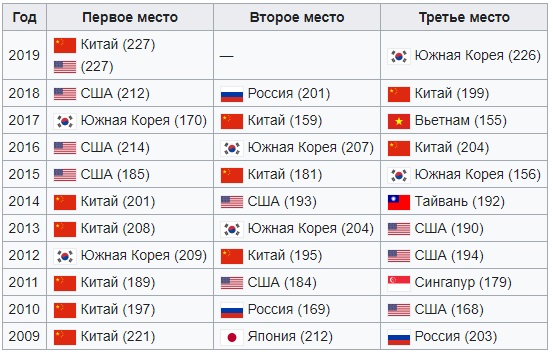
Résultats des années passées.

Problème 1

A l'intérieur du quadrilatère convexe ABCD, il y a un point P tel que les égalités

∠PAD: ∠PBA: ∠DPA = 1: 2: 3 = ∠CBP: ∠BAP: ∠BPC sont maintenues.

Montrer que les trois droites suivantes se coupent en un point: les bissectrices internes des angles ∠ADP et ∠PCB et le milieu perpendiculaire au segment AB.

Problème 2

Étant donné les nombres réels a, b, c, d tels que a> b> c> d> 0 et a + b + c + d = 1.

Montrer que

(a + 2b + 3c + 4d) a ^a b ^b c ^c d ^d <1.

Problème 3

Il y a 4n galets avec des masses 1, 2, 3, ..., 4n . Chacun des cailloux est peint dans l'une des n couleurs, et il y a 4 cailloux de chaque couleur.

Prouvez que les pierres peuvent être divisées en deux tas de poids total égal afin que chaque tas contienne deux pierres de chaque couleur.

Tâche 4

Un entier n> 1 est donné . Il y a n ² stations funiculaire sur la pente de la montagne à des hauteurs différentes. Chacune des deux sociétés de funiculaires A et B possède k ascenseurs. Chaque ascenseur effectue un transfert direct régulier d'une des stations à une autre station plus élevée. Les k transferts de la société A commencent à k stations différentes; ils se terminent également à k stations différentes; avec un transfert qui commence au-dessus et se termine au-dessus. Les mêmes conditions sont remplies pour l'entreprise B. On dira que deux stations sont connectéescompagnie de funiculaire, si vous pouvez vous rendre de la gare inférieure à la gare supérieure en utilisant un ou plusieurs transferts de cette société (les autres transferts entre gares sont interdits). Trouvez le plus petit k pour lequel il existe deux stations connectées par les deux sociétés.

Problème 5

Il existe n> 1 cartes, chacune contenant un entier positif.

Il s'est avéré que pour deux cartes quelconques, la moyenne arithmétique des nombres écrits dessus est égale à la moyenne géométrique des nombres écrits sur les cartes d'un certain ensemble constitué d'une ou plusieurs cartes. Pour quoi n s'ensuit-il que tous les nombres inscrits sur les cartes sont égaux?

Problème 6

Démontrez qu'il existe une constante positive c pour laquelle l'énoncé suivant est vrai:

Soit S un ensemble de n> 1 points du plan dans lequel la distance entre deux points quelconques est d'au moins 1. Il y a alors une ligne ℓ séparant l'ensemble S de telle sorte que la distance de tout les points S à ℓ sont au moins cn ^−1/3 .

(La droite ℓ sépare l' ensemble des points S si elle coupe un segment dont les extrémités appartiennent à S.)

Remarque. Des résultats plus faibles avec cn ^−1/3 remplacé par cn ^−α peuvent être estimés en fonction de la valeur de la constante α> 1/3 .

100 leçons de mathématiques par Alexey Savvateev

Olympiade mathématique internationale 2020 (nous décidons dans les commentaires)