Théorie des catégories pour les programmeurs. Sur les doigts

Bonjour chers collègues.







En développant notre intérêt constant pour la littérature académique sérieuse , pourrait-on dire , nous sommes arrivés à la théorie des catégories . Ce sujet dans la célèbre présentation de Bartosz Milevsky est déjà apparu sur Habré et il peut désormais se vanter de tels indicateurs: il est d'autant plus agréable que nous ayons réussi à trouver du matériel relativement frais (janvier 2020), qui sert d'introduction excellente et en même temps aussi brève que possible à la théorie des catégories. Nous espérons pouvoir vous intéresser à ce sujet.











Si vous et moi, cher lecteur, avons été confrontés à des problèmes similaires, alors vous avez été tourmenté une fois par la question "Qu'est-ce qu'une monade?!" Ensuite, vous avez googlé cette question, glissant furtivement dans le terrier du lapin des mathématiques abstraites , vous enchevêtrant dans les foncteurs , les monoïdes , les catégoriesjusqu'à ce qu'ils remarquent qu'ils avaient déjà oublié quelle question vous a amené ici. Cette expérience peut être assez écrasante si vous n'avez jamais vu de langages de programmation fonctionnels auparavant, mais ne vous inquiétez pas! J'ai étudié pour vous de nombreuses pages de mathématiques denses et regardé des heures de cours sur ce sujet. Donc, pour vous éviter ce besoin, je vais résumer le sujet ici et vous montrer également comment appliquer la théorie des catégories afin que vous puissiez penser (et écrire du code) dans un style fonctionnel dès maintenant.



Cet article est destiné à toute personne qui se considère comme un "débutant" dans le domaine de la programmation fonctionnelle et qui ne fait que commencer avec Scala, Haskell ou un autre langage similaire. Après avoir lu cet article, vous vous sentirez un peu plus en confiance pour interpréter les fondements de la théorie des catégories et identifier ses principes «sur le terrain». De plus, si vous vous êtes déjà essayé aux mathématiques théoriques, évitez de mentionner directement les concepts abordés ici. En règle générale, on peut en dire beaucoup plus sur chacun d'eux que ce qui est écrit ici, mais cet article sera suffisant pour un programmeur curieux.

Les bases

Alors, qu'est-ce qu'une catégorie exactement et comment se rapporte-t-elle à la programmation? Comme beaucoup de concepts utilisés en programmation, une catégorie est une chose très simple avec un nom sophistiqué. Ceci est juste un graphe orienté étiqueté avec quelques restrictions supplémentaires. Chacun des nœuds d'une catégorie est appelé un "objet" et chacun de ses bords est appelé un "morphisme".







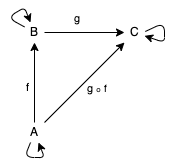
Comme vous l'avez peut-être deviné, tous les graphiques orientés ne sont pas une catégorie; pour qu'un graphique soit considéré comme une catégorie, certains critères supplémentaires doivent être remplis. Dans l'image suivante, nous notons que chaque objet a un morphisme qui pointe vers lui-même. Il s'agit d'un morphisme identique, et chaque objet doit avoir un tel que le graphique soit considéré comme une catégorie. Ensuite, notez que l'objet Aa un morphisme findiquantB, et, de même, l'objet Ba un morphisme gpointant vers C. Puisqu'il y a un chemin de Aà Bet de Bà C, il y a évidemment un chemin de Aà C, non? Ce sont les prochaines catégories d'exigences pour les morphismes, une composition nécessairement associative doit être effectuée, de sorte que pour un morphisme f: A = > B , et g: B = > Cil y a un morphisme h = g(f): A = > C.



Ces calculs peuvent déjà sembler un peu abstraits, alors regardons un exemple qui satisfait cette définition et est écrit en Scala.

trait Rock
trait Sand
trait Glass
def crush(rock: Rock): Sand
def heat(sand: Sand): Glass

Je pense que cet exemple rend la relation un peu plus facile. Effacer les pierres en sable est un morphisme qui transforme un objet rocken objet sand, tandis que fondre du verre à partir du sable est un morphisme qui transforme un objet sanden objet glass. Dans ce cas, la composition de ces relations ressemblera certainement à

val glass: Glass = heat(crush(rock))

Il existe également des fonctions d'identité (définies dans PredefScala), car pour tout objet, il n'est pas difficile d'écrire une fonction qui renvoie le même objet. Par conséquent, ce système est une catégorie, quoique assez simple.

Connaissance approfondie des catégories

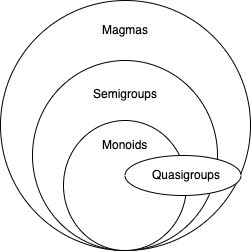
Nous allons maintenant approfondir un peu plus la terminologie de la théorie des catégories et commencer par une catégorie appelée magma. Si vous n'êtes pas encore trop familier avec ce concept de base, laissez-moi vous expliquer que le magma n'est qu'une opération binaire, c'est-à-dire une opération sur deux valeurs, à la suite de laquelle une nouvelle valeur est obtenue. Afin de ne pas entrer dans les détails, je ne donnerai pas ici la preuve que l'ensemble de toutes les opérations binaires est en fait une catégorie, mais pour ceux qui s'intéressent aux détails, je recommande de lire l'article suivant de Bartosz Milevsky. Toute l'arithmétique de l'addition à la multiplication appartient à des sous-catégories, unies par la catégorie magmatique (voir diagramme).



L'ordre d'héritage suivant s'applique ici:

• 1. Magma: toutes les opérations binaires
• 2. Demi-groupes: toutes les opérations binaires associatives
• o : .
• 3. : ,
• o : , (aka )

Donc, pour revenir à notre exemple précédent, l'addition et la multiplication sont des monoïdes car elles sont associatives (a + (b + c) = (a + b) + c)et ont un seul élément (ax 1 = 1 xa = a). Le dernier cercle de ce diagramme contient des quasigroupes pour lesquels des principes d'incorporation différents peuvent s'appliquer à ceux des semi-groupes ou des monoïdes. Les quasigroupes sont des opérations binaires réversibles. Il n'est pas si facile d'expliquer cette propriété, je vous renvoie donc à la série d'articles de Mark Siman consacrés à ce sujet. Une opération binaire est réversible lorsque pour toutes les valeurs aet bqu'il existe de telles valeurs xet yqui permettent la conversion aenb... Je sais que cela semble délicat. Pour être clair, regardons l'exemple suivant de soustraction:

val x = a - b
val y = a + b
assert(a - x == b)
assert(y - a == b)

Attention: il yne participe pas à la soustraction en tant que tel, mais l'exemple compte toujours. Les objets d'une catégorie sont abstraits et peuvent être presque n'importe quoi; dans ce cas, il est important que pour tout aet bqui peut être généré, ces déclarations restent vraies.

Types en contexte

Quelle que soit votre discipline particulière, le sujet des types doit être clair pour quiconque comprend la signification des types de données en programmation. Entier, booléen, virgule flottante, etc. sont tous des types, mais comment décririez-vous le type platonicien idéal dans les mots? Dans son livre Category Theory for Programmers, qui s'est transformé en une série d'articles de blog, Milevsky décrit les types simplement comme des «ensembles de valeurs». Par exemple, un booléen est un ensemble fini contenant les valeurs «vrai» et «faux» (faux). Un caractère (char) est un ensemble fini de tous les caractères numériques, et une chaîne (chaîne) est un ensemble infini de caractères.



Le problème est qu'en théorie des catégories, nous avons tendance à nous éloigner des ensembles et à penser en termes d'objets et de morphismes. Mais le fait que les types soient simplement des ensembles est inévitable. Heureusement, il y a une place dans la théorie des catégories pour ces ensembles, puisque nos objets sont des abstractions et peuvent représenter n'importe quoi. Par conséquent, nous avons le droit de dire que nos objets sont des ensembles, et de considérer en outre nos programmes Scala comme des catégories, où les types sont des objets et les fonctions sont des morphismes. Cela peut sembler douloureusement évident pour beaucoup; après tout, dans Scala, nous sommes habitués à traiter des objets, mais cela vaut la peine de le souligner explicitement.



Si vous avez travaillé avec un langage orienté objet tel que Java, vous êtes probablement familier avec le concept de types génériques. Ce sont des choses commeLinkedListou, dans le cas de Scala, Option[T]où Treprésente le type de données sous-jacent stocké dans une structure. Et si nous voulions créer un mappage d'un type à un autre afin que la structure du premier type soit préservée? Bienvenue dans le monde des foncteurs, définis comme des mappages entre catégories pour maintenir la structure. En programmation, vous devez généralement travailler avec une sous-catégorie de foncteurs, appelés endofoncteurs, qui aident à mapper une catégorie à elle-même. Donc je vais juste dire que quand je parle de foncteurs, je veux dire les endofoncteurs.



À titre d'exemple de foncteur, regardons le type Scala Option[T]en conjonction avec notre exemple précédent, qui mentionnait la pierre, le sable et le verre:

val rockOpt: Option[Rock] = Some(rock)

Ci-dessus, nous avons le type Rocktel que nous l'avons défini précédemment, mais enveloppé dans Option. Il s'agit d'un type générique (et plus d'informations ci-dessous), nous indiquant qu'un objet est soit une entité spécifique que nous recherchons, soit avec Nonelaquelle il peut être comparé nulldans d'autres langues.



Si nous n'utilisions pas de foncteurs, alors nous pourrions imaginer comment nous appliquons une fonction crush()à Rock, ce qui nécessiterait de recourir à un opérateur if pour gérer la situation dans laquelle elle se Optiontrouve None.

var sandOpt: Option[Sand] = None
if(rockOpt != None) {
  sandOpt = Some(crush(rockOpt.get))
}

Nous pourrions dire que c'est une dérive, mais veuillez ne pas utiliser var - un tel code est mauvais dans Scala pour plusieurs raisons. Encore une fois, revenons au sujet: en Java ou C #, ce ne serait pas un problème. Vous vérifiez si votre valeur est du type que vous vous attendiez à voir et faites ce que vous voulez avec. Mais avec la puissance des foncteurs, tout peut être fait un peu plus élégamment avec la fonction map():

val sandOpt: Option[Sand] = rockOpt.map(crush)

Boom, une ligne et vous avez terminé. Il serait possible de mettre le premier exemple sur une seule ligne, en utilisant l'opérateur ternaire ou quelque chose de similaire, mais vous n'auriez pas réussi si succinctement. Cet exemple est vraiment merveilleux dans sa simplicité. Voici ce qui se passe ici: il map()prend une fonction et mappe cette fonction (au sens mathématique) sur elle-même. La structure est Optionpréservée, mais maintenant elle contient soit Sand, soit None, au lieu de Rockou None. Cela peut être illustré quelque chose comme ceci:







Remarquez à quel point tout s'aligne magnifiquement, chaque objet et morphisme sont préservés dans les deux systèmes. Par conséquent, le morphisme au centre est un foncteur représentant une cartographie de Tà Option[T].

Ensemble

Maintenant, nous pouvons enfin revenir à la question initiale «qu'est-ce qu'une monade»? Il y a une réponse sur laquelle vous pouvez tomber aveuglément si vous essayez simplement de la rechercher sur Google, et cela ressemble à ceci: une monade est juste un monoïde dans la catégorie des endofoncteurs, qui est souvent suivie d'une remarque très sarcastique, "quel est le problème?" En règle générale, de cette manière, ils essaient de montrer en plaisantant à quel point tout est difficile dans ce sujet, mais en fait, tout n'est pas si effrayant - après tout, nous avons déjà compris ce que signifie cette phrase. Reprenons étape par étape.



Premièrement, nous savons que les monoïdes sont des opérations binaires associatives, chacune contenant un élément neutre (unique). Deuxièmement, nous savons que les endofoncteurs vous permettent de mapper une catégorie à elle-même, tout en conservant la structure. Ainsi, une monade est juste une sorte de type wrapper (comme dans l'exemple de type générique ci-dessus) qui maintient une méthode pour accepter une fonction et la mapper sur elle-même. List- c'est une monade, Option(comme celle que nous avons considérée ci-dessus) est une monade, et quelqu'un peut même vous le dire et Futurec'est aussi une monade. Exemple:

val l: List[Int] = List(1, 2, 3)
def f(i: Int) = List(i, i*2, i*3)
println(l.flatMap(f)) // : List(1, 2, 3, 2, 4, 6, 3, 6, 9)

C'est trompeusement simple, n'est-ce pas? À tout le moins, il devrait y avoir le sentiment qu'il n'est pas difficile de tout saisir ici, même si à première vue, on ne sait pas tout à fait à quoi sert un tel concept.