
Aujourd'hui, nous analyserons le discours de James Wootton d'IBM Quantum à la conférence FDG 2020. Nous parlerons de l'informatique quantique - une technologie potentiellement prometteuse, pour laquelle, cependant, il y a peu d'applications au stade actuel de développement. Et pourtant, l'un d'eux a été trouvé dans la génération procédurale.
Parlons plus en détail de la manière de l'implémenter sur les qubits, et donnons également les codes du programme.

Commençons par ce que sont les ordinateurs quantiques et leur utilité potentielle. N'entrons pas dans les détails techniques. Juste pour mentionner que les ordinateurs quantiques sont un modèle de calcul complètement différent des ordinateurs numériques et analogiques. Ils n'accélèrent pas seulement les logiciels conventionnels avec des quanta. Au lieu de cela, ils nécessitent une approche complètement différente de la mise en œuvre des programmes, ainsi que du matériel différent pour les exécuter.

L'informatique quantique pourra un jour effectuer certaines tâches beaucoup plus efficacement que l'informatique numérique ou analogique. Cela nous permettra de traiter des problèmes actuellement impossibles à résoudre. Après des décennies de recherche, de nombreux algorithmes quantiques ont été identifiés qui démontrent le plus efficacement ces avantages par rapport à un certain nombre d'applications possibles - y compris dans le domaine de la génération procédurale. Il s'agit notamment des problèmes d'optimisation, de la satisfaction des contraintes, de l'analyse graphique, etc.
Construire des ordinateurs capables d'effectuer de l'informatique quantique est une tâche ardue en soi, et se prépare depuis des années. L'un des paramètres importants pour décrire un dispositif quantique est le nombre de qubits. En fait, ce sont les mêmes bits, mais implémentés de manière quantique - et ont donc plus d'états que les 0 et 1. habituels. Dans le contexte de la physique quantique, nous pouvons écrire les valeurs des bits en utilisant une paire de vecteurs orthogonaux: | 0⟩ et | 1⟩. Dans le cas des qubits, la description des états sera complétée par des amplitudes complexes c 0 et c 1 , qui satisfont à la condition: | c 0 | 2 + | c 1 | 2= 1, grâce auquel un plus grand nombre d'états du qubit c 0 | 0⟩ + c 1 | 1⟩ est obtenu.

Nous avons besoin de plusieurs milliers de qubits pour exécuter des algorithmes phares, ce que nous n'aurons pas dans les prochaines années.
Actuellement, nous ne disposons pas de plusieurs milliers de qubits ni même d'un millier. Pour être honnête, nous n'avons même pas cent qubits. Le plus gros appareil actuellement disponible pour nous a 65 qubits. Bien que cela ne soit pas suffisant pour exécuter les algorithmes les plus intéressants et les plus efficaces que nous connaissons, même ce nombre de qubits peut fournir des résultats qui ne sont pas attendus des ordinateurs conventionnels. Cela est démontré par la complexité de l'émulation de tels appareils, pour lesquels vous devrez louer le plus grand supercalculateur du monde.
Le matériel quantique peut donc nous offrir des réponses uniques, mais au cours des dernières décennies, nous n'avons pas appris à poser les bonnes questions. Par conséquent, l'objectif principal de nos recherches actuelles est d'essayer de trouver le plus tôt possible comment faire quelque chose d'utile avec ces machines.

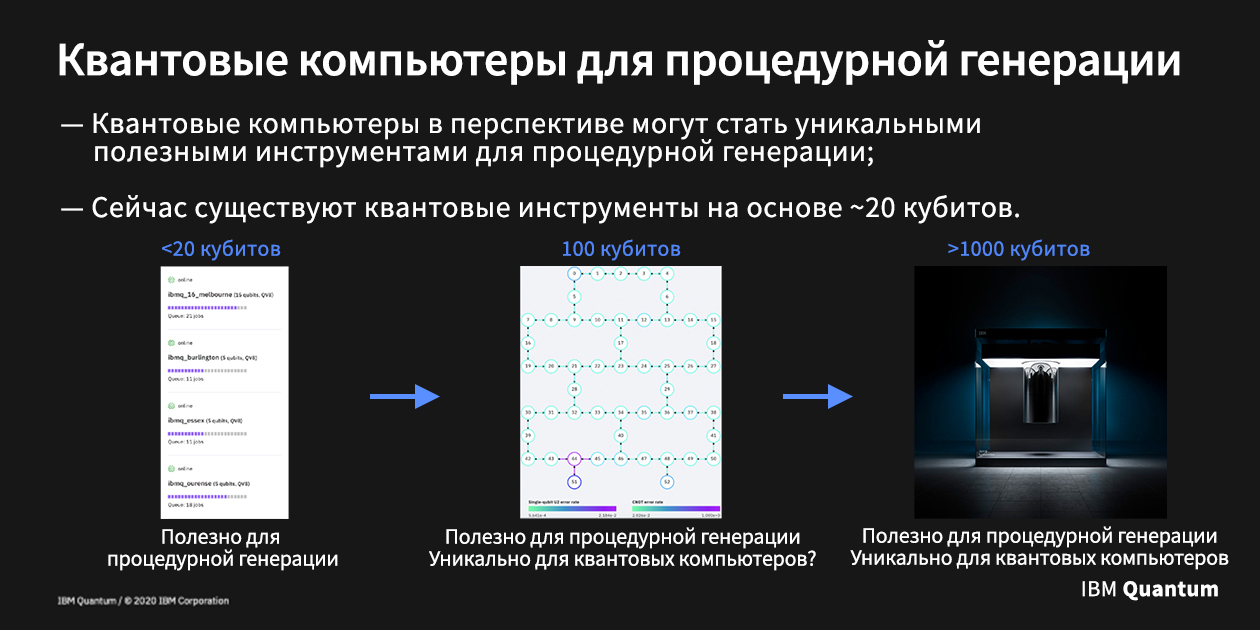
Il existe également des appareils de puissance plus modeste, composés d'environ 20 qubits. Et des programmes quantiques impliquant jusqu'à 15 qubits ont même été mis à disposition gratuitement par IBM. En outre, ils ont créé un logiciel d'émulation pour aider à la conception et aux tests de programmes quantiques. Et bien que l'émulation de plus de 50 qubits soit une tâche de calcul décourageante, même votre ordinateur portable peut gérer l'émulation d'environ 20 qubits sans aucun problème.
Tous les facteurs réunis font de 20 qubits un jalon. Que nous utilisions du matériel quantique réel ou son émulation, exécuter un logiciel quantique de ce niveau n'est pas trop difficile.

Alors qu'est-ce que tout cela signifie pour la génération procédurale? Cela dépend de laquelle des trois époques vous ciblez: celle d'aujourd'hui, prête à ne fournir que des dizaines de qubits; dans un proche avenir, lorsque les appareils auront des centaines de qubits; ou dans un futur lointain, lorsque plus de mille qubits seront disponibles pour nous.
Si nous parlons d'aujourd'hui, les logiciels quantiques, focalisés sur la puissance de seulement 20 qubits, ne peuvent toujours rien faire d'unique. Le fait même que nous puissions l'exécuter sur un émulateur signifie que vous n'avez même pas besoin de matériel quantique. Mais les programmes quantiques peuvent-ils encore faire quelque chose d'utile? Pouvons-nous écrire un programme quantique de 20 qubits qui donnera des résultats utiles au véritable utilisateur final?
Si nous pouvons obtenir des résultats vraiment utiles avec 20 qubits, cet effet ne fera que se multiplier avec le temps et plus de puissance de calcul. L'ère moyenne sera celle de la recherche sur des méthodes de plus en plus complexes de calcul quantique, y compris efficaces pour la génération procédurale. Nous allons passer à la création d'outils auxquels nous n'aurions probablement pas pensé si nous n'avions pas pensé en termes de quanta.
Mais n'allons pas trop vite. La première étape vers l'ère de l'utilité en expansion est de prouver que même un logiciel quantique de 20 qubits peut être utile. C'est ce que nous allons faire.
Il est maintenant temps de clarifier certains détails.
La génération procédurale signifie que nous devons générer quelque chose. Mais quoi?
La génération de terrain est la plus évidente, alors commençons par cela.
Le bruit Perlin est un outil omniprésent pour la génération procédurale de terrain. Mais il existe une autre méthode, beaucoup moins compliquée, pour la créer: utiliser un ensemble de points aléatoires avec leur flou ultérieur. La mise en œuvre de quelque chose comme celui-ci nous a semblé un objectif plus réalisable pour la première étape, nous allons donc le prendre comme base.
Commençons par développer un moyen d'encoder les altitudes sous la forme de circuits quantiques, qui sont des éléments fondamentaux du logiciel quantique. Ils ressemblent quelque peu aux modèles de circuits booléens pour l'informatique numérique. Les Qubits sont essentiellement les mêmes bits qui subissent des modifications différentes au fur et à mesure des calculs.

Nous travaillerons avec des images en noir et blanc, où la luminosité d'un pixel peut avoir une valeur de 0 à 1. De la même manière, elles peuvent être confondues avec des cartes de hauteur. Une fois que nous avons appris à encoder ces altitudes sous forme de schémas, nous pouvons les gérer. L'encodage utilisé vise à compresser le plus de points possible en le moins de qubits possible. Cette méthode ne laisse pas beaucoup de flexibilité pour offrir un contrôle pratique et flexible. Dans le même temps, presque tout changement dans le circuit provoquera des effets d'interférence.
Nous utilisons principalement des opérations qui peuvent être considérées comme des formes partielles de la porte NOT. Lorsqu'il est appliqué aux bits normaux, NE changez PAS la valeur de 0 à 1 et vice versa. À l'aide de portes quantiques, nous pouvons paramétrer cet élément pour effectuer une opération qui peut faire la moitié de NOT, ou un quart, ou toute autre partie fractionnaire qui peut être représentée par un ensemble de 2 n amplitudes de n qubits.
La fonction ci-dessous convertit l'image d'origine en un circuit quantique:
def height2circuit(height):
#
L = max(max(height))+1
#
grid = make_grid(L)
#
n = 2*int(np.ceil(np.log(L)/np.log(2)))
#
state = [0]*(2**n)
#
H = 0
for bit string in grid:
(x,y) = grid[bit string]
if (x,y) in height:
h = height[x,y]
state[ int(bit string,2) ] = np.sqrt( h )
H += h
#
for j,amp in enumerate(state):
state[ j ] = amp/np.sqrt(H)
#
qc = QuantumCircuit(n,n)
qc.initialize(state,range(n))
# Qiskit
# qc.initialize( state, qc.qregs[0])
return qcEnsuite, nous devons faire le processus inverse - transformer le circuit quantique en une image:
def circuit2height(qc):
#
n = qc.num_qubits
grid = make_grid(int(2**(n/2)))
#
ket = qi.Statevector(qc.data[0][0].params)
qc.data.pop(0)
#
ket = ket.evolve(qc)
#
p = ket.probabilities_dict()
#
max_h = max( p.values() )
#
height = {}
for bit string in p:
if bit string in grid:
height[grid[bit string]] = p[bit string]/max_h
return heightSi nous appliquons cette opération à tous les qubits, nous pouvons voir comment la heightmap change à mesure que la fraction augmente. Vous obtiendrez quelque chose comme un effet de flou. Des effets d'interférence se produiront alors, créant un motif qui ne peut pas être obtenu avec un simple flou.
Dans l'exemple ci-dessus en (a), nous commençons par une paire de points apparemment arbitraires. Peu à peu, ils subissent un flou, après quoi des effets d'interférence se superposent. Cela conduit à l'apparition d'un motif - dans notre cas, comme un damier sur (f). Ce résultat particulier a un lien clair avec les deux pixels avec lesquels nous avons commencé. Si vous prenez d'autres données comme point de départ, le résultat sera également complètement différent.
Quantum Blur a été développé et testé sur plusieurs game jams. Il est principalement utilisé pour générer des textures et des cartes de niveau.

Après avoir généré ces cartes, nous les utilisons pour l'analogue quantique du bruit haute fréquence de Perlin.
Alors maintenant, nous créons le profil principal - par exemple, les îles - d'une autre manière - comme dans © dans notre exemple. Ensuite, nous avons besoin d'un ensemble initial de pixels comme en (a). Nous le brouillons quantiques pour générer un motif comme (b). Après cela, nous l'appliquons au profil principal pour créer le paysage final.
Vous pouvez voir un exemple 2D ici, ainsi que le rendu 3D qui a été utilisé dans le jeu du didacticiel IBM QiskitBlocks. Des détails tels que des informations sur le type d'herbe et le placement des arbres dans le rendu 3D ont également été développés à l'aide d'opérations quantiques.

Étant donné que les images RVB sont généralement trois heightmaps alignées ensemble, nous pouvons également manipuler ces images. De cette façon, il est facile de créer des images étranges en utilisant la superposition. Plus difficile, mais plus efficace - encoder une paire d'images et créer un effet de téléportation entre elles.
La téléportation quantique transfère les informations entre les qubits. Nous prenons donc deux registres qubits de même taille et changeons simplement leurs états. Utilisons cette opération pour créer une animation de transition.

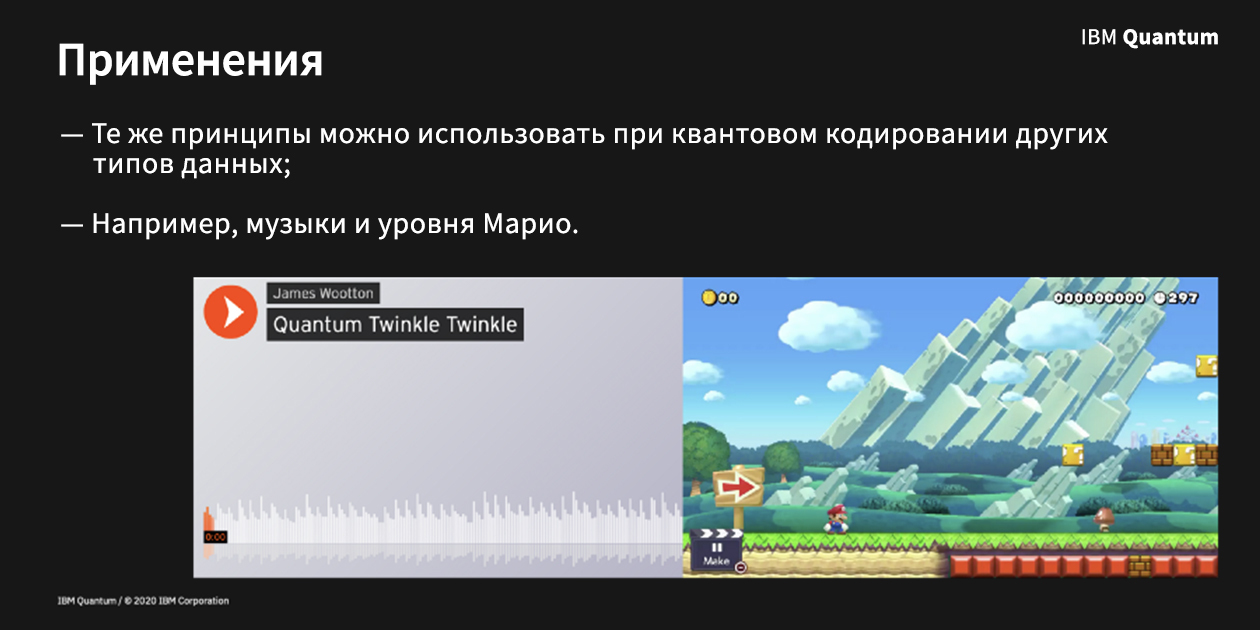
Une idée de codage similaire peut également être utilisée pour d'autres formes de données. Wootton a essayé de l'utiliser dans la musique:
et le niveau de Mario:
Voici deux autres exemples qui sont importants pour nous. L'un d'eux est un studio de jeux utilisant cette méthode pour la génération procédurale dans un futur jeu. Le projet a un cadre de science-fiction, et la méthode quantique lui apporte une véritable saveur de science.
L'artiste Libby Heaney a également utilisé certaines de ces idées comme point de départ pour son travail.
La nature quantique du calcul est mise en évidence dans ces deux cas: il est important pour l'utilisateur que les résultats proviennent du domaine quantique de l'espace de l'algorithme, et pas seulement de l'algèbre linéaire brillante.
La méthode décrite ici est plus appropriée pour l'émulation que pour le matériel quantique réel, mais cela changera bientôt. En fait, l'un des plus grands dispositifs quantiques d'IBM a également été utilisé pour la génération procédurale, bien que d'une manière complètement différente.
En attendant, vous pouvez essayer vous-même l'effet de flou quantique. Il est écrit en Python , mais il existe également un plugin pour Unity . Peut-être qu'ils vous seront utiles.
Lien vers l'article complet: ici .