Roger Penrose est le récipiendaire du prix Nobel de physique 2020 "pour sa découverte que la formation de trous noirs est une prédiction fiable de la relativité générale".
Aussi, le prix Nobel de physique a été décerné à Reinhard Henzel et Andrea Gez "pour la découverte d'un objet compact supermassif au centre de notre galaxie".
Roger Penrose est membre de la Royal Society of London. Il travaille dans divers domaines des mathématiques, de la relativité générale et de la théorie quantique. Penrose est l'auteur de théories liées à la conscience quantique, le saut quantique, la biologie quantique, et l'auteur du livre Fashion, Faith, Fantasy and the New Physics of the Universe, publié par Peter Publishing House.
Fashion, Faith, Fantasy and the New Physics of the Universe est basé sur trois conférences données par Penrose à l'Université de Princeton. L'auteur lui-même admet qu'en général la mode, la fantaisie et la foi ne dérangent pas du tout les personnes qui étudient sérieusement les principes fondamentaux de l'univers. Nous laisserons la foi aux églises, la mode aux défilés de mode, la fantaisie aux écrivains. Roger Penrose prouve sur 500 pages que ces mots romantiques peuvent être importants dans la recherche des fondements de l'univers.
Fantaisie
3.1. Le Big Bang et les univers Friedman
La fantaisie pourrait-elle jouer un rôle non illusoire dans nos tentatives de comprendre la réalité physique? Certes, le fantasme est tout le contraire de la science en tant que telle et n'a pas sa place dans un discours scientifique sérieux. Cependant, le sentiment demeure que cette question n'est pas aussi facile à écarter que cela puisse paraître - de nombreux processus naturels sembleront fantastiques, si nous partons des conclusions auxquelles une expérience scientifique rationnelle basée sur une recherche expérimentale fiable peut nous conduire. Comme nous l'avons vu, en particulier dans le chapitre précédent, le monde est vraiment organisé de la manière la plus fantastique si nous l'étudions au micro-niveau, où règnent les phénomènes quantiques. Un objet matériel spécifique peut se trouver à plusieurs endroits et, comme un vampire fabuleux (capable de se transformer d'une chauve-souris en humain et inversement quand il le souhaite),il peut afficher des propriétés corpusculaires ou ondulatoires comme si c'était son propre choix. De plus, son «comportement» obéit à des nombres mystérieux, qui contiennent la racine carrée imaginaire de -1.
De plus, à très grande échelle, des phénomènes sont à nouveau découverts, dont beaucoup peuvent sembler fantastiques - peut-être même plus frappants que toutes les découvertes de la fiction littéraire. Par exemple, des collisions sont parfois observées entre des galaxies entières, et il faut supposer qu'elles s'absorbent inévitablement (et nous corrigeons cela par les distorsions de l'espace-temps provoquées par les deux galaxies).
En effet, de telles distorsions de l'espace-temps peuvent parfois être observées même directement - par la courbure rugueuse d'images de galaxies très éloignées. De plus, les distorsions spatio-temporelles les plus extrêmes que nous connaissons peuvent conduire à l'émergence de trous noirs massifs dans l'espace: nous avons récemment réussi à observer comment deux de ces trous s'absorbent et en forment un encore plus grand [Abbott et al., 2016]. Il y a des trous noirs qui sont des millions ou des dizaines de milliers de millions de fois plus lourds que le Soleil, de sorte que ces trous pourraient facilement avaler des systèmes solaires entiers. Néanmoins, ces monstres sont très petits par rapport aux galaxies elles-mêmes, au centre desquelles ils se trouvent. Souvent, un tel trou noir trahit son existence, générant deux faisceaux collimatés de particules à haute énergie.Ces faisceaux sont expulsés du trou noir dans des directions opposées de la minuscule région centrale de la galaxie dans laquelle se trouve le trou; les particules volent à une vitesse pouvant atteindre 99,5% de la vitesse de la lumière [Tombesi et al., 2012; Piner, 2006]. Une fois, nous avons réussi à observer comment un tel faisceau a volé hors d'une galaxie et a visé une autre, comme s'il s'agissait d'une guerre intergalactique colossale.
À une échelle encore plus grande, des régions entières se trouvent remplies de quelque chose d'invisible qui imprègne l'espace. On a l'impression que cette substance totalement inconnue représente environ 84,5% de toute la matière de l'univers. En même temps, il y a autre chose qui atteint les limites les plus éloignées de l'Univers observé et, comme s'il le séparait dans des directions différentes à une vitesse croissante. Comme par désespoir, les scientifiques ont donné à ces deux entités des noms plutôt vagues - respectivement "matière noire" et "énergie noire". Ce sont la matière noire et l'énergie noire qui déterminent principalement la structure globale de l'univers connu. Le fait suivant semble encore plus alarmant: la cosmologie moderne prouve presque certainement que l'univers entier que nous connaissons est né d'une explosion géante,avant quoi il n'y avait rien du tout - voire pas du tout on peut parler de quelque chose "avant" l'émergence du continuum espace-temps, qui, comme nous le croyons, sous-tend toute réalité matérielle. Vraiment, un tel concept Big Bang est une idée fantastique!
Et voici; mais nous avons à notre disposition de plus en plus de preuves empiriques en faveur du fait qu'à l'aube de l'existence, notre univers était en effet incroyablement dense et en expansion rapide. Il contenait non seulement tout le contenu matériel du cosmos que nous connaissons, mais aussi tout l'espace-temps, sur fond duquel se joue maintenant l'existence de la réalité physique et qui, apparemment, s'étend à l'infini dans toutes les directions. Tout ce que nous savons semble être le résultat de ce Big Bang. Quelle est la preuve? Nous devons évaluer la crédibilité de cette idée et essayer de comprendre où elle peut nous mener.
Dans ce chapitre, nous discuterons quelques idées modernes sur l'origine de l'univers lui-même, et en particulier nous aborderons le problème suivant: dans quelle mesure est-il justifié de recourir à la fantaisie pour expliquer les faits empiriques. Ces dernières années, de nombreuses expériences nous ont en effet fourni de vastes quantités de données directement pertinentes pour comprendre les origines de l'univers. Des choses qui semblaient auparavant être une collection de spéculations pour la plupart non testées sont passées dans la catégorie de la science exacte. Les plus importants à mentionner sont les satellites COBE, lancé en 1989, WMAP, lancé en 2001, et l'Observatoire spatial. Une planche qui fonctionne depuis 2009. Les satellites susmentionnés ont progressivement étudié le fond de micro-ondes cosmique relique (voir section 3.4) de plus en plus en détail. Cependant, des problèmes non résolus demeurent,et à la recherche de réponses, certains spécialistes de la cosmologie théorique se sont enfoncés dans la jungle, ce qui est tout à fait approprié de l'appeler absolument fantastique.
Oui, dans une certaine mesure, la fantaisie est certainement justifiée, mais les théoriciens modernes ne se sont-ils pas précipités avec trop de zèle dans cette direction? Dans la section 4.3, je vais exprimer ma propre version plutôt non conventionnelle pour résoudre beaucoup de ces mystères. Les idées sur lesquelles ma réponse est impliquée peuvent également sembler folles à quelqu'un, et je vais décrire brièvement pourquoi elles devraient être prises au sérieux. Néanmoins, dans ce livre, je suis plus intéressé par les idées actuellement établies sur les premières étapes de l'évolution de notre merveilleux Univers, et je voudrais discuter de la plausibilité de certaines directions dans lesquelles certains cosmologues modernes mènent leurs recherches.
Pour commencer, nous avons la majestueuse théorie de la relativité générale d'Einstein, qui est connue pour être extrêmement précise dans la description de la structure de notre espace-temps courbe et du mouvement des corps célestes (voir les sections 1.1 et 1.7). En 1922 et 1924, après les premières tentatives d'Einstein pour appliquer cette théorie pour décrire la structure intégrale de l'Univers, le mathématicien russe Alexander Fridman a d'abord trouvé des solutions pour les équations de champ d'Einstein dans le contexte d'une distribution spatialement uniforme (homogène et isotrope) de la matière en expansion, et un liquide idéal était considéré comme un modèle approximatif de cette matière (solution de poussière) représentant la distribution moyenne masse-énergie des galaxies [Rindler, 2001; Wald, 1984; Hartle, 2003; Weinberg, 1972]. En effet, d'un point de vue empirique, il sembleque dans ce cas une assez bonne approximation générale de la distribution moyenne de la matière dans l'Univers existant est obtenue, et le tenseur d'énergie est dérivéT , dont Friedman avait besoin pour représenter la gravité dans l'équation d'Einstein G = 8π ע T + Λg (voir section 1.1). Une caractéristique des modèles de Friedman est que l'expansion commence par une singularité (maintenant ce moment s'appelle le Big Bang). Alors la courbure de l'espace-temps était infinie, et la densité masse-énergie de la source de matière T se précipiterait à l'infini si nous essayions de ramener le temps à cette singularité d'espace-temps.
(Étonnamment, le terme désormais couramment utilisé "Big Bang" était censé être péjoratif; il a été inventé par Fred Hoyle, un ardent partisan de la théorie alternative d'un univers stationnaire; voir la section 3.2.) Il a d'abord mentionné les mots "Big Bang" dans une interview à la radio de la BBC - une série de discours qu'il fabriqué en 1950. La section 3.10 mentionne ces entretiens dans un contexte différent; plus tard, un livre a été compilé sur leur base [Hoyle, 1950].
Pour l'instant, je supposerai conditionnellement que la très petite constante cosmologique d'Einstein Λ - c'est cette constante qui détermine l'accélération de l'expansion de l'Univers, mentionnée plus haut (voir aussi la section 1.1) - est égale à zéro. Ensuite, nous devons considérer seulement trois situations distinctes déterminées par la géométrie spatiale: la courbure de l'espace K peut être positive (K> 0), nulle (K = 0) ou négative (K <0). Dans les livres faisant autorité sur la cosmologie, il est habituel de normaliser la valeur de K, en l'amenant à l'une des trois valeurs suivantes: 1, 0, –1. Ici, l'histoire sera plus claire si l'on considère K comme un nombre réel caractérisant la courbure réelle de l'espace. Nous pouvons considérer K comme une quantité indiquant une telle courbure spatiale à un instant t spécialement sélectionné. Par exemple, vous pouvez accepterque t correspondra à l'époque de la dernière diffusion (voir section 3.4), lorsque le fond cosmique hyperfréquence s'est formé, mais le choix d'un moment spécifique n'est pas important dans ce cas. L'essentiel est que le signe de K ne changera pas avec le temps, par conséquent, une valeur positive, négative ou nulle de K caractérise le modèle dans son ensemble, quel que soit le «point de référence» choisi.
Cependant, il convient de noter que la valeur de K ne caractérise pas à elle seule pleinement la géométrie de l'espace-temps. Il existe également des versions "pliées" non standard de ces modèles, dont la géométrie spatiale est assez complexe, et dans certains exemples l'Univers peut être fini, même si K = 0 ou K <0. Certains scientifiques se sont intéressés à
de tels modèles (voir Levin [2012], Luminet et al., [2003], originellement Schwarzschild [1900]). Cependant, ces modèles ne sont pas importants pour nous ici; ce problème n'affecte pas de manière significative la plupart des arguments que je présente dans cette affaire. Si nous ne prenons pas en compte les difficultés topologiques, nous n'obtenons que trois types de géométrie homogène, qui (sur le plan) ont été très joliment représentées par l'artiste hollandais M.K. Escher (Fig.3.1; comparer également avec Fig.1.38 dans la section 1.15). L'image 3D a la même apparence.
Le moyen le plus simple de comprendre le cas est K = 0, car dans ce cas, la section spatiale sera un espace euclidien tridimensionnel ordinaire, bien que pour décrire l'Univers en expansion, nous ayons besoin de nombreuses sections successives: voir Fig. 3.2 b. (Cette expansion peut être comprise en termes de lignes temporelles divergentes qui correspondent aux lignes du monde des galaxies idéalisées décrites par ce modèle. Ce seront les lignes de temps, dont nous parlerons plus tard.) Les espaces tridimensionnels, qui sont des sections spatiales dans le cas de K> 0, sont un peu plus difficiles à représenter. puisqu'il s'agit de 3 sphères ( ), dont chacune en trois dimensions est similaire à la surface bidimensionnelle d'une sphère ordinaire (), et l'expansion de l'Univers s'exprime comme une augmentation du rayon de la sphère avec le temps (Fig. 3.2 a). Dans le cas d'une courbure négative (K <0), les espaces tridimensionnels ont une géométrie hyperbolique (aka géométrie de Lobachevsky). Cette géométrie peut être représentée avec précision en utilisant la représentation conforme (Beltrami - Poincaré), qui dans le cas bidimensionnel est décrite comme une région délimitée par un cercle S dans le plan euclidien, où les lignes droites sont représentées comme des arcs circulaires coupant le cercle englobant à angle droit (Fig. et Figure 1.38 de la section 1.15) (voir, en particulier, RQR, sections 2.4 à 2.6; Needham [1997]). La géométrie hyperbolique tridimensionnelle semble similaire, cependant, au lieu d'un cercle S, elle contient une sphère (2 sphères ordinaires), qui délimite une région (3 boules) dans l'espace tridimensionnel euclidien.
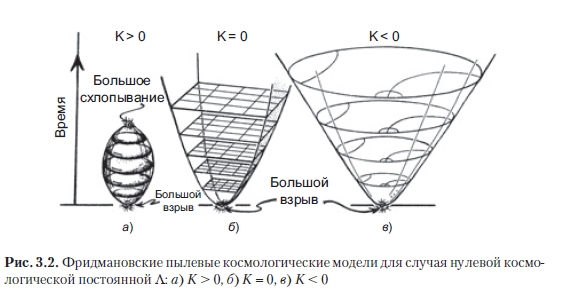
Le terme «conforme» utilisé dans ces modèles est utilisé car en géométrie hyperbolique, l'angle entre deux courbes lisses à leur point d'intersection sera le même que dans la géométrie euclidienne d'arrière-plan (par exemple, les angles aux extrémités des nageoires de poisson sur la Fig. 1.38a ou les ailes des démons de la figure 3.1c sont montrées sans distorsion, quelle que soit la distance du cercle englobant). Une autre formulation (grossière) du même principe est que les formes (mais pas les dimensions) des détails très fins dans de telles représentations sont toujours affichées sans distorsion (voir également la Figure A.39 de la Section A.10).
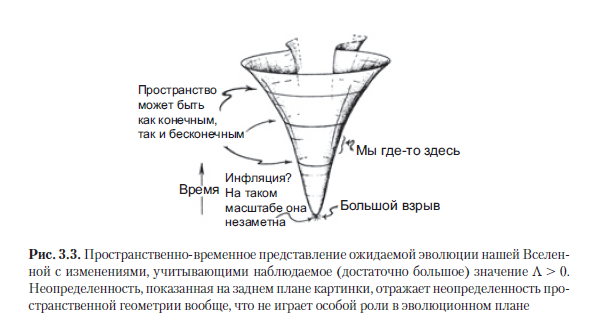
Comme indiqué précédemment, des preuves convaincantes ont déjà été trouvées que dans notre Univers la constante cosmologique Λ a une petite valeur positive, nous devons donc considérer les modèles de Friedmann correspondant à Λ> 0. En fait, aussi insignifiante que soit Λ, sa valeur est toujours suffisante est grand (en même temps, selon les équations d'Einstein, nous continuons à le considérer comme une constante) afin de surmonter l'effondrement et le «grand effondrement» représentés sur la Fig. 3.2 a. Au lieu de cela, avec les trois valeurs K possibles autorisées par les observations actuelles, l'univers devrait éventuellement s'étendre avec l'accélération. Avec une telle constante positive Λ, l'expansion de l'Univers se poursuivra indéfiniment et finira par devenir exponentielle (voir Figure A.1 dans la section A.1).Selon de tels calculs, nous imaginons l'histoire générale de l'Univers comme le montre la Fig. 3.3. L'arrière-plan est représenté de manière vague pour montrer que les observations permettent les trois variations de la courbure spatiale de K.
Les variantes du futur lointain dans tous ces modèles pour Λ> 0, même avec quelques irrégularités, sont très similaires et sont bien décrites par un modèle spatio-temporel spécifique, appelé espace de Sitter. Le tenseur T d'Einstein est simplement Λg . Ce modèle a été trouvé par Willem de Sitter (et indépendamment par Tullio Levi-Civita) en 1917 (voir [de Sitter, 1917a, b; Levi-Cività, 1917; Schrödinger, 1956]; PKR, p. 28.4). À l'heure actuelle, il est généralement admis que ce modèle se rapproche bien du futur lointain de notre Univers, lorsque le tenseur d'énergie est complètement déterminé par Λ, donc, dans un avenir extrêmement lointain, la situation G≈Λg se développera .
Bien entendu, nous supposons ici que les équations d'Einstein (G = 8π ע T + Λg)agira indéfiniment et la valeur de Λ, définie à notre époque, restera constante. La section 3.9 montrera que, selon les idées exotiques de la cosmologie inflationniste, le modèle de de Sitter aurait dû décrire l'Univers à un stade beaucoup plus précoce, immédiatement après le Big Bang, mais la valeur de Λ à ce moment-là aurait dû être colossalement plus élevée que l'actuelle. Ces questions deviendront importantes pour nous plus tard (voir les sections 3.7-3.9 et 4.3), mais pour l'instant nous ne nous attarderons pas sur elles en détail.
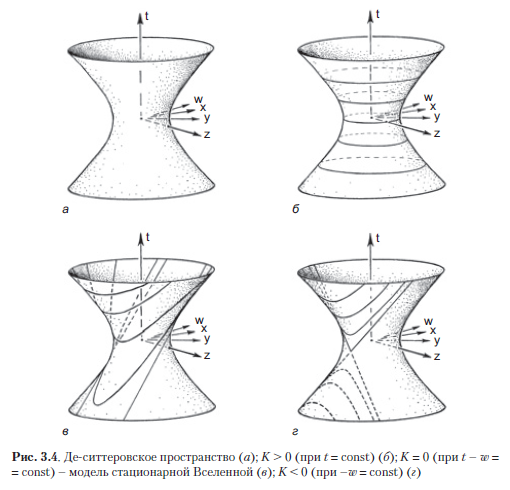
L'espace De Sitter est un espace-temps hautement symétrique qui peut être décrit comme une (pseudo-) sphère dans un espace de Minkowski à cinq dimensions (Fig. 3.4 a). Cette (pseudo-) sphère apparaît au point = –3 / Λ, obtenant une structure métrique locale à partir de l'espace de Minkowski à cinq dimensions englobant avec des coordonnées (t, w, x, y, z) (Ceux qui savent comment le standard les métriques sont écrites à l'aide de différentiels, on comprend que cette métrique de Minkowski en cinq dimensions prend la forme =.) L'espace De-Sitter répète complètement la symétrie de l'espace de Minkowski à quatre dimensions; dans les deux cas, nous avons un groupe de symétrie à 10 paramètres. Vous pouvez également rappeler l'espace hypothétique anti-de-Sitter discuté dans la section 1.15. Il est très étroitement lié à l'espace de Sitter et possède un groupe de symétrie du même ordre.
L'espace De Sitter est un modèle vide dans lequel le tenseur d'énergie Test zéro, il n'y a donc pas de galaxies (idéalisées) qui pourraient définir des lignes de temps, dont les sections spatiales tridimensionnelles orthogonales permettraient de définir des géométries tridimensionnelles spécifiques du «temps synchrone». En fait, un fait assez remarquable: il s'avère que de telles sections spatiales tridimensionnelles (avec un temps synchrone) peuvent être choisies dans l'espace de Sitter de trois manières fondamentalement différentes, de sorte que l'espace de Sitter peut être interprété comme un Univers s'étendant uniformément dans l'espace avec chacune des trois alternatives. types de courbure spatiale, selon la façon dont elle est coupée par ces sections tridimensionnelles correspondant au même temps cosmique: K> 0 (à t = const), K = 0 (à t - w = const) et K <0 ( à –w = const) (Fig. 3.4 b - d).Cela a été magnifiquement démontré par Erwin Schrödinger dans son livre Expanding Universes (1956). Un modèle antérieur d'un univers stationnaire, que nous discuterons dans la section 3.2, est décrit par l'espace de Sitter conformément à la section transversale K = 0 représentée sur la Fig. 3.4 c (et présenté de manière conforme à la Fig. 3.26 b de la section 3.5). La plupart des versions de la cosmologie inflationniste (que nous atteindrons dans la section 3.9) utilisent également une telle coupe K = 0, de sorte que l'inflation peut continuer de manière uniforme et exponentielle pendant un temps illimité.26 b dans la section 3.5). La plupart des versions de la cosmologie inflationniste (que nous aborderons dans la section 3.9) utilisent également une telle coupe K = 0, de sorte que l'inflation peut continuer de manière uniforme et exponentielle pendant une durée illimitée.26 b dans la section 3.5). La plupart des versions de la cosmologie inflationniste (que nous atteindrons dans la section 3.9) utilisent également une telle coupe K = 0, de sorte que l'inflation peut continuer de manière uniforme et exponentielle pendant une durée illimitée.
En fait, en ce qui concerne la structure à grande échelle de notre Univers réel, les observations modernes ne nous permettent pas de répondre sans équivoque à laquelle de ces variantes de géométrie spatiale la décrit le plus précisément. Cependant, quelle que soit la réponse finale, il ne semble pas maintenant que l'option K = 0 soit aussi proche de la vérité (à noter, surtout compte tenu des preuves apparemment convaincantes en faveur de K <0 qui sont apparues vers la fin du 20e siècle). En un sens, cette situation est extrêmement insatisfaisante d'un point de vue empirique; car si l'on peut seulement dire que la valeur de K est très proche de zéro, alors il y a encore la possibilité qu'une observation plus attentive (ou une théorie plus convaincante) montre par la suite queque notre Univers correspond plus précisément à une autre géométrie spatiale (c'est-à-dire sphérique ou hyperbolique). Donc, si à la fin il y a de bonnes preuves en faveur de K> 0, ce sera vraiment important d'un point de vue philosophique, car cela signifierait que les dimensions spatiales de l'univers sont finies. Cependant, à partir de maintenant, il est habituel de dire simplement ce qui suit: d'après les observations, K = 0. Cela peut être une très bonne approximation, mais en tout cas nous ne savons pas à quel point l'univers réel est proche de la véritable homogénéité spatiale et de l'isotropie, surtout compte tenu de certaines données contradictoires. obtenu en observant le fond cosmique des micro-ondes (par exemple, [Starkman et al., 2012; Gurzadyan et Penrose, 2013, 2016]).si à la fin il y a de bonnes preuves en faveur de K> 0, ce sera vraiment important d'un point de vue philosophique, car cela signifierait que les dimensions spatiales de l'univers sont finies. Cependant, à partir de maintenant, il est habituel de dire simplement ce qui suit: d'après les observations, K = 0. Cela peut être une très bonne approximation, mais en tout cas nous ne savons pas à quel point l'univers réel est proche de la véritable homogénéité spatiale et de l'isotropie, surtout compte tenu de certaines données contradictoires. obtenu en observant le fond cosmique des micro-ondes (par exemple, [Starkman et al., 2012; Gurzadyan et Penrose, 2013, 2016]).si à la fin il y a de bonnes preuves en faveur de K> 0, ce sera vraiment important d'un point de vue philosophique, car cela signifierait que les dimensions spatiales de l'univers sont finies. Cependant, à partir de maintenant, il est habituel de dire simplement ce qui suit: d'après les observations, K = 0. Cela peut être une très bonne approximation, mais en tout cas nous ne savons pas à quel point l'univers réel est proche de la véritable homogénéité spatiale et de l'isotropie, surtout compte tenu de certaines données contradictoires. obtenu en observant le fond cosmique des micro-ondes (par exemple, [Starkman et al., 2012; Gurzadyan et Penrose, 2013, 2016]).Cependant, à partir de maintenant, il est habituel de dire simplement ce qui suit: d'après les observations, K = 0. Cela peut être une très bonne approximation, mais en tout cas nous ne savons pas à quel point l'univers réel est proche de la véritable homogénéité spatiale et de l'isotropie, surtout compte tenu de certaines données contradictoires. obtenu en observant le fond cosmique des micro-ondes (par exemple, [Starkman et al., 2012; Gurzadyan et Penrose, 2013, 2016]).Cependant, à partir de maintenant, il est habituel de dire simplement ce qui suit: d'après les observations, K = 0. Cela peut être une très bonne approximation, mais en tout cas nous ne savons pas à quel point l'univers réel est proche de la véritable homogénéité spatiale et de l'isotropie, surtout compte tenu de certaines données contradictoires. obtenu en observant le fond cosmique des micro-ondes (par exemple, [Starkman et al., 2012; Gurzadyan et Penrose, 2013, 2016]).
Afin de construire une image de l'espace-temps complet selon les modèles de Friedmann et leurs généralisations, vous devez savoir comment les «dimensions» de notre géométrie spatiale vont évoluer au fil du temps, et dès le début. Dans les modèles cosmologiques standard, par exemple de Friedman, ou dans les modèles généralisés, brièvement appelés FLRU (Friedman - Lemaitre - Robertson - Walker), dans tous les modèles de cette classe générale les sections spatiales sont homogènes et isotropes et l'espace-temps total a la même symétrie que et les sections elles-mêmes. Ils ont une définition claire du temps cosmique t, qui décrit l'évolution d'un tel modèle universel. Ce temps cosmique commence à l'instant t = 0 (Big Bang) et est compté par des horloges idéalisées suivant les lignes du monde des galaxies idéalisées (Fig.3.5, ainsi que Fig.1.17 dans la section 1.7). Je ferai référence à ces lignes du monde comme des lignes de temps dans le modèle FLRU (dans les travaux cosmologiques, elles sont aussi parfois appelées lignes du monde des observateurs fondamentaux). Les chronologies sont des courbes géodésiques orthogonales aux sections spatiales, qui, à leur tour, sont des plans à 3 plans avec la même valeur t.
Le cas de l'espace de Sitter a une caractéristique importante: puisque, comme mentionné précédemment, l'espace est vide, c'est-à-dire que le tenseur d'énergie-impulsion T dans l'équation G = 8πT + Λg est égal à zéro, alors nous n'avons aucune ligne du monde associée à des corps matériels, ce qui a permis définirions-nous des lignes de temps ou, respectivement, la géométrie spatiale. Par conséquent, localement, nous avons le choix d'interpréter ce modèle de description de l'Univers: s'il correspond à K> 0, K = 0 ou K <0. Néanmoins, globalement, ces trois situations diffèrent, comme on peut le voir sur la Fig. 3.4 b - d: dans chacun de ces cas, le découpage capture une partie différente de l'espace de-Sitter intégral. Plus loin
Je partirai du fait que T n'est pas égal à zéro et fournit une densité d'énergie positive de la matière, ce qui permet de bien déterminer à la fois les lignes de temps et les 3 surfaces spatiales de temps constant pour chaque valeur de t, comme le montre la Fig. 3.2.
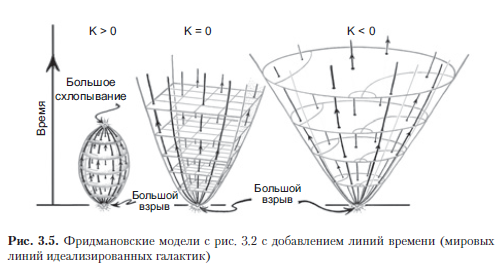
Dans le cas d'une courbure positive de l'espace (K> 0) dans l'Univers de Friedman standard rempli de poussière, on peut caractériser sa «taille» en utilisant le rayon R de sections spatiales à 3 sphères, et étudier cette taille en fonction de t. A Λ = 0, on retrouve la fonction R (t) décrivant la cycloïde dans le plan (R, t) (dans ce cas, la vitesse de la lumière est prise comme une unité: c = 1). Une cycloïde est une courbe avec une caractéristique géométrique simple: elle est décrite par un point d'un cercle roulant le long de l'axe t (Fig. 3.6 b). Notez que (après l'heure) la valeur de R atteint à nouveau zéro, comme dans le Big Bang, donc tout le modèle de l'Univers avec 0 <t < s'effondre à nouveau dans une singularité, et ce moment est souvent appelé un grand effondrement.
Dans les cas restants K <0 et K = 0 (avec zéro Λ), l'Univers s'étendra à l'infini et il n'y aura pas de grand effondrement. Dans le cas K <0, il existe un «rayon» similaire à R, mais pour K = 0, vous pouvez simplement choisir une paire arbitraire de lignes du monde de galaxies idéalisées et prendre comme R un segment les divisant dans l'espace. Dans le cas K = 0, le taux d'expansion tend asymptotiquement vers zéro, et dans le cas K <0 - vers une valeur positive.
Les observations modernes indiquent que Λ est très probablement positif et que sa valeur est suffisante pour jouer un rôle décisif dans le taux d'expansion de l'Univers, donc la valeur de K perd son importance pour cette dynamique, et l'Univers se décompose finalement en une expansion accélérée, comme le montre figure. 3.3.
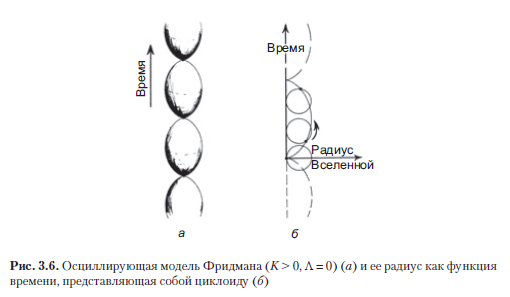
A l'aube de la cosmologie relativiste, un modèle avec une valeur K positive (et Λ = 0) était souvent appelé modèle oscillant (Fig. 3.6 a), puisque la courbe cycloïde se poursuivra indéfiniment si l'on laisse le "cerceau" faire plus d'un tour (courbe en pointillés sur la Fig. 3.6 b ). On peut supposer que le remplacement continu de sections de la cycloïde peut correspondre à des cycles successifs de l'histoire de l'Univers réel, où, sous l'influence d'une sorte de bouleversement, chaque effondrement que subit l'Univers est remplacé par un nouveau Big Bang. Une possibilité similaire se présente également à K = 0, et on peut supposer qu'à un stade antérieur, l'espace-temps a subi un effondrement, identique au renversement du temps au stade de l'expansion, et le grand effondrement de cette étape coïncide avec le Big Bang, que nous considérons comme le début de l'expansion actuelle de l'Univers.Encore une fois, vous devriez imaginer une sorte de rebond qui vous permet en quelque sorte de transformer l'implosion en une extension.
Cependant, pour qu'une telle image devienne physiquement plausible, il est nécessaire de présenter un schéma mathématique convaincant qui serait en accord avec les concepts et méthodes physiques modernes et dans lequel un tel rebond s'intégrerait. Par exemple, supposons que vous puissiez changer les équations d'état que Friedman a adoptées, avec lesquelles il a essayé de décrire la distribution générale de la matière dans ses galaxies «uniformément enduites». Friedman a utilisé un modèle approximatif parfois appelé un modèle de poussière; ce modèle ne prend en compte aucune interaction (à l'exception de la gravité) entre "éléments constitutifs" (ie "galaxies"), dont les lignes du monde sont des lignes de temps. Si nous changeons les équations d'état, cela peut affecter significativement les propriétés de R (t) près de t = 0. Une approximation encore plus précise,plutôt que la poussière de Friedman (dans la période immédiatement après le Big Bang), une telle équation d'état apparaît, qui a ensuite été utilisée par Richard Chase Tolman [1934], un spécialiste américain en physique mathématique et cosmologie. Dans les modèles FLRU de Tolman, l'équation d'état du rayonnement pur a été utilisée. On pense que c'est une bonne approximation de l'état de la matière aux premiers stades du développement de l'Univers, quand il faisait si chaud que chaque particule avait beaucoup plus d'énergie que l'équationqu'il se rapproche bien de l'état de la matière aux premiers stades du développement de l'Univers, quand il faisait si chaud que chaque particule avait significativement plus d'énergie que selon l'équationqu'il se rapproche bien de l'état de la matière aux premiers stades du développement de l'Univers, quand il faisait si chaud que chaque particule avait significativement plus d'énergie que selon l'équationpour la masse m même des particules les plus lourdes qui pourraient exister immédiatement après le Big Bang. Dans le schéma de Tolman pour le cas K> 0, la courbe R (t) n'est pas un arc de cycloïde, mais (avec une échelle correctement choisie de R et t) forme un demi-cercle (Fig. 3.7). Dans le cas du modèle poussières, il serait possible de justifier le passage de l'effondrement à l'explosion en recourant à une suite analytique (voir section A.10), qui permet en effet de passer d'un arc de la courbe cycloïde au suivant de manière aussi mathématique. Mais dans le modèle de Tolman avec rayonnement pur, la suite analytique compléterait simplement le demi-cercle et le transformerait en cercle, et cela n'a aucun sens si cette procédure nous intéresse pour décrire un rebond, c'est-à-dire qu'elle devrait permettre une continuation vers des valeurs négatives de t.
Pour que la nouvelle équation d'état décrive le mécanisme de rebond, il faut quelque chose de beaucoup plus radical que le rayonnement de Tolman. Dans ce cas, un point aussi grave mérite l'attention: si un rebond se produit à une transition non singulière, au cours de laquelle la douceur de l'espace-temps et la symétrie spatiale du modèle sont préservées, alors les lignes temporelles convergentes de la phase de compression peuvent se transformer en lignes temporelles divergentes de la phase d'expansion, passant par le goulot d'étranglement. «Cela combinerait ces deux phases. Si ce cou était lisse (non singulier), alors la transformation d'une telle convergence extrême des lignes de temps en une divergence extrême serait réalisable avec une incroyable courbure du cou, ce qui conduirait à une forte répulsion, et cela contredit grossièrement les conditions standard de l'énergie positive,qui est satisfaite par la matière classique ordinaire (voir les sections 1.11, 3.2 et 3.7; [Hawking et Penrose, 1970]).
On ne peut donc pas s'attendre à ce qu'une équation d'état classique raisonnable permette de décrire le rebond dans le contexte des modèles FLRU, et la question se pose inévitablement: les équations de la mécanique quantique ne nous aideraient-elles pas à avancer dans cette direction? Il faut tenir compte du fait qu'à proximité de la singularité FLRU classique, la courbure de l'espace-temps devient indéfiniment grande. Si nous essayions de décrire une telle courbure en fonction de son rayon, alors ce rayon (l'inverse de la courbure) serait proportionnellement petit. En continuant à adhérer aux concepts de la géométrie classique, à l'approche de la singularité classique, nous recevrions des rayons de courbure de plus en plus petits de l'espace-temps, et en conséquence, le rayon deviendrait encore plus petit que l'échelle de Planck de l'ordre de
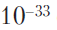voir (voir sections 1.1 et 1.5). La plupart des théoriciens, pensant à la gravité quantique, supposent qu'à de telles échelles, l'espace-temps serait déjà très différent de sa forme habituelle (variété lisse) (bien que dans la section 4.3, je présenterai des arguments complètement différents sur ce point). Que cela soit vrai ou non, il n'y a aucune raison de douter que les procédures de la relativité générale devront inévitablement être modifiées pour se combiner avec les méthodes de la mécanique quantique sur les approches d'une telle géométrie espace-temps radicalement courbée. Autrement dit, nous avons besoin d'une théorie de la gravité quantique adaptée à notre cas, qui nous permettrait de faire face à des situations dans lesquelles les procédures classiques d'Einstein conduisent à une singularité (mais à comparer avec la section 4.3).
Nous entendons souvent des déclarations selon lesquelles un tel précédent s'est déjà produit. Comme indiqué dans la section 2.1, au début du 20e siècle, un problème sérieux s'est posé avec les concepts classiques de l'atome, car, selon la théorie, les atomes auraient dû s'effondrer de manière catastrophique dans un état singulier, lorsque des électrons tomberaient en spirale sur le noyau (avec la génération d'une impulsion de rayonnement), et résoudre ce problème n'a été possible qu'avec l'avènement de la mécanique quantique. Ne faut-il pas s'attendre à ce que même en discutant d'un effondrement aussi catastrophique de l'Univers tout entier, la situation devienne plus claire au niveau de la mécanique quantique? Mais voici le hic: même maintenant, il n'y a pas d'hypothèse généralement acceptée de la gravité quantique. Plus grave encore est le fait que la plupart des hypothèses déjà avancées ne résolvent pas le problème de singularité - les singularités demeurent même dans une théorie quantifiée.Il y a quelques exceptions notables - l'hypothèse du rebond quantique non singulier [Bojowald, 2007; Ashtekar et al., 2006], mais je devrai revenir sur ce sujet dans les sections 3.9 et 3.11 (ainsi que dans la section 4.3), où je soutiens que de telles hypothèses ne donnent pas vraiment beaucoup d'espoir pour résoudre le problème de singularité dans notre Univers. ...
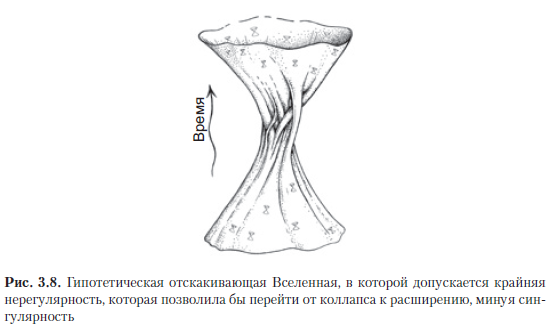
Une possibilité complètement différente d'éviter la singularité est associée à l'espoir que de petits écarts par rapport à la symétrie exacte présents au stade de l'effondrement de l'Univers pourraient augmenter radicalement à l'approche de la grande implosion, par conséquent, immédiatement avant l'effondrement complet, la structure de l'espace-temps ne correspondrait pas exactement au modèle FLRU. Par conséquent, on espère souvent que la singularité qui se manifeste dans les modèles FLRU peut être fausse et que dans une situation asymétrique plus générale, de telles singularités spatio-temporelles classiques ne se présenteront tout simplement pas; par conséquent, il y a lieu de s'attendre à ce que, dans le cas général, l'Univers qui s'effondre, en raison d'une géométrie spatio-temporelle intermédiaire complexe (figure 3.8), puisse se transformer en expansion irrégulière.Même Einstein lui-même a essayé d'avancer de tels arguments - que la singularité peut être évitée en rebondissant à partir d'un effondrement irrégulier [Einstein, 1931; Einstein et Rosen, 1935] ou parce que l'effondrement final et les singularités peuvent en quelque sorte empêcher les mouvements orbitaux des corps célestes [Einstein, 1939].
On peut soutenir qu'après un effondrement aussi presque singulier (mais pas strictement singulier), un état se produira, dont les perturbations se lisseront progressivement, et par conséquent ressemblera fortement au modèle FLRU en expansion (comme dans la figure 3.8). En 1963, ce problème a été analysé en détail par deux physiciens théoriciens soviétiques - Evgeny Mikhailovich Lifshits et Isaak Markovich Khalatnikov [Lifshits et Khalatnikov, 1963]. Leurs travaux montrent que, dans des conditions normales, de telles singularités n'apparaissent pas, ce qui conforte l'hypothèse de rebond non singulier décrite ci-dessus. En conséquence, il a été avancé qu'en relativité générale, les singularités spatio-temporelles qui surviennent lors de l'effondrement gravitationnel et apparaissent dans les solutions exactes connues de l'effondrement des modèles de Friedmann ou d'autres modèles FLRU sont générées uniquement parce queque les solutions connues ont des propriétés spécifiques irréalistes, par exemple une symétrie stricte. Par conséquent, de telles singularités ne se seraient pas développées dans les conditions de perturbations asymétriques typiques. Cependant, cette hypothèse n'a pas été confirmée, ce qui sera discuté dans la section suivante.
»Plus de détails sur le livre peuvent être trouvés sur le site de la maison d'édition
» Table des matières
» Extrait
Pour Habitants un rabais de 30% sur le coupon - Penrose
Lors du paiement de la version papier du livre, un e-book est envoyé à l'e-mail.