Théorie des quanta. Un univers d'ondes de probabilité

La théorie quantique est l'un des modèles les plus précis décrivant le monde qui nous entoure, et les solutions techniques développées grâce à l'utilisation de l'appareil de mécanique quantique sont fermement entrées dans la vie quotidienne de la société moderne. Et il est d'autant plus surprenant que la compréhension même des concepts de base de ce domaine de la connaissance entre en conflit sérieux avec l'intuition, non seulement des personnes éloignées de la science, mais aussi des chercheurs eux-mêmes, ce qui est confirmé par un grand nombre d' interprétations différentes . Dans cet article, je propose de considérer les concepts de base de la théorie quantique du point de vue le plus intuitif qui a semblé à l'auteur, une théorie quelque peu modifiée de la probabilité.



Que se passera-t-il si, par analogie avec l'expérience à deux fentes, tout l'espace sur le chemin de la particule vers l'écran est rempli de fentes?

« — , .»



« » —

C:

1. :
2. ,

:

Au début du XIXe siècle, le déterminisme dominait dans l'image scientifique du monde - la doctrine selon laquelle les paramètres initiaux d'un système déterminent complètement son développement ultérieur. La mécanique newtonienne a permis de prédire très précisément le comportement de corps pas trop grands se déplaçant à des vitesses bien inférieures à la vitesse de la lumière, et la théorie de la relativité spéciale et générale qui est apparue plus tard a rendu possible des calculs similaires pour des objets très massifs se déplaçant à des vitesses proches des vitesses de la lumière.



Et ce n'était qu'une question de temps que la création du démon de Laplace semblait être un dispositif informatique hypothétique qui serait capable de recevoir les paramètres initiaux de n'importe quel système en entrée et de calculer sa position à tout moment. Les scientifiques ont déjà commencé à anticiper une victoire presque complète sur l'incertitude et le triomphe de l'esprit humain, bien que les paradoxes associés à la possibilité même de l'existence du démon de Laplace fussent déjà mis en doute.







Mais à peu près au même moment, les tentatives des chercheurs pour pénétrer la structure de la nature à des échelles spatiales et temporelles extrêmement petites ont apporté de mauvaises nouvelles pour le déterminisme. Ainsi, l'un des principaux énoncés de la nouvelle théorie quantique, le principe d'incertitude, disait que si un système a des paramètres connectés (de navettage), plus nous mesurons l'un d'eux avec précision, moins nous pouvons déterminer l'autre avec certitude.



Sur la base de ces idées, aucun événement ne pouvait être prédit avec une précision absolue, car il y avait une certaine incertitude dans les mesures et ce fait n'était pas du goût de nombreux membres de la communauté scientifique de l'époque. Le camp des critiques était dirigé par Albert Einstein, qui avait déjà une autorité mondiale à l'époque, qui, par correspondance avec son adversaire et collègue Heisenberg - Max Born, a déclaré à propos de la possibilité du principe d'incertitude: "... En tout cas, je suis convaincu que [Dieu] ne joue pas aux dés."

Principe d'incertitude, tatouage et calligraphie

Le fonctionnement du principe d'incertitude est souvent attribué aux propriétés du processus de mesure lui-même, mais il existe des raisons plus fondamentales et le moyen le plus simple de les démontrer est par l'exemple de deux paramètres: l'impulsion et les coordonnées des particules. Tout comme un même dessin peut être réalisé de deux manières fondamentalement différentes: vecteur et raster, c'est-à-dire soit sous forme de lignes, comme, par exemple, en calligraphie, soit sous la forme d'un ensemble de points, comme dans le cas d'un tatouage. En outre, le mouvement d'une particule peut être décrit de deux manières alternatives: à l'aide de l'impulsion - le vecteur de la vitesse de masse$$$\vec p=m\vec v$ ou en utilisant un ensemble de coordonnées spatio-temporelles $$${(x_1,t_1);(x_2,t_2);...;(x_n,t_n)}$...

À gauche: Maître de la calligraphie dessine le symbole Enso (円 相,), source . À droite: Le processus de tatouage de la peau humaine, source .

Et selon le principe d'incertitude, plus nous fixerons avec précision la coordonnée d'un objet dans l'espace-temps $$$Δx$, moins nous pouvons obtenir d'informations sur son impulsion. Imaginez qu'une balle lancée soit photographiée par plusieurs photographes, chacun avec une vitesse d'obturation différente sur l'appareil photo. Si la vitesse d'obturation est longue, la position de la balle sur la photo se révélera floue, mais le vecteur de son mouvement sera clairement visible. Et plus la vitesse d'obturation est courte, plus la localisation du sujet sera claire et, à la limite, nous obtiendrons une boule claire suspendue dans les airs et nous ne pourrons pas du tout dire sur la trajectoire le long de laquelle il se déplaçait.

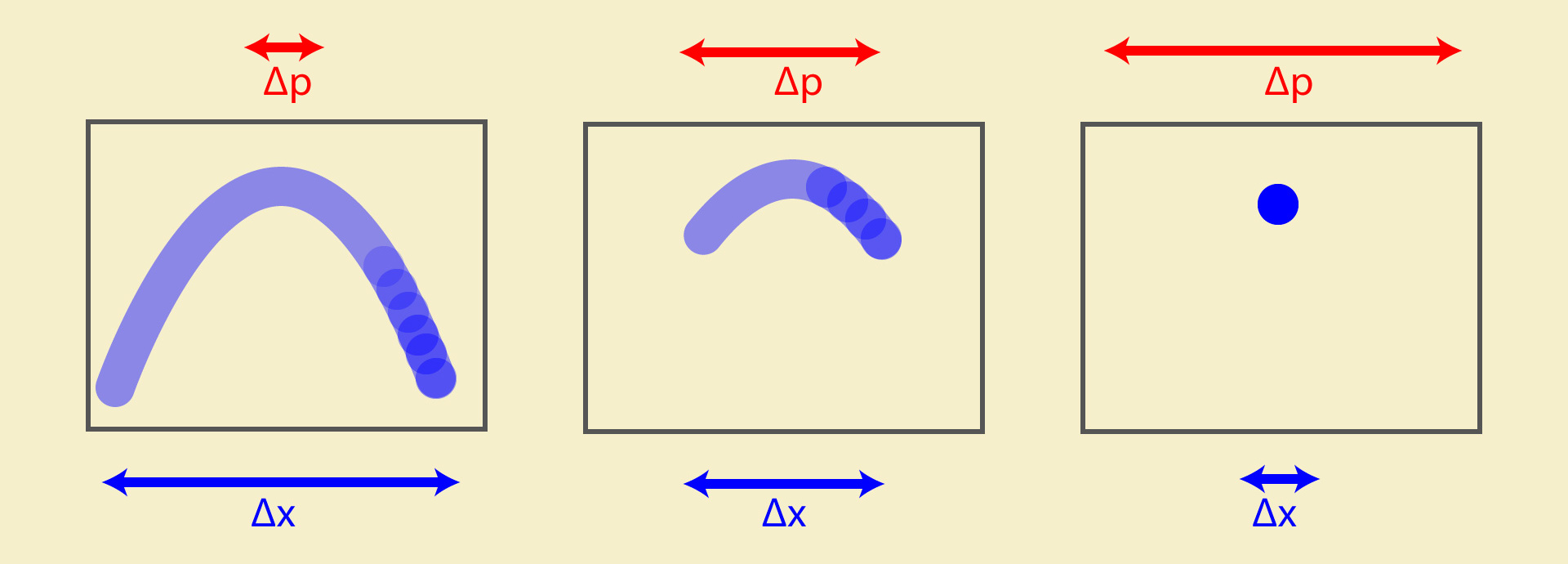
Trois plans alternatifs d'un objet en mouvement, de gauche à droite, montrent comment avec une augmentation de l'intervalle espace-temps (exposition de la caméra), la quantité d'informations sur l'impulsion (trajectoire des particules) diminue.

Dans le monde des objets macroscopiques, cet effet n'est pas un gros problème, et si nous voulons définir les coordonnées de la voiture avec une précision comparable à la taille de la voiture elle-même, alors il n'y aura pas de problème - la voiture peut entrer en toute sécurité dans le tunnel tout en conservant sa trajectoire prévisible. Mais si nous essayons de faire de même, par exemple, avec des photons et commençons à les transmettre à travers une fente décroissante, alors au début, la tache lumineuse deviendra, comme prévu, de plus en plus étroite, mais lorsque la taille de la fente deviendra comparable à la longueur d'onde des photons, alors les trajectoires des photons à la sortie de la fente deviendront de moins en moins prévisible et la tache lumineuse commencera à s'étendre en largeur. En d'autres termes, plus nous savons précisément où la particule a volé, moins nous saurons où elle se déplacera ensuite.

Ci-dessus, de gauche à droite: diagrammes d'interférence obtenus avec réduction de fente successive, source . Ci-dessous: schéma de principe du montage expérimental, source .

Les ondes de matière et leurs amplitudes

Mais il est difficile de surprendre quelqu'un avec l'interférence d'un rayon de lumière, car tout le monde sait déjà que la lumière est une onde, et chaque point du front d'onde sera également une source d'onde, et en réduisant l'écart, nous obtenons, selon le principe de Huygens-Fresnel , un front secondaire, qui avec la diminution la taille de la fente ressemblera de plus en plus à une onde provenant d'une source ponctuelle.

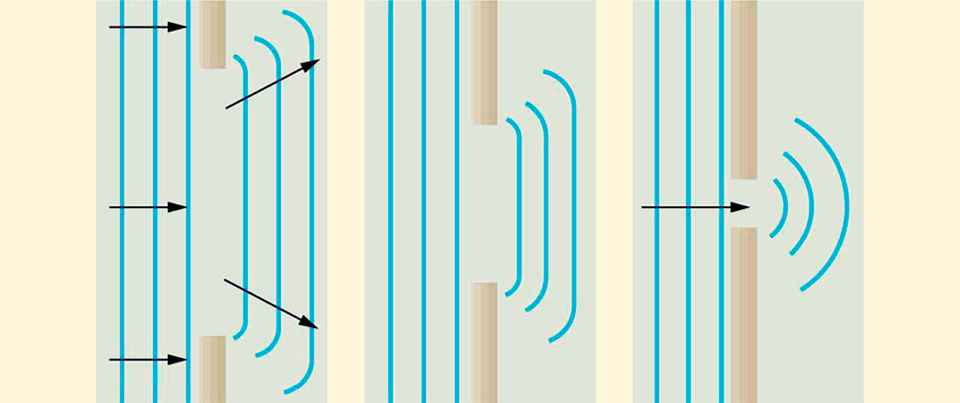
Diffraction du front d'onde avant passant par le trou, source .

En effet, toute vague de par sa nature géométrique n'est pas localisée en un point, car pour créer même la vague la plus simple, deux mesures sont nécessaires: l'amplitude de l'onde (hauteur) et la longueur d'onde (largeur). Et si nous commençons à compresser la vague en hauteur, elle s'étendra en longueur et vice versa. Mais plus intéressant encore, des expériences similaires ont été réalisées avec des particules de matière: des électrons, des atomes et même des molécules organiques, et elles ont toutes également démontré la diffraction des ondes.



Pour la première fois, l'idée que non seulement les photons, mais en général toute matière ont des propriétés d'onde, a été exprimée en 1923 par le physicien français Louis de Broglie dans son ouvrage " Waves and quantaCette hypothèse a été partiellement confirmée dès 1927, à la suite de l'expérience Davisson-Germer, qui a montré la diffraction des ondes d'électrons, qui a valu à Louis de Broglie un prix Nobel de physique bien mérité en 1929.



Plus tard, avec des électrons, l' expérience bien connue à deux fentes a été réalisée, qui a que les ondes de particules de matière peuvent non seulement subir une dispersion, formant des fronts d'ondes secondaires, mais ces ondes secondaires peuvent également s'amplifier, se rencontrer dans la même phase ou, au contraire, s'éteindre mutuellement, se rencontrer en antiphase, créant un motif d'interférence, similaire à la façon macroscopique vagues d'eau ou ondes sonores acoustiques.

: , . : , , .

Mais si les vagues dans l'eau - ce mouvement oscillatoire des particules d'eau haut et bas, les ondes sonores - est similaire au mouvement des molécules d'air, l'oscillation qui est une onde de matière, qui peut être un photon, un atome, molécule, humain? Formellement, les scientifiques ne sont jamais parvenus à un consensus sur ce score, néanmoins, ils ont appris à calculer la fonction qui décrit cette onde en fonction de la coordonnée ou de tout autre paramètre pouvant être mesuré et ont constaté que le carré du module de cette fonction est une estimation précise de la probabilité résultats de mesure. Par conséquent, de nombreux scientifiques, y compris le physicien exceptionnel Richard Feynman, l'ont appeléfonctions d'onde - avec amplitudes de probabilité. Et il peut sembler assez étrange que toute matière et rayonnement soient des ondes de certains concepts mathématiques abstraits, mais comme nous essaierons de le montrer plus loin, en acceptant cette affirmation, vous pouvez obtenir une explication assez claire de nombreux effets quantiques.

Nombres complexes et phase de probabilité

Des expériences avec une et deux fentes, nous savons déjà qu'à bien des égards les amplitudes de probabilité se comportent comme les ondes les plus ordinaires et peuvent même, en passant par une double fente, se chevaucher, augmentant ou vice versa diminuant la probabilité d'apparition d'une particule en un point, ce qui crée un motif d'interférence.

. : — . : . .

Et si nous définissons la probabilité d'un événement comme le rapport du nombre de résultats menant à un événement au nombre total de tous les résultats possibles, alors nous obtenons que la probabilité est un nombre positif, sur l'intervalle de zéro à un, mais ensuite, si nous prenons deux graphiques de densité quelconques la probabilité de trouver une particule en un point, nous verrons que l'addition des amplitudes de ces graphes sera toujours supérieure à chacun d'eux séparément et aucune interférence destructive ne sera obtenue.



Et si on ajoute une propriété aux ondes de probabilité qui les fait interférer? Imaginez une ligne droite et chaque point dessus correspondra à la coordonnée de la particule, puis à partir de chaque point nous reporterons perpendiculairement la probabilité correspondant à l'emplacement de la particule en ce point. Connecter le point$$$x$et la probabilité correspondante que nous obtenons un vecteur - plus la longueur du vecteur est grande, plus la probabilité de trouver une particule à ce point est grande, et pour que ces vecteurs puissent interagir, nous ajouterons également l'angle de rotation à la longueur et le prendrons en compte lors de l'ajout.



Vous avez probablement déjà deviné qu'une telle construction est très similaire aux nombres complexes, qui ont également un module - longueur et phase - un angle. Ensuite, chaque coordonnée correspondra à un plan complexe, dans lequel les vecteurs de probabilité tourneront comme les aiguilles d'une horloge, et s'ils regardent dans une direction, ils s'additionneront, et s'ils sont dans des directions opposées, ils seront soustraits. En reliant les extrémités de ces flèches, nous obtenons la forme de la fonction d'onde ou l' amplitude de la probabilité qu'une particule se déplace en ligne droite dans une dimension.

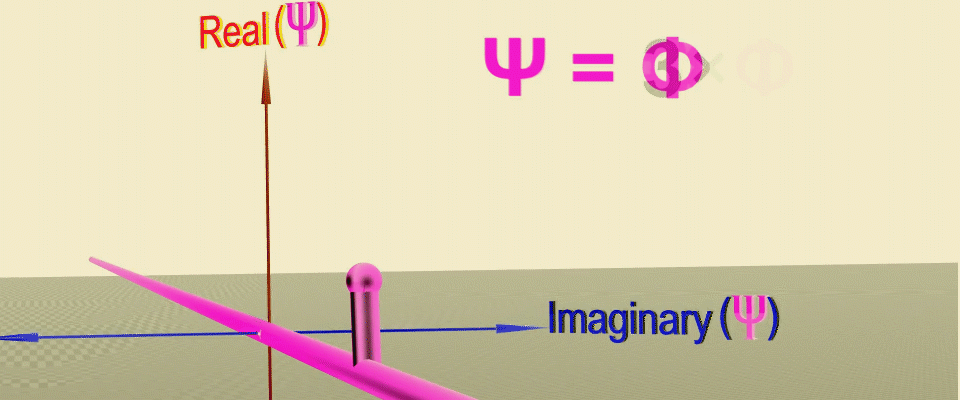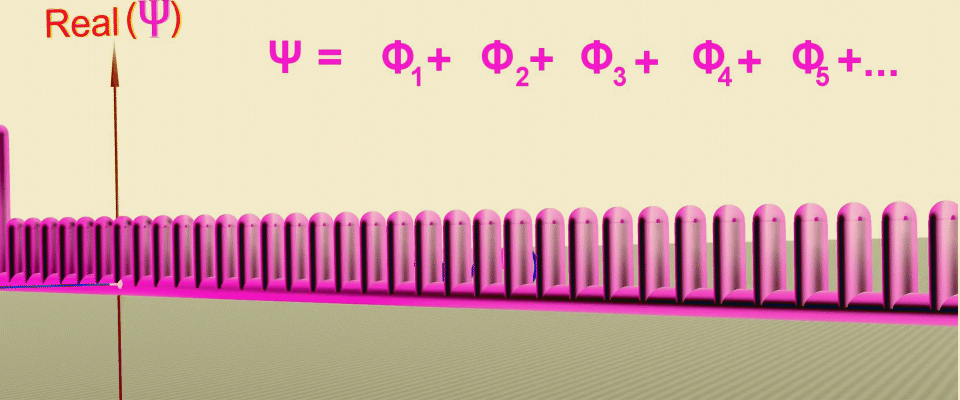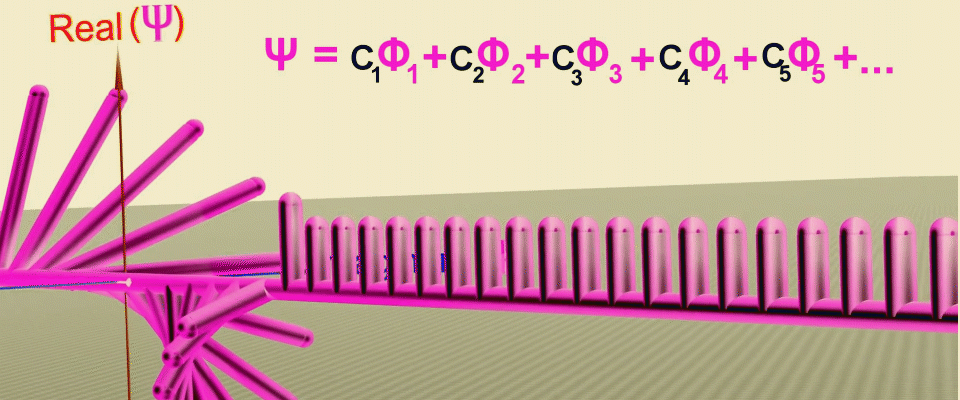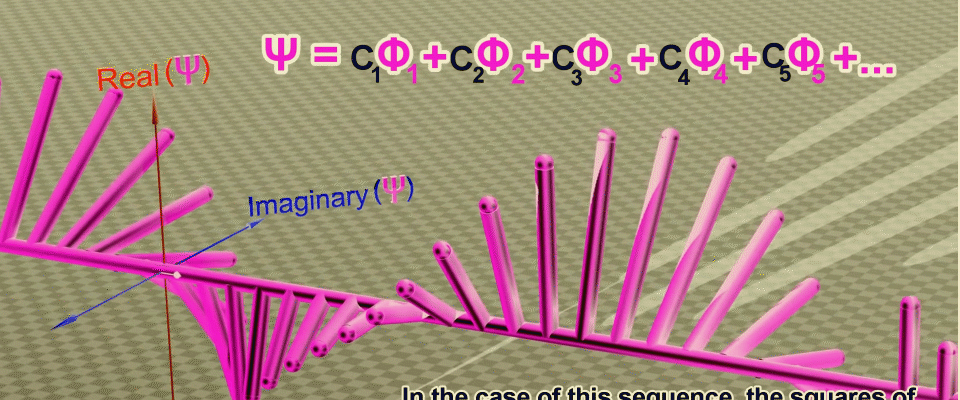
Animation de transformations successives qui vous permettent d'obtenir la fonction d'onde comme la somme des amplitudes de probabilité aux points le long du trajet des particules (ligne verte), d'abord la partie réelle de l'amplitude est définie, puis la phase (angle de rotation) dans le plan complexe. Source .

Les nombres complexes sont de la forme $$$z=x+y*i$où se trouve la première partie $$$x$ appelé réel, et le second - $$$y*i$- imaginaire. Ces deux composants ne se mélangent jamais, mais obéissent aux mêmes règles que les nombres réels ordinaires, en tenant compte du fait que$$$i$ Est une unité imaginaire et est égal à $$$\sqrt{-1}$...



L'un des axiomes de base de la théorie quantique, appelé la règle de Born , stipule que le carré du module de la fonction d'onde nous donne une fonction de densité de probabilité , c'est-à-dire, dans notre exemple, la distribution de probabilité de trouver une particule en fonction de la coordonnée.



Un rafraîchissement rapide en mémoire, le module d'un nombre complexe est la distance de l'origine -$$$(0, 0i)$ pointer avec des coordonnées $$$(x;yi)$, c'est à dire: $$$\sqrt{x^2+(y\sqrt{-1})^2}$, il est clair que $$$(\sqrt{-1})^2=-1$, mais nous n'effacerons pas l'unité imaginaire pour l'instant, mais trouverons le carré du module:

$$$\left(\sqrt{x^2+(y\sqrt{-1})^2}\right)^2=x^2+(y\sqrt{-1})^2=(x+y\sqrt{-1})(x-y\sqrt{-1})$

On obtient que le carré du module d'un nombre complexe est son produit par le même nombre complexe, qui ne diffère que par le signe avant le coefficient de la partie imaginaire $$$z=x-y*i$... Ces paires de nombres sont appelées conjuguées complexes et sont des réflexions en miroir l'une de l'autre, correspondant à la rotation de vecteurs dans le plan complexe par des angles égaux, mais dans des directions opposées.

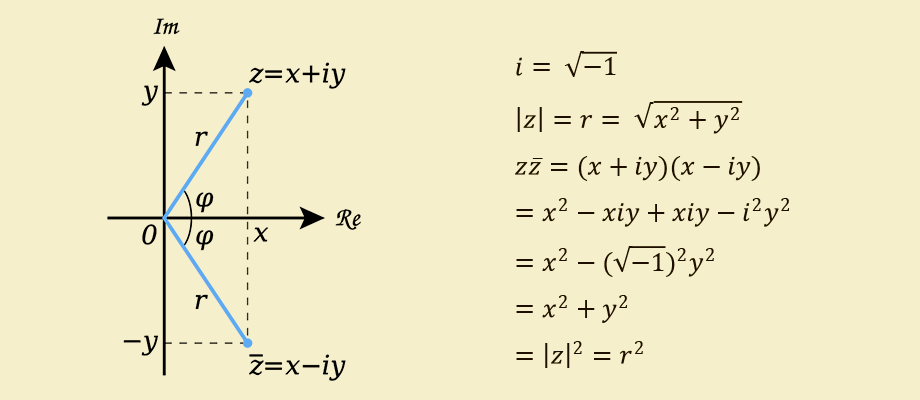
Où: $$$\overline z$ - nombre conjugué complexe

Le monde réel des unités imaginaires

Voici ce que nous avons déjà compris: la fonction d'onde attribue un certain nombre complexe à chaque coordonnée. En fait, c'est ce que font les fonctions d'onde - elles mettent en correspondance avec un paramètre mesurable un nombre complexe, dont l'angle de rotation est appelé la phase. Les phases de nombres complexes sont responsables des effets d'interférence de l'amplification et de l'atténuation des probabilités, qui sont obtenus en multipliant la fonction d'onde par sa propre réflexion miroir - conjugaison complexe.



Lorsqu'on lui a demandé pourquoi le carré du module de la fonction d'onde donne la densité de probabilité, la théorie quantique répond généralement - tais-toi et comptecar le carré du module fait un réel à partir d'un nombre complexe. Bien sûr, cette réponse ne nous convient pas du tout, car à partir d'un nombre complexe, vous pouvez en obtenir un réel en prenant simplement son module, alors j'aimerais comprendre la signification de la quadrature du module.



Imaginons que nous ne sachions rien sur la fonction d'onde ou la fonction de densité de probabilité, mais que nous ayons simplement fait de nombreuses observations et marqué par des points où et à quelle fréquence la particule apparaît. En même temps, nous comprenons que la distribution résultante doit être décrite par une sorte de graphique de la fonction de densité de probabilité et il serait extrêmement utile de connaître cette fonction elle-même.



Pour savoir quelle fonction correspond à nos points, allons de la manière la plus simple et commençons à adapter la réponse aux données, c'est-à-dire à sélectionner des polynômes qui passeront par le nombre maximum de points disponibles. Commençons par deux points et sélectionnons pour eux les coefficients du polynôme du premier degré, c'est-à-dire la fonction linéaire$$$y = ax + b$car la ligne passera exactement par nos deux points. S'il y a des points qui ne se trouvent pas sur cette ligne, alors nous prenons un polynôme du second ordre$$$y = ax^2 + bx + c$dont le graphique est constitué de diverses paraboles, en choisissant les coefficients, nous sommes assurés d'obtenir au moins trois points, dont l'un sera un sommet et les deux autres se trouveront sur les côtés. Ensuite, nous vérifions à nouveau s'il y a encore des points situés en dehors du graphe, si c'est le cas, nous répétons en augmentant le degré du polynôme d'un de plus et ainsi de suite, la logique est claire, le polynôme de degré$$$n$ garanti de passer $$$n+1$points et en conséquence nous pouvons choisir un polynôme qui couvrira tous nos points. Il existe même un théorème spécial - le théorème d' approximation de Weierstrass , qui confirme que c'est possible.

Un exemple de points d'ajustement tirés de la fonction de densité de probabilité d'une distribution normale avec des polynômes de divers degrés, de linéaire au 18e degré, en utilisant la fonction numpy.polyfit . Vous pouvez vous assurer que le degré du polynôme correspond au nombre de points par lesquels passe son graphe.

Code Python:

from numpy import *
from matplotlib.pyplot import *
from mpl_toolkits.axes_grid.axislines import SubplotZero


mu, sigma = 0, 0.1
x = np.arange(-1,1,0.02)
y = 1/(sigma * np.sqrt(2 * np.pi))*np.exp( - (x - mu)**2 / (2 * sigma**2) )

y1 = poly1d(polyfit(x,y,1))	# linear
y2 = poly1d(polyfit(x,y,2))	# quadratic
y3 = poly1d(polyfit(x,y,3))	# cubic
y4 = poly1d(polyfit(x,y,4))	# 4th degree
y5 = poly1d(polyfit(x,y,10))	# 10th degree
y6 = poly1d(polyfit(x,y,18))	# 18th degree

fig = figure(figsize=(20,8), facecolor='#f4efcb', edgecolor='#f4efcb')
ax = SubplotZero(fig,111)
fig.add_subplot(ax)

ax.plot(x,y1(x),'r',label=u'')
ax.plot(x,y2(x),'g',label=u'')
ax.plot(x,y3(x),'orange',label=u'')
ax.plot(x,y4(x),'b',label=u'$4$ ')
ax.plot(x,y5(x),'c',label=u'$10$ ')
ax.plot(x,y6(x),'m',label=u'$18$ ')
ax.plot(x,y,'k.',label=u'')

ax.set_xlabel(u'x')
ax.set_ylabel(u'y')
ax.set_facecolor('#f4efcb')
ax.minorticks_on()
ax.legend(frameon=False,loc=8,labelspacing=.2)
ax.annotate('  18 :'+'\n'+str(y6.coeffs), xy = (-1,1.2))

setp(ax.get_legend().get_texts(), fontsize='large')

fig.savefig("Curve fitting.svg",bbox_inches="tight",pad_inches=.15)

Et comme la densité de probabilité peut être approximée par un polynôme, alors ce polynôme a sûrement des racines et un autre théorème merveilleux, le théorème principal de l'algèbre dit que oui, tout polynôme doit avoir des solutions en nombres complexes, et si les racines sont réelles, cela signifie simplement que la partie imaginaire est égale à zéro (les vecteurs auront un angle de rotation nul), puisque l'ensemble des nombres réels est complètement contenu dans l'ensemble des complexes$$$\mathbb{R} \subset \mathbb{C}$...



Et si un nombre complexe$$$z=x+y*i$ est la racine d'un polynôme, alors automatiquement la racine de la même équation est le nombre qui lui est conjugué $$$\overline z=x-y*i$, un autre théorème nous en dit long - le théorème sur les racines conjuguées complexes .



Par exemple, imaginons que la densité de probabilité soit décrite par un polynôme du deuxième degré$$$x^2+5*x+6,5$et trouve ses racines. Par la formule des racines d'une équation quadratique$$$x_{1,2} = \frac{-b \pm \sqrt{b^2-4ac}}{2a}$en substituant les coefficients $$$a=1, b=5, c=6,5$ et on obtient sous forme de solution deux nombres complexes conjugués $$$x_1=-5/2 + i/2$, $$$x_2=-5/2 - i/2$, comme l'affirme le théorème des racines conjuguées.



Par contre, connaissant les racines et utilisant les formules de Vieta, nous pouvons décomposer le même trinôme carré comme suit:$$$x^2+bx+c=(x-x_1)(x-x_2)$il est facile de vérifier que c'est vrai, en substituant les valeurs obtenues et en ouvrant les crochets, on obtient le polynôme d'origine. Mais en même temps, sur le côté droit de la formule Vieta, nous avons obtenu le produit de deux nombres complexes conjugués, qui est le carré du module. En principe, la même logique peut être étendue à d'autres degrés de polynômes, l'essentiel est que les racines iront toujours par paires, et leur multiplication sera utilisée pour obtenir le polynôme d'origine.



Bien sûr, il s'agit d'un raisonnement très vague, conçu pour comprendre en quelque sorte ce qui se passe et, à l'aide d'un exemple simple, montrer que les nombres complexes sont pleinement justifiés et que leurs produits conjugués peuvent donner quelque chose de similaire à une densité de probabilité.

Une bande dessinée avec une blague sur le thème des nombres réels et la multiplication d'une fonction d'onde par sa propre conjugaison complexe. Une source

D'accord, supposons que nous ayons une idée du fonctionnement des amplitudes de probabilité, de leur complexité et de la manière dont les probabilités ordinaires en découlent. Et nous pouvons passer à la question de savoir ce que ces probabilités prédisent pour nous, c'est-à-dire des résultats des mesures .

Fonction d'onde et densité de probabilité

En obtenant la densité de probabilité de trouver une particule dans une certaine coordonnée, nous prédisons la fréquence avec laquelle nous observerons la particule à différents points. Par exemple, si la densité de probabilité est décrite par une courbe gaussienne, comme sur le côté gauche de la figure ci-dessous, alors dans$$$68\%$ cas nous verrons que la particule apparaît sur l'intervalle de $$$-1\sigma$ avant $$$+1\sigma$et en $$$95\%$ cas sur le segment de $$$-2\sigma$ avant $$$+2\sigma$etc. Ce qui, dans le cas d'une distribution symétrique bidimensionnelle, illustrée à droite, donnera une densité de détection plus élevée d'une particule dans une zone circulaire au centre et une faible densité lorsqu'elle s'éloigne du centre:







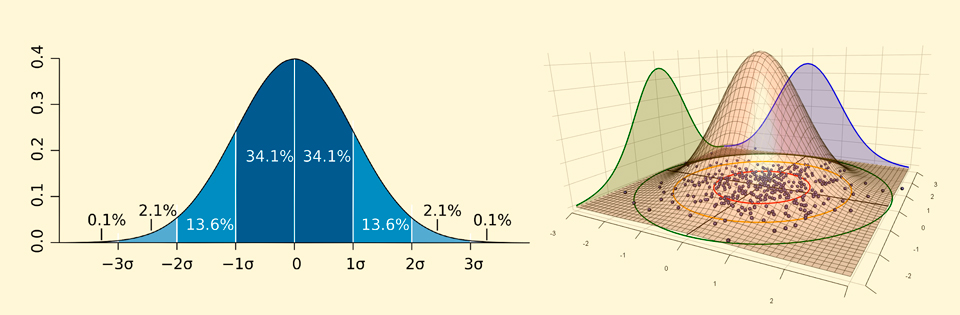
Un schéma assez simple: la fonction d'onde de la coordonnée définit la forme de la distribution, qui nous indique alors les probabilités de mesurer une particule en un point de l'espace. Néanmoins, une telle interprétation peut conduire à d'étranges contradictions et il est parfois plus naturel de penser les particules comme des ondes d'amplitudes de probabilité. Par exemple, l'image ci-dessous, à gauche, montre à quoi ressemble la densité de probabilité d'un électron interagissant avec un noyau d'hydrogène. Conformément à ce graphique, vous pouvez obtenir la forme des orbitales dites électroniques - régions autour du noyau d'un atome dans lesquelles l'interaction avec un électron est le plus probable, illustrée à droite:





Gauche: courbes de densité de probabilité de trouver un électron autour d'un seul proton, pour trois niveaux d'énergie$$$1s, 2s, 3s$... À droite: montre un exemple de ce à quoi ressembleraient les distributions des points lors de la mesure des coordonnées d'un électron. Source .



Dans la figure ci-dessus, vous pouvez voir comment les formes des orbitales changent en fonction du niveau d'énergie de l'électron - plus l'énergie de l'électron est élevée, plus le rayon de la coquille est grand, ce qui est tout à fait compréhensible, car plus il y a d'énergie, plus l'électron peut résister à l'attraction du noyau et plus du noyau, il peut interagir, mais en même temps, à chaque nouveau niveau d'énergie, une section avec une probabilité nulle est ajoutée, appelée un nœud, ainsi, par exemple, l'orbitale électronique au 3ème niveau d'énergie a la forme d'une sphère en couches contenant deux zones à l'intérieur, la probabilité détection d'un électron dans lequel est zéro.





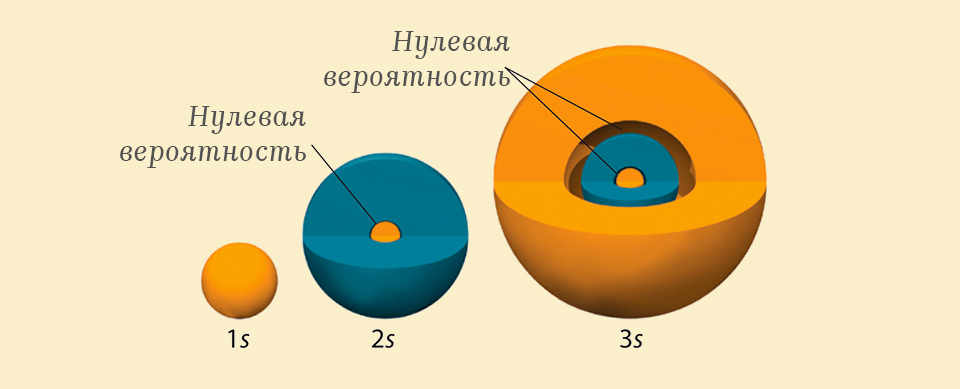
Le contour de la probabilité de trouver un électron au voisinage du noyau d'un atome d'hydrogène pour trois niveaux d'énergie de gauche à droite: 1s, 2, s 3s. Source .



Une telle distribution de probabilité semble très étrange, car il est impossible d'aller d'une sphère à une autre sans croiser celle imbriquée entre elles.



Mais si vous pensez à un électron comme une amplitude de probabilité, alors tout est expliqué assez naturellement, dans l'image ci-dessous se trouve la fonction d'onde du rayon d'un électron autour du noyau d'hydrogène, calculée en une dimension, pour trois niveaux d'énergie.







En regardant les graphiques de la fonction d'onde, il est plus facile de comprendre qu'un électron détenu par le noyau d'un atome est une onde stationnaire et, comme toute onde stationnaire, il aura des soi-disant nœuds (nœud ) - zones où l'amplitude sera nulle en raison d'une interférence avec l'onde réfléchie.



Un exemple de la formation de nœuds d'interférence (points rouges) dans une onde stationnaire unidimensionnelle, source .



Et si une onde unidimensionnelle, comme dans l'animation ci-dessus, ne ressemble toujours pas à la forme d'une couche d'électrons tridimensionnelle en couches d'un atome d'hydrogène, alors je propose d'imaginer une onde sur un plan bidimensionnel se propageant à partir d'une source ponctuelle. Donc, pour voir la forme complète d'une telle onde bidimensionnelle , vous devez la regarder en troisdes mesures. Et pour un habitant d'un monde à deux dimensions, une telle onde ne sera qu'un ensemble de cercles divergeant du centre. De même, avec des ondes tridimensionnelles - elles vivent en quatre dimensions, mais pour nous, elles ressembleront à des sphères tridimensionnelles divergentes.





Droite: Animation d'une onde se propageant sur une surface 2D. Gauche: Un exemple de ce à quoi ressemblerait la projection de cette onde sur un plan.

Barrière de décohérence quantique

Abraham Pais est un éminent physicien et historien des sciences qui a collaboré avec une galaxie de légendes scientifiques du XXe siècle, notamment: John von Neumann, Albert Einstein, Niels Bohr, Max Born, Paul Dirac, Wolfgang Pauli et bien d'autres. décrivant l'un des dialogues concernant le problème de l'observateur en physique quantique, il cite une question que lui pose Einstein:

"Pensez-vous vraiment que la lune n'existe que lorsque vous la regardez?" (Rev. Mod. Phys. 51, 863-914 (1979), p. 907).

Et en effet, l'ancien dilemme philosophique sur l'existence de la réalité objective, avec la découverte des propriétés quantiques de notre monde, est devenu encore plus pertinent. La fonction d'onde permet de prédire le résultat de la mesure avec la précision requise, mais existe-t-elle indépendamment du contexte de la mesure et de l'observateur, et comment le vérifier?



Tout d'abord, il est nécessaire de définir ce que sont l'observation et la mesure . Pour mesurer la taille d'un objet, nous lui appliquons une règle, pour mesurer la température - nous appliquons un thermomètre pour mesurer la vitesse - nous envoyons une onde électromagnétique vers lui.



Dans tous ces cas, nous avons besoin de l'interaction de l'objet mesuré avec un autre objet, dont nous pouvons préparer l'état au préalable, un tel objet sera appelé un système de mesure. Ils ont secoué le thermomètre - préparé le système de mesure, mis l'aisselle - fait une interaction, puis évalué à quel point l'état du système de contrôle avait changé. C'est un principe général, toute mesure est l' interaction du système mesuré avec celui de contrôle.



Toute observation est aussi une mesure, en observant quelque chose, nous obtenons des informations sur un objet à l'aide de systèmes de mesure intégrés à notre corps, qui interagissent également avec l'objet. Si nous regardons un objet, nous interagissons avec les photons émis par cet objet, qui, tombant sur la rétine de l'œil, conduisent à une cascade complexe d'interactions et au lancement d'un signal nerveux qui pénètre dans le cerveau.

« ? … . , , , . , … : “ , , ”».



«. » —

Le principe de superposition des ondes nous dit que lorsque deux ou plusieurs ondes se rencontrent en un point de l'espace, le résultat de l'interaction sera une nouvelle onde, qui est la somme de leurs amplitudes. Ensuite, le résultat de la mesure sera toujours une superposition des fonctions d'onde du système mesuré et du système de mesure .



Maintenant, une question raisonnable se pose: si nous acceptons l'affirmation que tout est constitué d'ondes d'amplitudes de probabilité, alors pourquoi vivons- nous si ennuyeusement sans observer les propriétés des ondes telles que la superposition et l'interférence dans les objets macroscopiques qui nous entourent?



Pour répondre à cette question, revenons à l'expérience de la double fente: les électrons volent à travers la double fente un par un et frappent l'écran, sont marqués dessus avec un point; lorsque ce processus est répété plusieurs fois, les points forment un motif d'interférence qui correspond au passage d'une onde à travers deux fentes.

A gauche: animation du motif d'interférence à partir du passage d'une onde à travers une double fente, source . Droite: Résultats d'une expérience sur l'enregistrement d'électrons simples après avoir traversé une double fente. Source: New Journal of Physics, volume 15, mars 2013 .

Mais si nous voulons savoir par quelle fente l'électron passe et placer un appareil de mesure devant l'une d'entre elles, alors le motif d'interférence sur l'écran disparaîtra et nous ne verrons que deux pics à l'écran. Tout cela est déroutant, et on pourrait avoir l'impression qu'il existe une règle spéciale qui dit à l'électron que si personne ne regarde, alors il se propage sous la forme d'une onde, et quand ils essaient de la mesurer, il se transforme en une particule localisée. Cela semble très étrange, car garder autant de règles complexes pour un seul électron n'est pas du tout dans l'esprit de la nature.

Un dessin animé qui se moque de la séparation des phénomènes en quantique et classique. Source (http://www.bourbaphy.fr/zurek.pdf)

Et si nous n'appliquons que le principe de superposition, pouvons-nous obtenir les mêmes effets observés? Donc si d'abord nous avons une fonction d'onde qui décrit la coordonnée de l'interaction d'un seul électron avec l'écran$$$|\psi \rangle$, puis après avoir traversé la double fente, ce sera la somme de deux fonctions d'onde - passées à travers la fente $$$1$ et à travers l'écart $$$2$, alors l'état général peut s'écrire comme une superposition de ces deux états$$$\psi =\psi_1 +\psi_2$...



Dans le cas d'une fonction d'onde, afin de trouver la probabilité de l'interaction des particules en un point, nous multiplions la valeur de la fonction d'onde en ce point par sa propre conjugaison complexe, les unités imaginaires s'annulent, et nous obtenons la probabilité classique:

$$$p(x_j)=|\psi(x_j)|^2= z _j^* z_j= |z_j|^2$

Dans le cas d'une superposition de deux routes possibles, on multiplie la somme des fonctions d'onde:

$$$p(x_j)=|\psi_1(x_j)+\psi_2(x_j)|^2=$

$$$= (z1 _j^*+ z2 _j^*)(z1 _j+ z2 _j)=$

$$$= |z1 _j|^2+z1 _j^*z2 _j+z2 _j^*z1 _j+|z2 _j|^2$

Dans l'expression ci-dessus, en plus des modules de nombres complexes, nous avons également reçu des termes de la forme: $$$z1 _j^*z2 _j$ et $$$z2 _j^*z1 _j$ produits de différents nombres complexes, dont le résultat dépendra de l'angle de phase $$$φ$ ces nombres complexes:

$$$z1z2=|z1|⋅|z2|[cos(φ1+φ2)+isin(φ1+φ2)]$

Pour comprendre comment les phases des deux itinéraires alternatifs vont interagir, imaginez la phase comme une flèche qui tourne à une vitesse donnée, à mesure que l'onde se propage, un tour complet de la flèche correspond à la longueur d'onde, et la vitesse de rotation correspond à la fréquence.

La flèche noire montre une comparaison de la "vitesse de rotation" des phases de deux paquets d'ondes avec des fréquences de source différentes .

Puisque deux fonctions d'onde alternatives sont obtenues en divisant un original, il est raisonnable de supposer que leur fréquence et leur longueur d'onde seront les mêmes et les flèches des ondes résultantes tourneront à la même vitesse. Sur cette base, la différence de phase, lors de la rencontre en un point de l'écran, ne dépendra que de la différence de distance parcourue par l'onde jusqu'à ce point.



Cela signifie qu'en un point situé à égale distance de chacun des trous, les ondes se rencontreront avec la même position des flèches, c'est-à-dire en une phase et à cet endroit, nous verrons un pic dans le motif d'interférence, et au point où la différence des distances parcourues sera la moitié de la longueur vagues - les flèches des vagues se rencontreront dans des positions opposées et des interférences destructrices se produiront, ce qui donnera une tache sombre. Si vous vous déplacez un peu plus jusqu'à un point où la différence est une longueur d'onde entière, les flèches coïncideront à nouveau, et ainsi de suite.

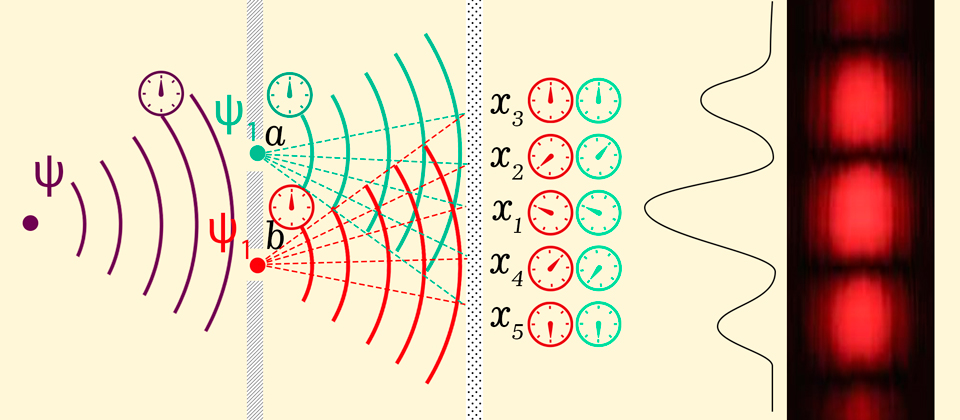
L'apparition de deux possibilités alternatives de frapper l'écran conduit à la division de la fonction d'onde d'origine en deux avec les mêmes phases, représentée sous la forme d'un cadran avec une flèche. La même phase implique la même vitesse de rotation de la flèche. En frappant un point sur l'écran au moment de la même position des flèches, les ondes interfèrent de manière constructive, si les flèches sont dirigées dans des directions opposées, une interférence destructive se produit.

Où les interférences disparaissent-elles lorsque nous mesurons, par quelle fente l'électron passe-t-il? Après avoir traversé le détecteur, non pas deux, mais bien d'autres variantes différentes de la fonction d'onde apparaissent, car même si le détecteur est microscopique, il sera toujours constitué d'un grand nombre d'atomes, par exemple, même un centième de gramme de fer contient environ$$$10^{20}$atomes, mais le nombre spécifique n'est pas important pour nous maintenant, l'essentiel est qu'une grande variété d'options d'interaction différentes apparaissent, qui dépendent de l'état spécifique des particules du détecteur, et chaque état alternatif donnera sa propre version alternative de la fonction d'onde.



Prenez aussi$$$p(x_j)=|\psi(x_j)|^2$ Est la probabilité qu'un électron atteigne la coordonnée $$$x_j$ sur l'écran, après avoir traversé le détecteur et à nouveau écrire cette probabilité en superposant toutes les trajectoires alternatives possibles:



$$$\psi(x) = \psi_1(x)+\psi_2(x)+...+\psi_n(x)$où $$$n$ - un très grand nombre d'options différentes pour l'état du détecteur.

$$$p(x_j)=|\psi_1(x_j)+\psi_2(x_j)+...+\psi_n(x_j)|^2=$

$$$= (z1 _j^*+ z2 _j^*+...zn _j^*)(z1 _j+ z2 _j+...+zn _j)=$

$$$= (\sum_{j=1}^n z_j^*)(\sum_{j=1}^n z_j)$

Pour plus de clarté, nous écrivons le résultat de la multiplication de ces sommes sous la forme d'une matrice de $$$n^2$ éléments:

$$$\begin{bmatrix} (z1^*)(z1) & (z1^*)(z2) & \cdots & (z1^*)(zn) \\ z2^*)(z1) & (z2^*)(z2) & \cdots & (z2^*)(zn) \\ \vdots & \vdots & \ddots & \vdots \\ (zn^*)(z1) & (zn^*)(z2) & \cdots & (zn^*)(zn) \end{bmatrix}$

Total nous avons $$$n$ - probabilités classiques le long de la diagonale et $$$(n^2-n)$et les termes d'interférence, et tout cela dans la somme donne la probabilité qu'un électron frappe pour un point. Mais dans ce cas, les termes d'interférence n'auront plus la même phase, comme dans le cas précédent, lorsque l'onde soit passée à travers la fente sans interaction, soit était complètement réfléchie. Maintenant, en passant par un détecteur composé de diverses particules non synchronisées entre elles, les fonctions d'onde résultantes auront également des phases aléatoires - incohérentes.



Ces états désynchronisés sont appelés états mixtes.). Et bien que les fonctions d'onde des états mixtes interfèrent également, le résultat de l'interférence ne dépendra plus de la distance parcourue par l'onde, et à chaque point de l'écran, on peut s'attendre au même et très grand nombre de termes interférents constructivement et destructivement, qui en moyenne donneront leur contribution nulle. ... Tout comme les impacts des molécules de gaz ne déplacent pas l'objet de sa place, puisque à chaque instant l'objet reçoit à peu près le même nombre d'impacts de toutes les directions.

Perte de cohérence de la fonction d'onde $$$1$ après avoir passé le détecteur $$$d$ conduit à une remise à zéro de la contribution des termes d'interférence en des points de l'écran et à l'apparition d'un motif correspondant à la superposition de deux pics gaussiens.

Dans le cas général, toute interaction d'un système quantique avec l'environnement extérieur conduit inévitablement et très rapidement à un mélange d'états, et, par conséquent, à une désynchronisation de phase et à un moyennage d'états alternatifs - la décohérence.



Par conséquent, notre version de la réponse à la question: pourquoi n'observons-nous pas d'effets quantiques dans des objets macroscopiques dans des conditions normales? différents domaines, ce qui est très difficile à mettre en œuvre dans la pratique. En d'autres termes, le chat de Schrödinger serait mort même dans la préparation des conditions nécessaires pour créer sa superposition, bien avant que la particule radioactive qui brise l'ampoule avec du poison ne se désintègre.

Un peu de cryptographie quantique

Le fait que votre smartphone ne dispose toujours pas de processeur quantique, vous devez également blâmer la décohérence. Après tout, même les implémentations les plus modernes d'ordinateurs quantiques occupent une pièce entière, et l'essentiel de leurs conceptions sont des systèmes de refroidissement et de blindage cryogéniques.

Schéma de construction de l'ordinateur quantique D-Wave 2000Q, source .

Mais si la décohérence est un gros problème dans la création d'ordinateurs quantiques, alors en cryptographie, le changement inévitable de la fonction d'onde pendant la mesure s'est avéré utile. Par exemple, si nous prenons un photon comme un bit quantique, alors, en fonction de son angle de polarisation, nous pouvons choisir deux options de codage différentes pour zéro et un:

• $$$0$ - polarisation verticale, $$$1$ - horizontal;
• $$$0$ - polarisation diagonale, $$$1$ - antidiagonal.

Désignons ces deux méthodes de codage comme deux bases: $$$VH$ et $$$DA$, respectivement. Alors si l'expéditeur - Alice encode un peu dans la base$$$VH$, c'est-à-dire qu'il envoie un photon polarisé horizontalement ou verticalement, le récepteur Bob devra alors faire passer le photon reçu à travers un filtre polarisant linéaire, qui bloque complètement la polarisation verticale.



Ensuite, si un photon vole à travers le polariseur et frappe le détecteur, nous savons avec certitude qu'il était polarisé horizontalement$$$0$, et s'il ne vole pas - verticalement - $$$1$... De même, si vous tournez le filtre polarisant en position verticale, il bloquera$$$100\%$ photons polarisés horizontalement.

Gauche: un photon orienté verticalement est bloqué par un filtre polarisant linéaire. Droite: lorsque vous tournez le filtre polarisant sur$$$90°$un photon polarisé verticalement passe librement. Source .

Jusqu'à présent, tout est parfaitement compatible avec le système de codage d'image classique. Mais en raison du principe de superposition, nous pouvons représenter un photon diagonal comme une composition de polarisation horizontale et verticale, et si nous le passons ensuite à travers un polariseur orienté vers le filtrage des photons verticaux, alors la sortie n'aura qu'une composante horizontale avec une amplitude$$$1/2$ de l'original, qui dans le cas d'un photon unique correspondra à $$$50\%$ la probabilité de traverser le filtre.

A gauche: un photon diagonal (flèche rouge) présenté comme une composition des composantes horizontale et verticale (flèches roses et violettes) du champ électromagnétique. Côté droit: un filtre polarisant linéaire bloque la composante verticale d'un photon diagonal et produit un photon polarisé horizontalement. Une source

Cela signifie que si nous encodons chaque bit suivant sur une base choisie au hasard, le destinataire devra également modifier la rotation du filtre polarisant, car s'il mesure un photon encodé sur une base horizontalement-verticale $$$VH$ avec le filtre tourné sous $$$45°$alors il recevra $$$0$ et $$$1$ aléatoirement avec probabilité $$$50\%$, ce qui équivaut à une perte complète d’informations.

En passant par un polariseur linéaire vertical, les photons diagonaux et antidiagonaux perdent la composante horizontale et la sortie est un photon horizontal d'amplitude $$$1/2$de l'original. Source .

Le premier protocole de cryptographie quantique est basé sur ce principe - $$$BB84$qui vous permet de transférer la clé de cryptage sur un canal ouvert. Donc, si Alice a besoin d'envoyer à Bob un message composé de n caractères, le moyen le plus fiable serait de traduire chacun des caractères en un code binaire, puis de prendre une séquence de zéros aléatoires et de uns de la même longueur et d'effectuer l'opération d'addition au niveau du bit XOR, c'est-à-dire si les caractères avec les mêmes indices coïncident alors en conséquence nous obtenons 0, et s'ils diffèrent alors$$$1$...



Ainsi, Alice reçoit un message chiffré et une clé, si le destinataire Bob a également une clé, alors il peut refaire l'opération XOR et récupérer le message d'origine. La physique de la cryptographie quantique vous permet simplement d'échanger une clé, donc dans l'algorithme$$$BB84$non pas une mais deux séquences de bits aléatoires sont générées à la fois avec une certaine marge concernant le message. La première séquence indique sur quelle base le photon, qui est le bit quantique de la clé envoyée par Alice-Bob, sera codé . Puis Bob , recevant des photons, également en utilisant une séquence aléatoire, choisit sur quelle base mesurer chaque photon, alors qu'il recevra un résultat incorrect avec la probabilité$$$25\%$...



Après avoir terminé le transfert de la clé quantique, il est nécessaire de se débarrasser des erreurs, pour cela, la procédure dite de tamisage de clé est appliquée , quand Alice envoie à Bob une séquence de bases dans laquelle la clé a été encodée simplement via le canal classique, après quoi Bob vérifie cette séquence avec celle dans laquelle il a mesuré les photons à la réception de la clé et renvoie à Alice les positions qui se sont avérées erronées. Alice biffe les positions erronées et la clé obtenue est ensuite utilisée pour le cryptage.



L'astuce quantique est que si un espion est connecté au canal, disons - Eve, qui va intercepter un photon, le mesurer et le diriger plus loin vers Bob , puis mesurer les photons interceptés avec une base mal choisie, cela détruira également inévitablement la superposition. Ainsi, même après le tamisage, il y aura toujours des erreurs dans la clé de Bob qui peuvent être détectées pendant le processus de vérification, quand Alice envoie un fragment de sa clé à Bob via le canal classique, si aucune erreur n'est trouvée à la suite de la vérification, alors vous pouvez utiliser la clé en toute confiance pour la messagerie.

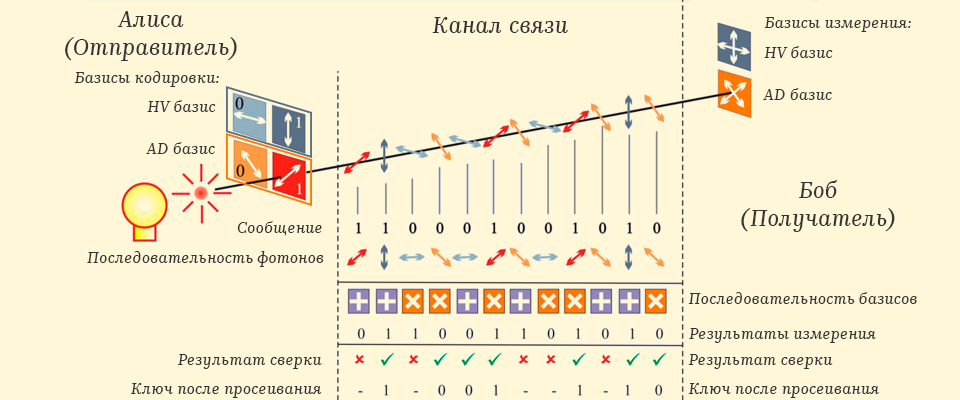
Diagramme logique de l'algorithme de chiffrement $$$BB84$... Source .

Conclusion

J'espère qu'à partir de cet article, vous avez pu glaner des informations et avoir une impression générale de la façon dont la théorie quantique à partir d'une idée extravagante est devenue l'un des modèles physiques les plus complets et les plus précis de notre Univers. Et enfin, pour ceux qui souhaitent approfondir le sujet, je voudrais recommander plusieurs ressources et livres:

• «Physique et philosophie» - Werner Heisenberg, compréhension de la théorie quantique, vue par l'un de ses fondateurs les plus éminents.
• QED - A Strange Theory of Light and Matter est un livre classique du brillant Richard Feynman, basé sur des conférences de vulgarisation scientifique qu'il a données dans les années 60 au California Institute of Technology (Caltech).
• « » — , , , — .
• « » — - , , .
• Physics Videos by Eugene Khutoryansky — YouTube , , , .
• Minute phisics — , , , : , , .
• 3Blue1Brown - Chaîne de Grant Sanderson, ancien élève d'Oxford, une excellente combinaison de présentation intelligible et de visualisation unique de concepts de: physique quantique , algèbre linéaire , réseaux de neurones . Grant est également l'auteur d'un cours sur le calcul multivarié disponible sur le site du projet à but non lucratif Khan Academy .