👨🏾‍🍳 🖐🏽 🏒 Problème de sac à dos en cryptographie 🕘 😡 🌒

Le problème Knapsack (problème Knapsack) en cryptographie est le problème sur la base duquel les cryptographes américains Ralph Merkle et Martin Hellman ont développé le premier algorithme de cryptage à clé publique.

Plus loin dans le programme

Formulation du problème du sac à dos (+ pourquoi un sac à dos?)
Des défis faciles et difficiles
Exemples de
Histoire

Qu'est-ce que le chiffrement à clé publique?

, , «», .

. , , , .

: , .

, - !

Le premier algorithme de clé publique générale a utilisé l'algorithme de sac à dos.

Sur la base de la définition des systèmes de clés publiques, il faut deux clés pour chiffrer (et déchiffrer) un message avec succès. Le destinataire "légal" du message connaît la clé secrète

А

tandis que l'expéditeur possède une autre clé publique

B

...

Que faire si une clé publique est connue d'un attaquant?

Il y a une réponse: la clé publique doit être obtenue à partir de la clé secrète à l'aide d'une transformation ( fonction unidirectionnelle )

f

avec les deux propriétés suivantes:

$B = f (A)$ connaissant A, il est facile de calculer la fonction elle-même

$A = f^{- 1} (B)$ , et il est difficile de calculer la fonction inverse

Qu'est-ce que «facile» et «difficile»?

.

«» , . ..

n

, —

t \propto n^{a}

a

— . , .

«» . , , .

..

n

t \propto 2 n

, , .

Le problème du sac à dos est formulé comme suit

L'ensemble (vecteur de sac à dos)

A = (a_{1}, . . ., a_{n})

Est un ensemble ordonné de

n

(

n > 2),

nombres naturels distincts

a_{i}

... Qu'il y ait un nombre

k

- ensemble et positif. La tâche est de trouver un tel ensemble

a_{i}

de sorte qu'au total, ils donnent exactement

k

...

Dans la version la plus connue du problème du sac à dos, il est nécessaire de savoir si une paire donnée a

(A, k)

décision. Dans la variante utilisée en cryptographie, vous avez besoin de cette entrée

(A, k)

construire une solution en sachant qu'une telle solution existe. Ces deux options sont NP-complètes.

Analogie avec le sac à dos

Dans le cas le plus simple

k

indique la taille (capacité) du sac à dos et chacun des nombres

a_{i}

indique la taille (poids) d'un article qui peut être emballé dans un sac à dos. La tâche est de trouver un tel ensemble d'articles afin que le

sac à dos soit complètement rempli.

Autrement dit, imaginez que vous avez un ensemble de poids 1, 6, 8, 15 et 24, vous devez emballer un sac à dos avec un poids de 30.

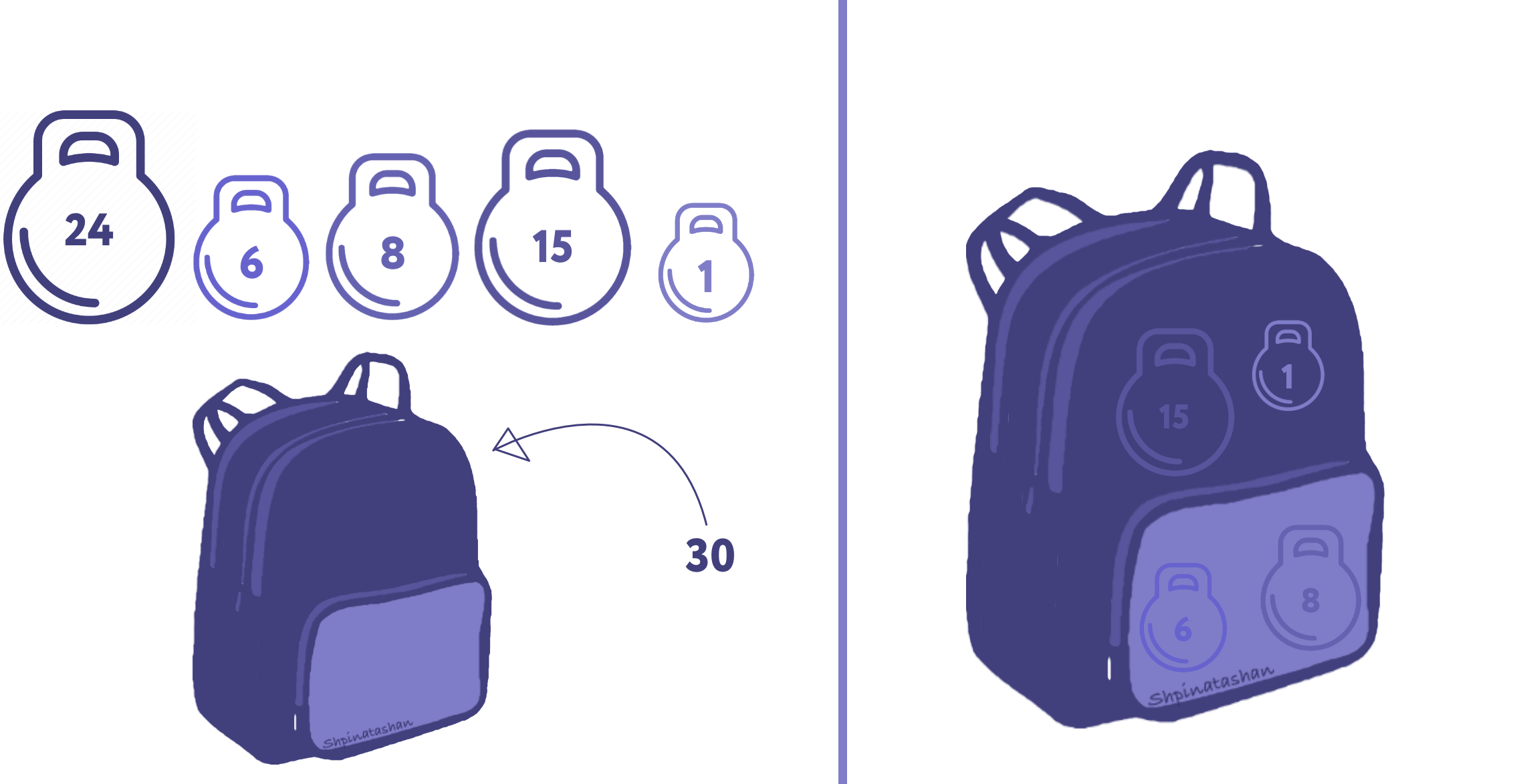
En principe, une solution peut toujours être trouvée par une recherche exhaustive de sous-ensembles

А

et vérifier laquelle de leurs sommes est

k

... Dans notre cas, cela signifie la force brute

2^{5} = 32

sous-ensembles (y compris l'ensemble vide). C'est tout à fait faisable.

Mais que faire s'il y a plusieurs centaines de numéros $a_{i}$ ?

Dans notre exemple, n = 5 pour ne pas compliquer la présentation. Dans des conditions réelles, un exemple aura, disons, 300

a_{i} - х

... Le point ici est qu'aucun algorithme n'est connu qui ait une complexité significativement inférieure par rapport à la recherche exhaustive. Rechercher parmi

2^{300}

les sous-ensembles ne peuvent pas être traités. En effet, le problème du sac à dos est connu sous le nom de NP-complet ... Les problèmes NP-complete sont considérés comme difficiles à calculer.

La fonction répond-elle aux exigences spécifiées?

Nous définissons la fonction

f (x)

de la manière suivante. N'importe quel chiffre

0 \leq x \leq 2 n - 1

peut être donnée par une représentation binaire de

n

bits, où des zéros non significatifs sont ajoutés si nécessaire. Maintenant définissons

f (x)

en nombre obtenu à partir de

A

résumer tout cela

a_{i}

que le bit correspondant en notation binaire

x

est égal à 1.

Autrement dit,

f (1) = f (0 . . . 001) = a_{n}

f (2) = f (0 . . . 010) = a_{n - 1}

f (3) = f (0 . . . 011) = a_{n - 1} + a_{n}

. . .

Fonction

f (х)

était déterminé

n -

ensemble

A

... Évidemment, si nous sommes capables de calculer

x

f (x)

, alors pratiquement en même temps le problème du sac à dos sera résolu:

x

sa représentation binaire est immédiatement calculée, ce qui donne à son tour les composantes de l'ensemble

A

inclus dans la somme pour

f (x)

... D'autre part, le calcul

f (x)

x

est léger. Puisque le problème du sac à dos est NP-complet,

f (x)

est un bon candidat pour une fonction unidirectionnelle. Bien sûr, il faut exiger que $n$ était assez grand, disons pas moins $200$ ...

Chiffrement

Texte brut

(. plain text) — , , . ( ).

Il existe deux façons de chiffrer:

Le chiffrement du message est obtenu en élevant les éléments de ce vecteur de sac à dos à la puissance des bits correspondants du message chiffré puis en multipliant tous les résultats, c'est-à-dire si $A = (2, 3, 5)$ et le message $(100)$ , alors le chiffre sera le nombre $2^{1} * 3^{0} * 5^{0} = 2$ . .
, , $A = (2, 3, 5)$ , $(100)$ , $2^{*} 1 + 3^{*} 0 + 5^{*} 0 = 2$ . .

Exemple

Pour crypter du texte brut en représentation binaire, il est divisé en blocs de longueur

n

(par exemple, vous pouvez représenter le poids 30 avec le binaire 11110). On pense que l'un indique la présence d'un objet dans le sac à dos, et zéro indique son absence.

Le chiffrement à dos offre une bonne approche pour créer des clés publiques et privées, où la clé privée est facile à utiliser et la clé publique est difficile à comprendre.

Ainsi, nous pouvons créer un système où: le problème "dur" est la

clé publique , car avec lui, vous pouvez facilement crypter et il est impossible de décrypter le message.

une clé privée - le problème "facile" servira de en l'utilisant, vous pouvez facilement décrypter le message. Sans la clé privée, vous devez résoudre le problème "difficile" du sac à dos.

Problème "facile"

Vecteur de sac à dos super croissant

A = (a_{1}, . . ., a_{n})

Σ_{i = 1}^{j - 1} a_{i} < a_{j}

j = 2, . . ., n

, . .

Pour les vecteurs super-croissants Α, le problème du sac à dos est facilement résoluble. Ceux. le sac à dos est facile à assembler.

Prenons un exemple:

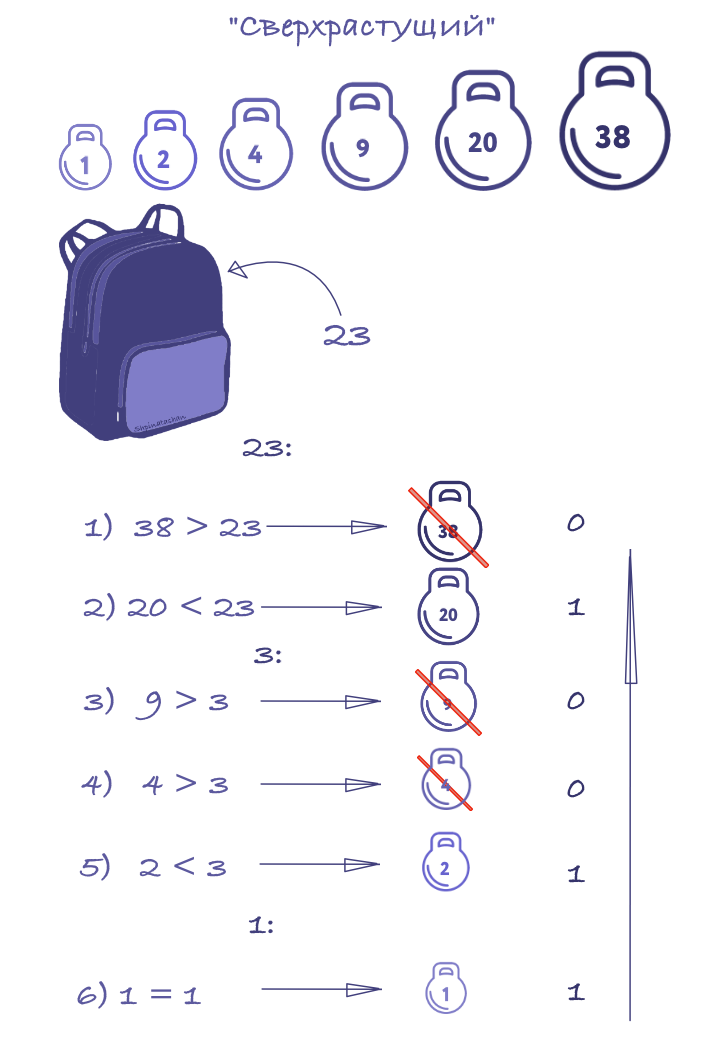
Algorithme

.

, , . , .
.
(1)-(2) .

, .

"Problème difficile

Il est beaucoup plus difficile de déchiffrer le problème d'un sac à dos non surdimensionné .

Un algorithme, qui utilise un sac à dos à clé privée surdimensionné et un sac à dos à clé publique non surdimensionné, a été créé par Merkle et Hellman.

Ils l'ont fait en prenant la tâche du sac à dos surdimensionné et en la transformant en une tâche non surdimensionnée.

(Merkle et Hellman, en utilisant l'arithmétique modulaire, ont conçu un moyen de transformer un sac à dos "léger" en un sac à dos "dur")

Créer une clé publique

Plusieurs concepts importants

$(x, m o d m)$ $x$ $m$ ,

$x$ — , $m > 1$ , [x/m] — ,
$x = (x, m o d m) + [x / m] * m$

$A$ , $m > m a x A$ $t < m$ , $(t, m) = 1$ .

$B = (b_{1}, . . ., b_{n})$ , $b_{i} = (t a_{i}, m o d m)$ , $i = 1, . . ., n$ , , B A m t , , $(m, t)$ .

$(t, m) = 1$

$t^{- 1} = u$ , ,

$t u \equiv 1 (m o d m)$

$1 \leq u < m$ . , $A$ $B$

$m, u$ .

$m > m a x A$

$m > Σ_{i = 1}^{n} a_{i}$ , , $B$ $A$ $m, t$ .

— , , , .

Le créateur du cryptosystème choisit un tel système

A, t, m, B

ce vecteur

A

est en pleine croissance, et

B

vient de

A

forte multiplication modulaire par rapport à

m, t

... Vecteur

B

étendu en tant que clé de cryptage et blocs binaires de longueur

n

envoyé au concepteur sous forme de nombres

β

obtenu en utilisant le vecteur

B

...

L'intercepteur de messages doit résoudre le problème du sac à dos pour entrer

(B, β)

... Le créateur du cryptosystème calcule

α = (u β, m o d m)

et résout le problème d'entrée du sac à dos

(A, α)

... Pourquoi tout cela fonctionne est

montré dans le lemme suivant.

Lemme . Faisons semblant que

A = (a_{1}, . . ., a_{n})

super vecteur et vecteur de croissance

B

dérivé de

A

forte multiplication modulaire par rapport à

m, t

... Supposons en outre que

u \equiv t^{- 1} (m o d m)

β

- un nombre naturel arbitraire et

α = (u β, m o d m)

... Alors les affirmations suivantes sont vraies.

(i) Le problème du sac à dos

(A, α)

résoluble en temps linéaire. Si une solution existe, elle est unique.

(ii) Le problème du sac à dos

(B, β)

a au plus une solution.

(iii) S'il y a une solution à saisir

(B, β)

, alors il correspond à la seule solution d'entrée

(A, α)

...

preuve (p. 104)

Exemple

Considérons une séquence super-croissante; par exemple, {1, 2, 4, 10, 20, 40}. Le module doit être supérieur à la somme de tous les nombres de la séquence, par exemple 110. Le multiplicateur ne doit pas avoir de diviseurs communs avec le module. Alors choisissons 31.

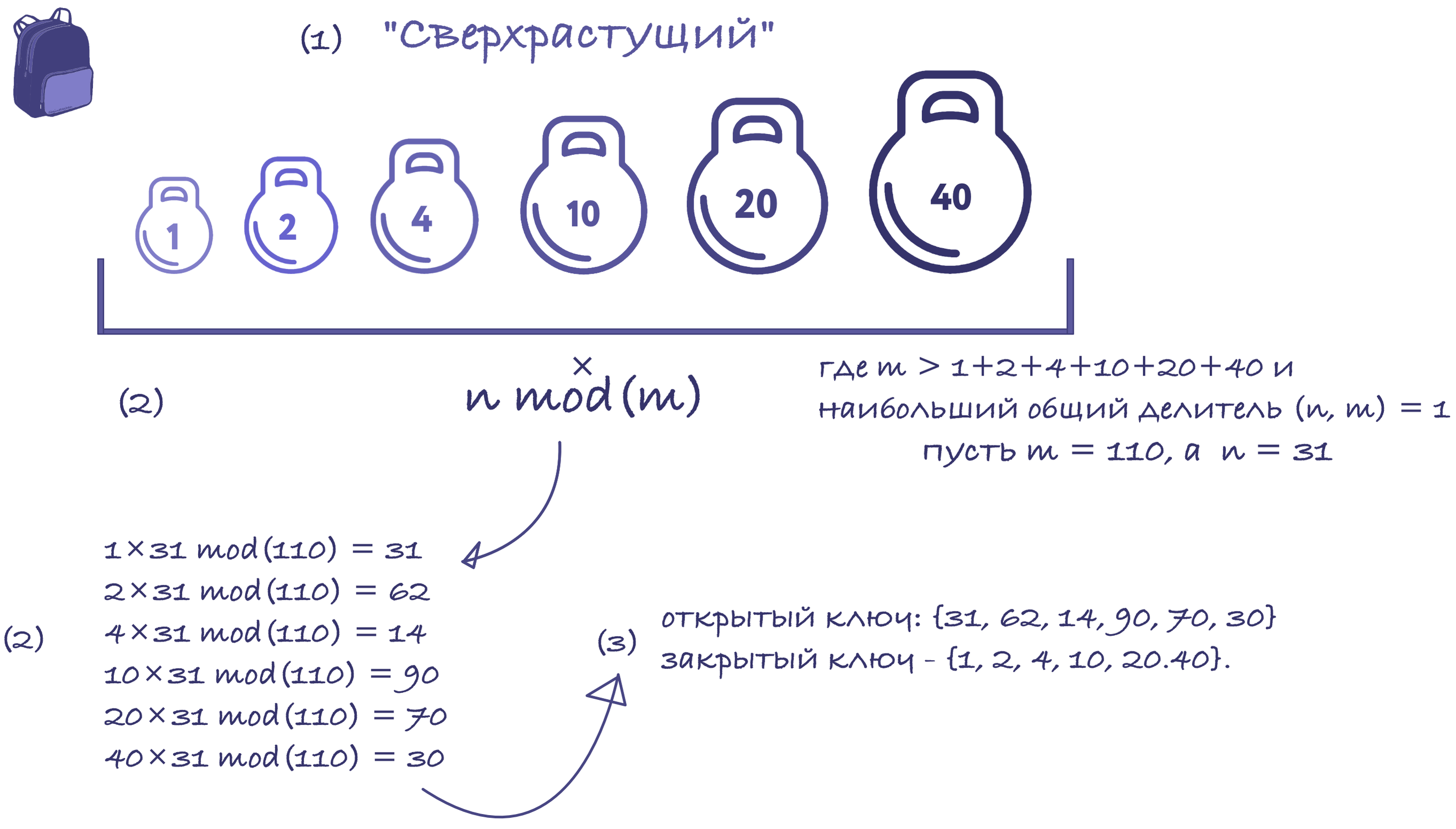
Nous avons donc calculé la clé publique: {31, 62, 14, 90, 70, 30} et la clé privée - {1, 2, 4, 10, 20,40}.

Essayons maintenant d'envoyer une séquence binaire: 100100111100101110

Certains des avantages des clés publiques

. , , . , , . ( )

Pendant longtemps, les cryptosystèmes à dos ont été considérés comme les cryptosystèmes les plus attractifs et les plus prometteurs en raison de leur exhaustivité NP et de leur vitesse de cryptage et de décryptage élevée. De nombreux schémas utilisent le problème du sac à dos (dans diverses variantes), en voici quelques-uns: le problème du sac à dos compact, le problème du sac à dos multiplicatif, le problème du sac à dos modulaire, le problème de la couverture matricielle, le problème de la factorisation de groupe ...

Malheureusement, la plupart d'entre eux sont vulnérables à attaques. Il s'est avéré qu'il n'est pas anodin de concevoir un cryptosystème sécurisé basé sur le problème du sac à dos, bien que le problème soit connu sous le nom de NP-complete. La plupart des cryptosystèmes à dos ont été piratés. Malgré cela, contrairement à la factorisation entière et au logarithme discret, le problème général du sac à dos (solution) est un problème NP-complet prouvé.

Certaines personnes pensent qu'un jour un algorithme polynomial-temps pourrait être inventé pour résoudre des problèmes de factorisation d'entiers et de logarithmes discrets, alors que le problème du sac à dos est toujours NP-complet.

Il y a plusieurs "MAIS" ici.

Premièrement, l'exhaustivité NP est basée sur l'analyse du cas le plus défavorable; deuxièmement, l'exhaustivité NP est une caractéristique d'un problème général et non d'un cas particulier. Cela signifie que si l'on considère la complexité moyenne, le problème du sac à dos peut être facile.

Le matériel a été préparé sur la base de cette littérature:

(1) A. Salomaa. Cryptographie à clé publique. - Springer-Verlag, 1990. - p. 75-82, pages 101-111

(2)Min Kin Lai. Knapsack Cryptosystems : Past and Future - Université de Californie, 2001

(3) Baocang Wang, Qianhong Wu, Yupu Hu. Un schéma de cryptage probabiliste basé sur un sac à dos. 2007

(4) - (5)

Problème de sac à dos en cryptographie