Détection d'anomalies à l'aide de techniques d'apprentissage en profondeur
Identifier les anomalies (ou valeurs aberrantes) dans les données est un défi pour les scientifiques et les ingénieurs de divers domaines de la science et de la technologie. Bien que la détection d'anomalies (objets qui ne ressemblent pas à l'ensemble de données principal) ait été traitée pendant longtemps et que les premiers algorithmes aient été développés dans les années 60 du siècle dernier, dans ce domaine, il existe de nombreux problèmes non résolus et des problèmes auxquels les gens sont confrontés dans des domaines tels que conseil, scoring bancaire, sécurité de l'information, transactions financières et santé. Dans le cadre du développement rapide des algorithmes d'apprentissage en profondeur au cours des dernières années, de nombreuses approches modernes pour résoudre ce problème ont été proposées pour différents types de données étudiées, qu'il s'agisse d'images, d'enregistrements de caméras de vidéosurveillance, de données tabulaires (sur les transactions financières), etc.
- Deep Anomaly Detection (DAD) - :
: . . - , ,
:
:
: , , , ( - )
:
precision / ( )
[2] G. Pang .
:
Deep learning for feature extraction - , ( ), . DAD.
.2 . φ(·) : X→ Z Z, .
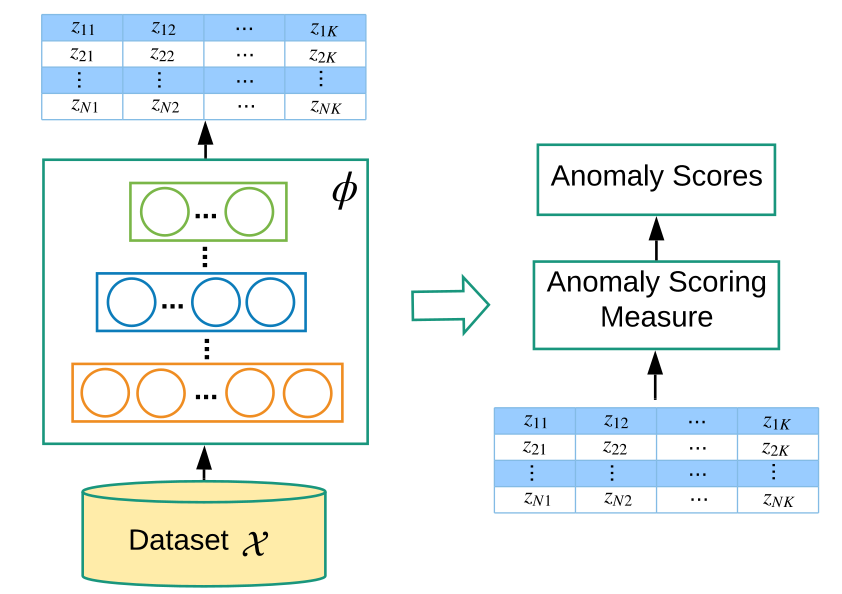
Learning feature representation of normality - φ(·) : X→ Z , , Z .
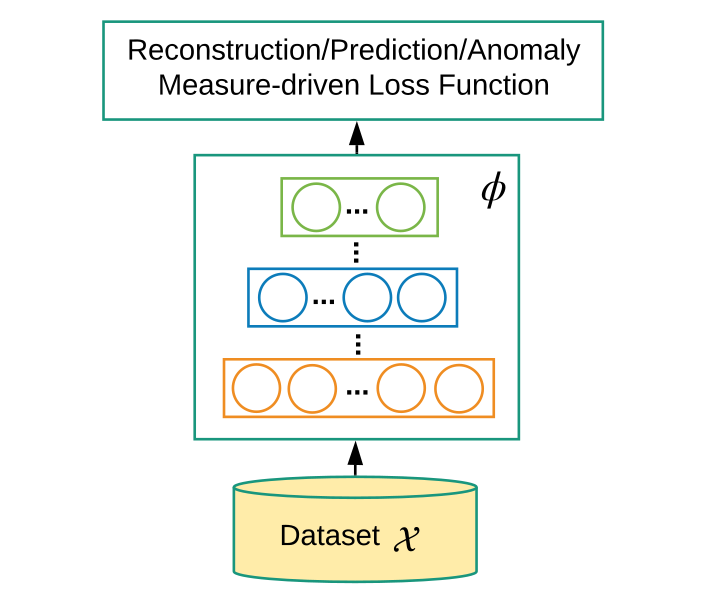
End-to-end anomaly score learning - end-to-end , anomaly score.
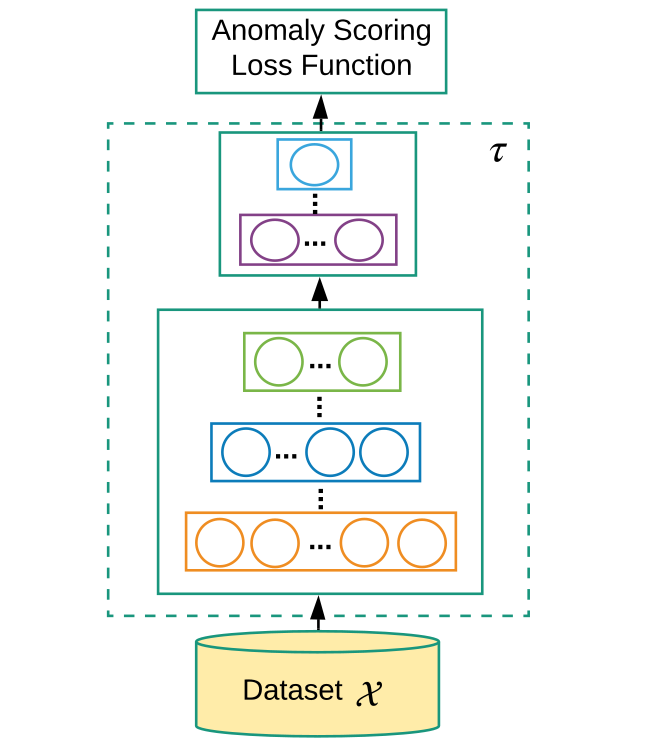
, .
Deep learning for feature extraction
. , PCA (principal component analysis) [3] random projection [4], , . MLP, , NNs , RNNs ().
, anomaly score .
Learning feature representation of normality
.1 .
Generic Normality Feature Learning. . , .
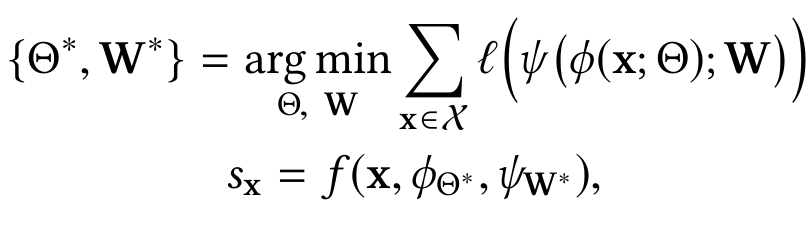
ψ - , l - , ψ, φ ( ), f - .
:
DAD , , . [5]
- , , , .
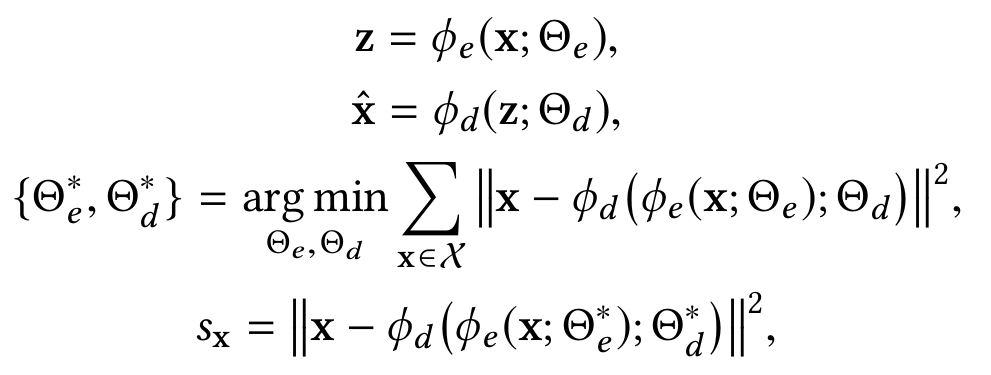
φ_e (.) - , , φ_d (.) - , . s_x (data reconstruction error) .
Generative Adversarial Networks
GANs - , , ( G) , ( D) .
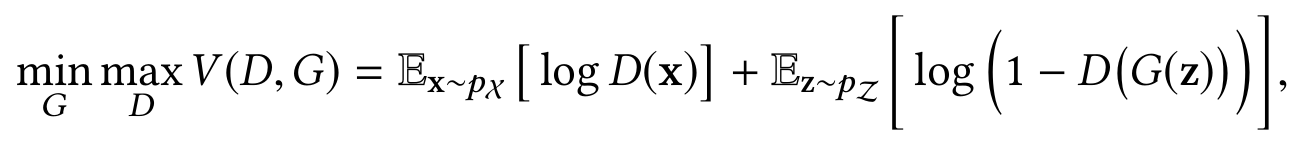
G D - .
DAD , . , , . AnoGAN [6].
Predictability Modeling. .

x̂_(t +1) = ψ (φ (x1 , x2 , · · · , xt ; Θ); W),
l_pred l_adv - , .
, , . . [7]
Self-supervised Classification. , ( - (n - 1) , - , ). . , .
Anomaly Measure-dependent Feature Learning.
φ(·) : X→ Z, .
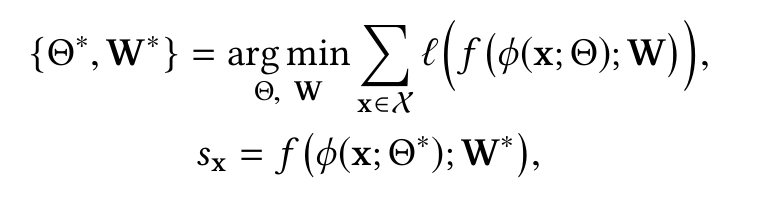
l - .
:
Distance-based Measure. , : DB outliers [8], k-nearest neighbor distance [9] . - , .
One-class Classification-based Measure. , , , . one-class SVM [10], Support Vector Data Description (SVDD) [11].
Clustering-based Measure. , , [12].
End-to-end anomaly score learning
, anomaly score.
:
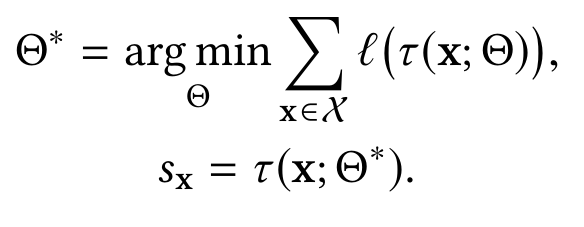
τ (x; Θ) : X→ R , .
Ranking Models. end-to-end . , . Self-trained deep ordinal regression model [13].
Prior-driven Models. - the Bayesian inverse RL-based sequential anomaly detection. - , . [14].
Softmax Models. , . , .
Deviation Networks (end-to-end pipeline) [1]
, G. Pang , . .5 .
function φ - anomaly scoring network, . Reference score generator - , ( ). ( φ(x; Θ) μ_R) deviation loss function L, anomaly scoring network , , .
deviation loss function
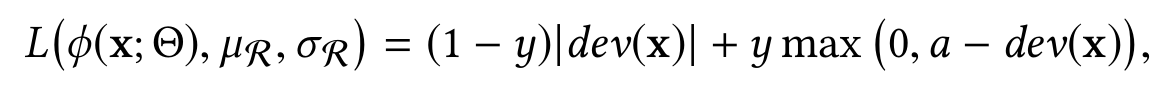

y = 1, , y = 0 . , anomaly score , φ(x; Θ), dev(x) , , "a" ( ). .
, , . SOTA-. end-to-end .
[1] Deep Anomaly Detection with Deviation Networks. G. Pang
[2] Deep Learning for Anomaly Detection: A Review. G. Pang
[3] Emmanuel J Candès, Xiaodong Li, Yi Ma, and John Wright. 2011. Robust principal component analysis?
[4] Ping Li, Trevor J Hastie, and Kenneth W Church. 2006. Very sparse random projections.
[5] Alireza Makhzani and Brendan Frey. 2014. K-sparse autoencoders. In ICLR.
[6] Thomas Schlegl, Philipp Seeböck, Sebastian M Waldstein, Ursula Schmidt-Erfurth, and Georg Langs. 2017. Unsupervised anomaly detection with generative adversarial networks to guide marker discovery.
[7] Wen Liu, Weixin Luo, Dongze Lian, and Shenghua Gao. 2018. Future frame prediction for anomaly detection–a new baseline.
[8] Edwin M Knorr and Raymond T Ng. 1999. Finding intensional knowledge of distance-based outliers.[9] Fabrizio Angiulli and Clara Pizzuti. 2002. Fast outlier detection in high dimensional spaces.
[10] Bernhard Schölkopf, John C Platt, John Shawe-Taylor, Alex J Smola, and Robert C Williamson. 2001. Estimating the support of a high-dimensional distribution.
[11] David MJ Tax and Robert PW Duin. 2004. Support vector data description.
[12] Mathilde Caron, Piotr Bojanowski, Armand Joulin, and Matthijs Douze. 2018. Deep clustering for unsupervised learning of visual features.
[13] Guansong Pang, Cheng Yan, Chunhua Shen, Anton van den Hengel, and Xiao Bai. 2020. Self-trained Deep Ordinal Regression for End-to-End Video Anomaly Detection.
[14] Andrew Y Ng et Stuart J Russell. 2000. Algorithmes pour l'apprentissage par renforcement inverse.