Cet article décrit en termes simples les cryptoalgorithmes qui sont actuellement des normes de sécurité de l'information russes pertinentes, et des liens sélectionnés vers des matériaux qui, si vous le souhaitez, aideront à les comprendre plus en profondeur. Et aussi, à la fin de l'article, des travaux avec les résultats de la cryptanalyse de l'un des éléments les plus importants de ces algorithmes sont donnés.
Des actualités
. , .

2020 « — , », . , . , 2024 , .
, - eSim.
, .
, .
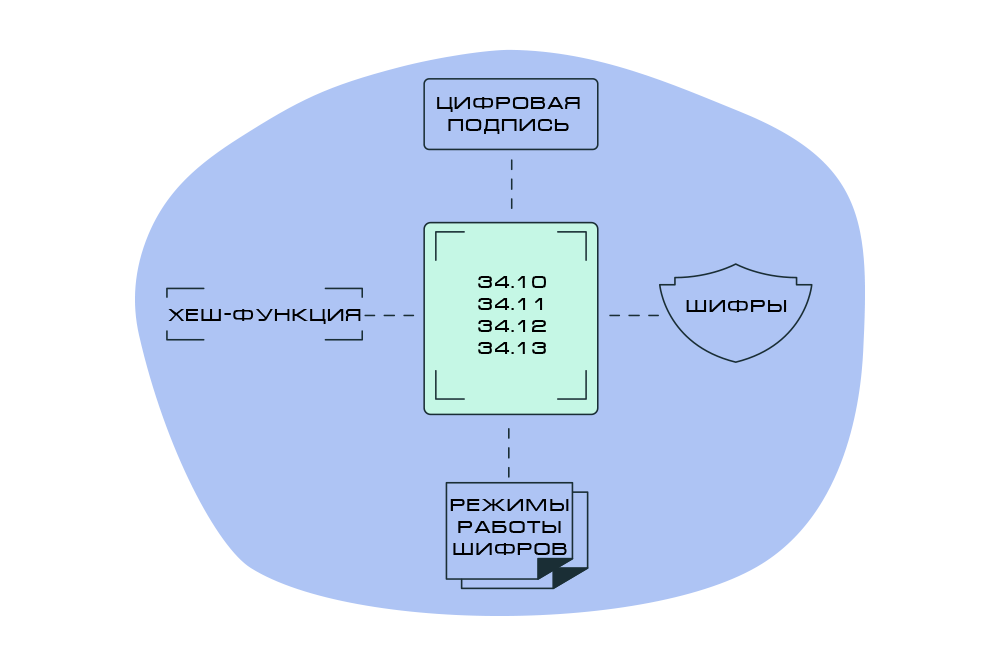
34.10-2018 . 256 512 .
, . , , . , , , .
, , , .
,
,
,
, ( )
,
,
.
, . .
,
, ,
,
,
.
,
.
, , .
.
.

:
.
— -() - , , - — .
— ,
— , -
.
,
1.
— , .
— .
— , .
.
.
— ,
.
,
0, .
: .
.
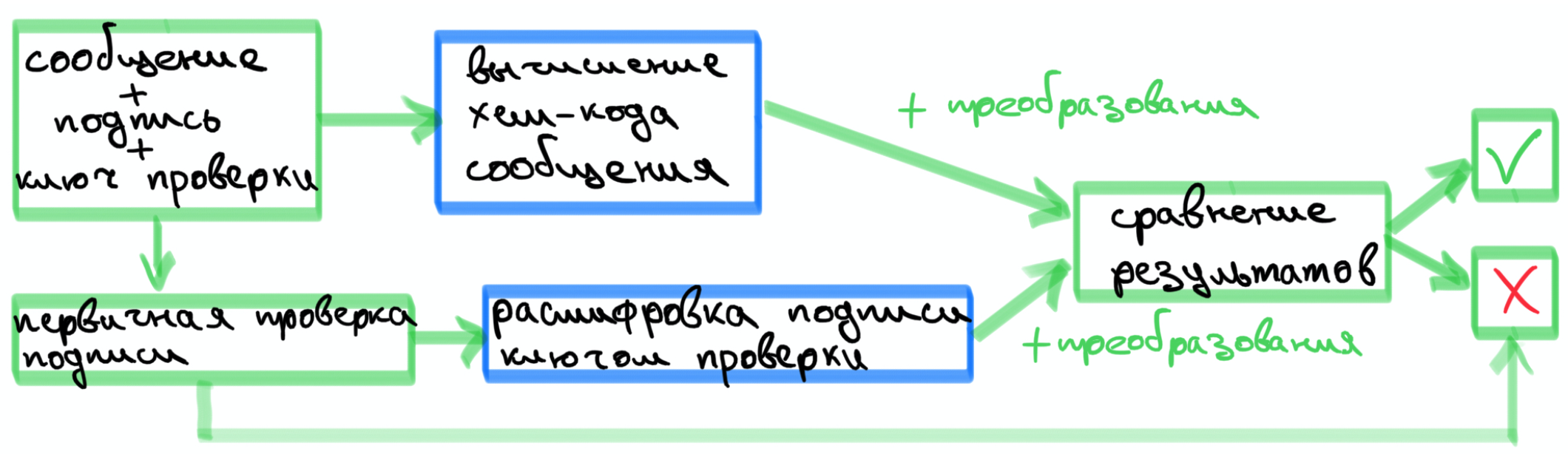
: c
— , , , .
— - , .
— ,
, -
.
,
1.
.
— ,
.
— ,
: /
-
34.11-2018 . -, , .
, 512 ( ). - 256 512 .
@NeverWalkAloner.
34.12-2018 . — 128 64 256 .
10 , , ( ).
.

, , .
@sevastyan01 .
32 , , .
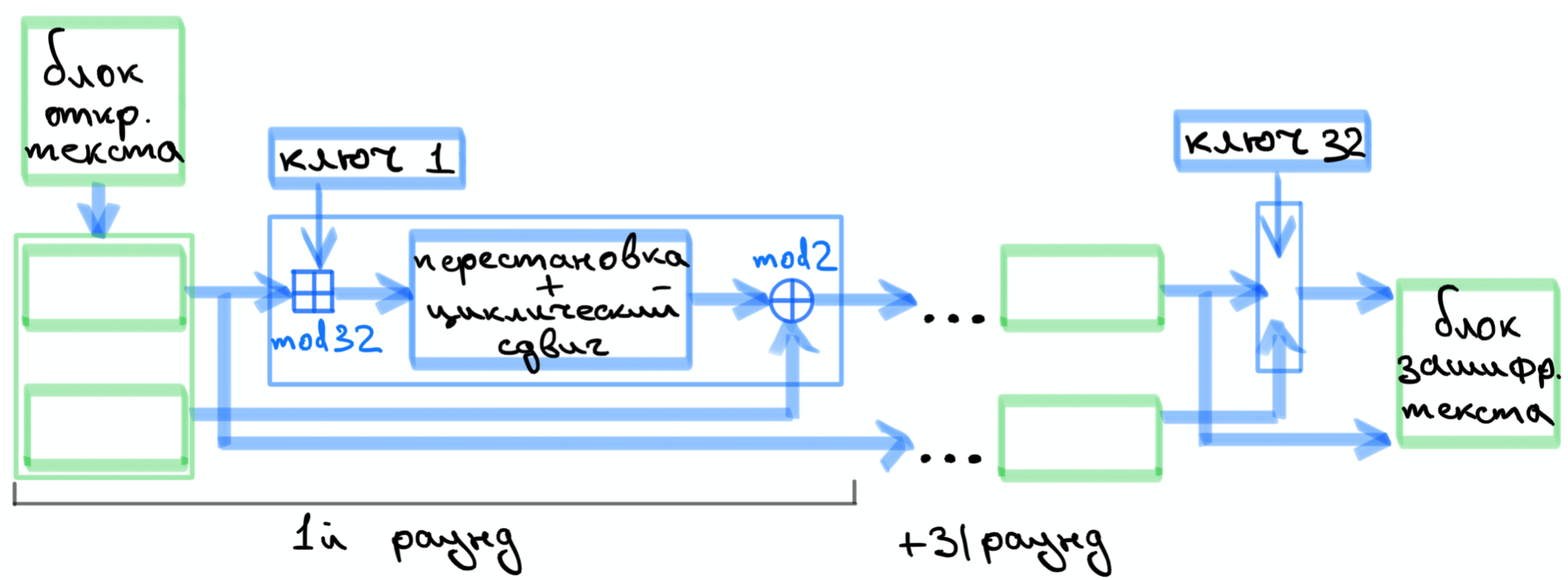
, .
34.13-2018 .
. , , . , .

. , .

2, XOR. , , .
, .
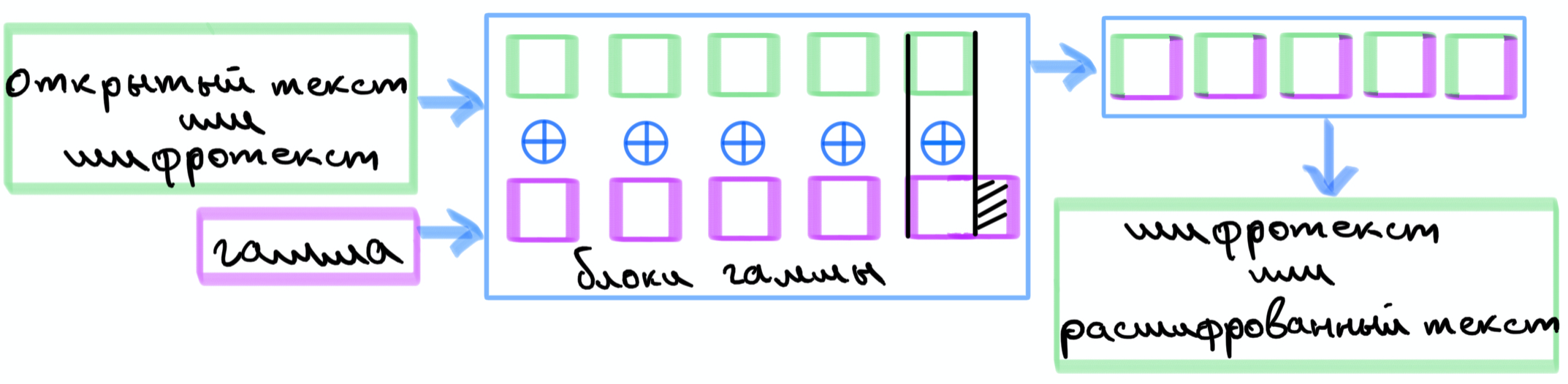
, . .
: ,
, . , , .
.

. , , . .
, , , .
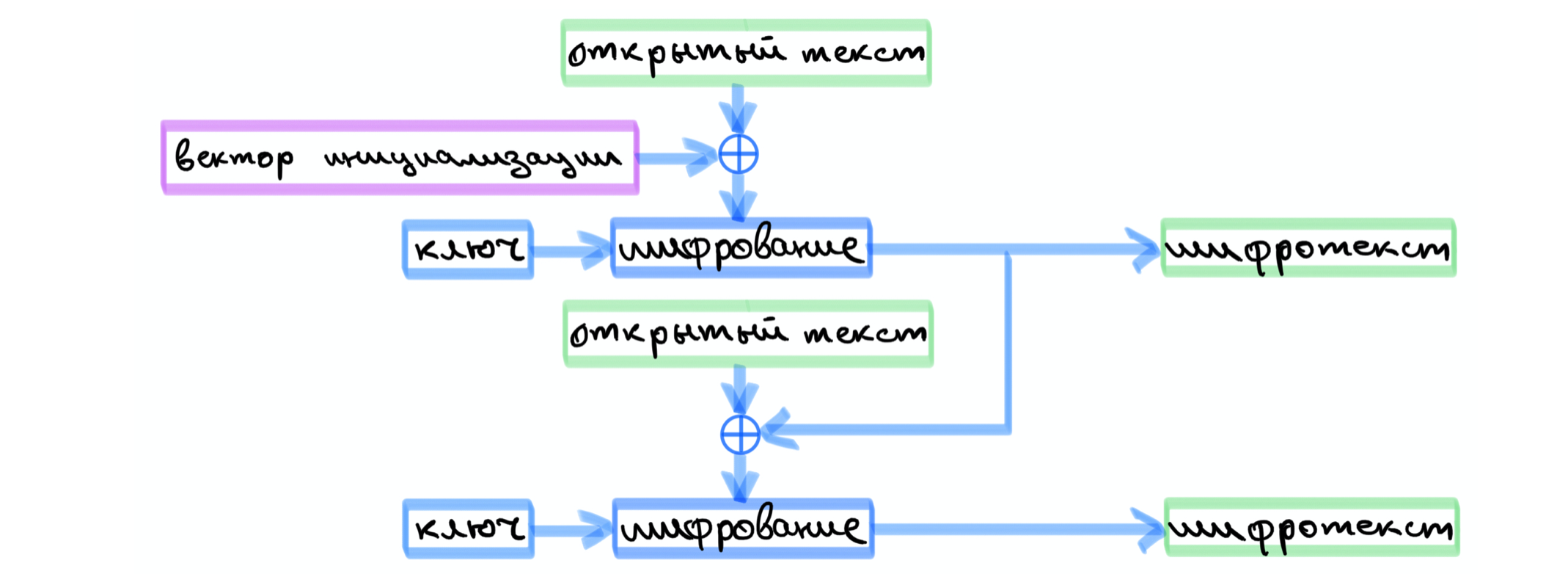
, .
1 2019 . , .
@ru_crypt .
34.10-2018. - , 34.11-2018.
34.12-2018.
. 34.11-2018, .
, . .
, . , .
:
Reverse-Engineering the S-Box of Streebog, Kuznyechik and STRIBOBr1 — Alex Biryukov, L ́eo Perrin, and Aleksei Udovenko
Exponential S-Boxes: a Link Between the S-Boxes of BelT and Kuznyechik/Streebog — Léo Perrin and Aleksei Udovenko
Partitions in the S-Box of Streebog and Kuznyechik — Léo Perrin
, SageMath.
, . , .