«J'ai récemment commencé à expérimenter avec gnuplot et j'ai rapidement fait une découverte intéressante. J'ai tracé tous les nombres premiers inférieurs à 1 million en coordonnées polaires, donc pour chaque premier p (r, θ) = (p, p). Je ne m'attendais à rien de spécial, j'ai juste essayé. Les résultats sont impressionnants. "
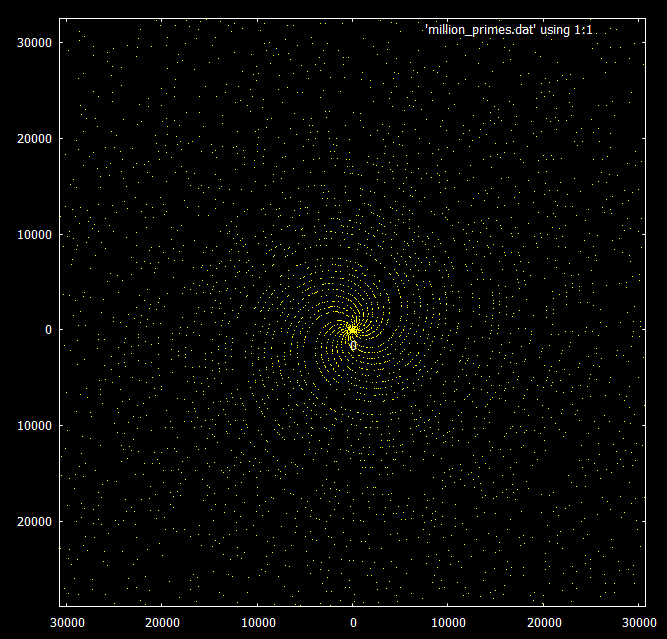
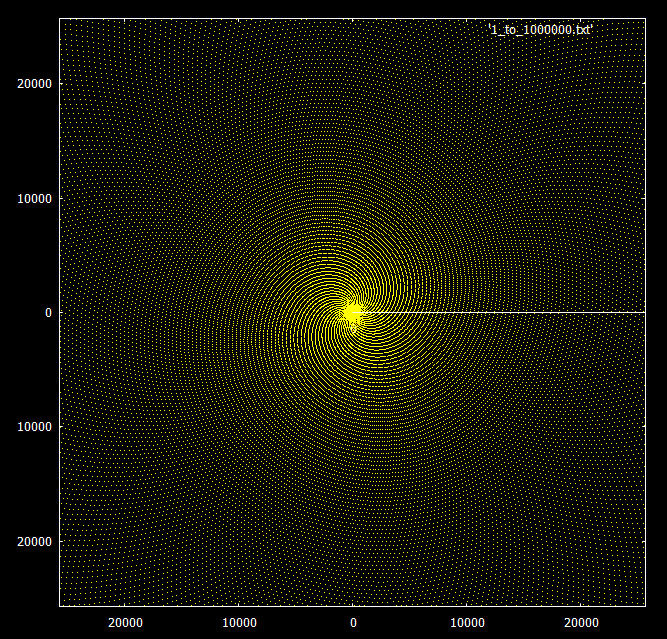
Si vous regardez les nombres premiers inférieurs à 30 000, vous pouvez voir un modèle en spirale.
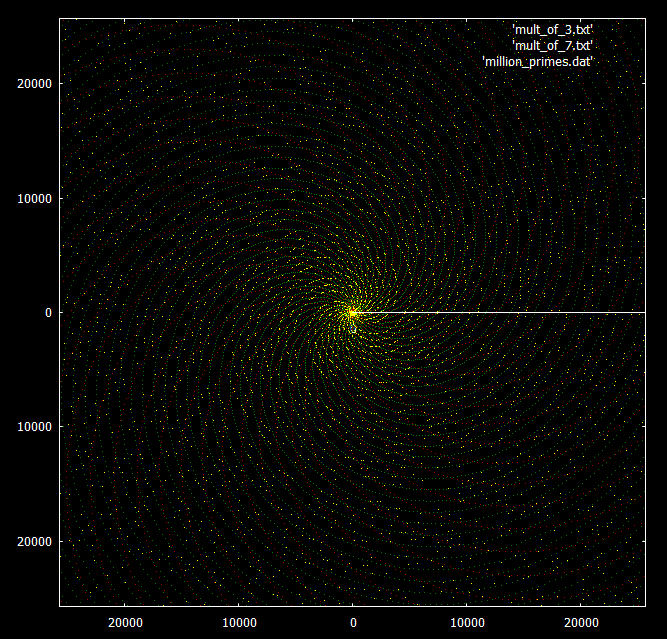
À titre de comparaison - le même graphique avec des nombres superposés en multiples de 3 et 7. Les nombres premiers sont surlignés en jaune, les multiples de 3 et 7 en vert et rouge, respectivement.

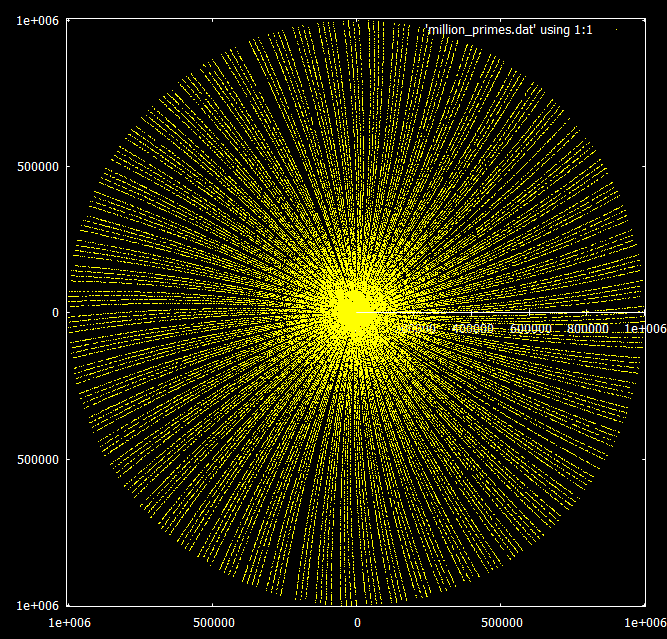
Ce qui est vraiment intéressant, c'est le comportement lors de l'augmentation de la portée. Les multiples de ce nombre semblent tourner en spirale dans le même modèle à l'infini, mais les nombres premiers commencent à former des rayons par groupes de 3 ou 4.
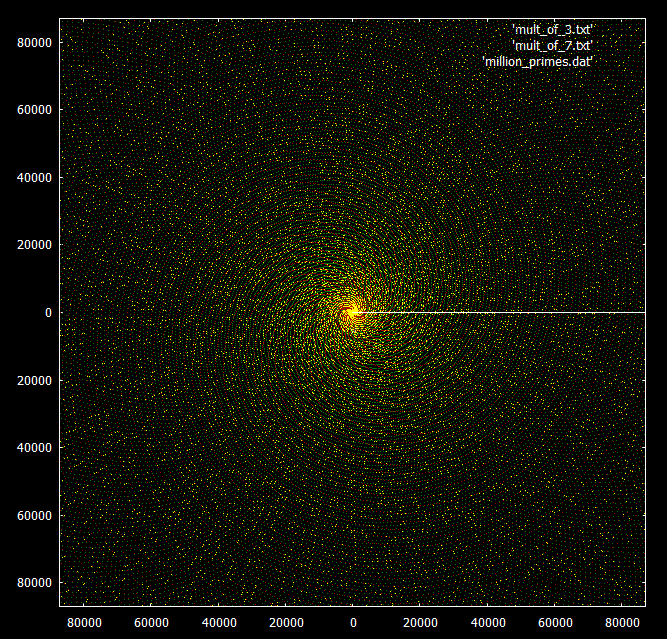
Par rapport aux multiples de 3 et 7:
? , ?
. , , .
(, θ) = (n, n), n∈N
Pour commencer, vous pouvez jouer avec les coordonnées polaires et considérer tous les points avec des coordonnées entières: (1,1) (2,2) ...
Nous
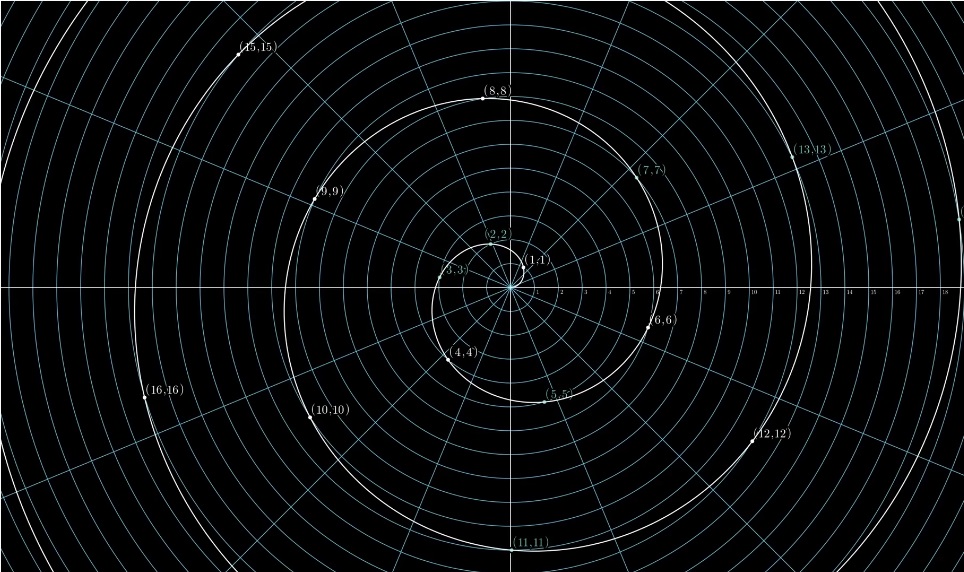
obtenons la spirale d'Archimède: Si nous excluons tous les nombres sauf les nombres premiers, nous obtenons une galaxie spirale avec des espaces:
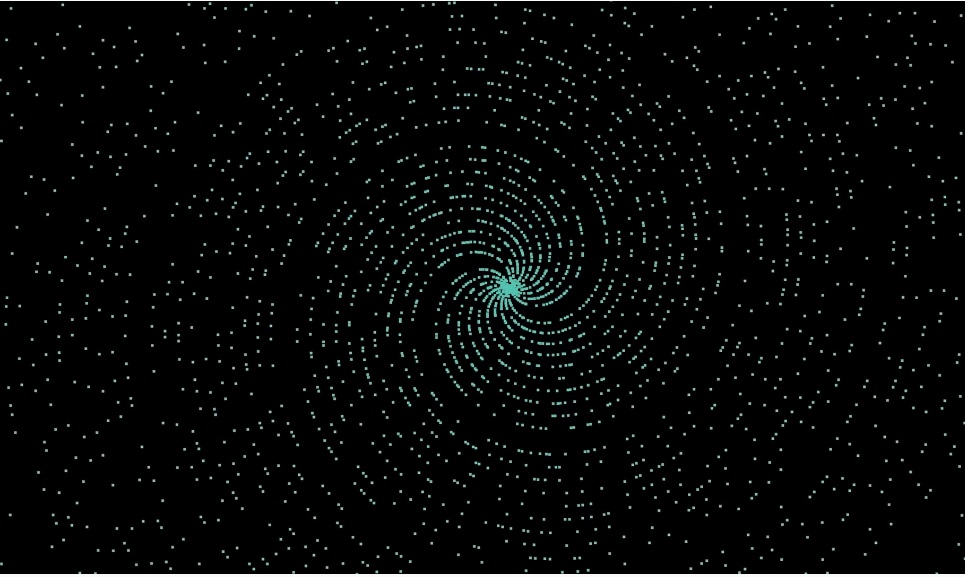
"En s'éloignant" on peut pour voir les rayons dirigés dans toutes les directions, principalement par groupes de 4: Les

spirales peuvent être comptées, il y en a 20:

Et les rayons 280:

Si nous prenons tous les nombres, pas seulement les simples, alors les spirales sont encore plus égales et il y en a 44:

À y regarder de plus près, nous avons 6 spirales:

Tous les nombres multiples de 6 forment une branche:
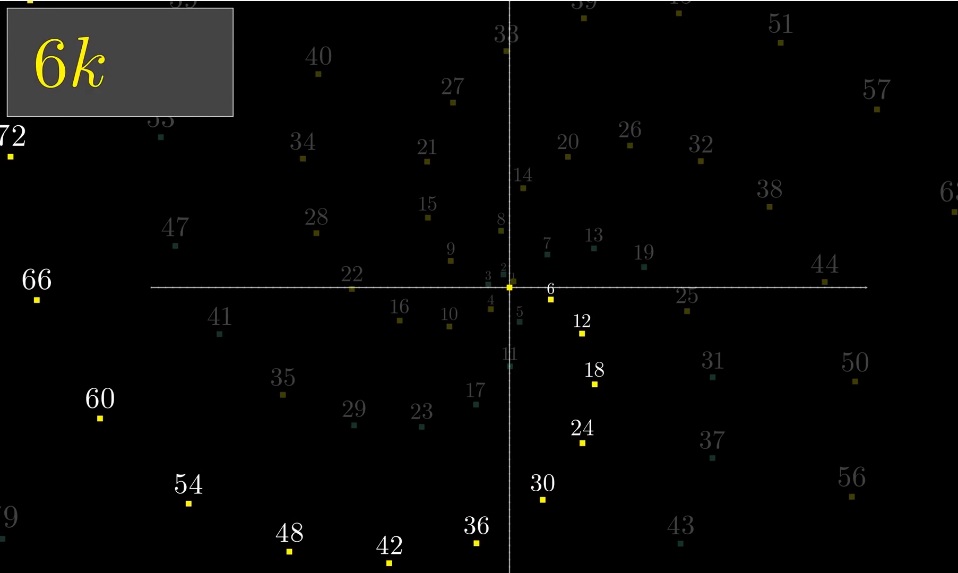
Le reste des bras en spirale est 6k + 1, 6k + 2, etc. Pourquoi donc? Parce que 6 est à peu près égal à (tour complet) 2ℼ (6,28318530718). Cette petite différence crée l'illusion d'une seule courbe.
Si vous ne laissez que les nombres premiers, il n'y aura que deux spirales (6k + 1 et 6k + 5):
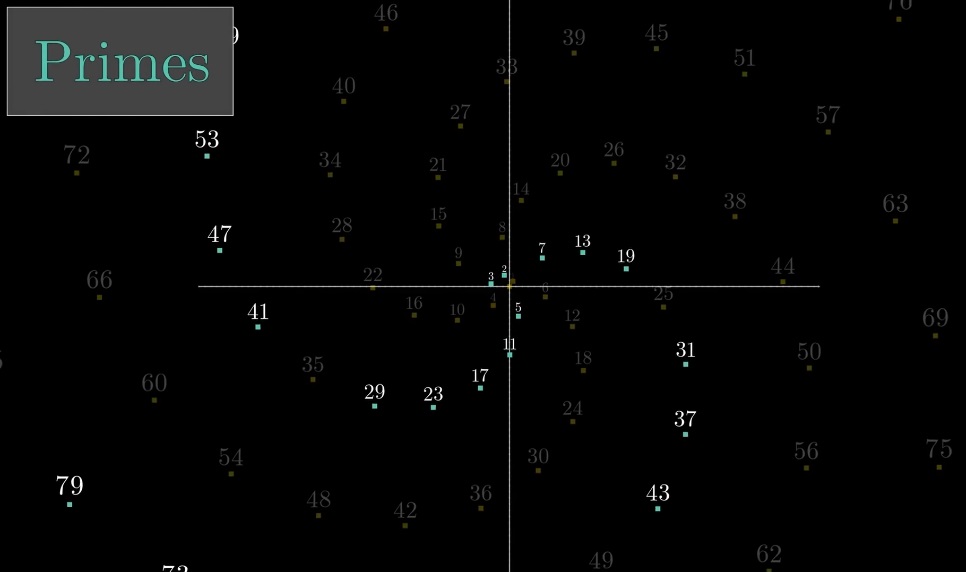
6 - presque un cercle complet, 44 - une approximation encore plus précise (44 / 2ℼ ≈ 7 cercles complets)
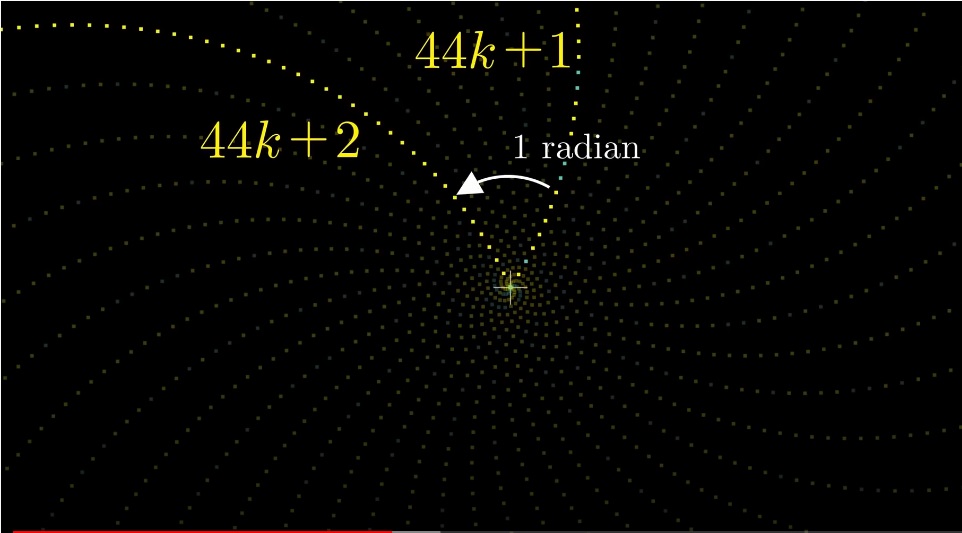
Seulement pour les nombres premiers, il y a 20 manches (44k +1, 44k + 3, 44k + 5 ...). Fonction d'Euler φ (44) = 20.

710 / 2ℼ ≈ 113. (113.00000959)

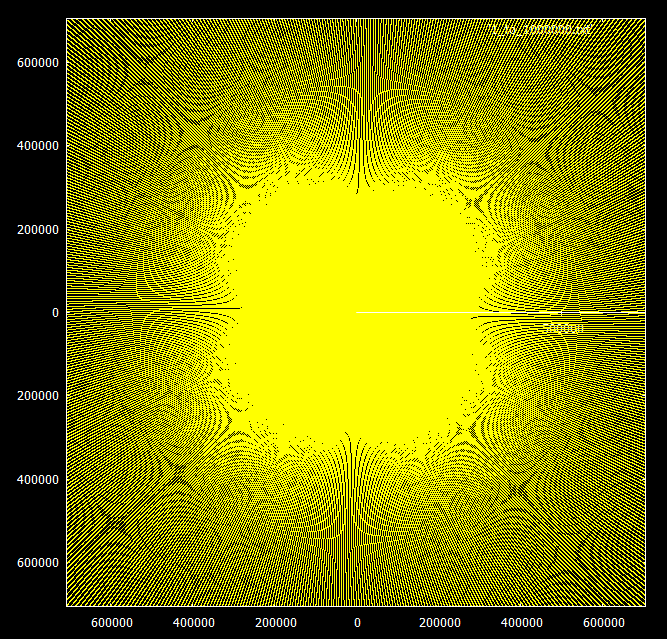
Pour les nombres premiers, il y aura des lacunes:

plus on s'éloigne, plus la courbure de toute la structure apparaît clairement.
710 = 71 * 5 * 2. Ceci explique le regroupement de 4 poutres (5) et les «dents cassées du peigne» (71):

fonction d'Euler φ (710) = 280.
D'après le théorème de Dirichlet, les nombres premiers sont uniformément répartis sur les manchons.
Conclusion
En jouant avec la visualisation, on peut tomber sur a) le principe de Dirichlet b) approcher le nombre ℼ (et les fractions continues) c) atteindre la fonction d'Euler.
La forme en spirale est un artefact associé à un nombre pair de radians correspondant.
Film avec doublage russe:
PS
Plus de travail sur les nombres premiers:
- Espaces limités entre les nombres premiers . (Par Yitang Zhang, 2014)
- Primes in tuples I (Par DANIEL A. GOLDSTON, JÁNOS PINTZ et CEM Y. YILDIRIM, 2009)
Fractions continues de Savvateev:
Alexey Savvateev "Tout sur l'écriture des nombres":