
Alors, considérons un graphique pondéré dirigé. Laissez le graphe avoir n sommets. Chaque paire de sommets correspond à un poids (probabilité de transition).

Il convient de noter que les graphiques Web typiques sont une chaîne de Markov discrète homogène pour laquelle la condition d'indécomposabilité et la condition d'apériodicité sont satisfaites.
Écrivons l'équation de Kolmogorov-Chapman:
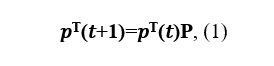
où P est la matrice de transition.
Supposons qu'il y ait une limite: le
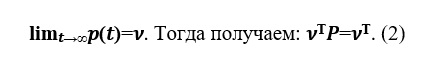
vecteur v est appelé une distribution de probabilité stationnaire.
C'est à partir de la relation (2) qu'il a été proposé de rechercher le vecteur de classement des pages Web dans le modèle Brin-Page.
Puisque v est une limite,

la distribution stationnaire peut être calculée par la méthode des itérations simples (MPI).
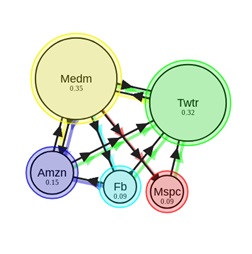
Pour passer d'une page Web à une autre, l'utilisateur doit, avec une certaine probabilité, choisir le lien vers lequel se rendre. Si le document comporte plusieurs liens sortants, nous supposerons que l'utilisateur clique sur chacun d'eux avec la même probabilité. Et enfin, il y a aussi le coefficient de téléportation, qui nous montre qu'avec une certaine probabilité l'utilisateur peut passer du document courant à une autre page, pas nécessairement directement liée à la page dans laquelle nous nous trouvons en ce moment. Laissez l'utilisateur se téléporter avec une probabilité δ, alors l'équation (1) prendra la forme

Pour 0 <δ <1, l'équation est garantie d'avoir une solution unique. En pratique, une équation avec δ = 0,15 est généralement utilisée pour calculer le PageRank.
Prenons un graphique Web Google à partir d'un lien de site. Ce graphique Web contient 875713 sommets, ce qui signifie que pour une matrice bidimensionnelle P, vous devez allouer 714 Go de mémoire. La RAM des ordinateurs modernes est d'un ordre de grandeur en moins, de sorte que l'ordinateur commence à utiliser la mémoire du disque dur, dont l'accès ralentit considérablement le travail du programme de calcul du PageRank. Mais la matrice P est une matrice creuse - une matrice avec essentiellement zéro élément. Pour travailler avec des matrices creuses en Python, le module sparse de la bibliothèque scipy est utilisé, ce qui aide la matrice P à prendre beaucoup moins de mémoire.
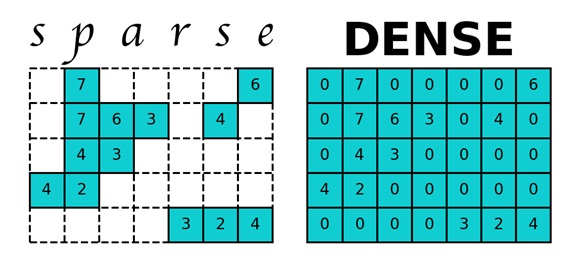
Appliquons cet algorithme à ces données. Les nœuds sont des pages Web et les bords dirigés sont des hyperliens entre eux.
Tout d'abord, importons les bibliothèques dont nous avons besoin:
import cvxpy as cp
import numpy as np
import pandas as pd
import time
import numpy.linalg as ln
from scipy.sparse import csr_matrix
Passons maintenant à l'implémentation elle-même:
#
data = pd.read_csv("web-Google.txt", names = ['i','j'], sep="\t", header=None)
NODES = 916428
EDGES = 5105039
#
NEW = csr_matrix((np.ones(len(data['i'])),(data['i'],data['j'])),shape=(NODES,NODES))
b = NEW.sum(axis=1)
NEW = NEW.transpose()
#
p0 = np.ones((NODES,1))/NODES
eps = 10**-5
delta = 0.15
ERROR = True
k = 0
#
while (ERROR == True):
with np.errstate(divide='ignore'):
z = p0 / b
p1 = (1-delta) * NEW.dot(csr_matrix(z)) + delta * np.ones((NODES,1))/NODES
if (ln.norm(p1-p0) < eps):
ERROR = False
k = k + 1
# PageRank
p0 = p1
Sur les graphiques, nous pouvons voir comment le vecteur p arrive à un état stationnaire v :

En utilisant le vecteur PageRank, vous pouvez également déterminer le vainqueur aux élections. Un petit sous-ensemble de contributeurs de Wikipédia sont des administrateurs, qui sont des utilisateurs ayant accès à des fonctionnalités techniques supplémentaires pour faciliter la maintenance. Pour qu'un utilisateur devienne administrateur, une demande d'administrateur est émise et la communauté Wikipédia, par le biais d'un commentaire public ou d'un vote, décide qui promouvoir au poste d'administrateur.
Le problème du PageRank peut également être réduit à un problème de minimisation et résolu en utilisant la méthode du gradient conditionnel de Frank-Wolfe, qui est la suivante: sélectionnez l'un des sommets du simplexe et faites un point de départ à ce sommet. Mise en œuvre de cette méthode sur les données - le lien est présenté ci-dessous:
#
data = pd.read_csv("grad.txt", names = ['i','j'], sep="\t", header=None)
NODES = 6301
EDGES = 20777
#
NEW = csr_matrix((np.ones(len(data['i'])),(data['i'],data['j'])),shape=(NODES,NODES))
b = NEW.sum(axis=1)
NEW = NEW.transpose()
e = np.ones(NODES)
with np.errstate(divide='ignore'):
z = e / b
NEW = NEW.dot(csr_matrix(z))
#
eps = 0.05
k=0
a_0 = 1
y = np.zeros((NODES,1))
p0 = np.ones((NODES,1))/NODES
#
p0[0] = 0.1
y[np.argmin(df(p0))] = 1
p1 = (1-2/(1+k))*p0 + 2/(1+k)*y
#
while ((ln.norm(p1-p0) > eps)):
y = np.zeros((NODES,1))
k = k + 1
p0 = p1
y[np.argmin(df(p0))] = 1
p1 = (1-2/(1+k))*p0 + 2/(1+k)*y

Pour le fonctionnement efficace d'un véritable moteur de recherche, la vitesse de calcul du vecteur PageRank est plus importante que la précision de son calcul. MPI ne vous permet pas de sacrifier la précision au profit de la vitesse de calcul. L'algorithme de Monte Carlo aide dans une certaine mesure à faire face à ce problème. Nous lançons un utilisateur virtuel qui déambule dans les pages des sites. En collectant des statistiques de leurs visites sur les pages du site, après une période assez longue, nous obtenons pour chaque page le nombre de fois que l'utilisateur l'a visitée. En normalisant ce vecteur, nous obtenons le vecteur PageRank souhaité. Laissez-nous vous montrer comment cet algorithme fonctionne sur des données déjà utilisées .
#
def get_edges(m, i):
if (i == NODES):
return random.randint(0, NODES)
else:
if (len(m.indices[m.indptr[i] : m.indptr[i+1]]) != 0):
return np.random.choice(m.indices[m.indptr[i] : m.indptr[i+1]])
else:
return NODES
#
data = pd.read_csv("web-Google.txt", names = ['i','j'], sep="\t", header=None)
NODES = 916428
EDGES = 5105039
NEW = csr_matrix((np.ones(len(data['i'])),(data['i'],data['j'])),shape=(NODES,NODES))
#c , total –
for total in range(1000000,2000000,100000):
#
k = random.randint(0, NODES)
# PageRank
ans = np.zeros(NODES+1)
margin2 = np.zeros(NODES)
ans_prev = np.zeros(NODES)
for t in range(total):
j = get_edges(NEW, k)
ans[j] = ans[j]+1
k = j
#
ans = np.delete(ans, len(ans)-1)
ans = ans/sum(ans)
for number in range(len(ans)):
margin2[number] = ans[number] - ans_prev[number]
ans_prev = ans
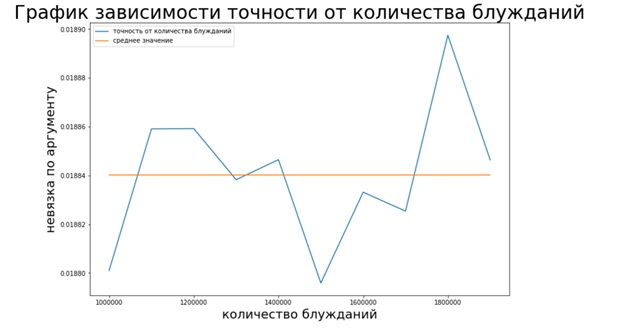
Comme le montre le graphique, la méthode de Monte Carlo, contrairement aux deux méthodes précédentes, n'est pas stable (il n'y a pas de convergence), cependant, elle aide à estimer le vecteur Page Rank sans nécessiter beaucoup de temps.
Conclusion: Ainsi, nous avons considéré les principaux algorithmes pour déterminer le PageRank des graphiques Web. Avant de commencer à concevoir un site Web, vous devez vous assurer que le PageRank n'est pas gaspillé en prêtant attention aux éléments suivants:
- Les liens internes montrent comment la «puissance des liens» s'accumule sur votre site, alors concentrez-vous sur les informations importantes sur la page d'accueil du site, car la page «d'accueil» du site a le PageRank le plus fort.
- Pages orphelines qui ne sont pas liées à d'autres pages de votre site. Essayez d'éviter de telles pages.
- Il convient de mentionner les liens externes s'ils sont utiles pour le visiteur de votre site.
- Les liens entrants cassés diluent le poids global de la page, vous devez donc les surveiller périodiquement et les «corriger» si nécessaire.
Cependant, cela ne signifie pas que vous devez vous concentrer sur le PageRank. Mais, il convient de rappeler qu'en prêtant attention à la structure du site lors de sa construction, aux fonctionnalités des liens internes et externes, vous optimisez le site pour le PageRank.