Algorithme de Kosaraju par étagère

En fait, il existe déjà un article sur Habré sur cet algorithme, mais il ne couvre pas la preuve de l'exactitude et certaines étapes de l'algorithme. J'ai décidé de créer une version plus de référence de cet article avec une analyse complète.

Cet article sera utile pour les étudiants qui étudient la discipline "Algorithmes et Théorie des Graphiques", ainsi que pour ceux qui souhaitent améliorer / rafraîchir leurs connaissances des algorithmes sur les graphiques.

Afin de comprendre l'algorithme de Kosarayu, vous devez connaître certains concepts de la théorie des graphes

Concepts de base

Les sommets u, v sont appelés fortement connectés si le graphe G contient un chemin (pas forcément une ligne droite) u → v Et v → u (On note les sommets fortement connectés par u↔v)

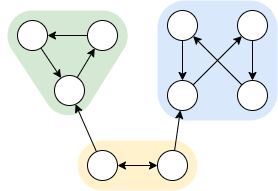
Les composants fortement connectés sont des sous-graphes fortement connectés maximum par inclusion.

Inverser le graphique - changer la direction de toutes les arêtes du graphique à l'opposé (une arête bidirectionnelle reste elle-même)

Inverser un graphique - le processus de rotation des bords dans la direction opposée (un bord bidirectionnel restera lui-même)

Plusieurs lemmes assez évidents peuvent être cités:

1. Un composant fortement connecté est l'ensemble des sommets inclus dans l'ensemble des cycles qui

ont au moins un sommet commun

2.

3. u ↔ v v ↔ w, u ↔ v ↔ w

4.

:

1. (DFS), «» . «», DFS  ( ).

   
   
   
   
   

   DFS  

   
   
   
   
   

2. 
   
   
   
   

3. DFS .

   
   
   
   
   

DFS

, : : , :

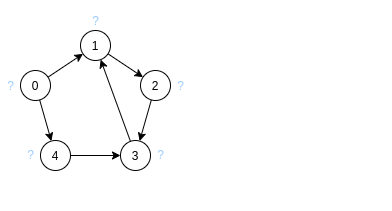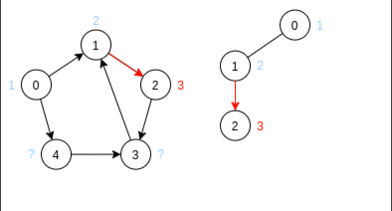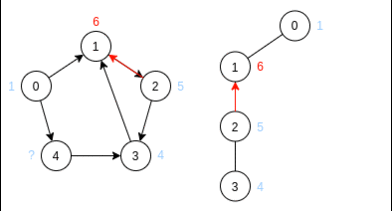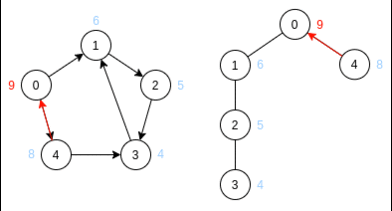
1. DFS

   
   
   
   
   

2. ( , , )

   
   
   
   
   

,

:

1:

'?'

DFS ( 2 , ; , , )



, - ( ) 1



, () ( ) -- DFS -- .

2:

3:

DFS, ,





DFS

3

, :

u v ⇔ DFS

:

⇒

u v G, ( 2), , .

⇐

u v . , r .

r 3 , 1 , u v. 2 :

1. r . u r v r ( 2). u v ( 3)

   
   
   
   
   

2. r , v. r v , r — ( , v , r, ). ( , ), , v r 3 ( )

   
   
   
   
   

, 1 2 , u v

O(V+E)

, , O(V+E) . ( )

, O(V+E)

, — O(V+E)

, O(V+E) .

, .

Par exemple: projeter un réseau de transport sur un graphe. L'algorithme aidera à vérifier le réseau de transport nouvellement créé pour l'accessibilité de chaque sommet à partir de chaque sommet (pour s'assurer qu'il y a un chemin de la périphérie au centre et à l'arrière).

Vous pouvez tester le système de conduits dans les bâtiments avec un algorithme; flux de courant dans les dispositifs à semi-conducteurs

Vous pouvez penser plus largement: nous projetons le système circulatoire d'un être vivant que vous avez été chargé de créer dans le cadre d'un projet de génie génétique, quelque part en 2077). L'algorithme vous aidera à savoir si le sang passe du cœur aux organes et retour.