Bonjour, chers Habradams et Habragospoda. Dans cet article, nous allons fermer au maximum les trappes de notre bathyscaphe, ajouter de la vitesse à notre moteur Python et plonger dans le gouffre des statistiques, à une profondeur où la lumière du soleil ne pénètre pratiquement pas. À cette profondeur, nous rencontrerons beaucoup de toutes sortes de tests statistiques qui flottent devant nous sous la forme de formules fantaisistes. Au début, il nous semblera qu'ils sont tous disposés différemment, mais nous essaierons d'aller au fond de la principale force motrice de toutes ces étranges créatures.
De quoi dois-je vous avertir avant de plonger à cette profondeur ? Tout d'abord, je suppose que vous avez déjà lu le livre "Statistiques pour tous" de Sarah Boslaf, et aussi fouillé dans la documentation officielle du module de statistiques de la bibliothèque SciPy. Excusez-moi pour ma prochaine supposition, mais il me semble que vous étiez probablement un peu abasourdi par le nombre de tests disponibles, et encore plus abasourdi lorsque vous avez réalisé que ce n'était vraiment que la pointe de l'iceberg. Eh bien, si vous n'avez pas encore rencontré tous les délices de cette merveilleuse "puberté", alors je vous recommande de vous procurer le livre d'Alexander Ivanovich Kobzar "Statistiques mathématiques appliquées. Pour les ingénieurs et les scientifiques". Eh bien, si vous êtes "dans le sujet", alors regardez toujours sous le chat,Pourquoi? Parce que la présentation et l'interprétation des faits sont parfois plus importantes et intéressantes que les faits eux-mêmes.
, :
import numpy as np
import pandas as pd
from scipy import stats
import matplotlib.pyplot as plt
import seaborn as sns
from pylab import rcParams
sns.set()
rcParams['figure.figsize'] = 10, 6
%config InlineBackend.figure_format = 'svg'
np.random.seed(42)
, , . , , - , , . [0; 10] 0 - "", 10 - " ". , :
![x_ {1} = [7.68, \; \; 5.40, \; \; 3,99, \; \; 3.27, \;\; 2,70, \; \; 5.85, \; \; 6.53, \;\; 5.00, \; \; 4.60, \; \; 6.18]](https://habrastorage.org/getpro/habr/upload_files/148/fc2/b25/148fc2b253952e2994d7a369321c13dd.svg)
- , - , - . :
![x_ {2} = [1.33, \; \; 1.66, \; \; 2,76, \; \; 4.56, \; \; 4,75, \; \; 0,70, \; \; 3.13, \;\; 1,96, \; \; 4.60, \; \; 3,69]](https://habrastorage.org/getpro/habr/upload_files/2ef/3a1/e2c/2ef3a1e2c921ee1c0773552e277b2276.svg)
, , , . , . , . , .. . " Pthon - " -.
, , . " , , ", - , , . , : , , .. .. , :
" " ;
" " ;
" " .
, . , , . :
x1 = np.array([7.68,5.40,3.99,3.27,2.70,5.85,6.53,5.00,4.60,6.18])
x2 = np.array([1.33,1.66,2.76,4.56,4.75,0.70,3.13,1.96,4.60,3.69])
fig, ax = plt.subplots()
sns.ecdfplot(x=x1, ax=ax, label=' ')
sns.ecdfplot(x=x2, ax=ax, label='')
ax.legend();
, , ( ), , :
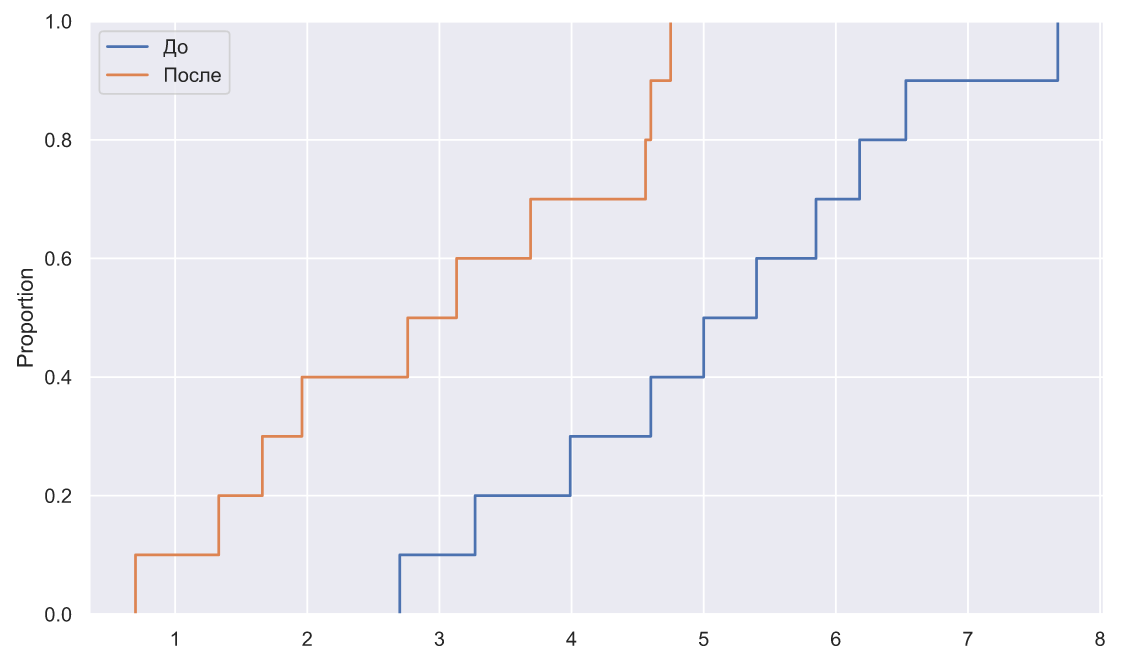
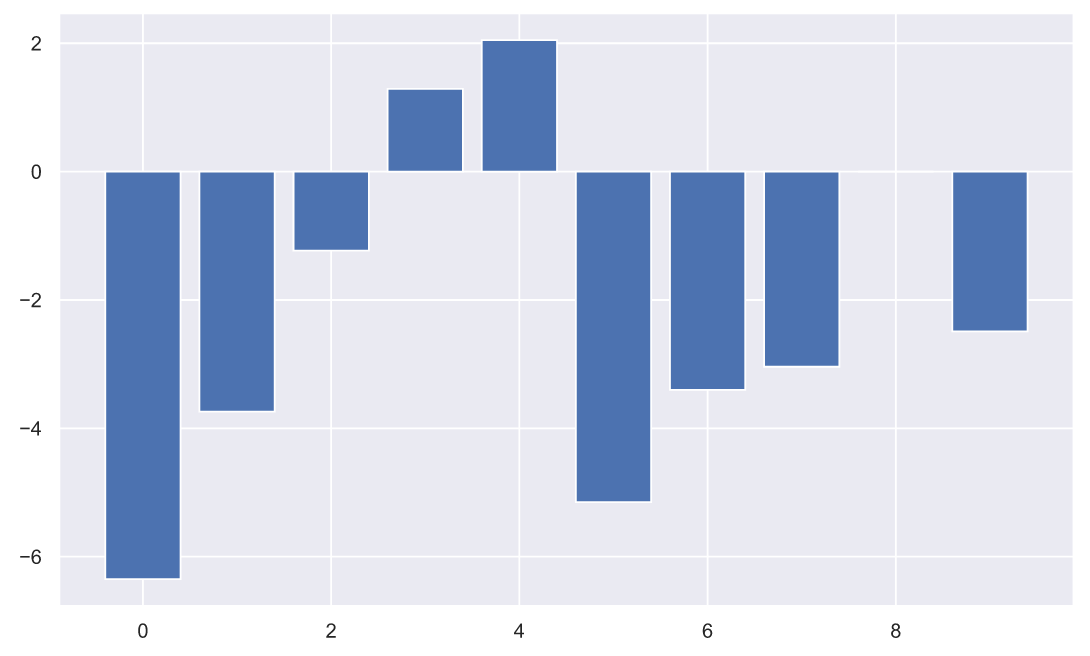
plt.bar(np.arange(10), (x2-x1));
, - . , , , . , :
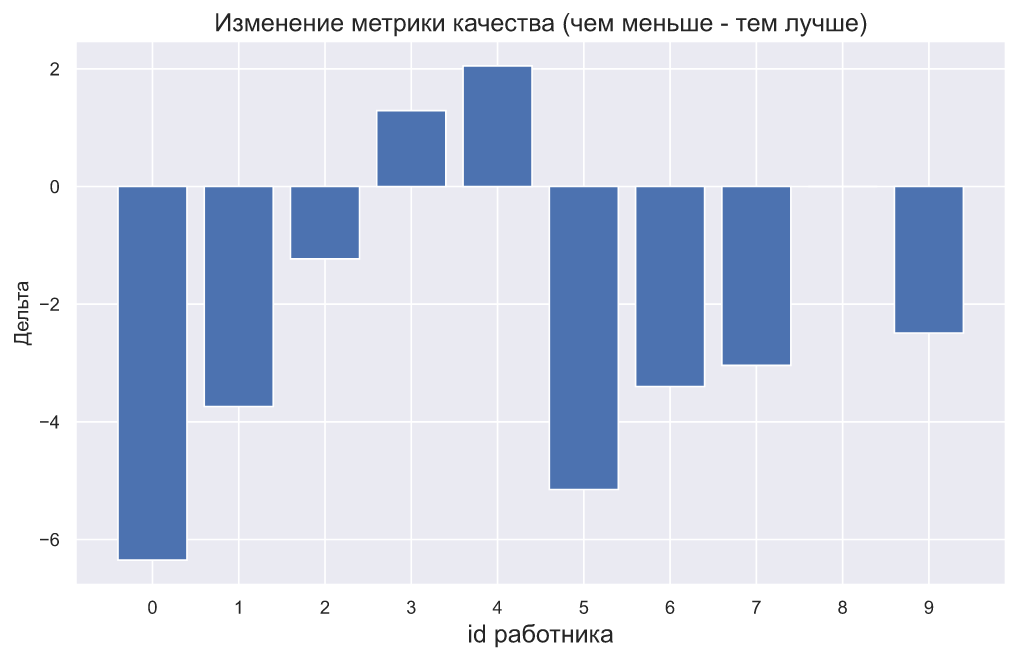
plt.bar(np.arange(10), (x2-x1))
plt.xticks(np.arange(10));
plt.title(' ( - )',
fontsize=15)
plt.xlabel('id ', fontsize=15)
plt.ylabel('');
:
plt.bar(np.arange(10) - 0.2, x1, width=0.4, label='')
plt.bar(np.arange(10) + 0.2, x2, width=0.4, label='')
plt.xticks(np.arange(10))
plt.legend()
plt.title(' ( - )',
fontsize=15)
plt.xlabel('id ', fontsize=15)
plt.ylabel('');
, - , , , . , . , , , , . - .
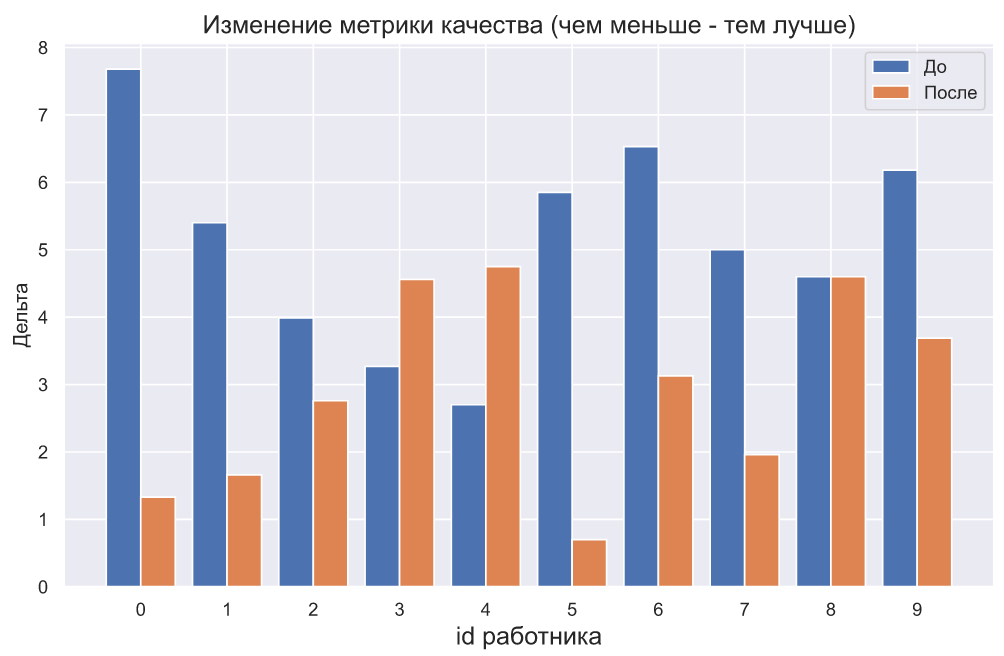
, - t- :
stats.ttest_rel(x2, x1)
Ttest_relResult(statistic=-2.5653968678354184, pvalue=0.03041662395965993)
c p-value 0.03 , . , . - . ?
:
print(f'mean(x1) = {x1.mean():.3}')
print(f'mean(x2) = {x2.mean():.3}')
print('-'*15)
print(f'std(x1) = {x1.std(ddof=1):.3}')
print(f'std(x2) = {x2.std(ddof=1):.3}')
mean(x1) = 5.12
mean(x2) = 2.91
---------------
std(x1) = 1.53
std(x2) = 1.47
t- , , (, ), . ? , ? ? , , .. , . , ?
( ) - -. , () , . , - . - , . , , - - . - , .
, t- , , . , . , . , ?
, . 5000 
10 , :
samples = stats.norm.rvs(loc=(5, 3), scale=1.5, size=(5000, 10, 2))
deviations = samples.var(axis=1, ddof=1)
deviations_df = pd.DataFrame(deviations, columns=['s1', 's2'])
sns.histplot(data=deviations_df, element="poly", color='r', fill=False);
, , "" - . :
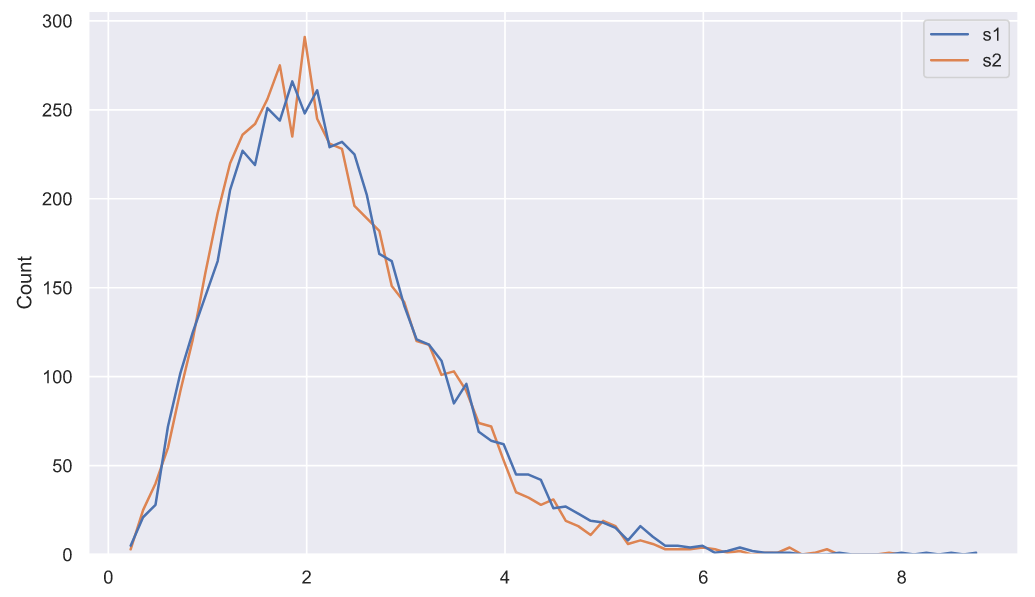
sns.histplot(data=pd.DataFrame(np.std(stats.norm.rvs(loc=(5, 3), scale=1.5, size=(5000,10,2)), axis=1, ddof=1), columns=['s1', 's2']), element="poly", color='r', fill=False);
"" - . - , , :
- ;
;
, .
, - "", "". " ", .. . , , , . , .
, . , , , . : "" . , ", " - , - . , fit():
df1, loc1, scale1 = stats.chi2.fit(deviations_df['s1'], fdf=10)
print(f'df1 = {df1}, loc1 = {loc1:<8.4}, scale1 = {scale1:.3}')
df2, loc2, scale2 = stats.chi2.fit(deviations_df['s2'], fdf=10)
print(f'df2 = {df2}, loc2 = {loc2:<8.4}, scale1 = {scale2:.3}')
df1 = 10, loc1 = -0.1027 , scale1 = 0.238
df2 = 10, loc2 = -0.08352, scale1 = 0.231
fig, ax = plt.subplots()
# ,
# 0.5 1:
sns.histplot(data=deviations_df['s1'], color='r', element='poly',
fill=False, stat='density', label='s1', ax=ax)
sns.histplot(data=deviations_df['s2'], color='b', element='poly',
fill=False, stat='density', label='s2', ax=ax)
chi2_rv1 = stats.chi2(df1, loc1, scale1)
chi2_rv2 = stats.chi2(df2, loc2, scale2)
x = np.linspace(0, 8, 300)
sns.lineplot(x=x, y=chi2_rv1.pdf(x), color='r', label='pdf(s1)', ax=ax)
sns.lineplot(x=x, y=chi2_rv2.pdf(x), color='b', label='pdf(s2)', ax=ax)
ax.set_xticks(np.arange(10))
ax.set_xlabel('s');
- . , , , , , , ( ). . , (""), ("") ("") (""), , , . , , , "" , , .
? , , 
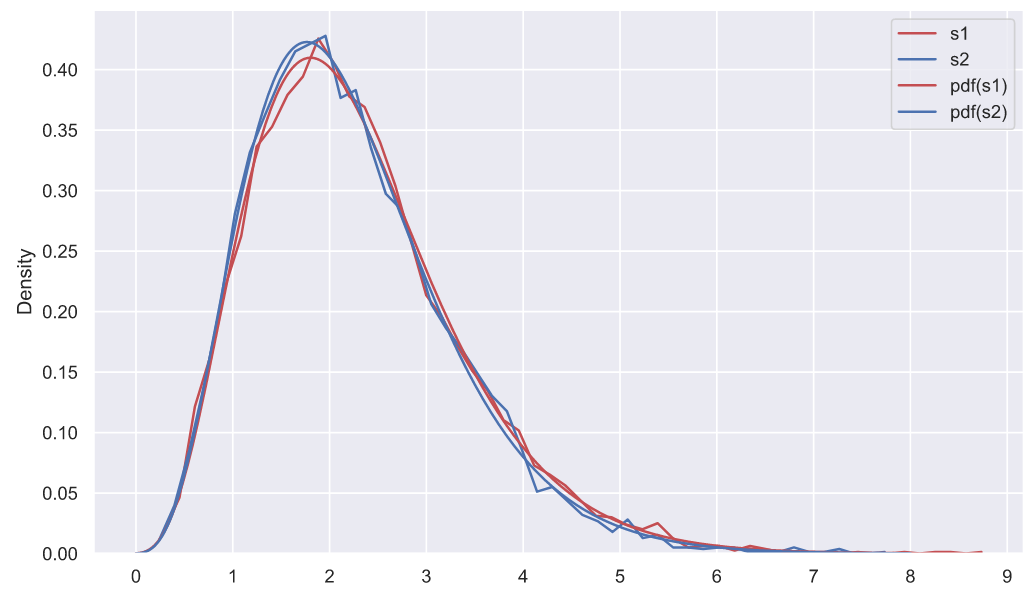
. , . ? , 2, 
?
fig, ax = plt.subplots()
var = 2**2
x = np.linspace(0, 10, 300)
sns.lineplot(x=x, y=chi2_rv1.pdf(x), label='pdf(s1)', ax=ax)
ax.vlines(var, 0, chi2_rv1.pdf(var), color='r', lw=2)
ax.fill_between(x[x>var], chi2_rv1.pdf(x[x>var]),
np.zeros(len(x[x>var])), alpha=0.3, color='b')
ax.hlines(0, x.min(), x.max(), lw=1, color='k')
p = chi2_rv1.sf(var)
ax.set_title(f'$P(s_{1} \geqslant {var}) = $' + '{:.3}'.format(p))
ax.set_xlabel('s');
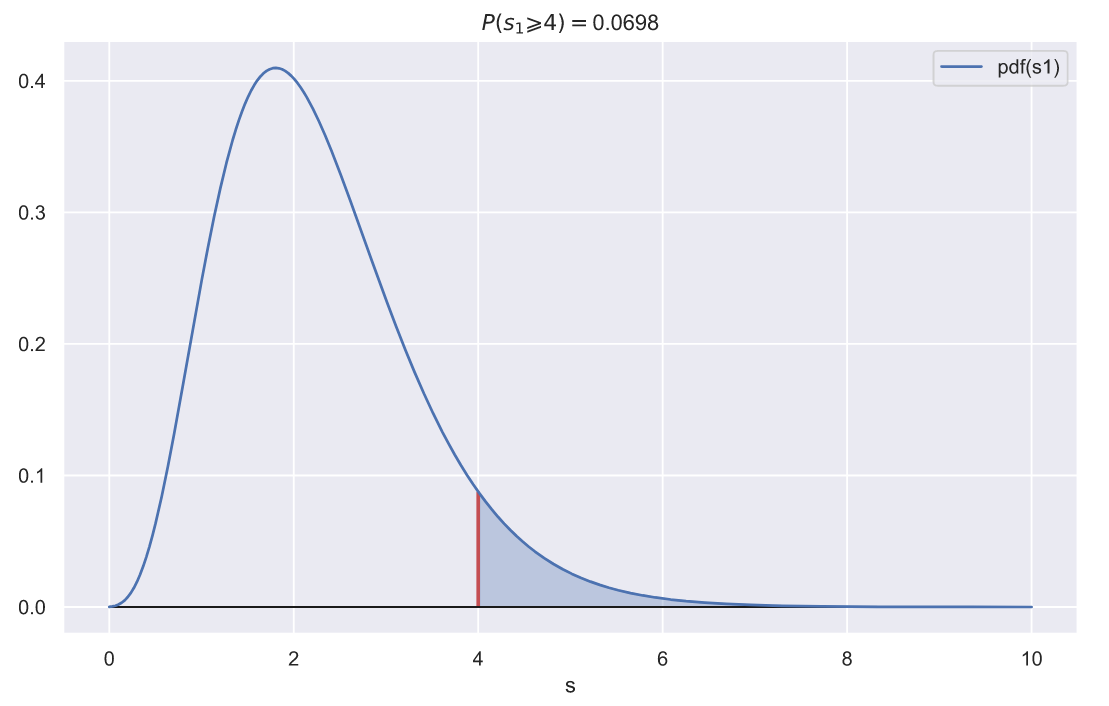
p-value , , , 10 
. , 
1.5. , 
, - , .
, - , , 0.1:
fig, ax = plt.subplots()
x = np.linspace(0, 10, 300)
sns.lineplot(x=x, y=chi2_rv1.pdf(x), label='pdf(s1)', ax=ax)
# :
ci_left, ci_right = chi2_rv1.interval(0.9)
ax.vlines([ci_left, ci_right], 0, 0.5, color='r', lw=2)
x_le_ci_l, x_ge_ci_r = x[x<ci_left], x[x>ci_right]
ax.fill_between(x_le_ci_l, chi2_rv1.pdf(x_le_ci_l),
np.zeros(len(x_le_ci_l)), alpha=0.3, color='b')
ax.fill_between(x_ge_ci_r, chi2_rv1.pdf(x_ge_ci_r),
np.zeros(len(x_ge_ci_r)), alpha=0.3, color='b')
ax.set_title(f'P({ci_left:.3} $\geqslant s_{1} \geqslant$ {ci_right:.3}) = 0.1')
ax.hlines(0, x.min(), x.max(), lw=1, color='k')
ax.set_xlabel('s');
, 
, - , , .
? , - . , :
:
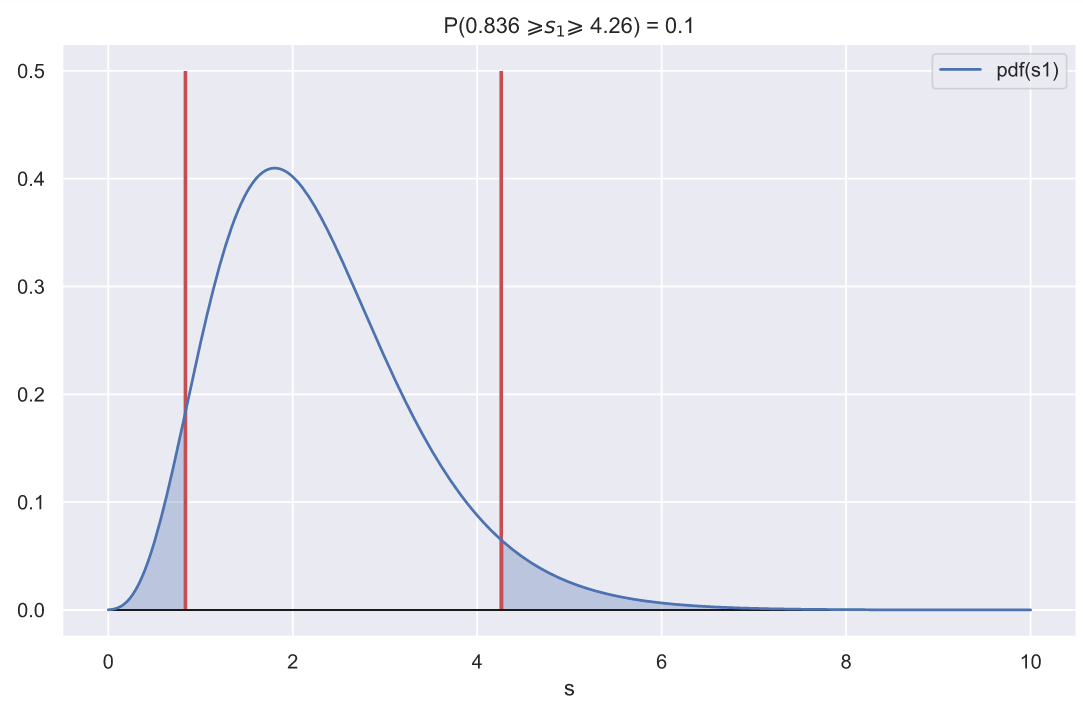
rel_dev = deviations_df['s1'] / deviations_df['s2']
sns.histplot(x=rel_dev, stat='density');
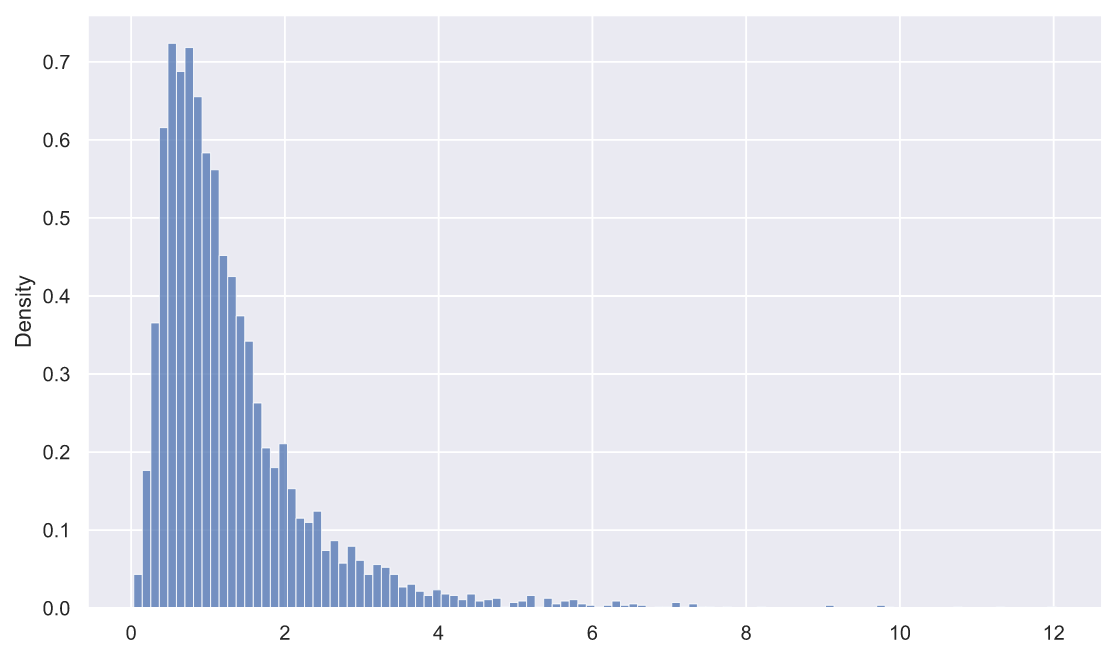
, fit():
dfn, dfd, loc, scale = stats.f.fit(rel_dev, fdfn=10, fdfd=10)
print(f'dfn = {dfn}, dfd = {dfd}, loc2 = {loc2:<8.4}, scale1 = {scale2:.3}')
dfn = 10, dfd = 10, loc2 = -0.08352, scale1 = 0.231
fig, ax = plt.subplots()
rel_dev = deviations_df['s1'] / deviations_df['s2']
sns.histplot(x=rel_dev, stat='density', alpha=0.4)
f_rv = stats.f(dfn, dfd, loc, scale)
x = np.linspace(0, 12, 300)
ax.plot(x, f_rv.pdf(x), color='r')
ax.set_xlim(0, 8);
. , 3, 1, :
fig, ax = plt.subplots()
rel_var = 3
x = np.linspace(0, 8, 300)
sns.lineplot(x=x, y=f_rv.pdf(x), label='pdf(s1)', ax=ax)
ax.vlines(rel_var, 0, f_rv.pdf(rel_var), color='r', lw=2)
ax.fill_between(x[x>rel_var], f_rv.pdf(x[x>rel_var]),
np.zeros(len(x[x>rel_var])), alpha=0.3, color='b')
ax.hlines(0, x.min(), x.max(), lw=1, color='k')
p = f_rv.sf(var)
ax.set_title(f'$P(s_{1}/s_{2} \geqslant {rel_var}) = $' + '{:.3}'.format(p))
ax.set_xlabel('s');
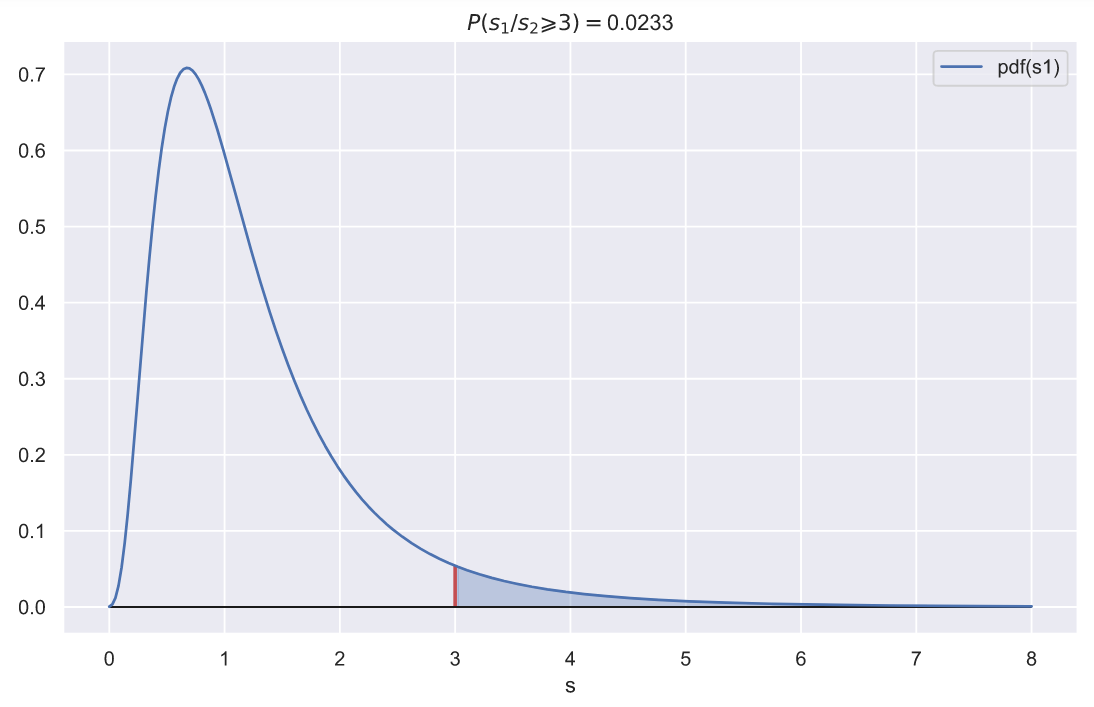
, 10 
, , 3, 0.023. , .
:
np.var(x1, ddof=1) / np.var(x2, ddof=1)
1.083553459313125
. , , . , ? ANOVA? , , , , . f_oneway() ( pvalue, , ):
stats.f_oneway(x1, x2)
F_onewayResult(statistic=10.786061383971454, pvalue=0.0041224402038065235)
? - ?
, f_oneway(), :
m1, m2, m = *np.mean((x1, x2), axis=1), np.mean((x1, x2))
ms_bg = (10*(m1 - m)**2 + 10*(m2 - m)**2)/(2 - 1)
ms_wg = (np.sum((x1 - m1)**2) + np.sum((x2 - m2)**2))/(20 - 2)
s = ms_bg/ms_wg
p = stats.f.sf(s, dfn=1, dfd=18)
print(f'statistic = {s:.5}, p-value = {p:.5}')
statistic = 10.786, p-value = 0.0041224
(mean square between group) , . , , 
. 
(mean square within group) , , . , , , . , - , , . , , 
:
:
N = 10000
samples_1 = stats.norm.rvs(loc=0, scale=1, size=(N, 10))
samples_2 = stats.norm.rvs(loc=0, scale=1, size=(N, 10))
m1 = samples_1.mean(axis=1)
m2 = samples_2.mean(axis=1)
m = np.hstack((samples_1, samples_2)).mean(axis=1)
ms_bg = 10*((m1 - m)**2 + (m2 - m)**2)
ss_1 = np.sum((samples_1 - m1.reshape(N, 1))**2, axis=1)
ss_2 = np.sum((samples_2 - m2.reshape(N, 1))**2, axis=1)
ms_wg = (ss_1 + ss_2)/18
statistics = ms_bg/ms_wg
f, ax = plt.subplots()
x = np.linspace(0.02, 30, 500)
plt.plot(x, stats.f.pdf(x, dfn=1, dfd=18), color='r', label=f'f.pdf(x, 1, 18, 0, 1)')
plt.legend()
sns.histplot(x=statistics, binwidth=0.1, stat='density', alpha=0.5)
ax.set_xlim(0, 6)
ax.set_title(r' $MS_{bg} \; / \;MS_{wg}$ ');
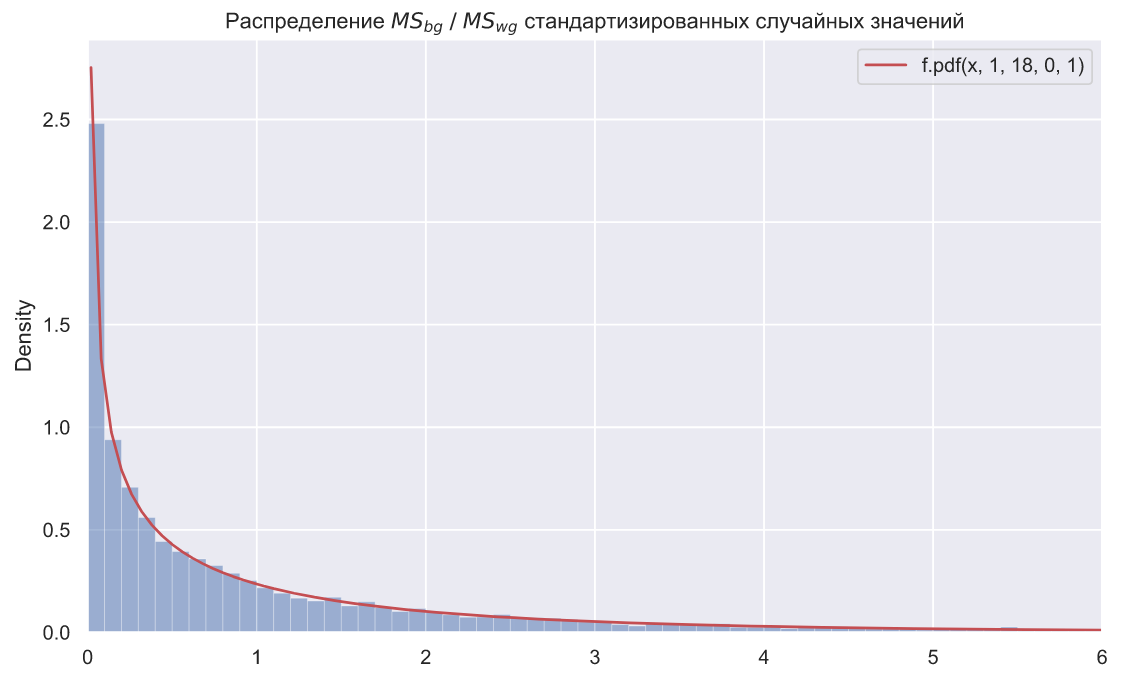
N = 10000
mu_1 = stats.uniform.rvs(loc=0, scale=5, size=(N, 1))
samples_1 = stats.norm.rvs(loc=mu_1, scale=2, size=(N, 10))
mu_2 = stats.uniform.rvs(loc=0, scale=5, size=(N, 1))
samples_2 = stats.norm.rvs(loc=mu_2, scale=2, size=(N, 10))
m1 = samples_1.mean(axis=1)
m2 = samples_2.mean(axis=1)
m = np.hstack((samples_1, samples_2)).mean(axis=1)
ms_bg = 10*((m1 - m)**2 + (m2 - m)**2)
ss_1 = np.sum((samples_1 - m1.reshape(N, 1))**2, axis=1)
ss_2 = np.sum((samples_2 - m2.reshape(N, 1))**2, axis=1)
ms_wg = (ss_1 + ss_2)/18
statistics = ms_bg/ms_wg
loc, scale = stats.f.fit(statistics, fdfn=1, fdfd=18)[-2:]
f, ax = plt.subplots()
x = np.linspace(0.02, 30, 500)
plt.plot(x, stats.f.pdf(x, dfn=1, dfd=18, loc=loc, scale=scale), color='r', label=f'f.pdf(x, 1, 18, {loc:.3}, {scale:.3})')
plt.legend()
sns.histplot(x=statistics, binwidth=0.2, stat='density', alpha=0.5)
ax.set_xlim(0, 20)
ax.set_title(r' $MS_{bg} \; / \;MS_{wg}$ ');
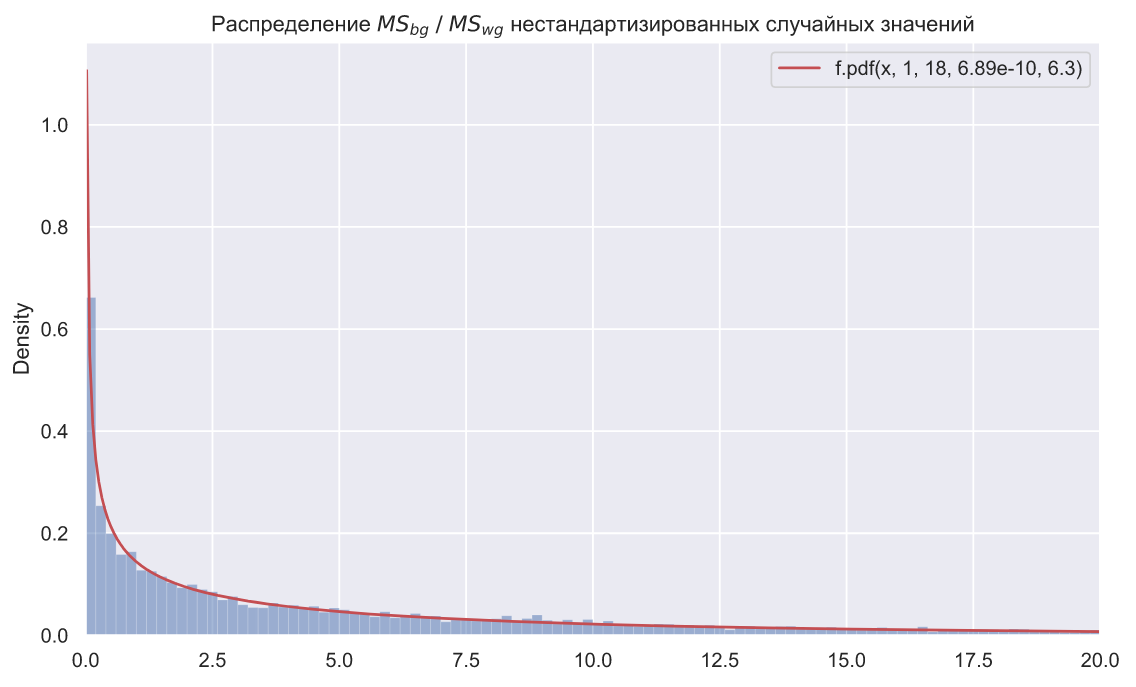
, SciPy levene(). () , ANOVA, :
stats.levene(x1, x2)
LeveneResult(statistic=0.0047521397921121405, pvalue=0.9458007897725039)
""
, , . , , , , , . , , . : 10000 5 , , , :
N, k = 10000, 5
func = [stats.uniform, stats.norm, stats.laplace]
color = list('gyb')
labels = ['s_uniform', 's_norm', 's_laplace']
for i in range(3):
ss = np.square(func[i].rvs(size=(N, k))).sum(axis=1)
sns.histplot(x=ss, stat='density', label=labels[i] + '.pdf(x)',
element='step', color=color[i], lw=2, fill=False)
x = np.linspace(0, 25, 300)
plt.plot(x, stats.chi2.pdf(x, df=5), color='r', label='chi2.pdf(x, df=5)')
plt.legend()
plt.xlim(0, 20);
, - , , , "" . , , , - (- - ).
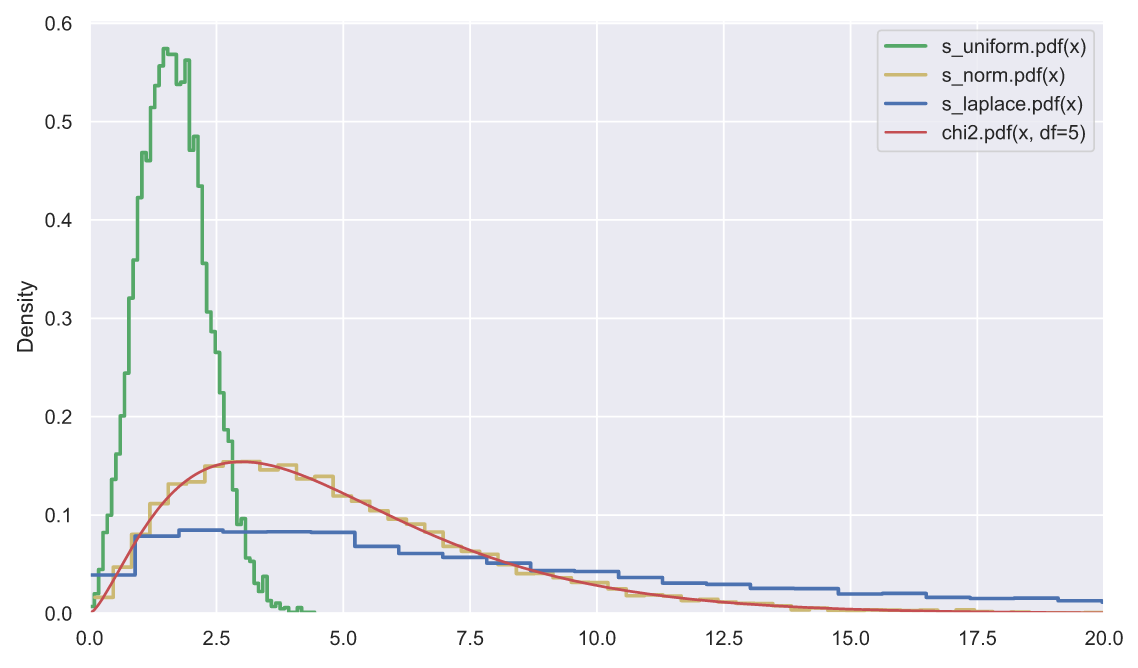
- ANOVA, , "" ? , :
array([0.40572556, 0.67443266, 0.38765587, 0.96540199, 0.57933085])
, - . ? 50 5 , , , :
s = np.sort(stats.norm.rvs(size=(50000, 5)), axis=1).T
for i in range(5):
sns.histplot(x=s[i], stat='density',
label='i = ' + str(i),
element='poly', lw=2, fill=False)
plt.xticks(np.arange(-5, 6))
plt.legend();
, ? , , , . , :
" " ;
;
( );
- , ( );
.
, , , , "" . ?!! , , - :
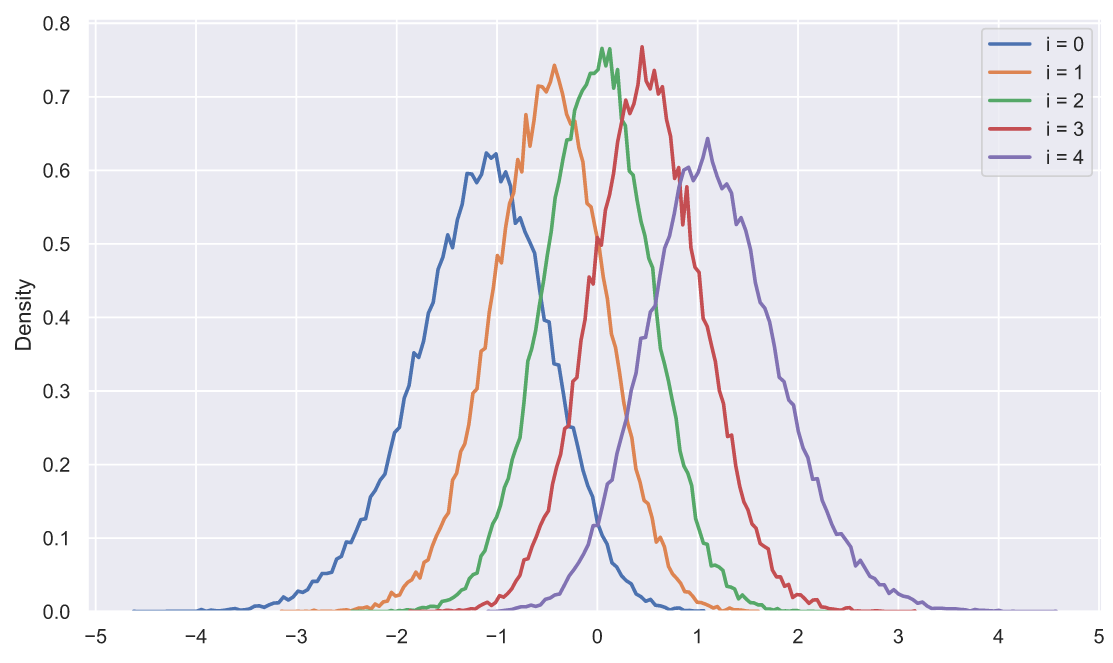
s = np.sort(stats.norm.rvs(size=(50000, 5)), axis=1).T
sample = np.sort(stats.norm.rvs(size=5))
colors = sns.color_palette('tab10', 5)
for i in range(5):
sns.histplot(x=s[i], stat='density',
label='i = ' + str(i),
element='poly', lw=2, fill=False,
color=sns.color_palette('pastel', 5)[i])
plt.vlines(sample[i], 0, 0.8, lw=2, zorder=10,
color=sns.color_palette('tab10', 5)[i])
plt.xticks(np.arange(-5, 6))
plt.legend();
- :
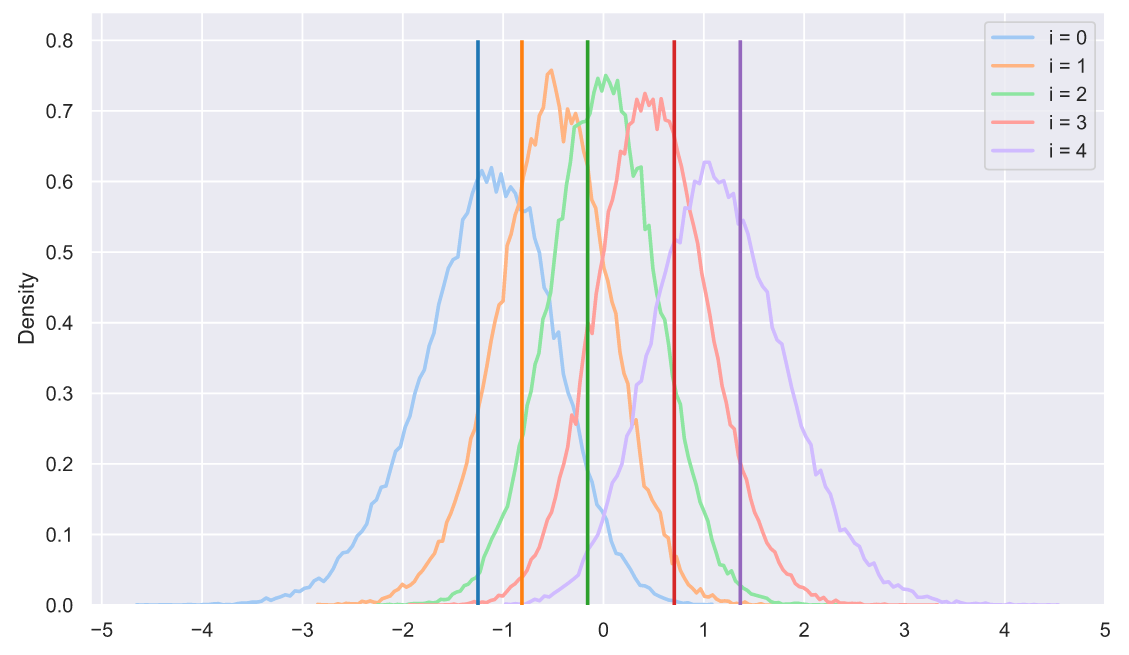
s = np.sort(stats.norm.rvs(size=(50000, 5)), axis=1).T
sample = np.sort(stats.uniform.rvs(loc=-2, scale=4, size=5))
colors = sns.color_palette('tab10', 5)
for i in range(5):
sns.histplot(x=s[i], stat='density',
label='i = ' + str(i),
element='poly', lw=2, fill=False,
color=sns.color_palette('pastel', 5)[i])
plt.vlines(sample[i], 0, 0.8, lw=2, zorder=10,
color=sns.color_palette('tab10', 5)[i])
plt.xticks(np.arange(-5, 6))
plt.legend();
, - . , , - . : , . , . , . :
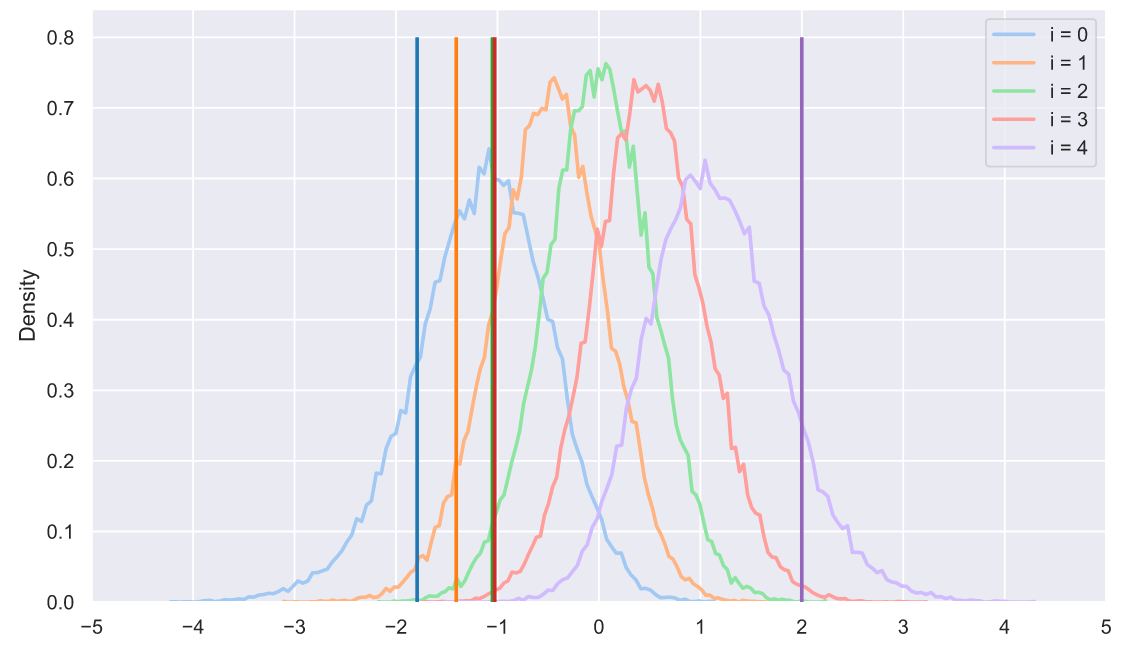
stats.ks_1samp(x1, stats.norm.cdf, args=(5, 1.5))
KstestResult(statistic=0.11452966409855592, pvalue=0.9971279018404035)
, p-value, , "" . , , . , , :
x1.sort()
n = len(x1)
ecdf_ge = np.r_[1:n+1]/n
ecdf_le = np.r_[0:n]/n
cdf_teor = stats.norm.cdf(x1, loc=5, scale=1.5)
plt.plot(x1, ecdf_ge, color='b', drawstyle='steps-post', label='ecdf_ge')
plt.plot(x1, cdf_teor, color='r', drawstyle='steps-post', label='cdf_teor')
plt.plot(x1, ecdf_le, color='g', drawstyle='steps-post', label='ecdf_le')
plt.legend();
, .. :
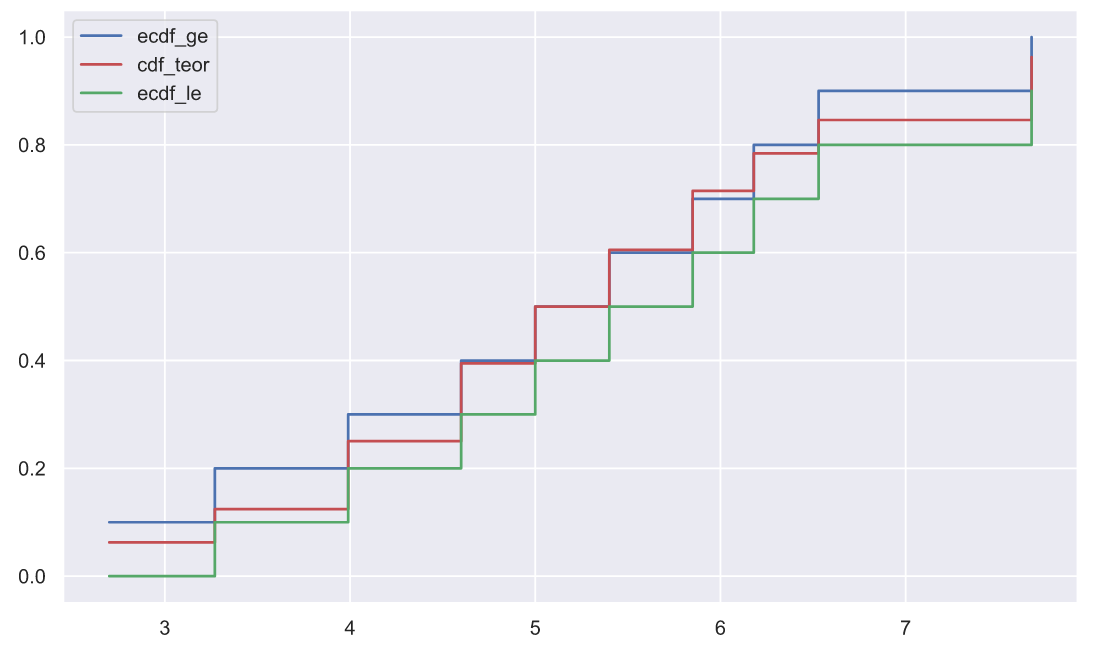
d_plus = ecdf_ge - cdf_teor d_minus = cdf_teor - ecdf_le statistic = np.max([d_plus, d_minus]) statistic
0.11452966409855592
( n=5):
x = np.linspace(0, 1, 3000)
plt.plot(x, stats.kstwo.pdf(x, n));
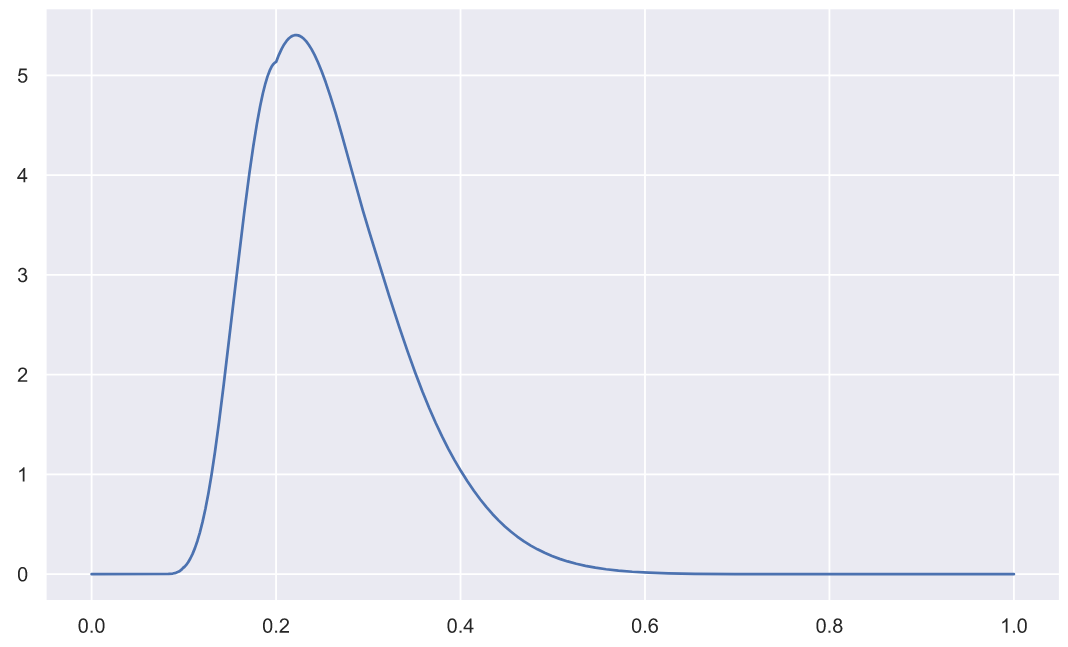
p-value:
pvalue = stats.kstwo.sf(statistic, n) pvalue
0.9971279018404035
, . , , ecdf_le ( ). , ecdf_le . , "" , seaborn, , .
, , -, , : " ?" , : " , ?" , . , - , , ? , . , - ? , .
Les articles scientifiques et techniques ne sont pas faciles à lire, mais les rédiger est encore plus fastidieux. J'aimerais transmettre des idées complexes de manière simple et détendue. J'aimerais espérer pouvoir le faire au moins un peu.
Quoi qu'il en soit, nous continuerons à plonger ! Dans la chanson d'Eminem "Mon nom est", j'ai une ligne préférée "Je viens de boire un cinquième de vodka - ose-moi conduire? (Allez-y)", qui convient très bien à toute la plongée.
Comme d'habitude, j'appuie sur F5 et j'attends vos commentaires avec impatience !