La relation entre la topographie et la gravité rappelle le problème bien connu de la poule et de l'œuf. D'une part, le relief affecte sans aucun doute la force de gravité mesurée à sa surface - le niveau du relief détermine la distance au centre de masse de la planète, et les élévations du relief contiennent des masses attractives supplémentaires. D'autre part, la force de gravité affecte aussi sans aucun doute le relief, ce qui est particulièrement visible dans les océans, dont la forme de la surface répète les anomalies de la force de gravité. De plus, la surface du relief est affectée par l'érosion éolienne et hydrique et de nombreux autres facteurs, de sorte que la nature de la relation entre le relief et la gravité devient difficile à prévoir. Les images spatiales reproduisent également les reliefs - ainsi que les formes et les couleurs de la végétation et tout le reste sur ce relief, de sorte que la nature de la relation entre les images et le relief est encore moins évidente.
Heureusement, le champ de gravité et le relief de surface de notre planète ont la propriété de fractalité, c'est-à-dire d'auto-similitude à différentes échelles, qui est la clé pour déterminer la nature de la relation entre eux.
Mesure de la dimension fractale
Il existe de nombreuses façons de définir la dimension fractale, et elles n'ont en commun que la présence d'une échelle spatiale caractéristique. Vous pouvez calculer la fractalité dans le domaine spatial, ou vous pouvez également dans le domaine fréquentiel (composantes du spectre spatial), différencier et intégrer... Le secret est que toute la variété des méthodes donne des résultats similaires et le choix d'une méthode particulière est assez arbitraire, il est seulement important de comprendre comment les résultats de la méthode de calcul choisie se comparent aux résultats d'autres méthodes (Gneiting et al., 2012).
, , , — .
( ) , ( ) . , ( ) , , — . , , . , , , , . , . , — . , , , . , N- N+1 . , () . , (), ( , , ). ́ ́ ́ ́ . . ́ ( , ) — , (, . . , 2008).
() , . , , . () (, , 1973). () , . , 80 !
. . , , . , ( ), , ( ) (. ). , . — (, ) , . — 10 ? , . 1 1000 ( 10 … 10 ), 4 ~6000 (2πR, R ), . . — 1 , , . : ( ), . , , 5-10 (, Sentinel-1 Sentinel-2). , . , , , , , «» , .
, . , ( ) . ( - — ) . , — , . , ( , ) .
, , :
́ ( … . στάσις – ), . , ( 100–150 ) . . [ — ]
, , , (. ):
… , . . . . [ — ]
, , . 1749. 1736, , , . [ — ]
()
:
. . 1914–15 . . - 1931 . . , , , . [ — ]
, ( ), . , , (), (100%).
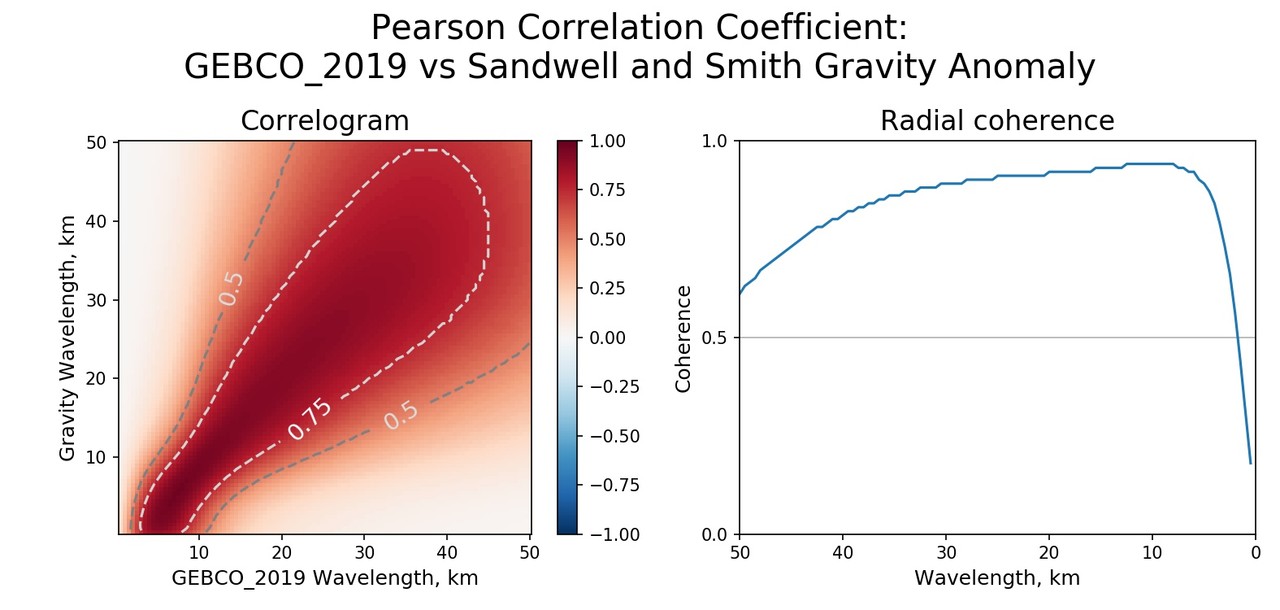
. (2.5 — 5 ). (90% ) ~15 , (75% ) ~35 , . , , , . 11 CRUST 1.0: A New Global Crustal Model at 1x1 Degrees, 15 , . 25 ( 35 ). , (), .
, :
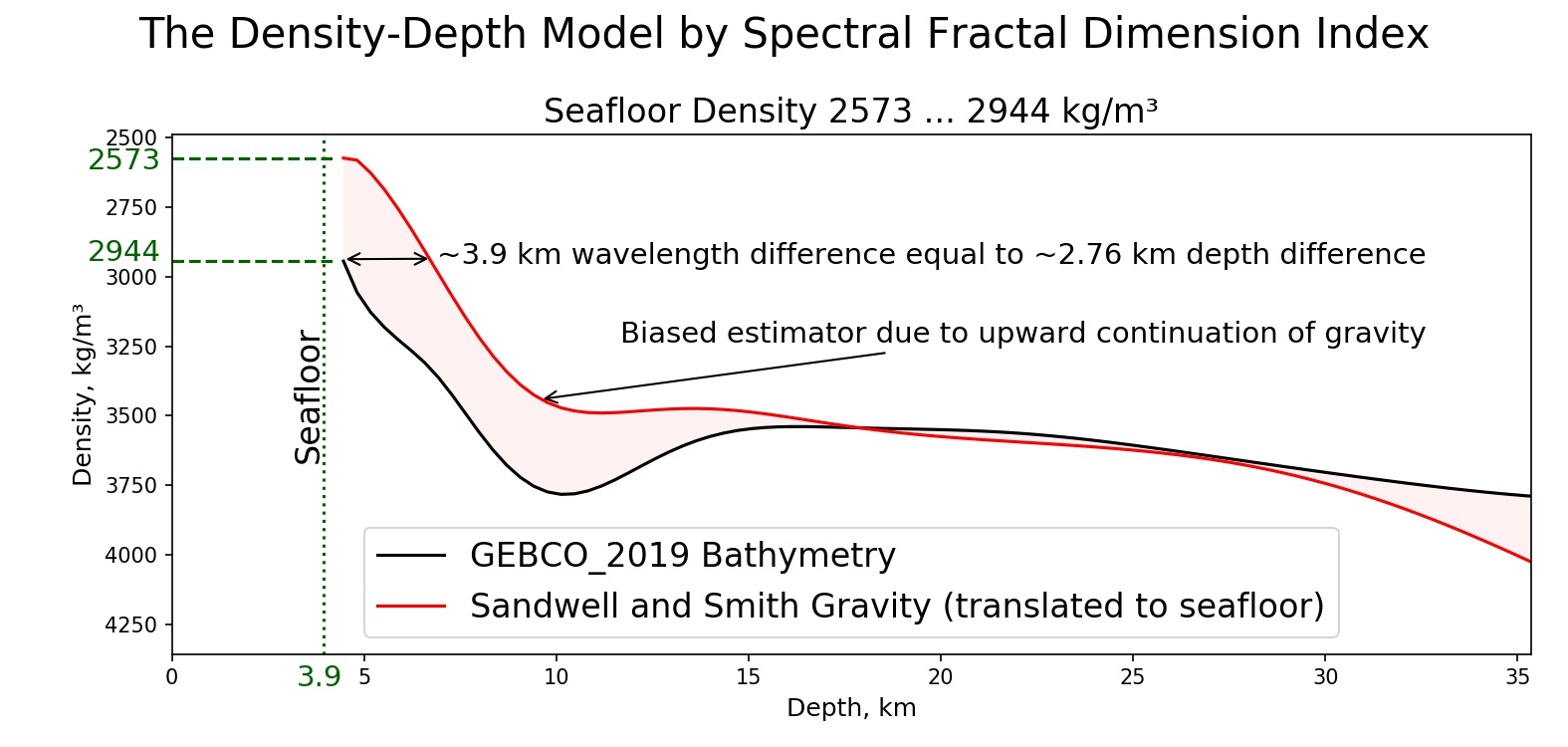
, , , . 15 35 , . , .
, , , (, ) , . , , , (). , , , . , , — , , - . , . - , . , , , .
, . , :
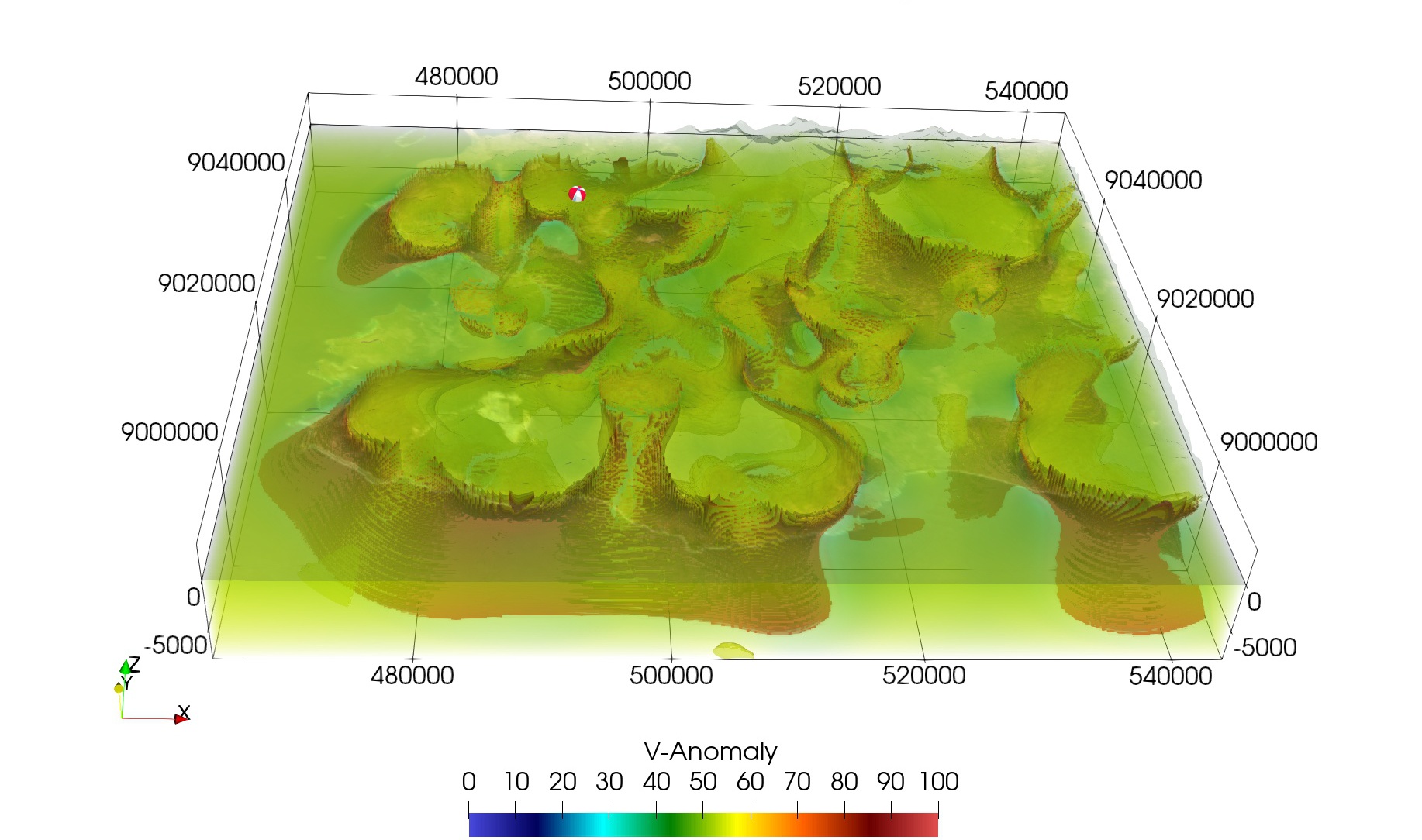
, , — . - , , , .
, , . , :

— , . , , .
, , — , .
()
, , () . , 20 , , . « », — , , , (Miranda et al., 2015). (Zhang, Featherstone, 2019) , , , .
, «» (, )? — . , , . , - , , — , , ( , , ).
,
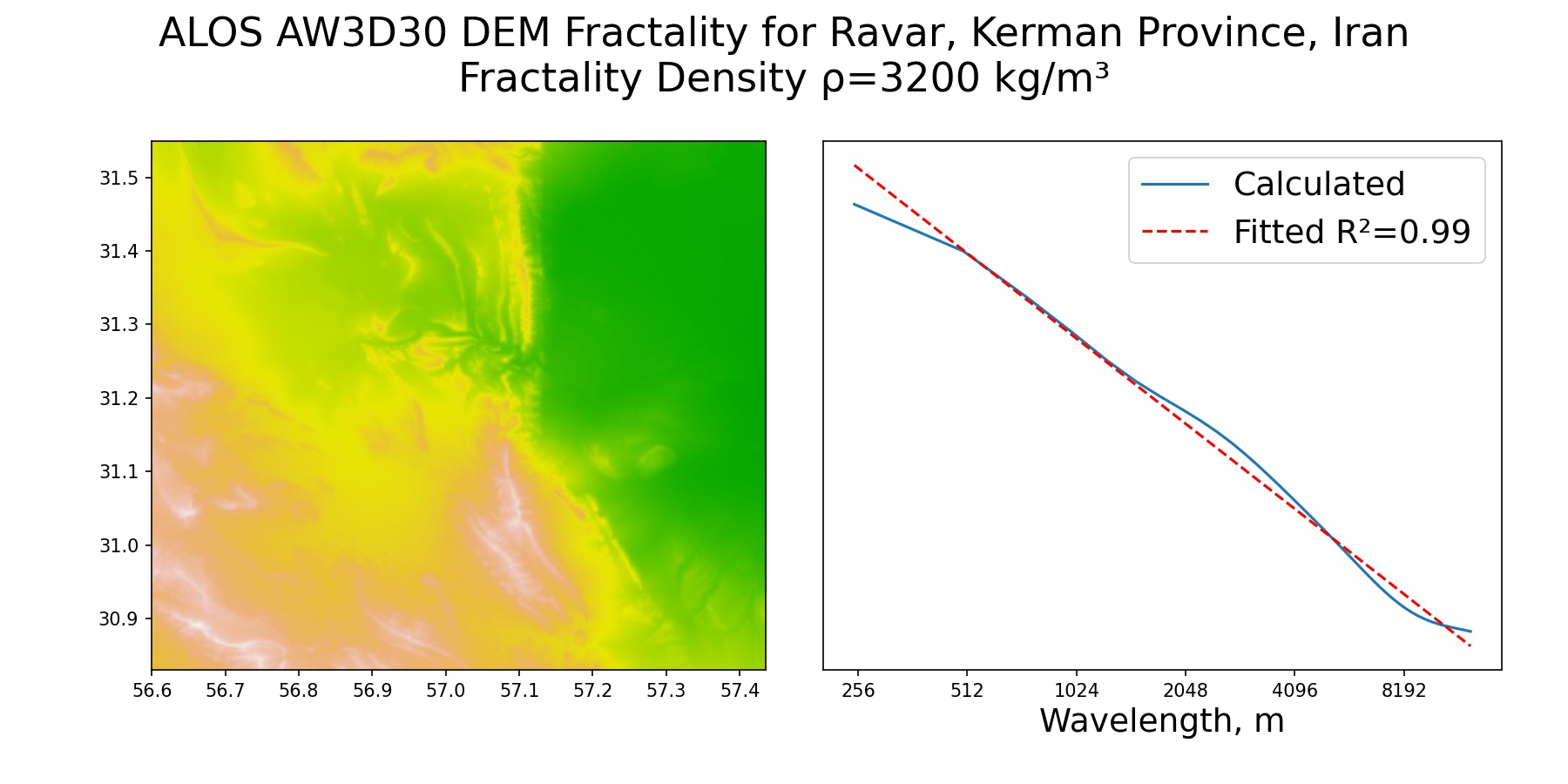
3D Density Inversion by Circular Hough Transform (Focal Average) and Fractality Index , , . , , , , , . , . , , . GitHub Geological Fractality on ALOS DEM AW3D30 and Sentinel-2 SUrface Reflectance Image for Ravar, Kerman Province, Iran:
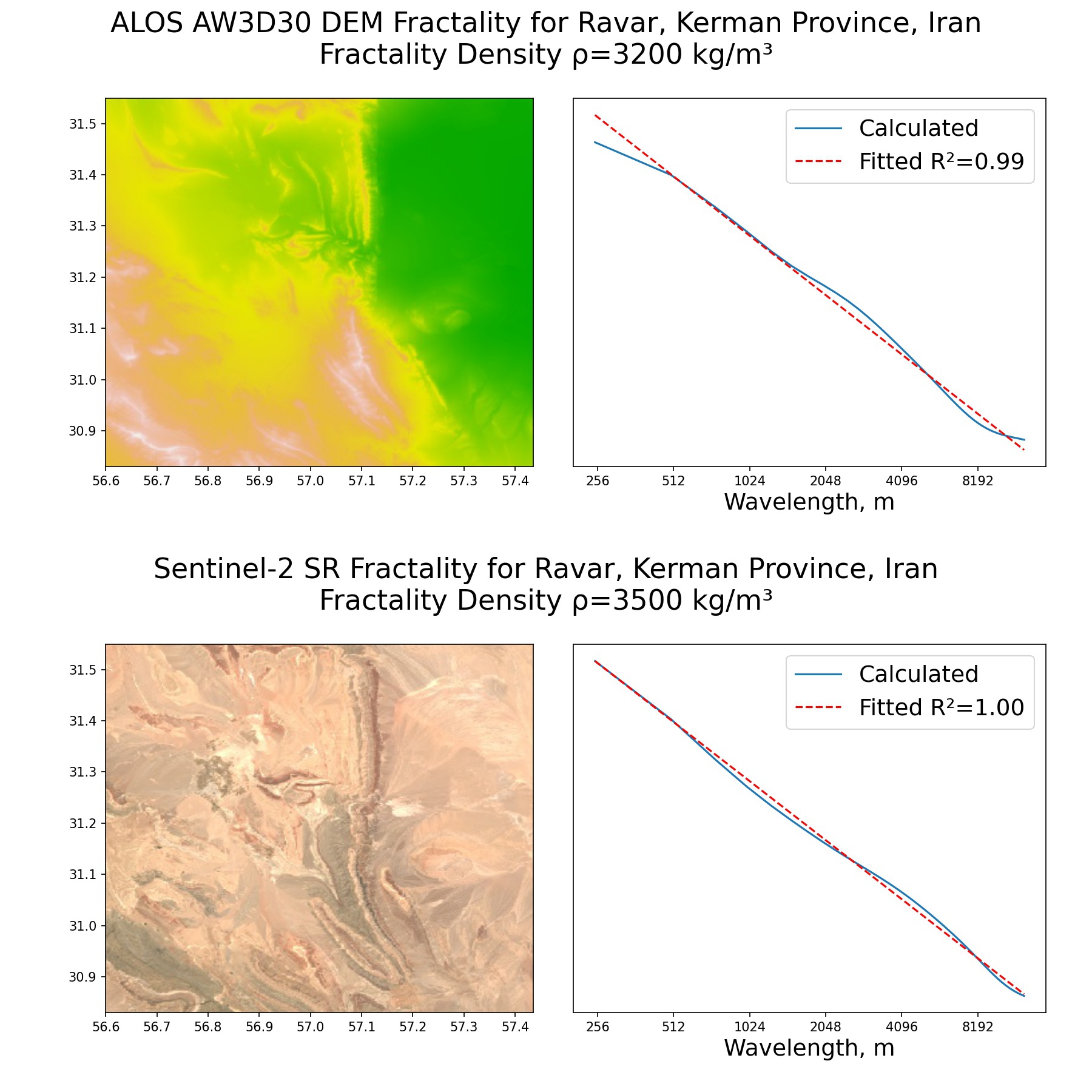
, , ρ=3200 kg/m³ R²=0.99, , . ρ=3500 kg/m³ R²=1.00, , . , , . , . . , , .
(), ! , — , , . , — , . , , , , .
, . . , . . , 1973. http://m.mathnet.ru/links/cd623304046883b7c36697e2e9f9b1d0/dan39067.pdf
, ..,1978. https://ikfia.ysn.ru/wp-content/uploads/2018/01/Malahov1978ru.pdf
, . . , . . , 2008. http://www.mathnet.ru/links/2a351947644994381a8272c4fc3ba0dd/jetpl108.pdf
Numerical simulation of the realizations and spectra of a quasi-multifractal diffusion process, A. I. Saichev & V. A. Filimonov, https://link.springer.com/article/10.1134/S0021364008090129
Gneiting, T., Ševčíková, H. & Percival, D. B. Estimators of Fractal Dimension: Assessing the Roughness of Time Series and Spatial Data. Statist. Sci. 27, 247–277 (2012).
Zhang, K. & Featherstone, W. Exploring the Detailed Structure of the Local Earth’s Gravity Field Using Fractal and Fourier Power Spectrum Techniques. (2019).
Miranda, S. A. et al. Fractalness of land gravity data and residual isostatic anomalies map of Argentina, Chile and western Uruguay. Geofísica internacional 54, 315–322 (2015).