
Né pour ramper ne peut pas voler. Cette phrase peut être utilisée à la fois dans un sens métaphorique et dans un sens littéral, car les créatures sans ailes (ou des parties du corps fonctionnellement similaires) ne sont vraiment pas capables de conquérir les cieux. Au moins la plupart d'entre eux. Une règle ne serait pas une règle s'il n'y avait pas d'exceptions. Dans l'aspect des vols sans ailes, il existe également des exceptions - des serpents arboricoles décorés ( Chrysopelea) Les représentants de ce genre de serpents sont capables de planer - une compétence extrêmement utile étant donné qu'ils vivent dans les cimes des arbres au-dessus du sol. Des scientifiques de la Virginia Polytechnic University (USA) ont décidé d'envisager le vol d'un cerf-volant sous l'angle de la cinématique. Quelles sont les caractéristiques anatomiques qui permettent aux serpents de voler (tomber de manière contrôlée, pour être exact), que se passe-t-il pendant le vol en termes de cinématique, et comment cette recherche peut-elle aider en robotique? Les réponses à ces questions nous attendent dans le rapport des scientifiques. Aller.
Base d'étude
Les serpents décorés sont un genre de serpents serpentins trouvés en Asie du Sud et du Sud-Est. Les représentants de ce genre ne peuvent pas se vanter de grandes dimensions (longueur du corps seulement de 0,6 à 1,5 m) et d'un poison mortel. Bien que la proie qu'ils chassent pendant la journée ne soit pas d'accord avec ce dernier. Compte tenu de l'habitat (couronnes des arbres), ces serpents ont très peu d'ennemis, ils n'ont donc pas de besoin particulier de poison fort. De plus, ils ont des tactiques beaucoup plus efficaces - ils savent planifier.

Les serpents volants, comme on les appelle communément, rampent à travers les arbres en utilisant des écailles dures le long de leur ventre, leur permettant de se déplacer verticalement. Si le serpent veut passer d'un arbre à un autre, il se glisse d'abord au bord de la branche, puis plie le corps sous la forme de la lettre latine "J" pour viser (pour déterminer l'angle souhaité de "décollage" et le site d'atterrissage). En disant «allons-y», le serpent pousse son corps vers l'avant et vers le haut, tirant dans son ventre et faisant saillie ses côtes (son corps devient donc plus plat et légèrement concave). Pendant le vol plané, le serpent fait constamment des mouvements de corps serpentins d'un côté à l'autre, ce qui lui permet de contrôler le vol et d'atterrir en douceur.
Vue latérale d'une longue planification d'un serpent volant Chrysopelea paradisi.
Un avantage supplémentaire de la méthode de mouvement si inhabituelle pour les serpents est les économies d'énergie impressionnantes, car le vol est beaucoup plus rapide (et plus sûr) que la rampe lente d'arbre en arbre au sol. De cette brève description seule, il est clair qu'il existe de nombreux éléments importants dans la mécanique du vol du serpent; angle de décollage, forme du corps pendant le décollage et le vol, mouvements du corps en vol, etc.
L'aspect le plus frappant, surtout pour les observateurs, du vol de l'aile est le mouvement ondulé du corps. Cette technique est utilisée par de nombreuses créatures de la planète pour se déplacer sur terre et sur l'eau. Vous n'avez pas besoin d'aller loin, car les serpents eux-mêmes l'utilisent parfaitement. Les scientifiques notent que le mouvement ondulant sur terre et sur eau a été assez bien étudié, mais de telles pirouettes dans l'air sont encore un mystère.
Chez les serpents Chrysopelea , l' ondulation est caractérisée par une forme de corps en forme de S, une faible fréquence d'ondulation (1–2 Hz) et une section transversale aérodynamique aplatie du corps.
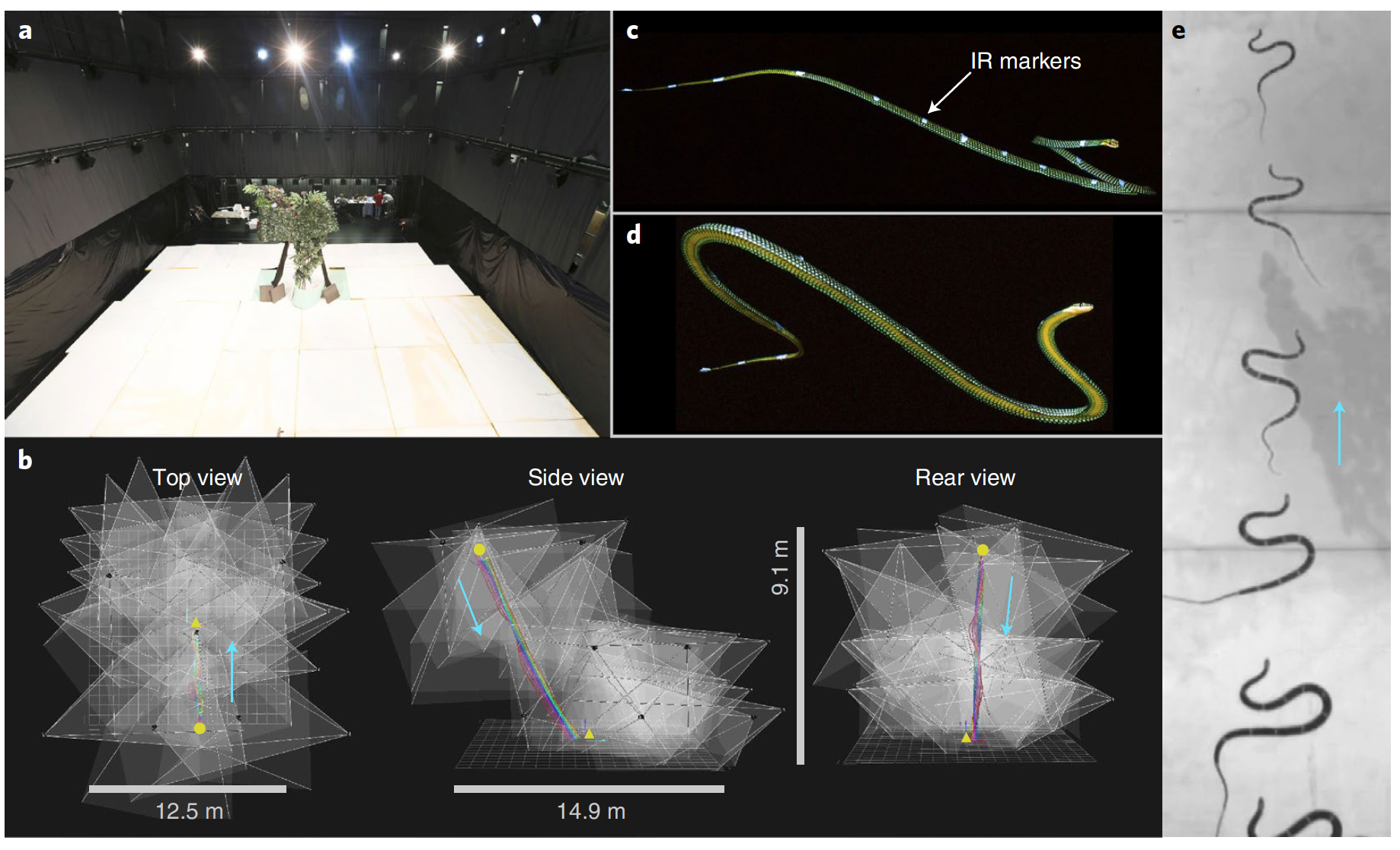
Image n ° 1
En fait, l'ondulation aérienne reconstruit continuellement le corps du serpent, le transformant en forme d'aile ( 1). Des recherches antérieures ont montré que les cerfs-volants volants effectuent toujours des mouvements ondulés en vol. Cependant, on ne sait pas si l'ondulation est une partie essentielle d'un vol réussi ou s'il s'agit simplement d'une habitude. l'aspect comportemental du mouvement à terre, a migré vers la fuite sans aucune intention.
Si nous prenons en compte l'ondulation sur terre et sur l'eau, nous pouvons supposer qu'elle génère une poussée dans l'air. Sur les milieux solides, un mouvement ondulant se produit en raison des forces de contact réparties sur les régions ventrale et latérale du corps, et dans l'eau, le déplacement ou l'absorption de fluide le long du corps provoque un mouvement vers l'avant. Dans les deux cas, la force motrice nette agit principalement dans le plan d'ondulation. La modulation du corps hors plan (vertical) peut être utilisée à des fins secondaires telles que la diminution de la résistance ou l'augmentation de la force normale.
Mais pour les cerfs-volants volants, une planification réussie nécessite la génération de forces aérodynamiques nécessaires pour compenser le poids de l'animal. Les forces de levage et de résistance sont créées par l'air circulant à travers le corps aplati lorsqu'il accélère vers le bas sous l'action de la gravité, tandis que le mouvement alternatif provoqué par les contractions musculaires n'augmente probablement pas la génération de force.
Vue de face du décollage et de l'aplatissement du serpent volant Chrysopelea paradisi.
Les forces aérodynamiques qui en résultent doivent agir en dehors du plan d'ondulation, et l'ondulation elle-même doit constamment modifier la répartition des forces sur le corps du serpent. Il convient également de considérer que les cerfs-volants volants peuvent «s'inquiéter» non seulement horizontalement, mais verticalement. Cela signifie que le modèle de vol de cerf-volant contient à la fois des éléments de tangage * et de roulis * .
Pas * - mouvement angulaire par rapport à l'axe d'inertie transversal horizontal.Dans cette étude, les scientifiques ont décidé d'examiner en détail le rôle de l'ondulation dans le vol du serpent. À l'aide d'enregistrements de vol de serpents à grande vitesse, les scientifiques ont pu quantifier l'ondulation aéroportée. Les données obtenues ont permis de créer un modèle tridimensionnel précis du vol de l'aile.
Rouleau * - mouvement angulaire par rapport à son axe longitudinal.
Résultats de recherche
L'ondulation aérienne consiste en un tas de vagues de flexion horizontale et verticale. 11 à 17 marqueurs ont été placés le long du corps des serpents (7 individus) participant au tir du vol (aire de décollage haute de 8,3 m). L'évaluation des changements de position de ces marqueurs vous permet de déterminer avec précision la structure de l'ondulation pendant le vol.
Vue de dessus sur la planification des tests d'un serpent volant Chrysopelea paradisi.
Marqueurs infrarouges obtenus en faisant planer un serpent volant, Chrysopelea paradisi.
Après 36 observations pratiques, les scientifiques ont créé un modèle 3D du corps du serpent ( r ).
Développement d'un modèle 3D d'un serpent volant Chrysopelea paradisi basé sur des données de capture de mouvement.
En utilisant le vecteur tangent (t̂ = ∂r / ∂s), il a été possible de décomposer l'ondulation en deux ondes de flexion angulaires qui se déplacent le long du corps.
Les ondes horizontales et verticales sont définies par les formules suivantes:
θ̅ (s, t) = -tan -1 t̂ x / t̂ y
et
ψ̅ (s, t) = sin -1 t̂ z
où θ̅ (s, t) et ψ̅ (s, t ) Sont les angles locaux que le corps forme par rapport aux directions horizontale et verticale, en fonction de la longueur d'arc s et du temps t.
Les données montrent que les cerfs-volants volants utilisent deux ondes: une onde horizontale avec une grande amplitude et une onde verticale avec une amplitude plus faible, qui descendent toutes les deux dans le corps de la tête à la queue (image n ° 2).

Image # 2
Ces ondes se forment après un transitoire initial lorsque le serpent saute dans une posture relativement droite et forme ensuite une posture en forme de S caractéristique pour le glissement.
Il y a quatre caractéristiques de l'ondulation de l'air qui associent une onde verticale à une onde horizontale ( 2a ). Premièrement, l'onde verticale a des fréquences spatiales et temporelles deux fois supérieures à celles de l'onde horizontale. Cela indique que le corps a deux fois plus de virages verticaux que de virages latéraux ( 2a ,2f ). Deuxièmement, les coudes en U sur le corps d'un cerf-volant volant peuvent être identifiés comme des passages à zéro sur le tracé de l'angle de pliage ( 2b ). Troisièmement, ces intersections sont les maxima de l'onde verticale, indiquant que les ondes horizontales et verticales sont déphasées de 90 °. Quatrièmement, la flexion maximale hors plan se produit aux coudes en U et approximativement au milieu des segments droits. Aux virages en U, la section transversale de «l'aile» du serpent est repliée en raison du mouvement du corps à l'extérieur du plan ( 1c , 1d ).
La forme des ondes progressives change avec le temps, à mesure que le serpent accélère et produit des forces aérodynamiques, cependant, certaines caractéristiques restent courantes. L'onde horizontale est une sinusoïde à sommet plat dont l'amplitude (80-120 °) dépend du nombre de périodes spatiales, avec moins de périodes conduisant à des angles de flexion horizontaux plus élevés. L'onde verticale est une sinusoïde à pic étroit avec de larges creux avec des amplitudes allant de 20 ° à 45 °.
Une évaluation quantitative des caractéristiques spatiales et temporelles des vagues a montré que les serpents utilisent des ondes horizontales avec 1–1,5 périodes spatiales et une fréquence d'onde de 1–1,7 Hz et des ondes verticales avec 2–3 périodes spatiales et une fréquence d'onde de 2–3,4 Hz.
Il y a un composant supplémentaire dans l'ondulation de l'air, que les scientifiques ont appelé «courbure dorsoventrale», représentant le mouvement de haut en bas de l'arrière du corps par rapport à la tête. L'angle d'inclinaison de ce virage variait de -20 ° à 30 °. Le coude dorsoventral était toujours présent dans les vols observés, mais n'avait pas de relation significative avec le nombre de périodes spatiales.
Pour déterminer avec précision le degré d'influence de la relation entre les ondes horizontales et verticales, ainsi que l'influence de la flexion dorsoventrale sur la dynamique du vol, les scientifiques ont créé un modèle anatomiquement précis d'un serpent en vol. La maîtrise du modèle permet, selon les scientifiques, de vérifier systématiquement comment les composantes de l'ondulation (l'amplitude de l'onde horizontale, le nombre de périodes spatiales et la fréquence d'ondulation) affectent la dynamique de planification à court et à long terme.
L'onde horizontale est modélisée comme une sinusoïde avec un pic plat de grande amplitude, et l'onde verticale est modélisée comme une sinusoïde de petite amplitude:
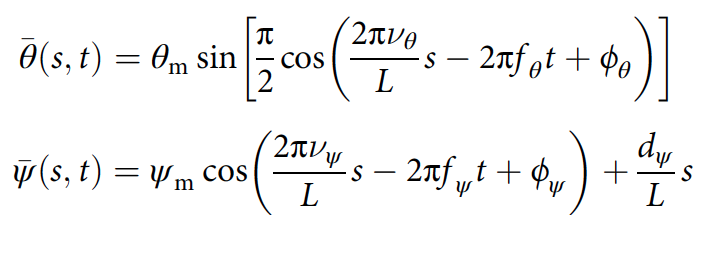
où θ m et ψ m sont les angles de flexion horizontaux et verticaux maximaux; ν est le nombre de périodes spatiales; f est la fréquence de l'ondulation; ϕ - déphasage; d ψ est l'angle de flexion dorsoventrale; L - longueur du corps ( 2f , 2g ).
Les ondes horizontales et verticales sont connectées dans les données cinématiques ( 2e ): ν ψ = 2ν θ , f ψ = 2f θ et ϕ ψ = 2 (ϕ θ- π / 2). Cela simplifie grandement le modèle à 5 variables qui déterminent la forme du corps: θ m , ψ m , ν θ , f θ et d ψ .
La position r = [x, y, z] du corps par rapport au centre de masse est calculée comme suit: ∂ s x = cosψ̅sinθ̅, ∂ s y = -cosψ̅cosθ̅ et ∂ s z = sinψ̅.
La position du centre de masse R 0 et l'orientation du corps (angles de lacet * , tangage et roulis) sont déterminées en intégrant les équations du mouvement de translation et de rotation.
Lacet * - mouvement angulaire par rapport à l'axe vertical.
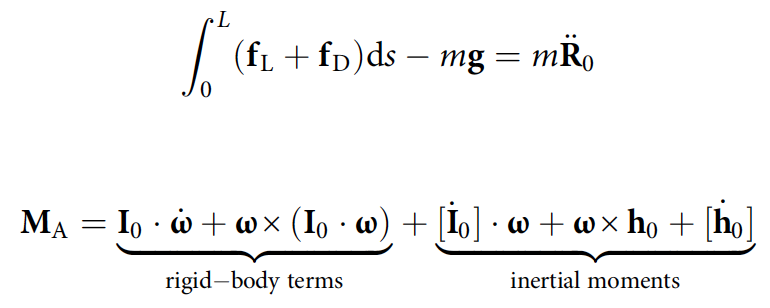
où f L et f D sont des forces de levage et de résistance infinitésimales; M A - moment aérodynamique; m est la masse du serpent.
Pour confirmer que le modèle mathématique produit des résultats physiquement réalistes, les scientifiques ont simulé des vols en utilisant des paramètres obtenus à partir d'observations de vol à voile réelles de cerfs-volants réels (la comparaison des simulations et des observations est montrée dans l'image ci-dessous).

Image n ° 3
À en juger par comparaison, le modèle fonctionne, mais il comporte quelques inexactitudes mineures qui doivent être corrigées à l'avenir.
Pour vérifier l'influence de l'ondulation sur les caractéristiques de planification, deux simulations ont été réalisées: avec f θ = 0 Hz (sans ondulation) et f θ= 1,2 Hz (fréquence moyenne d'ondulation chez les serpents). Dans les deux cas, ν θ et θ m ont varié ( 4a ).

Image №4 Les
données cinématiques de la forme du corps de serpent dans le modèle ont permis d'obtenir 121 formes avec 1 ≤ ν θ ≤ 1,5 ondes corporelles et des amplitudes d'ondes horizontales dans la plage de 90 ° ≤ θ m ≤ 119 °. De plus, les formes corporelles observées ont été extraites de ce tableau (partie médiane du graphique, séparée le long de la diagonale; 4b ). La partie du graphique qui est mise en évidence ci-dessous contient les formes de corps «ouvertes» (ressemblant à la lettre S) et la partie supérieure - «fermée» (ressemblant à un signe de l'infini).
L'amplitude de l'onde verticale et l'angle dorsoventral ont été maintenus à un niveau constant: 20 ° et 10 °, respectivement. La simulation était considérée comme terminée lorsque le centre de masse du serpent touchait le sol (atterrissage) ou lorsque l'un des angles d'orientation dépassait le seuil de 85 °. Si cela se produisait, alors la planification était considérée comme instable, c.-à-d. pas le même que dans la nature. Pendant la simulation, la dynamique à court terme (hauteur de départ 10 m) et la dynamique à long terme (hauteur de départ 75 m) avec / sans ondulation ont été testées.
Le modèle montre que les ondulations ont un effet positif sur les performances de glisse, augmentant généralement les distances horizontales et verticales parcourues avant que le cerf-volant simulé ne devienne instable.
Simulation d'un serpent volant glissant avec et sans ondulation.
Les glissements courts avec une hauteur de lancement de 10 m ont montré un bon coefficient de stabilité en présence d'ondulation (94%). Si l'ondulation n'était pas incluse dans le modèle, alors seulement 50% des vols étaient stables. L'ondulation augmente également la distance de planification (de 4 m à 4,3 m).
Lors de la simulation de plané à partir de 75 m, l'ondulation a augmenté la distance horizontale et verticale avant que l'instabilité ne se manifeste dans 86% des lancements. Dans ce cas, l'ondulation a également augmenté la distance de vol dans 92% des lancements. L'ondulation a également augmenté la distance horizontale moyenne de 6,9 m.
Pour clarifier l'influence de l'amplitude de l'onde verticale et de la flexion dorsoventrale sur la dynamique de glissement, différentes valeurs de ces paramètres ont été utilisées dans la modélisation et les résultats ont été considérés.
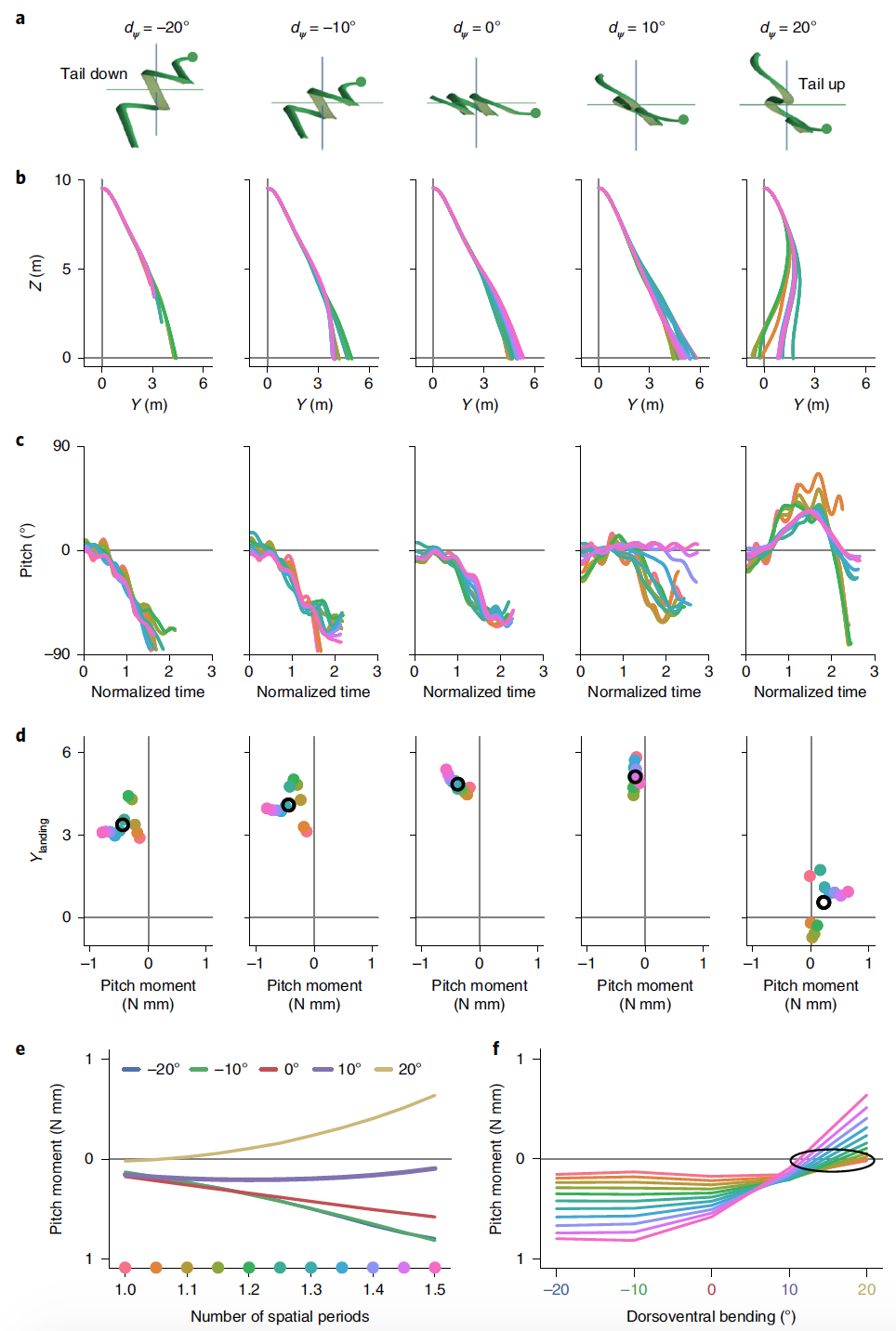
Image n ° 5 La
planification a été simulée avec ψ m = 0 °, 10 ° et 20 ° et une courbure dorsoventrale de -20 ° à 20 ° par pas de 10 ° ( 5a ) pour 11 formes de corps différentes.
Les vibrations verticales ont un effet relativement faible sur la trajectoire de planification, tandis que la flexion dorsoventrale a un effet significatif.
Un serpent parfaitement plat (ψ m= 0 °), qui n'a jamais été observé lors des tests expérimentaux, a montré les pires résultats attendus. L'augmentation de l'amplitude de l'onde verticale a augmenté l'efficacité de la planification en raison de la torsion de la section transversale dans le plan, qui fournit un angle plus favorable pour créer la force ( 2j ).
Contrairement à l'amplitude de l'onde verticale, le virage dorsoventral avait un effet notable sur les caractéristiques de planification, en particulier sur le terrain.
À ψ m = −20 ° avec le dos du corps sous la tête, le glissement n'était pas superficiel, au contraire il est devenu instable en hauteur jusqu'à tomber de 10 m. À ψ m= 20 ° avec l'arrière du corps au-dessus de la tête, la trajectoire est incurvée vers l'arrière, certaines morphologies atterrissant derrière le saut. Une telle mauvaise planification est justifiée par une inclinaison vers le haut du corps. Néanmoins, les planeurs avec les paramètres ci-dessus avaient une bonne stabilité en rotation.
Des simulations non tournantes ont été effectuées pour tester la relation entre les performances de flexion, de roulis et de glissement du corps dorsoventral. Au lieu de résoudre un système couplé non linéaire d'équations # 4 et # 5, les scientifiques ont échantillonné les forces aérodynamiques à différentes phases du corps pendant le cycle d'ondulation. Ensuite, l'équation n ° 4 a été intégrée ici, et la position et la vitesse du centre de masse ont été calculées.
Essentiellement, cette manipulation est une expérience de "soufflerie virtuelle" dans laquelle un modèle dynamique est utilisé pour calculer les forces distribuées agissant sur un corps lors de son accélération. Cette méthode vous permet d'éliminer la relation entre le mouvement de translation et de rotation afin de quantifier les contributions aérodynamiques et inertielles individuelles au mouvement de rotation.
Avec une augmentation du virage dorsoventral de -20 ° à 10 °, la position d'atterrissage du serpent simulé augmente à mesure que le tangage moyen augmente dans la direction zéro ( 5d ). À un virage dorsoventral de 20 °, le moment de tangage moyenné en phase devient positif et les performances de glissement diminuent.
Pour chaque angle du coude dorsoventral, l'efficacité de planification et le moment incliné moyen dépendent également de la forme utilisée, notamment du nombre de périodes spatiales et de l'amplitude de l'onde horizontale. Quelle que soit la forme du corps au moment de la planification, le virage dorsoventral a une grande influence sur le moment moyen du tangage, et à mesure que le nombre de périodes spatiales augmente, les moments divergent, devenant plus positifs ou négatifs en fonction de d ψ .
Les marques des moments de tangage moyennés en phase à 5e correspondent à la pente ascendante ou pente montrée en 5c et aux performances de glissement résultantes en 5b . À 5fon montre que pour les morphologies avec la plus petite période spatiale, le moment de tangage moyen sera le plus petit.
D'après les données décrites ci-dessus, on peut supposer que l'onde verticale fait rouler le corps hors du plan, modifiant l'orientation locale de «l'aile aplatie» (la forme du corps du serpent pendant le vol plané) à l'aide d'un flux d'air. La courbure dorsoventrale contrôle l'amplitude et le signe de l'élan aérodynamique qui affecte le corps. Un cerf-volant volant peut contrôler le moment de tangage en modifiant l'angle de courbure dorsoventrale ou la forme d'onde horizontale pendant le vol.
Par conséquent, la flexion dorsoventrale du corps joue un rôle extrêmement important dans la stabilité de la planification, un ajustement réussi et la capacité de changer la trajectoire de planification pendant son exécution.

Image n ° 6
L'analyse de phase par moyennage permet de quantifier la contribution relative des moments aérodynamiques et inertiels à la dynamique de glissement.
Des équations n ° 5, il résulte que les forces aérodynamiques et la distribution de masse changeante affectent l'orientation du corps. La contribution aérodynamique ( 6a ) augmente avec le temps à mesure que la vitesse augmente, tandis que la contribution inertielle ( 6b ) reste constante. Les deux moments sont périodiques et seul le moment de tangage montre une moyenne de phase non nulle.
Initialement, les moments d'inertie prédominent près des axes de tangage et de roulis, mais au cours d'un cycle semblable à une vague, leur contribution diminue rapidement. Les moments de lacet d'inertie, en règle générale, sont d'un ordre de grandeur plus grand que les moments de lacet aérodynamique et sont plus grands que les moments d'inertie autour d'autres axes. Les moments d'inertie de lacet se produisent en raison d'une onde horizontale de grande amplitude et d'un large corps en forme de S. Ce résultat suggère que les cerfs-volants volants peuvent utiliser la rotation inertielle comme mécanisme de manœuvre.
Pour une connaissance plus détaillée des nuances de l'étude, je vous recommande de consulter le rapport des scientifiques et des éléments supplémentaires .
Et ceux qui souhaitent se familiariser avec le logiciel utilisé pour analyser la planification d'un cerf-volant volant peuvent suivre ce lien .
Épilogue
Dans cette étude, les chercheurs ont utilisé les dernières techniques de capture de mouvement et de modélisation 3D pour créer un modèle anatomiquement précis d'un serpent volant.
Comprendre la dynamique du vol d'un oiseau était autrefois également difficile, mais cela ne déroutait pas les scientifiques autant qu'un cerf-volant volant. Dans la nature, il n'y a pas tant d'exemples de vols sans ailes, et tous sont associés à l'utilisation de mécanismes non standard qui permettent à l'animal de planifier et de ne pas tomber comme une pierre au sol.
Dans le cas des serpents volants, l'ondulation observée dans le mouvement des serpents rampants et flottants joue un rôle très important. Un mécanisme supplémentaire pour stabiliser la planification est la correction de l'angle dorsoventral de la flexion du corps. En combinant ces éléments ensemble, les cerfs-volants volants sont capables de voler d'arbre en arbre, connaissant exactement le lieu de plantation future.
Les auteurs de ce travail croient que leurs données nous ont non seulement permis de mieux comprendre les habitudes des serpents d'arbres décorés, mais aussi de trouver une inspiration supplémentaire pour créer des robots ressemblant à des serpents. Oui, de tels robots existent déjà. Ils rampent, peuvent se déplacer sur des surfaces difficiles et pénétrer dans des endroits difficiles d'accès, mais peuvent-ils voler?
Avec de telles considérations, notre monde ressemblera bientôt à la ville des voitures de la matrice, où des créatures robotiques extrêmement inhabituelles (et légèrement effrayantes) rampaient le long des murs, dont le but était difficile à comprendre. Le désir d'une personne de créer une version robotisée de tout ce qui l'entoure ne peut pas être étouffé. C'est notre nature - de tout comprendre, de tout savoir, de pouvoir créer ce que la nature a fait magnifiquement avant nous. S'il y a beaucoup plus d'avantages que de mal des serpents robotiques, des araignées, des chiens et d'autres animaux robotiques, une telle recherche est pleinement justifiée.
Merci d'avoir regardé, restez curieux et passez un excellent week-end à tous, les gars!
Vendredi off-top:
, .
, .
Off-top 2.0:
, :)
, :)
Un peu de publicité
Merci de rester avec nous. Aimez-vous nos articles? Vous voulez voir du contenu plus intéressant? Soutenez-nous en passant une commande ou en recommandant à des amis, VPS cloud pour les développeurs à partir de 4,99 $ , un analogue unique des serveurs d'entrée de gamme, qui a été inventé par nous pour vous: Toute la vérité sur VPS (KVM) E5-2697 v3 (6 cœurs) 10 Go DDR4 480 Go SSD 1 Gbps à partir de 19 $ ou comment diviser le serveur correctement? (les options sont disponibles avec RAID1 et RAID10, jusqu'à 24 cœurs et jusqu'à 40 Go de DDR4).
Dell R730xd 2 fois moins cher au centre de données Equinix Tier IV à Amsterdam? Nous avons seulement 2 x Intel TetraDeca-Core Xeon 2x E5-2697v3 2.6GHz 14C 64GB DDR4 4x960GB SSD 1Gbps 100 TV à partir de 199 $ aux Pays-Bas!Dell R420 - 2x E5-2430 2,2 Ghz 6C 128 Go DDR3 2x960 Go SSD 1 Gbps 100 To - à partir de 99 $! Lisez à propos de Comment construire l'infrastructure de bldg. classe avec l'utilisation de serveurs Dell R730xd E5-2650 v4 coûtant 9000 euros pour un sou?