AES est la norme de cryptage américaine. Partie IV

Dans cette partie IV, nous complétons la description du chiffrement AES-128. Pour les lecteurs qui ne sont pas familiers avec les parties précédentes de l'ouvrage, j'expliquerai que le matériel est présenté à des fins pédagogiques et cela impose un certain nombre de caractéristiques (détails, exemples numériques, fondements mathématiques, etc.) Il ne s'agit pas seulement de se familiariser avec la norme , et l'utilisation du matériel présenté pour le développement d'algorithmes de cryptage et de décryptage (en l'absence de clé). Les auteurs de nombreuses publications bien connues en ligne (et hors ligne) ne se sont pas fixé de tels objectifs, ce qui rend ces publications peu utiles à nos fins.



Le processus inverse de cryptage est appelé décryptage de message. Pour déchiffrer (avec une clé) les textes chiffrés (PCT), une table de substitution inverse et des clés rondes sont créées, qui sont utilisées dans l'ordre inverse par rapport au schéma de cryptage, mais similaire au processus de cryptage.

Décrypter les messages AES

La liste des opérations de déchiffrement d'un message reste la même que pour le chiffrement. Plus de détails sur les opérations peuvent être trouvés ici . Il s'agit d'un principe assez général des chiffrements - une seule implémentation matérielle pour le chiffrement et le déchiffrement, qui est fournie par des ensembles des mêmes fonctions pour les deux processus. Seuls le texte source et la séquence de soumission des clés sont modifiés.



Le processus de déchiffrement des messages est mis en œuvre comme une séquence de transformations inverses (inverses) utilisées pour le chiffrement, dans l'ordre inverse de leur séquence pendant le chiffrement. Il est également évident que les touches rondes sont utilisées dans l'ordre approprié: d'abord, la clé reçue en dernier, puis l'avant-dernière touche, et ainsi de suite jusqu'à la première touche ronde.



Tous les noms de transformation restent les mêmes, mais sont préfixés par Inv. Nous les considérerons dans le même ordre que précédemment. Le chiffrement AES permet deux options de déchiffrement, inverse et direct, qui sont décrites en détail ci-dessous.

Option de déchiffrement inversé

Le déchiffrement inversé d'un message est un processus naturel d'inversion du processus de chiffrement.



L'opération AddRoundKey reste la même (inchangée) S + Ki pour les 16 octets de l'état comme elle l'a fait lors du chiffrement du message, c'est-à-dire est l'inverse de lui-même. Cela est dû au fait que la logique XOR est utilisée dans l'opération et que les octets sont représentables en nombres binaires.

La clé du dernier tour est simplement ajoutée (résumée) au message chiffré.



InvSubBytes. L'essence de cette transformation n'a pas changé, c'est-à-dire que chaque octet du message en cours de conversion est remplacé par un autre extrait de la table (S ^-1-block) remplacement. Bien entendu, la table de substitution est ici différente. L'octet {x, y} est remplacé par l'octet de Inv S (x, y) selon le même principe: x - ligne de table, y - sa colonne. L'octet de remplacement est extrait de la cellule à l'intersection de la ligne (x) et de la colonne (y) de la table Inv S (x, y).



Comme précédemment, la taille de la table est de 16 × 16 = 256 octets, chacun étant obtenu par multiplication et soustraction de matrice vectorielle (transformation affine) du produit du vecteur de décalage C.Dans les champs binaires, les opérations d'addition et de soustraction sont équivalentes, le vecteur C peut donc être simplement ajouté à produit. Le tableau InvSubBytes est illustré ci-dessous. Le nœud de substitutions S ^-1 spécifié est présenté dans le tableau 1 suivant, les valeurs sont données au format hexadécimal:



Tableau 1. Tableau des substitutions du bloc inverse S ^-1







Le tableau montre des exemples de remplacement de deux octets 4A → 5C et 9F → 6E remplis de vert.



InvShiftRows. Cette transformation décale les lignes du tableau (le carré d'état) vers la droite (dans le sens opposé au décalage d'origine). La valeur de décalage pour chaque ligne reste la même: la première ligne (du haut) n'est pas décalée c0 = 0, la seconde est décalée de c1 = 1, la suivante est décalée de c2 = 2 et la dernière est c3 = 3 positions (cellules). Les valeurs c0, c1, c2, c3 ont été données dans le tableau et dans la figure précédemment pour le premier cycle de conversion de message.







Le résultat d'une telle multiplication dans la représentation scalaire est:



S'0C = ({0l} · S0C) {({0b} · S1C) ⊕ ({0d} · S2C) ⊕ ({09} · S3C);

S'1C = ({09} S0C) ⊕ ({0l} S1C) ⊕ ({0b} S2C) ⊕ ({0d} S3C);

S'2C = ({0d} S0C) ⊕ ({09} S1C) ⊕ ({0l} S2C) ⊕ ({0b} S3C);

S'3C = ({0b} S0C) ⊕ ({0d} S1C) ⊕ ({09} S2C) ⊕ ({0l} S3C).





Pour obtenir des informations informatiques à partir de PC, l'algorithme de décryptage utilise les mêmes valeurs de paramètres que celles utilisées dans le processus de cryptage. Pour la formation de la clé étendue, les règles restent les mêmes.

Option de déchiffrement direct

Les particularités de l'algorithme de décryptage pour certaines transformations inverses permettent de conserver la même séquence d'opérations que dans l'algorithme de cryptage, mais certaines valeurs de paramètres nécessitent des modifications. Tout d'abord, nous parlons de la clé (son déroulement).



La recherche a montré que l'ordre des fonctions SubBytes () et ShiftRows () ne change pas la valeur du résultat, c'est-à-dire que ces fonctions sont permutables (elles commutent). Cette position (propriété) est également vraie pour les fonctions InvSubBytes (), InvShiftRows (). Ce schéma est facile à expliquer. Le fait est que les deux fonctions fonctionnent sur des octets entiers et que les décalages sont effectués par un multiple entier d'un octet et ne modifient pas la valeur des octets eux-mêmes.

Notez ce qui suit à propos de l'opération MixColumns (). Il est linéaire aux octets d'entrée (données).



InvMixColumns (State XOR Round Key) = InvMixColumns (State) XOR

InvMixColumns (Round Key).

Ces caractéristiques des fonctions (propriétés) permettent de changer l'ordre de leur application, c'est-à-dire

InvSubBytes (InvShiftRows ()) = InvShiftRows (InvSubBytes ()).

AddRoundKey (InvMixColumns ()) = InvMixColumns (AddRoundKey ()),

mais à condition que les colonnes (mots de 32 bits) de la clé de déchiffrement étendue aient été précédemment passées via la fonction

InvMixColumns ().



Ce qui précède signifie que le mode de décryptage du PC peut être rendu effectif en préservant l'ordre d'utilisation des fonctions adoptées pour le cryptage. Evidemment, dans ce cas, les coûts de mise en œuvre matérielle et logicielle du chiffrement sont considérablement réduits. Les modifications concernent uniquement la procédure de génération du déploiement de clé.



Dans la fonction InvMixColumns (), vous devez convertir le type de la variable, le paramètre d'entrée de la fonction est un tableau d'octets bidimensionnel (carré) et la clé développée est formée comme un tableau linéaire (chaîne) de mots de 32 bits. Pour cette raison, il est nécessaire d'effectuer une correspondance de type avec le carré.



Montrons, à l'aide de l'exemple d'une transformation en 2 tours, deux versions équivalentes de la procédure de déchiffrement RIJNDAEL. La première option est l'inverse habituel de la fonction de cryptage. La deuxième option est obtenue à partir de la première en modifiant l'ordre des opérations en trois paires de transformations

InvShi ftRows () → InvSubBytes () 2 fois et

AddRoundKey () → InvMixColumns () 1 fois.



Le résultat de la transformation est enregistré lors du passage de l'original à la

séquence d'opérations inverse dans les paires spécifiées.



À partir du tableau, nous voyons que la procédure de chiffrement et la deuxième variante de la procédure de déchiffrement coïncident jusqu'à l'ordre d'utilisation des clés rondes (lors de l'exécution des opérations AddRoundKey), des tables de remplacement (lors de l'exécution des opérations SubBytes () et InvSubBytes ()) et des matrices de transformation (lors de l'exécution des MixColumns ( ) et InvMixColumns ()).



Tableau 2 - Séquence des transformations dans la version à deux tours de RIJNDAEL







Un résultat similaire s'avère vrai pour n'importe quel nombre de tours.

Récupération d'une clé de chiffrement à l'aide de la dernière sous-clé

Génération de clés de chiffrement AES rondes. Le programme de clé pour générer des clés rondes à partir d'une clé de chiffrement d'origine de 128 bits est une fonction récursive. Cette fonction est décrite en détail ici . Les conditions initiales de son lancement sont les 4 premiers mots de 4 octets de la clé (4 × 32 bits), soit W [0], W [1], W [2], W [3]. Formulons le problème de la récupération de cette clé de chiffrement de 128 bits comme suit:



Soit les composants de la clé ronde 10 ronde W [43], W [42], W [41], W [40].

Il est nécessaire de récupérer la clé de chiffrement complète avec uniquement cette clé ronde.

Il convient de considérer d'abord la solution du problème sur des données numériques. Prenons l'exemple numérique donné dans FIPS PUB 197 comme base.... Le tableau 3 contient la clé du tour 10.



La procédure de génération de clés rondes est organisée de telle manière qu'elle permet un mouvement vers l'avant (dépliage de la clé) le long d'un certain nombre de valeurs clés précédentes. Pour reculer à partir d'un point d'une série de valeurs, il est nécessaire d'avoir les données initiales du processus de calcul à ce point de retour. Que le point de retour soit la dernière étape du dernier 10e tour, à savoir, quatre mots de 4 octets de la 10e clé ronde Nk = Nb = 4 sont connus.



Tableau 3 - clé de 128 bits du 10e tour de l'algorithme de chiffrement AES En







outre, les résultats et les actions de l'algorithme clé de récupération sont placés pour commodité dans le tableau 4, qui est similaire à une table de génération de clé (en quelque sorte renversée).



Tableau 4 - Récupération de la clé de chiffrement à partir de la clé connue du 10e tour







Explications pour le tableau 4. Les nombres ronds sont comptés dans l'ordre inverse du 10 au 1er. Trois colonnes (3, 8, 9) du tableau contiennent des clés prêtes à l'emploi avec des numéros courants différents en fonction du numéro de ligne i. Les cellules restantes contiennent des données auxiliaires pour les calculs intermédiaires. Ainsi, la valeur de la clé W [i] apparaît dans le tableau trois fois dans trois colonnes.



Les colonnes 1 et 2 sont le nombre r du tour et le nombre ordinal i du mot clé de 4 octets. Le dernier mot de ce type pendant le cryptage a le numéro i = 43. Dans le tableau, nous l'écrivons dans la ligne supérieure de la colonne de droite (9). Les nombres i des lignes du tableau sont décroissants et dans la colonne 9 ils correspondent aux mots de la clé W [i]. La 8ème colonne contient le mot W [i - Nk] de la clé avec un nombre réduit W [43 - 4] = W [39], et la 3ème colonne - le mot clé W [i - 1] = W [42], précédent W [i] = W [43].



La signification du mot W [39] dans la 8ème colonne est inconnue et nous la trouvons à partir des données initiales en utilisant la formule:







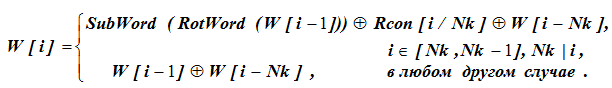
Pour les calculs de formule, les conditions de sélection de la ligne de formule sont d'abord vérifiées. Pour W [43], i = 43 et Nk ne divise pas complètement la valeur 43, c'est-à-dire que pour i = 43 la valeur de W [i] est déterminée par la ligne du bas de la formule: W [43] = W [42] W [39]. Ici, pour les valeurs données de W [42] et W [43], le dernier terme W [39] n'est pas défini.

Alors W [39] = W [43] W [42] = b6630ca6 - e13f0cc8.



En arithmétique binaire mod2, les opérations d'addition et de soustraction sont équivalentes, donc les calculs bit à bit pour chacun des 4 octets du mot-clé W [39] prennent la forme (Tableau 5):

Tableau 5 - Calculs d'octets du mot-clé W [39].







Ainsi, la valeur du mot clé W [39] = 575c006e a été trouvée. Nous transférons cette valeur à la 3ème colonne, à la ligne i = 40 et à la 9ème colonne à la ligne i = 39. Les



calculs de la ligne i = 40 sont effectués comme lors du développement de la clé.



Le mot inconnu W [i - Nk] = W [40 –Nk] = W [i = 36] doit être déterminé comme dans le cas précédent par la différence W [36] = W [40] 7 colonne de la ligne 40.



À son tour, la valeur en 7- La ème colonne de la ligne 40 est formée comme la somme (OR) des 5ème et 6ème colonnes. La valeur de la 5e colonne est obtenue à partir de W [39] après un décalage cyclique RotWord (4e colonne) et une opération de remplacement de sous-mot (5e colonne).



Les résultats de ces actions prennent la forme

RotWord (575c006e) = 5c006e57; Sous-mot (5c006e57) = 4a639f5b.



La valeur de la 6ème colonne est obtenue sous forme de constante

Rcon [j = i / Nk] = Rcon [j = 40/4] = 2 ^j-1 = 2 ⁹ .



Cette constante est représentée par un octet hexadécimal

2 ⁹ ≈100000000 = x ⁹ , mais il n'y en a pas dans le champ GF (2 ⁸ ): vous devez trouver le reste de la division par un polynôme irréductible, c'est-à-dire

$$$^9 : ^8+ ^4+ ^3+ + 1= ^5+ ^4+ ^2+ = 00110110 = 36.$



Après avoir inclus la constante dans le mot-clé, nous avons

Rcon [j = 40 / Nk] = 36000000 (6e colonne). La valeur de la 7e colonne est obtenue comme suit (7e colonne) = (5e colonne) ⊕ (6e colonne) = 4a639f5b⊕36000000 = 7c639f5b.



Et enfin, pour

W [36] = W [40] (7ème colonne de la ligne 40) = d014f9a8 7c639f5b = ac7766f3.



D'autres calculs par analogie mènent au résultat final - la clé de chiffrement.

Il y a plus d'informations sur les fonctions w et RotWord, Rcon et SubWord. Supposons que nous notions Kr [j] - le j-ième octet de la r-ième clé ronde et w [i] comme dans la documentation.



On obtient: Kr = (w [Nk ∙ r], w [Nk ∙ r + 1], · · ·, w [Nk ∙ r + Nk - 1]).



Pour différents i, nous avons les relations suivantes



pour i ≠ 0 mod Nk, Nk ≤ i <Nb ∙ (Nr +1), w [i] = w [i - Nk] xor w [i - 1] et

pour i = 0 mod Nk, w [i] = w [i - Nk] xor SubWord (RotWord (w [i - 1])) xorRcon [i / Nk].



Par conséquent, pour i ≠ 0modNk, Nk 0≤i <Nb ∙ (Nr + 1) –Nk, w [i] = w [i + Nk] xor w [i + Nk - 1] et pour i = 0modNk, w [i] = w [i + Nk] xorSubWord (RotWord (w [i + Nk - 1])) xorRcon [i + Nk / Nk]

Avec AES-256, vous devez ajouter une opération Subword lorsque i est comparable à 4mod Nk. Il est donc possible de déduire la clé précédente de la sous-clé finale et d'obtenir pas à pas la valeur K0 de la clé de chiffrement.



Les fondements mathématiques du chiffrement AES - 128 sont assez complets et détaillés ici .



Passons au mappage de champ field: GF (2 ⁸ ) → GF (2 ⁸ ); x → x ² + x. L'image de cette carte

1 = Im (l) a la dimension dim GF (2) (1) = 7.



Equation x² + x = θ, où θ 1 a deux solutions différentes (racines de l'équation) 1, 2є GF (2 ⁸ ).



Par le théorème de Vieta, x1⊕x2 = 1, la somme des racines est égale au coefficient de l'équation en x ² avec le signe opposé, et le produit des racines x1⊗x2 = θ est égal au terme libre de l'équation (dans notre équation avec le signe opposé).



On sait que dans l'arithmétique des champs binaires, les opérations d'addition et de soustraction d'éléments mod2 sont équivalentes.







Ainsi, les racines de l'équation sont liées par le rapport x2 = x1⊕1, puisque le coefficient en x dans l'équation est 1. Cela signifie que dans la représentation décimale des éléments de champ avec leur ordre lexicographique, ils sont situés l'un après l'autre, ne différant que d'un.



Donc, pour x = 0 et x = 1 et pour x = 2 et x = 3, nous obtenons:







Les résultats (images) de la cartographie dans les paires réduites (0, 1); (2, 3) complètement coïncidé, c'est-à-dire deux types correspondent à une image. Par conséquent, la cardinalité de l'image est deux fois inférieure à la cardinalité de la pré-image et sa dimension de ses éléments est de 7.



Le produit des paires de racines, c'est-à-dire le terme libre d'une équation quadratique est commodément déterminé par la représentation en puissance des éléments du champ (images inverses). Dans ce cas, les exposants sont additionnés mod255, c'est-à-dire modulo l'ordre du groupe multiplicatif du champ GF (2 ⁸ ).