
L'optimisation en entreprise est dans la très grande majorité des cas associée à l'utilisation de la méthode de programmation linéaire. La méthode est assez simple. De plus, il existe un théorème sur l'existence et l'unicité de la solution.
Cependant, dans la pratique, tout n'est pas entièrement simple.
Le premier problème est la non-linéarité des conditions du monde réel. Pour que la méthode de programmation linéaire soit applicable, ils doivent être linéarisés. Il existe des moyens de définir de manière plausible la non-linéarité au moyen d'équations linéaires et d'inégalités en introduisant de nouvelles variables, en définissant des coefficients de pondération, etc. Lors de la résolution des problèmes de production dans ce cas, il est nécessaire d'opérer avec un grand nombre de variables et, par conséquent, d'équations (inégalités).
Dans la théorie de la résolution de problèmes extrêmes, il existe un théorème sur la stabilité des solutions aux problèmes de programmation linéaire. Selon lui, la solution n'est stable que si le domaine du problème est convexe. Avec un grand nombre de variables et d'inégalités, il n'est pas possible d'établir si le domaine du problème est convexe. De plus, la probabilité de non-convexité est élevée.
Si le problème n'est pas stable, alors en fonction du point de départ de la traversée des sommets, des résultats différents seront obtenus.
Deuxième problème- restriction de la variable par le bas (x> h> 0). Toute implémentation d'une méthode de programmation linéaire fournira toujours une valeur x non nulle. Si x est exactement égal à h, cela signifie que la valeur de la variable x doit être essentiellement zéro. En pratique, ces volumes «fictifs» (méthode kurtosis) sont dispersés sur des variables «significatives». La conséquence de cette pratique est l'érosion du concept de solution optimale, ce qui est particulièrement important si une telle solution est l'une des nombreuses dans la chaîne de décision.
Le troisième problème est celui de la gestion. La méthode de programmation linéaire ne donne qu'un seul résultat. Et comment regarder des résultats proches de l'optimum? Par exemple, dans la solution résultante, la note du fournisseur est mauvaise. Comment comprendre s'il existe des solutions proches, mais pour des fournisseurs fiables.
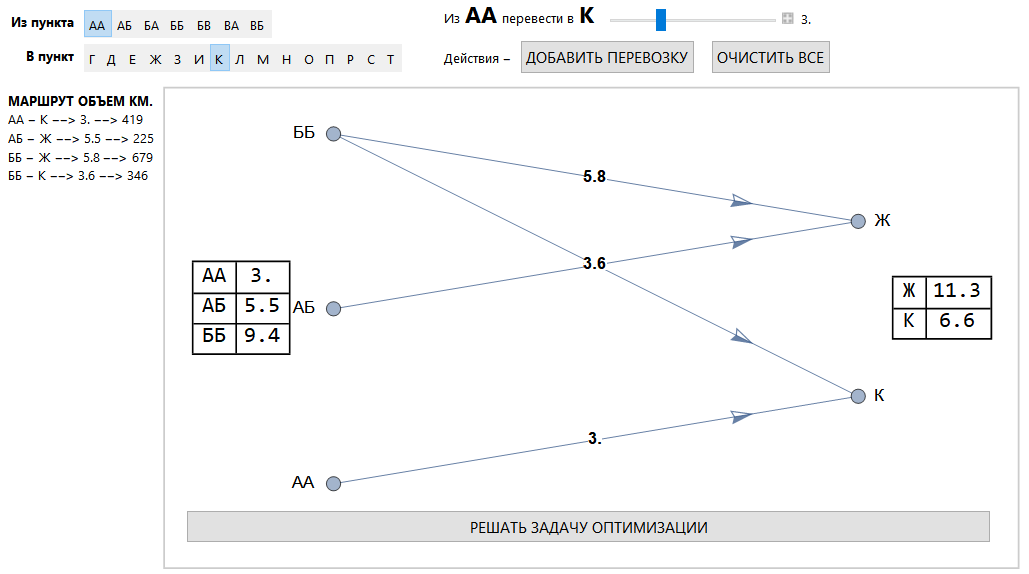
Tâche de transport
L'exemple correspond à un problème de programmation linéaire de transport.
Il y a 5 transporteurs (la tâche a été fixée pour le transport du charbon), qui ont deux calculs tarifaires. Les limites tarifaires et les tarifs eux-mêmes peuvent être modifiés (ils sont définis de manière paramétrique).

Le transport est spécifié en tant que point à point (selon la méthode acceptée pour le transport du charbon) et en volume.
Vue générale de l'interface.

Zone d'affectation de transport.
Méthode de solution de cluster
Au lieu d'un problème de programmation linéaire, un groupe de problèmes est résolu, dont le nombre correspond à toutes les combinaisons possibles de tarifs. Dans l'envoi ci-dessus, il y en a 127 (deuxième valeur dans le rectangle supérieur gauche).

Les solutions optimales sont sélectionnées parmi l'ensemble des problèmes corrects restants. Chaque tâche fournit une solution optimale pour une combinaison spécifique de tarifs. Les solutions présentées ci-dessus constituent une certaine fourchette de maximums.
Pourquoi la méthode de cluster est bonne:
- il y a une compréhension de la stabilité de la solution.
- il n'y a pas de volumes «fictifs» pour les variables bornées par le bas, car il y aura une autre combinaison où une telle condition est absente (puisqu'une telle variable est absente).
- des conditions subjectives (notes, préférences) peuvent être introduites en utilisant la méthode de programmation linéaire standard.
Avec un plus grand nombre d'expéditions, nous avons l'image suivante (fragment).
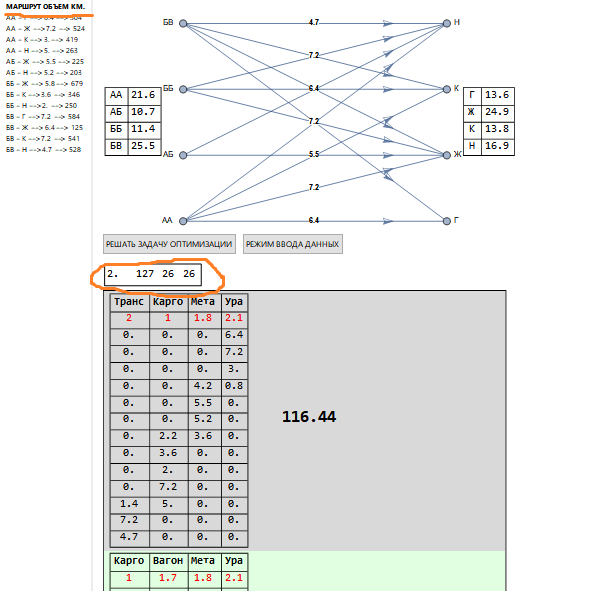
Dans le coin supérieur gauche, dans le rectangle au-dessus des solutions (surligné en orange), d'autres valeurs sont indiquées qu'avant: 127 - combinaisons (comme précédemment, qui est liée à la structure des barèmes tarifaires), 26 - correspond au nombre de problèmes corrects restants qui sont en cours de résolution. Le tarif utilisé est indiqué en rouge sous le nom du transporteur, et les colonnes de transport correspondent à la liste des itinéraires (soulignée en orange).
Il est important de noter que la méthode utilisée vous permet de comprendre le résultat, d'évaluer des solutions similaires et d'utiliser votre expérience professionnelle lors du choix d'alternatives, en tenant compte des subtilités de la gestion d'une entreprise particulière.