- Bonjour à tous, je m'appelle Rishat. Je travaille sur la qualité de la recherche Yandex depuis près de trois ans. Mais aujourd'hui, je ne veux pas parler de travail, mais de ce que je fais pendant mon temps libre. Je suis engagé dans l'informatique quantique, mais en fait - une variété de modèles de calcul, y compris des modèles quantiques.
L'informatique quantique est actuellement un domaine intéressant. Beaucoup d'efforts y sont investis, beaucoup a été fait. Dans mon rapport, j'essaierai d'intéresser certains d'entre vous. Peut-être qu'il y a un ingénieur ML cool parmi vous qui veut faire de l'apprentissage automatique quantique, ou simplement un algorithme fort qui peut investir dans cette direction. Ce sera formidable car l'avenir arrive bientôt.
Je dois dire tout de suite que je ne suis pas physicien. Il y a sûrement des gens parmi vous qui comprennent tous ces processus en physique plus que moi. Par conséquent, je ne dirai presque rien sur la physique.
J'attends de vous que vous vous souveniez un peu de l'algèbre, que vous vous rappeliez ce qu'est un vecteur et comment multiplier un vecteur par une matrice.

Comment mon rapport sera-t-il structuré? Tout d'abord, nous parlerons un peu d'histoire, d'où tout vient pour regarder l'avenir avec confiance. Ensuite, nous verrons où cela peut être appliqué, quel est l'état actuel, s'il est possible de faire quelque chose avec vos mains maintenant. Nous allons écrire le premier programme Python qui peut être exécuté sur un ordinateur quantique. Et puis, en prime, je vais vous montrer quelques exemples d'algorithmes dans lesquels l'informatique quantique permet d'obtenir des performances incomparablement meilleures par rapport aux algorithmes classiques.

Comment tout cela a-t-il commencé? De ce jeune homme. C'est Alan Turing, il peut être appelé sans aucun doute le père de l'informatique ou de l'informatique, celui par lequel nous vivons tous maintenant, gagnons de l'argent. Dans les années 1930, Turing a proposé un modèle de calcul que nous appellerions maintenant un ordinateur programmable. Mais est-ce que quelqu'un reconnaîtra cette personne?

Plus difficile. Son nom de famille vient très souvent à côté du nom de famille de Turing. C'est Alonzo Church, il a également traité des problèmes de calculabilité, et même un peu avant que Turing ne propose ses propres modèles de calcul. Mais le travail de Turing est devenu plus populaire. Et en général, Church a été à un moment donné le conseiller scientifique de Turing. Pris ensemble, leurs noms sont généralement associés à cette thèse.
La thèse de Church-Turing dit: tout processus peut être efficacement modelé sur une machine de Turing. Nous sommes à la fin des années 30 - au début des années 40, et tout est très bon. Depuis environ 30 ans, tout va très bien, jusqu'à ce que ces deux personnes apparaissent. Quelqu'un les connaît-il?

C'est déjà les années 70, très proche du présent. Leurs noms de famille se retrouvent souvent dans les cours de cryptographie. Ce sont Robert Nightingale et Volker Strassen. Ces deux personnes sont connues pour avoir mis au point un algorithme probabiliste permettant de vérifier un nombre par souci de simplicité, le test Solovey-Strassen.
Et c'est un point très important pour nous, car jusqu'à présent nous disions que tout processus algorithmique peut être modélisé sur une machine de Turing. Mais maintenant, il s'avère que leur algorithme ne peut pas être modélisé. C'est probabiliste, il n'y a rien de tel dans la machine de Turing.
J'ai dû faire une solution rapide et dire que tout processus peut être modélisé sur une machine probabiliste de Turing. Ce n'est plus très cool, c'est sûr que l'un de vous a une pincée dans la poitrine. Vous avez pensé: comment ça? Maintenant on dit "probabiliste", dans dix ans on découvrira autre chose, il faudra corriger autre chose. Ce n'est pas très agréable. Mais vous et moi, bien sûr, ne sommes pas seuls.

Il y avait un autre jeune homme - David Deutsch. Et lui aussi se demandait: comment cela? Comment vivre? Il est physicien de formation, a consacré toute sa vie à la physique. Et j'ai décidé d'aborder ce problème du point de vue de la physique. Il a dit: essayons de justifier, obtenons quelque chose pour que la nature elle-même nous dise que c'est exactement le cas. Et la nature a déjà dit alors (et nous croyons toujours) que c'est de la mécanique quantique. Nous avons donc commencé à chercher une réponse en mécanique quantique. Et c'est avec David Deutsch, avec ses premiers algorithmes, que l'informatique quantique a commencé.
C'est une si petite excursion dans l'histoire pour que vous compreniez: cela n'est pas sorti de nulle part. Dans ce domaine, il y a de vrais problèmes, théoriques, bien sûr, qui tourmentent les gens qui ont tout commencé.
Mais tout est-il seulement au niveau de la théorie? Dans l'ensemble, du point de vue des mathématiques, il n'y a plus de problèmes. Mathématiquement, nous savons tout sur le fonctionnement d'un ordinateur quantique. Maintenant, il existe déjà de vrais ordinateurs quantiques de différentes configurations, fonctionnant de différentes manières. Et c'est, dans l'ensemble, un défi d'ingénierie.
Par exemple, dans notre institut, nous avons tout un département qui s'occupe de l'informatique quantique. Il y a des mathématiciens et des physiciens. Les physiciens sont désormais très étroitement engagés dans le problème du stockage à long terme des informations quantiques. C'est très similaire à nos disques durs, mais nous voulons que les informations quantiques y soient stockées.

Quelles sont les utilisations de toute cette économie? Bien sûr, la première chose qui me vient à l'esprit est la modélisation des processus, car le monde est de la mécanique quantique. Et si nous utilisons un ordinateur quantique pour simuler des processus, des réactions chimiques ou autre, ce sera beaucoup moins cher en calcul.
La deuxième et très grande section, à laquelle de nombreux efforts sont désormais consacrés, est l'apprentissage quantique. Il y a un grand espoir que l'informatique quantique aidera à accélérer les processus d'apprentissage eux-mêmes et à améliorer les algorithmes. Il y a beaucoup de travail ici. Maintenant, par exemple, notre groupe quantique travaille avec un scientifique chinois. C'est un ingénieur ML très fort, et nous avons un peu de biais quantique, essayant de trouver quelque chose ensemble.
La troisième chose était un peu hype il y a quelques mois. Maintenant, peut-être que le battage médiatique est déjà endormi, mais il existe même toute une blockchain quantique. Il a été inventé par mon bon ami et mon grand ami. C'est moi, dis-je un peu fièrement.
Mais nous n'avons pas d'ordinateur quantique. Malheureusement, nous ne pouvons pas rentrer à la maison et exécuter des programmes aussi facilement que nous programmons en Python.
Que faire? Je réfléchissais à ce qu'il fallait faire pendant ma troisième année lorsque j'écrivais mon premier mémoire. J'écrivais un émulateur d'informatique quantique. Bien sûr, tout le monde écrit des émulateurs et tout le monde les utilise d'une manière ou d'une autre. Au cours de ma quatrième année, j'ai écrit un émulateur qui simule les interférences, les bruits, etc. Et puis je me suis ennuyé.
J'ai essayé de chercher dans un moteur de recherche et j'ai réalisé qu'il existe de nombreux émulateurs. Voici quelques liens, ils sont assez simples et intéressants:
- github.com/quantumlib/Cirq
- github.com/artiste-qb-net/qubiter
- code.google.com/archive/p/pyqu
- qiskit.org
Mais je veux m'arrêter à qiskit. Il est spécial, se démarque de tout. Que?
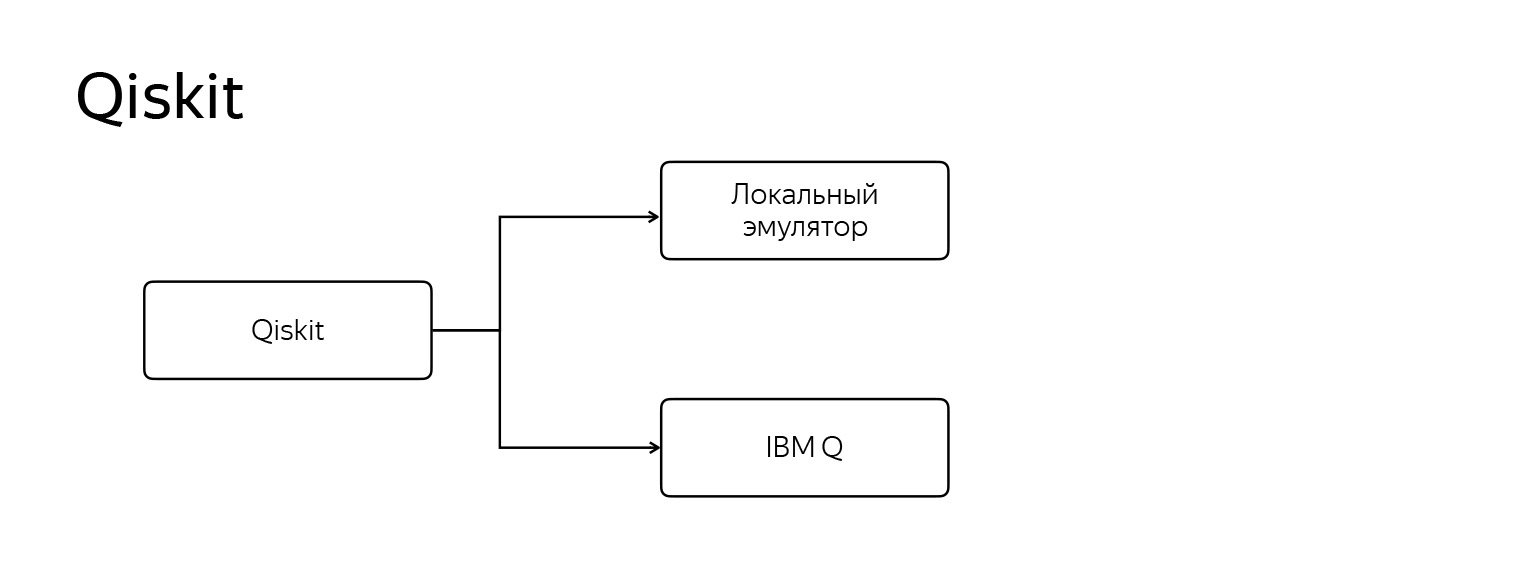
Cela fonctionne selon deux modes. Le premier est, comme tout le monde, un émulateur local régulier. La seconde consiste à exécuter votre programme sur un véritable ordinateur quantique IBM Q, qui ressemble à ceci.

Maintenant, c'est un tonneau entier dans lequel une température extrêmement basse est maintenue - environ trois millikelvin. Il fait très froid. Et IBM offre la capacité basée sur le cloud de se connecter et d'exécuter votre code directement sur cette machine.
Bien sûr, il compile les commandes et ainsi de suite d'une manière spéciale. Comment ça marche? Il existe plusieurs installations d'un tel ordinateur pour un accès général. L'un d'eux est 5 qubits, il y a 15 qubits, 16 qubits, même 20 qubits sont disponibles pour nous. Il s'agit d'environ 20 bits d'informations classiques ordinaires, mais déjà quelque chose.
Ici, c'est sûr, beaucoup d'entre vous pensent: ça y est, je le veux! Mais vous devez vous rappeler un peu de maths. Un peu d'algèbre, mais juste un peu, comme je l'ai promis.
Pour commencer à programmer sur un ordinateur quantique, vous devez comprendre ce qu'est un qubit. C'est juste un vecteur dans un espace vectoriel 2D. Mais puisque nous parlons d'espaces vectoriels, ils ont une base.

La base ressemble à quelque chose comme ça. Il y a deux colonnes vectorielles et une base unitaire, standard, dans les cours d'algèbre, elle est désignée comme suit:
et
... Et il y a une notation standard dans la notation de Dirac, entre ces crochets angulaires.
Autrement dit, pour que vous ne soyez pas confus, je continuerai à raccourcir comme ça.
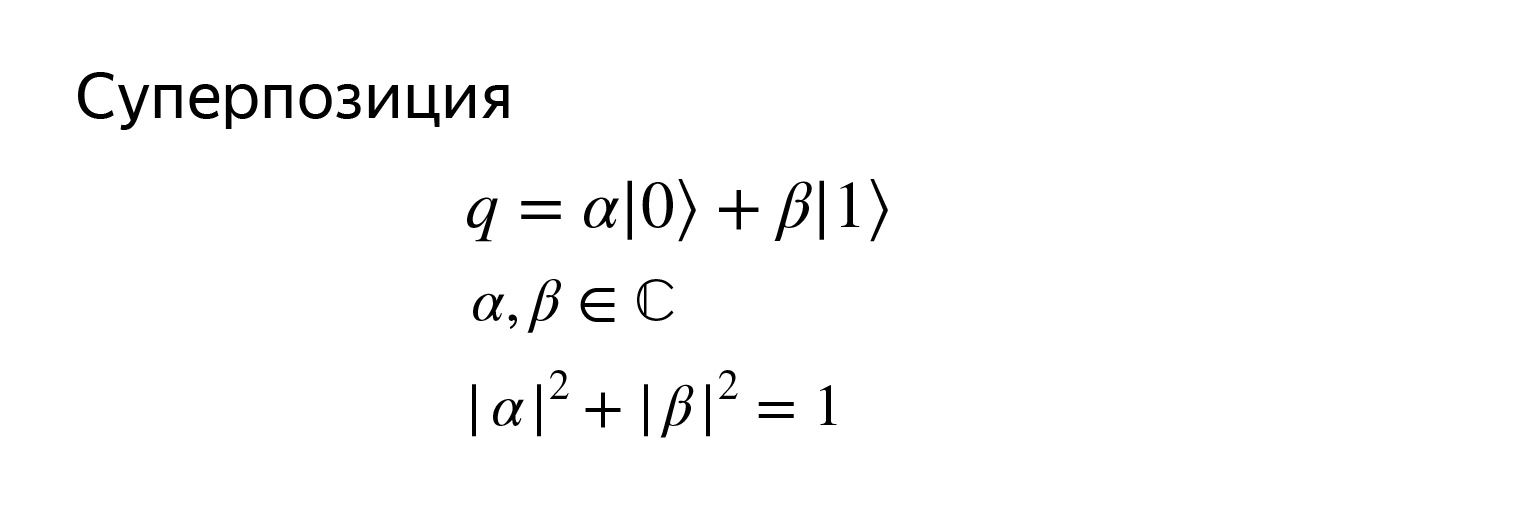
Et comme il s'agit d'un vecteur, son état peut s'écrire ainsi. Un qubit q est une superposition de deux vecteurs de base, où α et β sont des nombres complexes, mais pas absolument des nombres, mais de sorte que la somme des modules de leurs carrés soit égale à un.
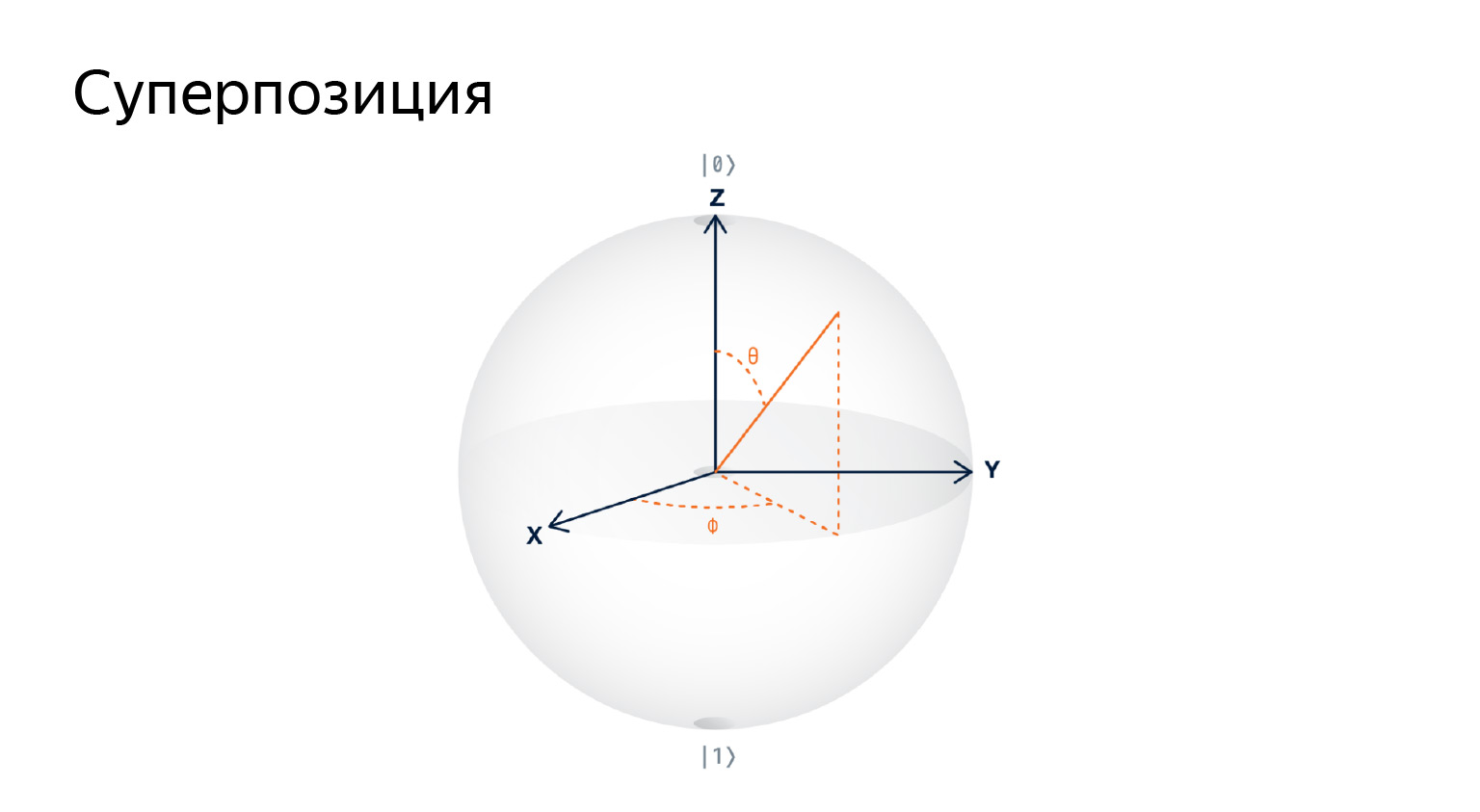
Si nous essayons de dessiner cette chose, nous obtenons qu'un qubit est un vecteur sur une sphère tridimensionnelle. Une quantité infinie d'informations peut être stockée dans un qubit, car ce n'est qu'un vecteur, dont il existe une quantité infinie.
Vous n'avez pas besoin de prêter attention à l'image, c'est juste une technique de visualisation pour attirer l'attention.
Nous avons parlé de qubits. Plus important encore, un qubit est un vecteur. Vecteur dans un espace vectoriel complexe. Que pouvez-vous en faire?
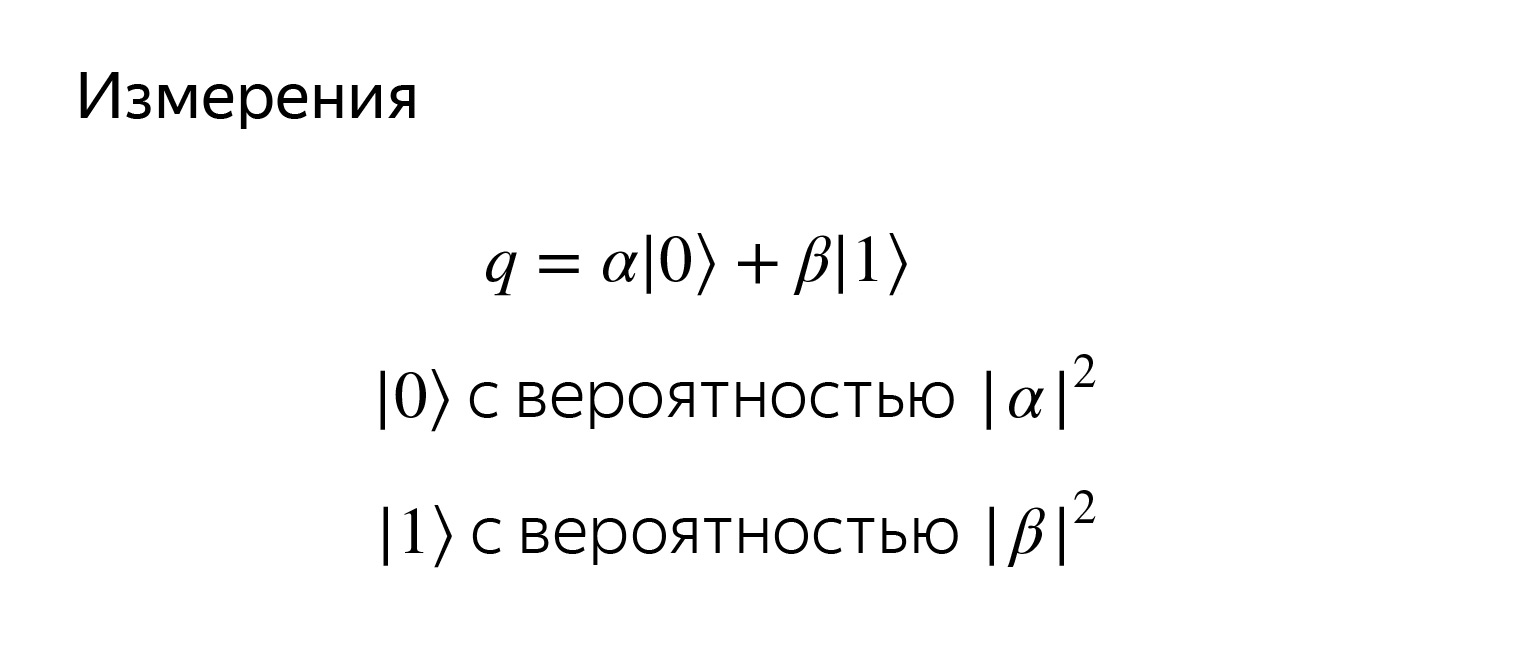
La première chose que nous faisions était d'essayer de calculer la valeur de notre variable, par exemple en Python. Nous voulons lire dans quel état se trouve le qubit. Mais nous ne connaîtrons jamais la signification exacte de α et β.
Si nous essayons de regarder un qubit, de le lire, alors nous obtiendrons un zéro ou un avec les probabilités correspondantes. Les probabilités sont simplement des projections sur les vecteurs de base correspondants.
La deuxième chose que nous pouvons faire est, par exemple, de cloner un qubit. Nous appelons cela l'affectation d'une variable à une autre. Malheureusement, cela ne peut pas être fait dans le monde quantique.

Il n'y a pas d'opération d'affectation, et cela est très lié à ce que je viens de dire: nous ne pourrons même pas regarder la valeur exacte. C'est un résultat fondamental. Il est prouvé très simplement : littéralement deux lignes de comparaisons, par contradiction.
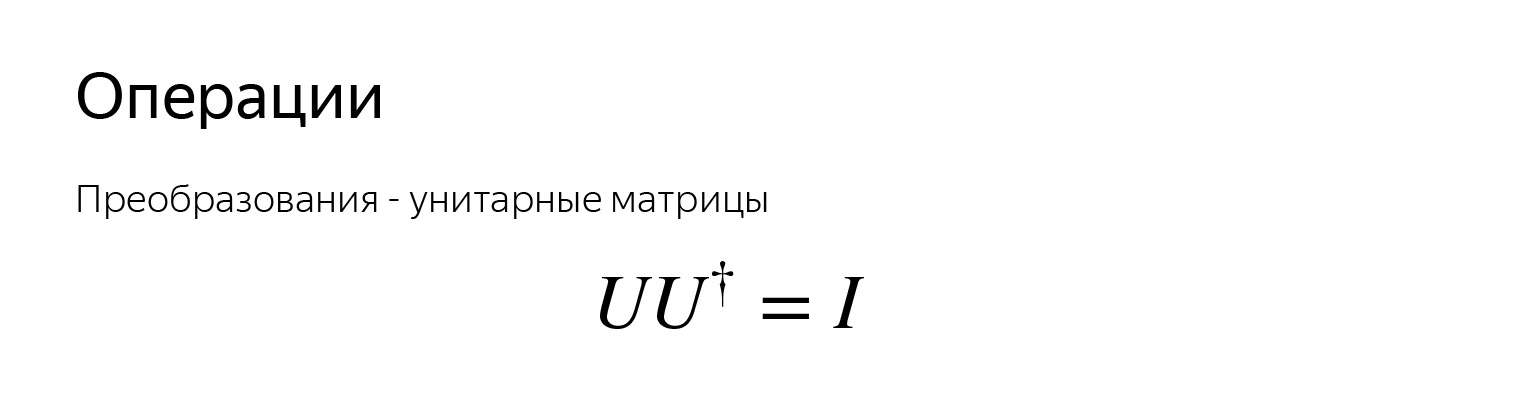
Il y a un qubit que nous ne pouvons pas lire, nous ne pouvons pas cloner. Que pouvez-vous faire du tout?
Un qubit est un vecteur. Le vecteur peut être pris et tourné autour de la sphère. Pour faire pivoter, vous pouvez penser à une matrice qui effectue cette rotation. Toutes les opérations sur les qubits sont des matrices. Ils sont appelés unitaires.
Unitaire - pour qu'une telle condition soit remplie, elle est écrite ici d'une manière astucieuse. Cette icône désigne une matrice conjuguée transposée et complexe. Cette propriété est très importante, cela signifie qu'il y a un inverse pour toute opération. Autrement dit, quelle que soit la façon dont nous déformons le vecteur, nous pouvons toujours le ramener à sa position précédente. Il y a toujours une opération inverse.
Voyons ce que peuvent être les opérations. Ce à quoi nous sommes habitués dans le cas classique. Il y a un zéro, vous pouvez le transformer en un et vice versa.
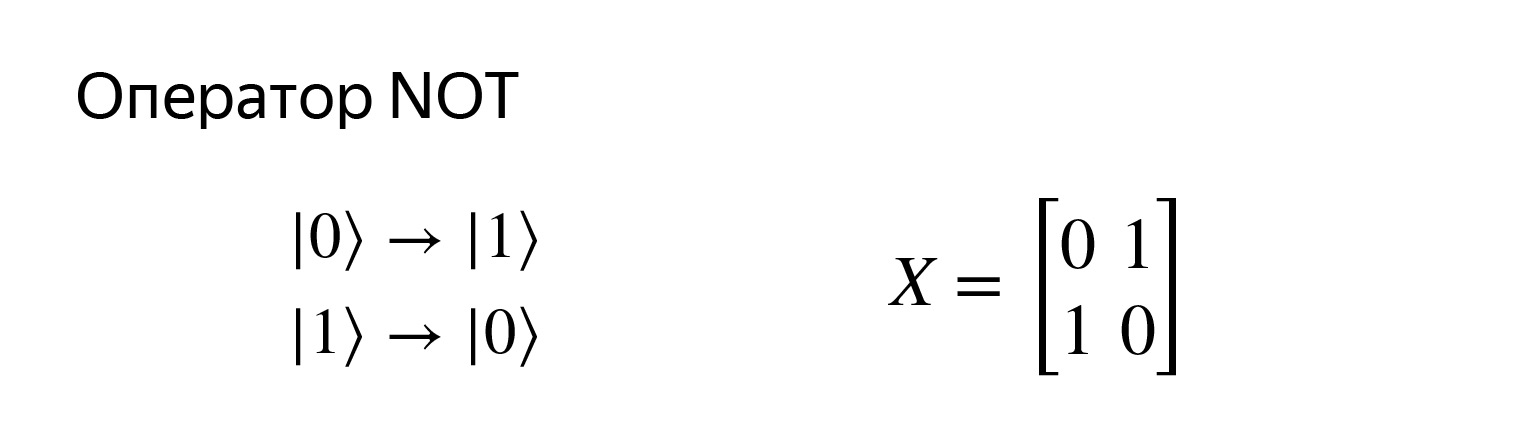
Ceci est l'opérateur de négation et est très simple. Il est enregistré avec une telle matrice. Si nous essayons de nous multiplier, nous obtenons exactement ce que nous voulons.
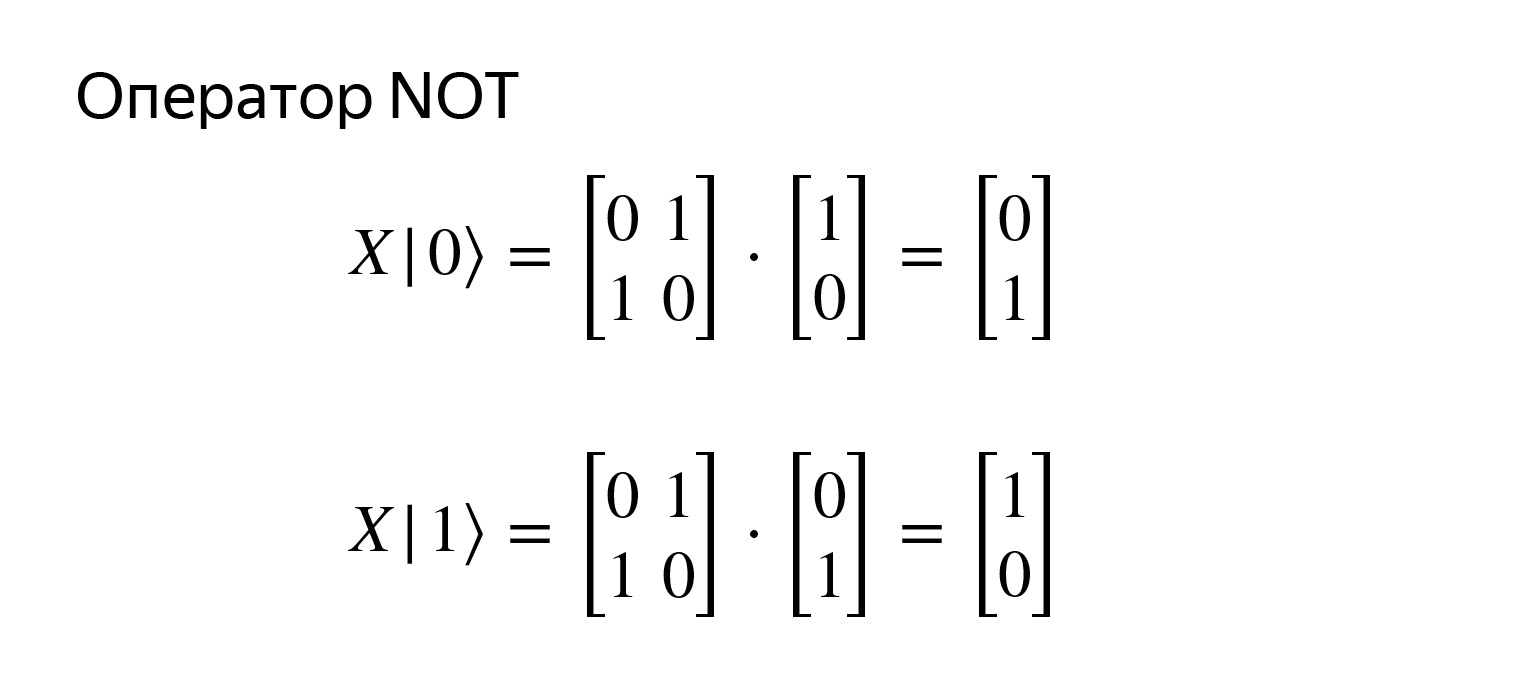
Je l'ai même dessiné ici. Rien de compliqué. L'opérateur de négation a une notation standard, l'opérateur X. À bien y penser, c'est juste une rotation autour d'un des axes. Et il y a les opérateurs Y et Z, la rotation autour d'autres axes, mais ce n'est pas si important maintenant.
Et nous pouvons déjà exécuter notre premier programme sur un ordinateur quantique qui annulera un qubit.
Mais nous, en informatique quantique, bien sûr, écrivons très rarement en Python. Nous utilisons plus souvent des schémas.

Le diagramme ressemble généralement à ceci. Les lignes horizontales sont simplement des valeurs de qubit. J'en ai cinq dessinés ici. Et dans le bloc - l'opération que nous allons faire.
Premier bloc. Un appareil de mesure est dessiné ici. Cela signifie que nous voulons simplement mesurer ce qui est dans le premier qubit.
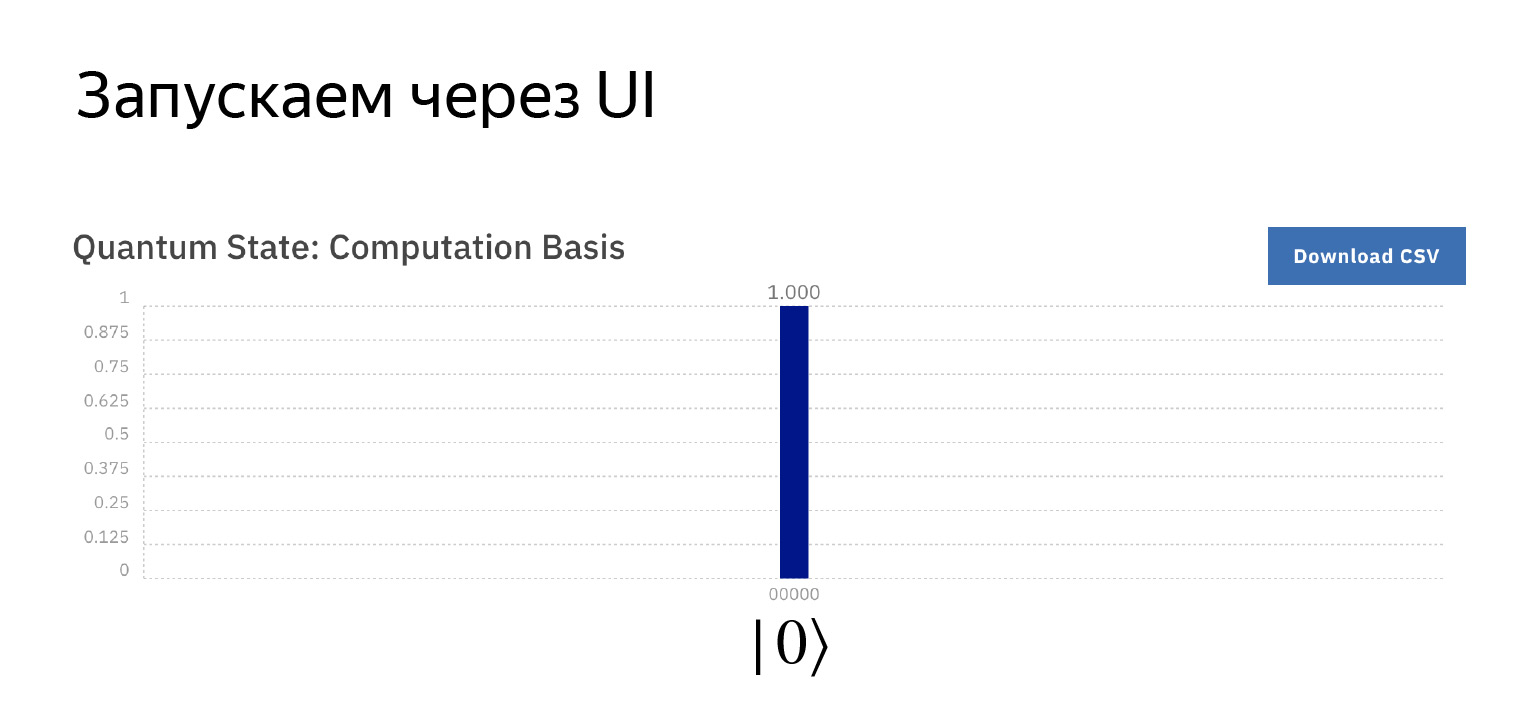
Si nous exécutons cette chose, nous obtenons qu'avec une probabilité de un, nous avons un zéro là-bas, car ils sont initialisés dans cet état et nous n'avons rien fait d'autre avec eux.
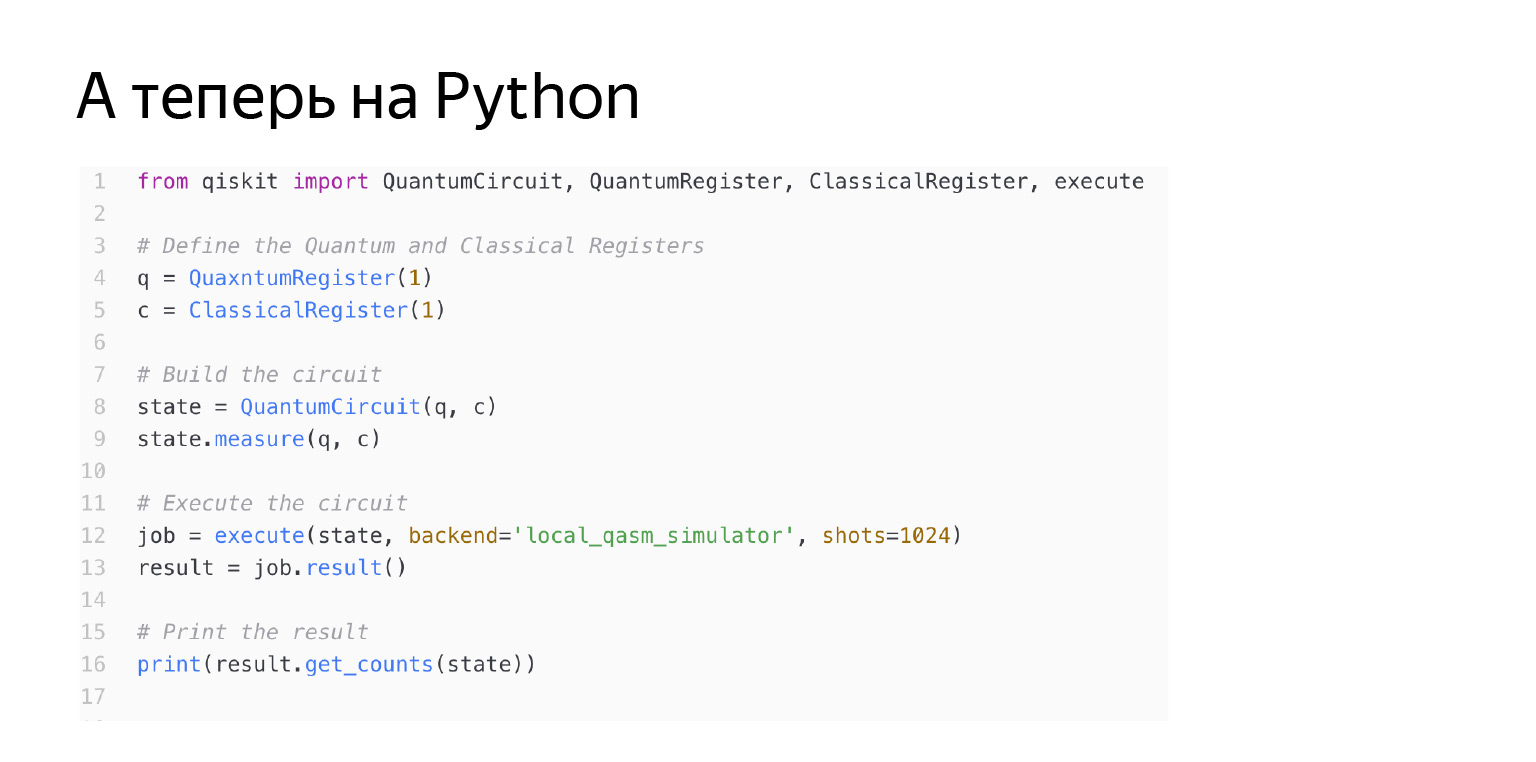
Une telle chose peut être écrite en Python en utilisant la bibliothèque qiskit. Voyons ce qui se passe ici ligne par ligne. Tout d'abord, nous commençons le registre quantique. Je l'allume ici à partir d'un qubit. Et le registre classique. Le registre classique est nécessaire pour écrire le résultat de la mesure quelque part. Autrement dit, je fais des transformations avec un registre quantique, le résultat est un classique un - zéro ou un. Et puis je crée mon propre circuit, qui a ce qubit classique quantique. Je dis juste: mesurons le qubit q en C. Commençons tout cela et tout ira bien. Mais le lecteur attentif verra: il est dit ici que mon backend est un émulateur local.

La même chose peut être faite avec IBM Q, mais il y a un peu plus de code ici. Il y a toutes sortes de nouilles sur le choix d'un appareil qui nous répondra dans les plus brefs délais, en transférant des jetons, c'est tout. Mais il n'y a rien de compliqué.

La même chose peut être faite avec l'opérateur de négation. C'est l'opérateur X, comme je l'ai dit. Cela a exactement la même apparence sur le diagramme, exécutons la même chose.
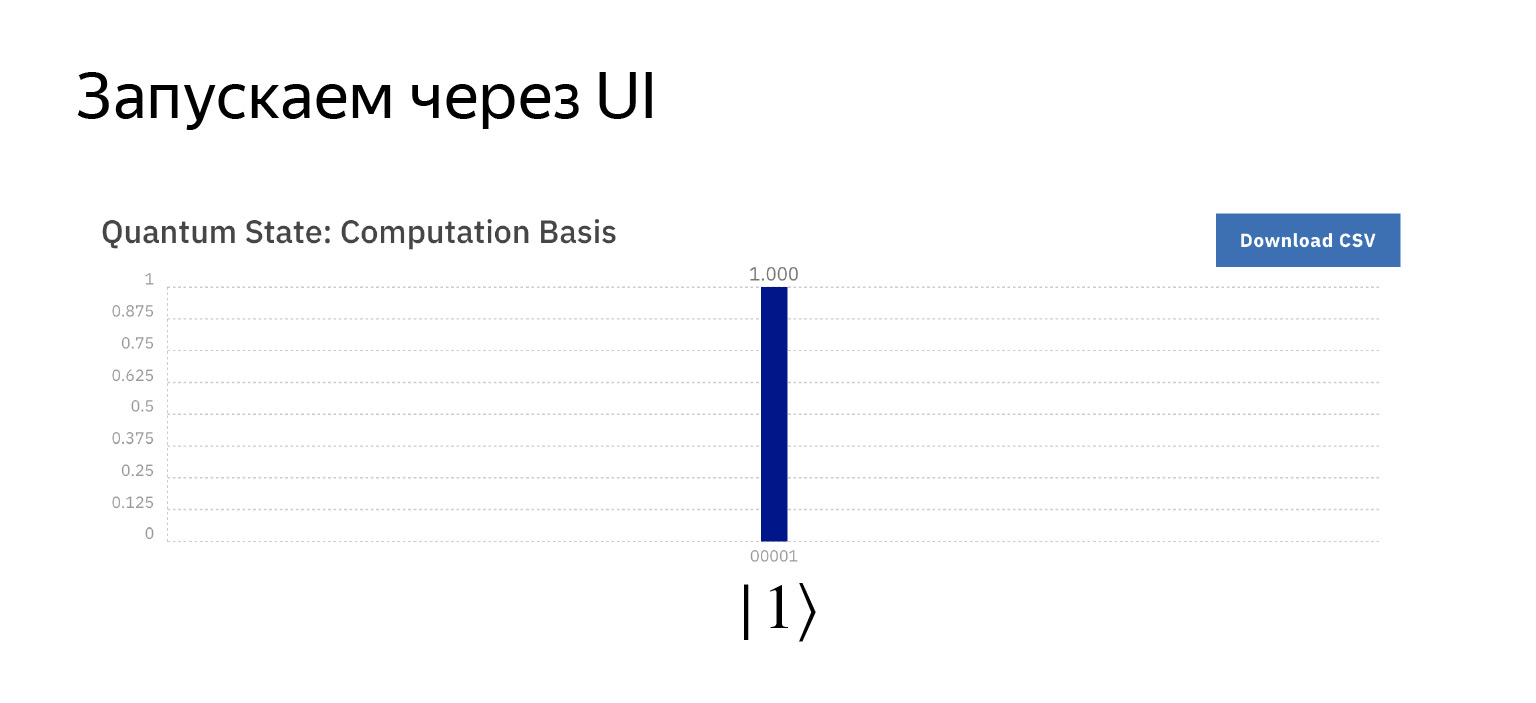
Maintenant, avec une probabilité de un, nous en obtenons une, comme prévu. Pas de magie.
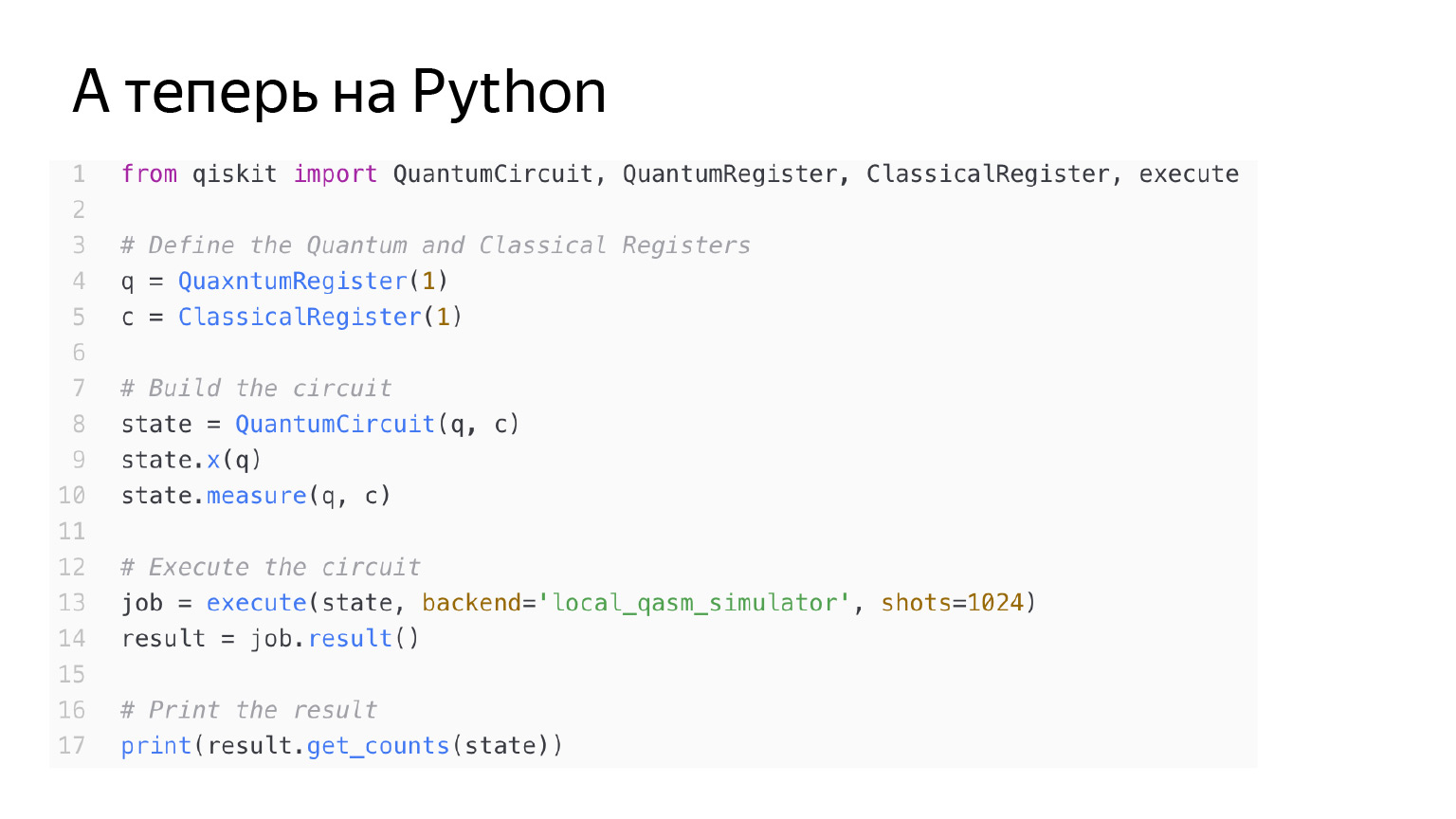
Le code est le même. C'est juste qu'ici j'applique également l'opérateur X au qubit q.
D'accord, essayons d'aller plus loin.
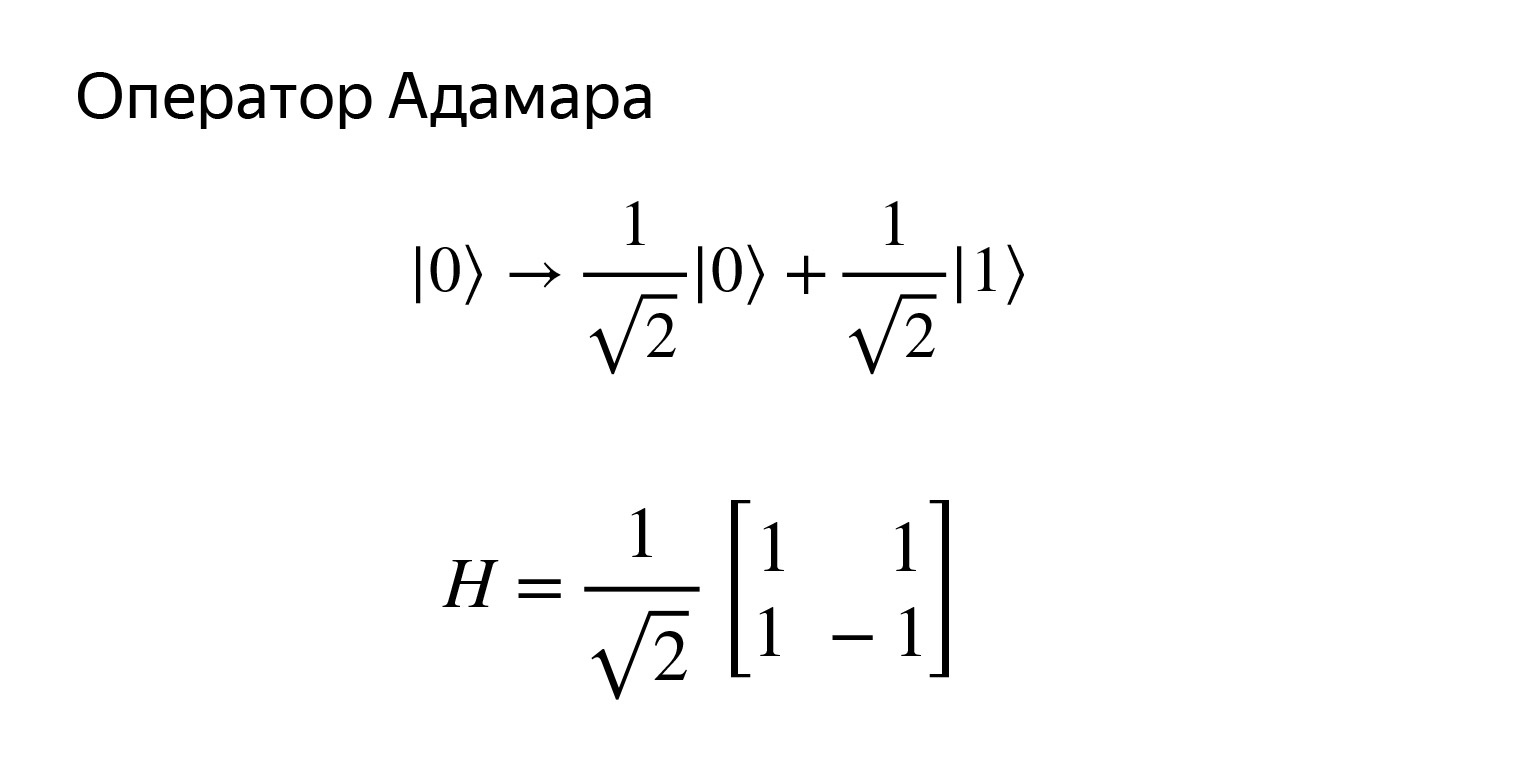
Il y a une chose très délicate ici. Essayons d'obtenir cet état. Cet état est très intéressant. Nous obtiendrons une telle superposition. Si nous essayons de le mesurer, alors avec une probabilité de 1/2, nous obtenons zéro ou un. Autrement dit, ce sera une superposition uniforme, nous pouvons tout obtenir.
Une analogie peut être établie avec ce qu'est un tirage au sort quantique. Nous dirons bien, avec une probabilité ½, nous obtenons zéro et un. La matrice ressemble à ceci.
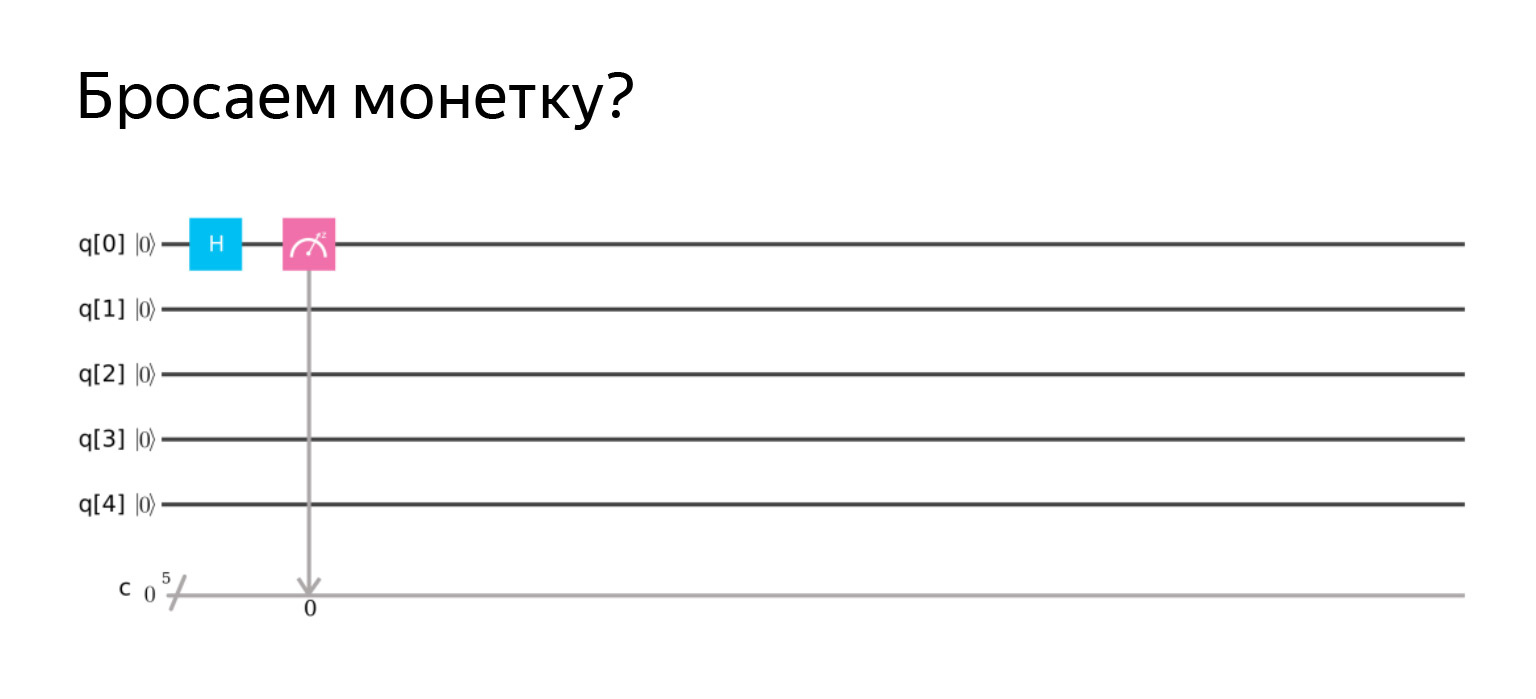
Facile à vérifier, mais nous ne le ferons certainement pas. Dessinons un diagramme. Opérateur H en l'honneur d'Hadamard.
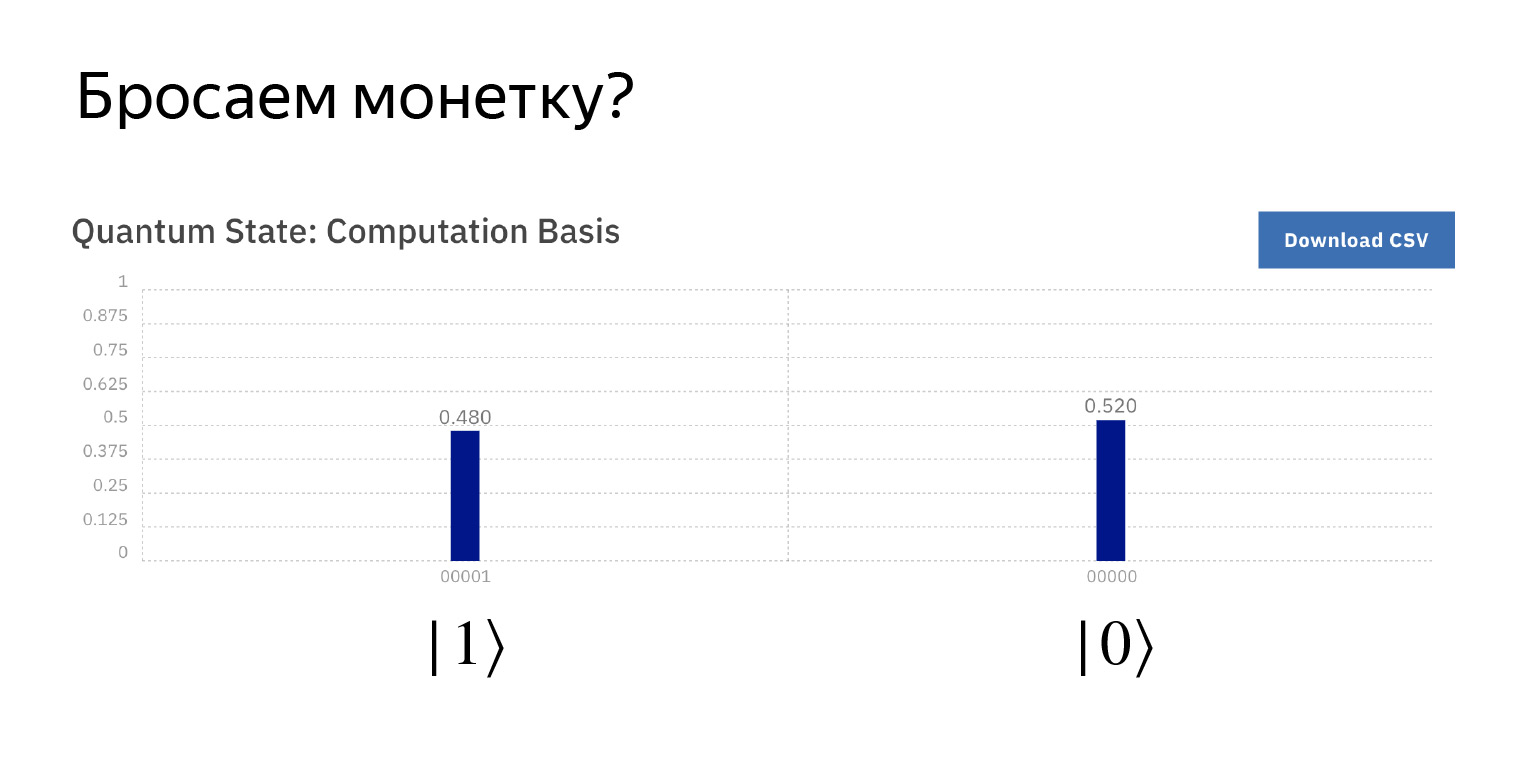
Mesurons et obtenons approximativement ce que nous attendons. Avec une probabilité de ½, zéro et un. Un peu plus, un peu moins, mais c'est comme ça que ça marche.
Voici le code Python, juste pour être là, nous sommes à une conférence Python.

Il y a une telle superposition. Nous lui appliquons l'opérateur Hadamard et mesurons.
Mais vous pouvez lancer une pièce deux fois, nous sommes tous habitués à cela. Si vous lancez une pièce deux fois, rien ne change. Essayons de faire cela dans le cas quantique.

Nous appliquons l'opérateur Hadamard deux fois de suite et nous obtenons toujours un zéro.

Autrement dit, si vous lancez deux fois une pièce quantique, vous obtiendrez toujours un zéro, car l'opérateur Hadamard est inverse de lui-même. Si vous multipliez par vous-même, vous en obtenez toujours un. Voici une chose.
Ainsi, vous pouvez faire quelque chose avec un qubit. Peut être tordu, tordu et mesuré. Essayons d'ajouter plus de qubits. Que faisons-nous dans le monde classique? Prenez et effectuez des opérations logiques simples, "ou" et "et".

Dans le monde quantique, vous ne pouvez pas faire cela, car ils ne sont pas complètement réversibles. Autrement dit, en obtenant zéro dans l'opération «et», nous ne pouvons jamais savoir quelles étaient les valeurs initiales.
Et dans le monde quantique, comme je l'ai dit, une opération est une matrice unitaire toujours réversible. Comment, alors, programmez-vous? Tout ce à quoi nous sommes habitués s'effrite. Mais un nouveau héros apparaît, c'est l'opérateur de la soi-disant négation contrôlée.

Si nous écrivions en Python, cela ressemblerait à ceci. Si le premier qubit est un, inversons le deuxième qubit. Ce n'est pas une matrice, c'est à quoi ressemble l'opérateur. Mais en principe, ce que j'ai dit est écrit ici. Là où il y a une unité dans le premier qubit, le second est inversé.
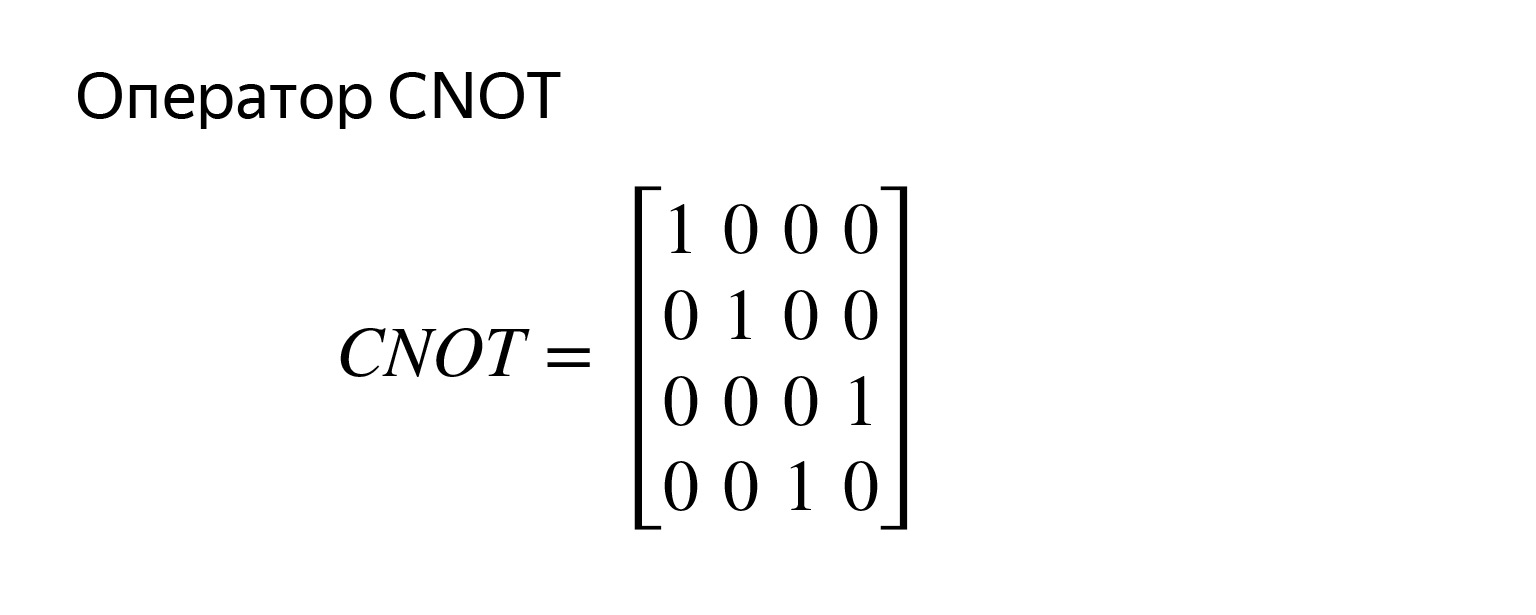
La matrice est déjà quatre par quatre. Pour deux qubits, cela ressemble à ceci. Je laisse le problème avec un astérisque pour se multiplier et voir si c'est vrai.

Cette chose peut même être programmée. Pas de science de fusée. Il suffit de prendre, de créer un circuit avec deux qubits, avec deux classiques, et de faire, non seulement CNOT, mais CX, une négation contrôlée.
La négation était l'opérateur X, donc en principe tout est logique. Et vous pouvez dessiner un diagramme. Le schéma est le suivant.
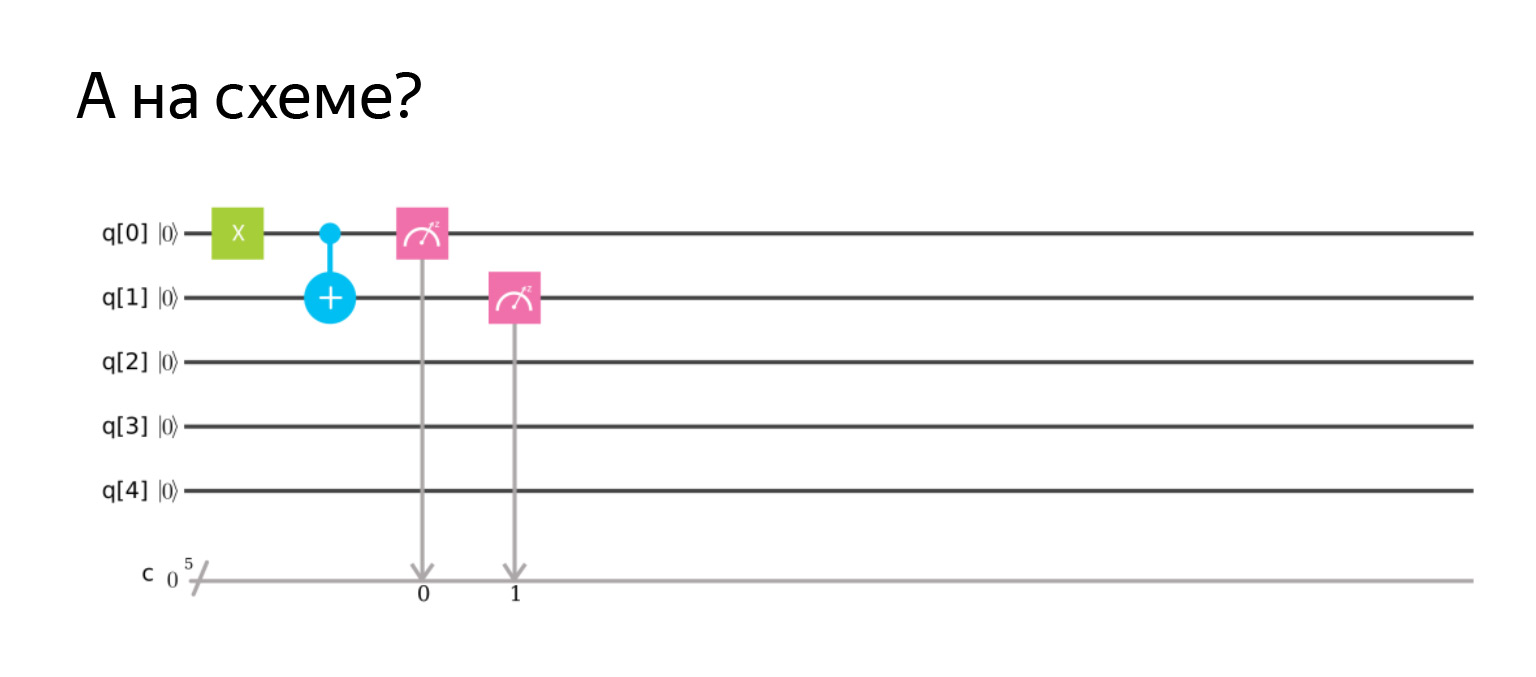
Autrement dit, la négation contrôlée est un tel plus sur le qubit que nous voulons changer. Et le point, qui est le contrôle. Ici, si le qubit est dans l'unité, alors nous changerons le second.

Ici, j'inverse d'abord spécifiquement le premier pour qu'il en soit un, puis je mesure les deux et j'obtiens le résultat | 11⟩. Tout est comme prévu.
Mais le moment est venu d'utiliser toutes nos connaissances ensemble.

Prenons les trois ou quatre opérateurs que nous connaissons et regroupons-les dans un seul schéma. Autrement dit, nous appliquons l'opérateur Hadamard au premier opérateur. Inversez le second, puis tous ensemble, effectuez une négation et une mesure contrôlées.
Ne l'exécutons pas encore, mais essayons de deviner ce qui va se passer.
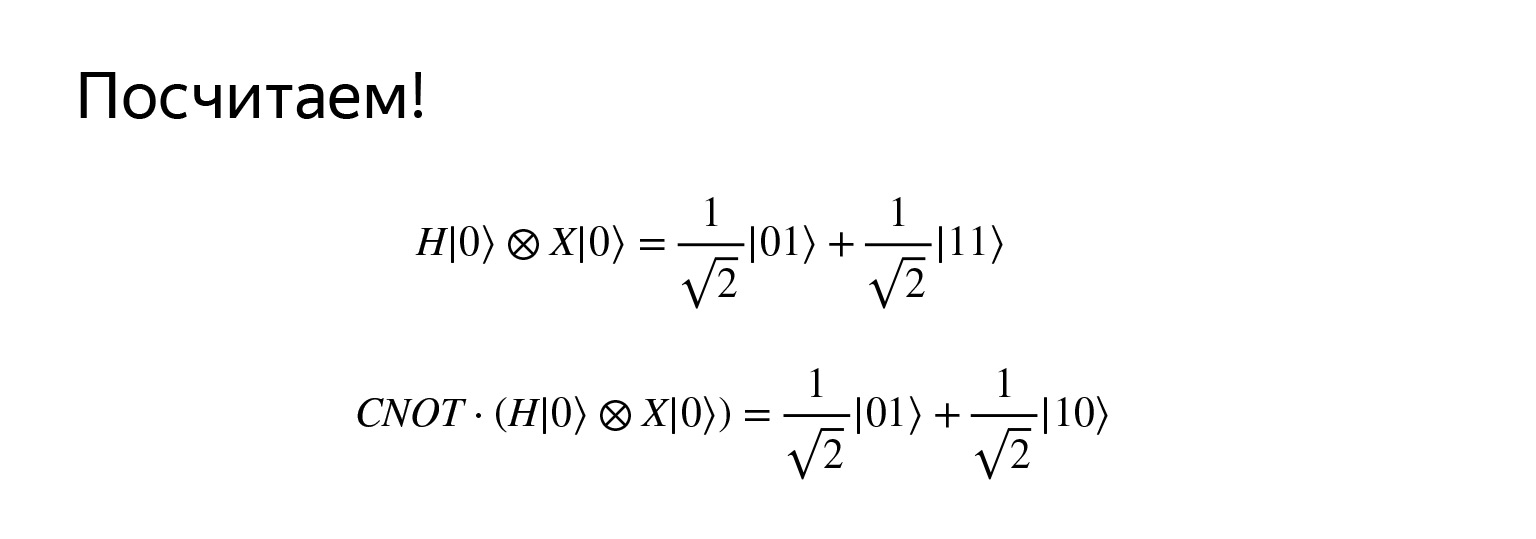
Si nous appliquons l'opérateur Hadamard au premier qubit et annulons le second, alors nous obtenons une telle superposition. Je ne veux pas perdre de temps à vérifier maintenant, cela peut être facilement multiplié. Mais la position est très intéressante. Premièrement, il est très similaire à uniforme, et, deuxièmement, maintenant cet état est appelé intriqué, si nous prenons également la négation contrôlée.

L'État est déroutant. Et pourquoi? Essayons de faire une mesure. Regardez, si je mesure le premier qubit et que je l'ai dans l'état zéro, alors je peux dire que le deuxième qubit est nécessairement dans l'état un.
Autrement dit, si je fais une telle transformation avec mes qubits, je donne un qubit à mon ami, il s'envolera pour New York, et je mesure le deuxième qubit moi-même, je saurai exactement dans quel état se trouve son qubit. C'est ce qu'on appelle l'effet de l'intrication quantique ou de la connectivité quantique. Et c'est le principal mécanisme par lequel fonctionne l'informatique quantique. Cela va changer, ils sont très rigidement connectés, et pendant la mesure on ne peut obtenir que | 00⟩ ou | 11⟩.
A cette occasion, il y a une illustration très intéressante en faveur d'un scientifique, autrichien, à mon avis,

La distraction était qu'il portait des chaussettes différentes tout le temps. Et ses collègues ont plaisanté à son sujet: s'il entre dans la pièce avec un pied et qu'on voit que la chaussette est rose, alors on peut définitivement dire que la deuxième chaussette n'est pas rose. Alors ça va.
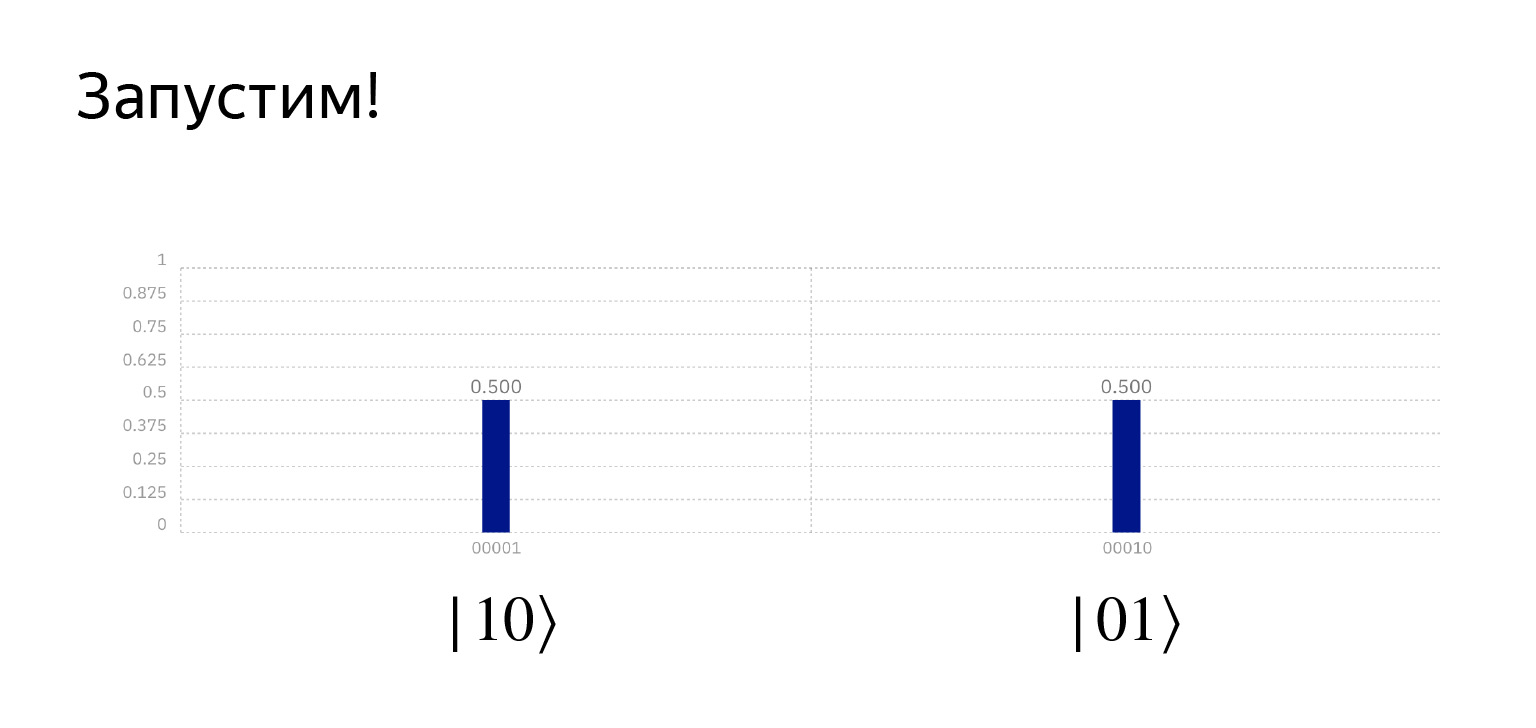
Si nous exécutons cette chose, nous obtenons exactement ce que nous voulons. C'est déjà assez drôle ici. La probabilité est exactement de 0,5, mais c'est une coïncidence.
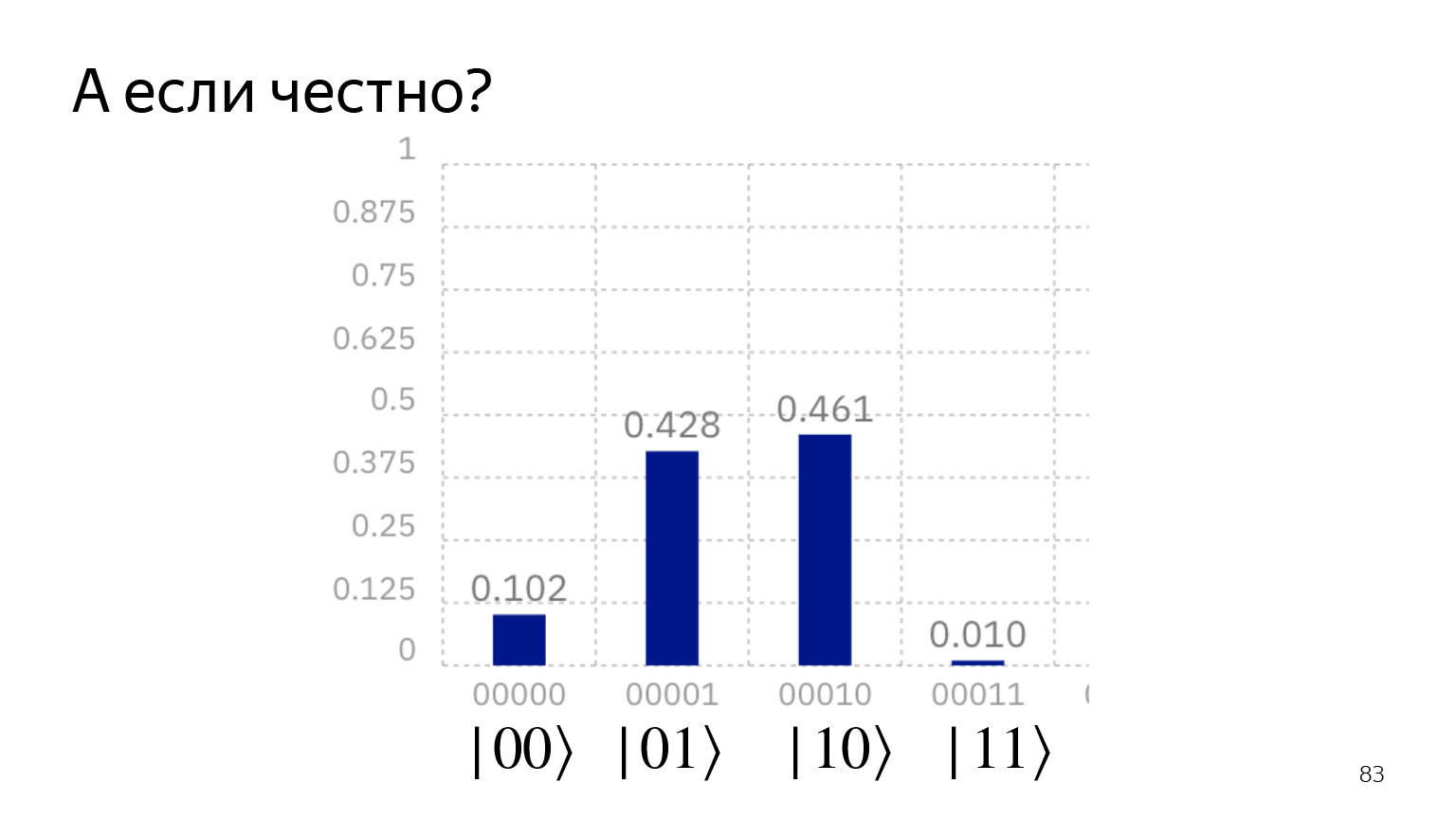
Si nous exécutons honnêtement sur un ordinateur quantique, nous obtenons cette image. Nous semblons dire: l'état | 00⟩ ne peut jamais être obtenu et l'état | 11⟩ ne peut jamais être obtenu. Mais cela fonctionne toujours: l'état actuel de la technologie est tel qu'il y a des bruits qui ne peuvent pas toujours être facilement supprimés. Et ils ont du mal avec ça.
Mais si vous vous souvenez de l'informatique classique, c'est la même chose: des codes correcteurs d'erreurs et tout ça. C'est juste que le qubit est trop petit pour l'instant pour dépenser des bits supplémentaires en correction d'erreur.
Maintenant, comme je l'ai promis, quelques exemples d'algorithmes. Mais ce ne seront que des exemples infondés sans analyse d'algorithmes, de sorte que vous regardez, réfléchissez, devenez intéressé.

Le premier algorithme est juste lié à Deutsch, dont nous avons parlé au début. C'est l'algorithme Deutsch-Jozy. Et il fait ce qui suit. Imaginons que nous ayons une fonction booléenne en n variables. Et nous savons avec certitude qu'elle est constante ou équilibrée. Équilibré signifie que sur exactement la moitié des arguments, il est égal à zéro et sur l'autre moitié à un. Essayons de vérifier classiquement si elle est constante ou non.
Pour ce faire, nous devons cocher au moins la moitié de toutes les options possibles: 2 n - 1 +1 option. L'algorithme quantique vous permet de faire cela en n appels à la fonction elle-même, en n calculs de la fonction elle-même. Il s'agit d'un nombre de hits exponentiellement inférieur.
Le deuxième exemple est probablement bien connu de tous, à cause de lui on dit que les ordinateurs quantiques vont casser toute cryptographie: on peut factoriser les nombres quantiques très rapidement.

Des estimations de difficulté sont données ici et il y a un exemple fantastique. En 2011, le nombre 15 a été factorisé sur un vrai ordinateur, il fallait sept qubits.

Mais tout n'est pas si mauvais. Dans le cas où les ordinateurs quantiques atteignent le niveau auquel vous pouvez casser RSA, il existe déjà une cryptographie post-quantique. Il repose sur l'apprentissage avec des erreurs. C'est à ce moment qu'une petite erreur est introduite dans le problème de sorte qu'il est très difficile de trouver une réponse. Ce sont généralement des équations ou un système d'équations. Voici un exemple de l'algorithme. Quiconque le souhaite peut lire plus en détail.
Le plus intéressant: l'algorithme New Hope est basé sur cette chose , le nouvel espoir de toute l'humanité. En 2016, Chrome a ajouté la prise en charge de cet algorithme. Il y a un lien vers le blog ici. Ce n'était pas mon idée, tout l'est vraiment. L'avenir est déjà là.
Il y a quelques liens à la fin:
- , : Michael A.Nielsen and Isaac L. Chuang, «Quantum Computation and Quantum Information». , . .
- IBM Q: quantumexperience.ng.bluemix.net
- IBM Q User Guide: quantumexperience.ng.bluemix.net/proxy/tutorial/full-user-guide/introduction.html
- Qiskit: qiskit.org
- :
nplus1.ru/material/2017/06/07/quantumcomputers
nplus1.ru/news/2017/05/26/quantum-blockchain
C'est plus ou moins tout. Je veux juste ajouter qu'il y a environ 50 ans, lorsque Deutsch a commencé à faire de la science de l'information quantique, les ordinateurs étaient gros. Ils ont été fabriqués par plusieurs entreprises. Ils avaient à peu près la taille d'une armoire. Et maintenant, à peu près les mêmes entreprises fabriquent de gros ordinateurs quantiques. Et, bien sûr, nous ne savons pas ce qui se passera dans 50 ans.
Si vous essayez de taper votre moteur de recherche préféré, vous pouvez aujourd'hui trouver des postes vacants pour un programmeur quantique. Bien sûr, il y a plus de recherche là-bas, mais néanmoins. Remercier.