Bonjour chers collègues! Je n'ai pas écrit sur Habr depuis cent ans, mais maintenant le moment est venu. Ce printemps, j'ai enseigné le cours Advanced ML à la MADE Big Data Academy de Mail.ru Group; Il semble que les auditeurs aient aimé, et maintenant on m'a demandé d'écrire moins un message publicitaire qu'un article éducatif sur l'un des sujets de mon cours. Le choix était proche de l'évidence: à titre d'exemple de modèle probabiliste complexe, nous avons discuté d'un modèle SIR épidémiologique extrêmement pertinent (apparemment ... mais plus à ce sujet plus tard) qui modélise la propagation des maladies dans une population. Il a tout: une inférence approximative via les méthodes Markov Monte Carlo, et des modèles Markov cachés avec l'algorithme stochastique de Viterbi, et même des données de présence uniquement.



Avec ce sujet, une seule petite difficulté est apparue: j'ai commencé à écrire sur ce que j'ai réellement dit et montré lors de la conférence ... et d'une manière ou d'une autre rapidement et imperceptiblement vingt pages de texte (enfin, avec des images et du code) accumulées, ce qui n'est toujours pas était terminé et n'était pas du tout autonome. Et si vous dites tout de manière à ce que tout soit clair à partir de «zéro» (pas de zéro absolu, bien sûr), alors vous pourriez écrire une centaine de pages. Donc un jour je les écrirai certainement, mais maintenant je présente à votre attention la première partie de la description du modèle SIR, dans laquelle nous ne pouvons que poser un problème et décrire le modèle de son côté générateur - et si le public respecté a un intérêt, alors ce sera possible procéder.

Modèle SIR: énoncé du problème

J'aime mes amis et ils m'aiment,

nous sommes aussi proches que possible.

Et juste parce que nous nous soucions vraiment de

tout ce que nous obtenons, nous le partageons!



Tom Lehrer. Je l'ai eu d'Agnès

Alors découvrons-le. De manière informelle, les hypothèses de base du modèle SIR sont les suivantes:

• il y a une certaine population de personnes dans laquelle un virus terrible peut marcher;
• initialement, le virus pénètre dans la population d'une manière ou d'une autre (par exemple, la première personne malade apparaît), puis les gens sont infectés les uns par les autres;
• SIR , :
  
     ○ Susceptible ( , , .. ),
  
     ○ Infected ( )
  
     ○ Recovered ().

Pour simplifier, nous supposerons que ceux qui ont été malades développent toujours une immunité et sont exclus du cycle du virus dans la nature. Par conséquent, les transitions entre ces états ne peuvent se faire que de gauche à droite: Susceptible → Infecté → Récupéré.



La tâche est, en fait, d'entraîner ce modèle, c'est-à-dire de comprendre quelque chose sur les paramètres du processus d'infection à partir des données. Il est facile de comprendre à quoi ressemblent les données - il s'agit simplement du nombre d'infectés enregistrés à chaque instant dans le temps, que nous désignerons par le vecteur$$$\boldsymbol{y}$... Par exemple, lorsque j'ai donné mes devoirs dans le cours sur le coronavirus (il s'agissait cependant d'autres modèles), les données pour la Russie ressemblaient à ceci:

[2,2,2,2,3,4,6,8,10,10,10,10,15,20,25,30,45,59,63,93,114,147,199,253,306,438,438,495,658,840,1036,1264,1534,1836,2337,2777,3548,4149,4731,5389,6343,7497,8672]

Mais quels sont les paramètres de ce modèle, comment ils s'interfacent les uns avec les autres et comment les former, en particulier sur un si petit ensemble de données, est une question plus sérieuse.



De manière générale, je suivrai les grandes lignes du travail ( Fintzi et al., 2016 ), qui construit des algorithmes MCMC pour les modèles SIR, SEIR et certaines de leurs variantes. Mais en comparaison avec ( Fintzi et al., 2016 ), je vais grandement simplifier à la fois le modèle et sa présentation. La principale simplification est qu'au lieu du temps continu, qui est considéré dans l'œuvre originale, nous considérerons le temps discret, c'est-à-dire au lieu d'un processus continu qui à un moment donné génère des événements de la forme "infecté" et "récupéré", nous considérerons que les gens traversent un ensemble de points discrets dans le temps$$$t=1,\ldots,T$... Cette simplification va nous permettre, d'une part, de s'affranchir de nombreuses difficultés techniques, et d'autre part, de passer de l'algorithme Metropolis-Hastings en général à l'algorithme d'échantillonnage de Gibbs, c'est-à-dire de ne pas calculer le ratio Metropolis, comme il faut le faire dans ( Fintzi et al., 2016 ). Si vous ne comprenez pas ce que je viens de dire, ne vous inquiétez pas: nous n'en aurons pas besoin aujourd'hui, et s'il y a des parties suivantes, je vais tout vous expliquer.



Nous désignerons les états du modèle SIR par S, I et R, respectivement, et l'état d'une personne$$$i$ en ce moment $$$t$ - à travers $$$x_i^{(t)}\in\{S, I, R\}$... Dans le même temps, nous introduirons immédiatement des variables pour le nombre total de patients qui ne sont pas encore tombés malades.$$$S^{(t)}$malade $$$I^{(t)}$ et récupéré $$$R^{(t)}$ en ce moment $$$t$... L'homme total que nous aurons$$$N$donc pour n'importe qui $$$t$ sera exécuté $$$S^{(t)} + I^{(t)} + R^{(t)} = N$... Et, comme je l'ai écrit ci-dessus,$$$y^{(t)}$parmi eux sont des malades enregistrés (testés).



Les paramètres inconnus du modèle sont$$$\boldsymbol\theta = \{\beta, \mu, \rho, \boldsymbol{\pi}\}$où:

• $$$\boldsymbol\pi$ - la distribution initiale des cas; en d'autres termes,$$$x^{(1)}_j\sim \boldsymbol{\pi}$ pour chaque $$$j$; dans notre modèle simplifié, nous ne formerons pas$$$\boldsymbol\pi$, mais nous enregistrerons simplement 1 à 2 cas au premier moment;
• $$$\rho$ - la probabilité de trouver une personne infectée dans la population générale, c'est-à-dire la probabilité qu'une personne $$$x_j$ sur le moment $$$t$quand $$$x_j^{(t)}=I$, sera détecté par le test et inscrit dans les données $$$y^{(t)}$; en d'autres termes, pour chaque personne malade, nous lançons une pièce pour déterminer si le test le trouvera ou non, donc l'élément actuel est$$$y_t$ a une distribution binomiale avec des paramètres $$$I^{(t)}$ et $$$\rho$:

  $$

  $$y^{(t)}\mid I^{(t)}, \rho \sim \mathrm{Binomial}(I^{(t)}, \rho);$$

• $$$\mu$ - la probabilité qu'une personne malade se rétablisse en un temps, c'est-à-dire la probabilité de transition d'un état $$$I$ en état $$$R$;

ET $$$\beta$ - C'est le paramètre le plus intéressant montrant la probabilité d'infection en un décompte de temps pour une personne infectée . Cela signifie que dans le modèle, nous supposons que toutes les personnes de la population «communiquent» entre elles («communication» signifie ici un contact suffisant pour la transmission de la maladie; le coronavirus est transmis principalement par des gouttelettes en suspension dans l'air, mais, bien sûr, il est possible de modéliser et la propagation de toute autre maladie; voir, par exemple, l'épigraphe), et la probabilité d'être infecté dépend du nombre actuellement infecté, c'est-à-dire de ce qui est$$$I^{(t)}$... Nous supposerons le modèle le plus simple dans lequel la probabilité d'infection d'une personne infectée est$$$\beta$, et tous ces événements sont indépendants, ce qui signifie que la probabilité de rester en bonne santé est

$$

$$(1-\beta)^{I^{(t)}}.$$

Ces hypothèses ont en fait beaucoup à discuter. La chose la plus surprenante ici, à mon avis, est la distribution binomiale pour$$$y^{(t)}$... Lancer une pièce avec la probabilité de détecter une personne infectée est tout à fait normal, mais il n'est pas très réaliste de relancer cette pièce à chaque étape, c'est-à-dire que nous pouvons «oublier» une personne infectée déjà détectée. En conséquence, le modèle SIR peut (et le fait souvent) produire une séquence complètement non monotone$$$\boldsymbol{y}$; c'est étrange, mais cela ne semble pas avoir beaucoup d'effet sur le résultat, et il serait beaucoup plus difficile de modéliser ce processus de manière plus réaliste.



De plus, il est évident que ce modèle est destiné à une population fermée, où tout le monde «communique» avec tout le monde, il n'a donc aucun sens de le lancer, par exemple, pour la Russie avec le paramètre N de cent millions ou pour Moscou avec le paramètre dix millions (et ne fonctionnera pas). Une direction importante des extensions et extensions des modèles SIR y est consacrée: comment ajouter un graphique plus réaliste des interactions et des infections possibles; nous en parlerons probablement dans le dernier post.



Mais avec toutes ces simplifications, maintenant, en utilisant les paramètres ci-dessus, nous pouvons écrire la matrice de probabilité de la transition entre les états. Ces probabilités (plus précisément, plus précisément la probabilité d'être infecté) dépendent des statistiques générales de la population. Désignons le vecteur des états de toutes les personnes sauf$$$x_j$, à travers $$$\boldsymbol{x}_{-j}$, et étendre la même notation à toutes les autres variables; par exemple,$$$I_{-j}^{(t)}$ Est le nombre d'infectés à la fois $$$t$, sans parler de $$$x_j$... Ensuite, pour les probabilités de transition de$$$x_j^{(t-1)}$ à $$$x_j^{(t)}$ on a

$$

$$p\left(x_j^{(t)}=S\mid x_j^{(t-1)}=S, \boldsymbol{x}_{-j}^{(t-1)}\right) = (1 - \beta)^{I_{-j}^{(t-1)}},$$

$$

$$p\left(x_j^{(t)}=I\mid x_j^{(t-1)}=S, \boldsymbol{x}_{-j}^{(t-1)}\right) = 1 - (1 - \beta)^{I_{-j}^{(t-1)}},$$

$$

$$p\left(x_j^{(t)}=R\mid x_j^{(t-1)}=I, \boldsymbol{x}_{-j}^{(t-1)}\right) = \mu,$$

$$

$$p\left(x_j^{(t)}=I\mid x_j^{(t-1)}=I, \boldsymbol{x}_{-j}^{(t-1)}\right) = 1 - \mu,$$

et dans tous les autres cas

$$

$$p\left(x_j^{(t)}\mid x_j^{(t-1)}, \boldsymbol{x}_{-j}^{(t-1)}\right) = 0.$$

La même chose peut être écrite plus clairement sous la forme d'une matrice de probabilité de transition (l'ordre des lignes et des colonnes est naturel, SIR):

$$

$$\left(\begin{matrix} (1 - \beta)^{I_{-j}^{(t-1)}} & 1 - (1 - \beta)^{I_{-j}^{(t-1)}} & 0 \\ 0 & 1 - \mu & \mu \\ 0 & 0 & 1\end{matrix}\right)$$

Pour un lecteur familiarisé avec les chaînes de Markov et les modèles de Markov, il peut sembler qu'il ne s'agit que d'un modèle de Markov caché: il y a un état caché, il y a une distribution claire des observables pour chaque état caché, les transitions sont vraiment Markov, c'est-à-dire que le prochain état caché ne dépend que du précédent ... Mais il y a , comme on dit, il y a une mise en garde: les probabilités de transition ne peuvent pas être considérées comme constantes, elles changent avec le changement$$$I^{(t)}$et c'est un aspect extrêmement important du modèle qui ne peut être jeté.



Par conséquent, l'inférence dans ce modèle devient soudainement beaucoup plus difficile que dans le modèle de Markov caché habituel (bien qu'il n'y ait pas toujours un tel cadeau). Cependant, bien que la conclusion soit plus compliquée, elle est toujours soumise à l'esprit humain - dans les prochaines installations (le cas échéant), je vous en parlerai. Et pour aujourd'hui, presque assez c'est assez - maintenant, détendons-nous un peu et essayons de jouer avec ce modèle pour l'instant dans un sens génératif.

Exemple de génération de données

En tant que grand connaisseur et expert, un

introverti est entré en quarantaine.

***

«Je ne pouvais pas travailler à la maison»,

tenta d'expliquer l' abeille aux vers.

***

Kaganov est mort en plaisantant joyeusement.

Bien sûr, je suis vraiment désolé pour lui, cependant ...



Leonid Kaganov. Quarantaines

Si les paramètres du modèle sont connus et qu'il suffit de générer une trajectoire de l'évolution de la propagation de la maladie dans la population, il n'y a rien de compliqué dans le SIR. Le code ci-dessous génère un exemple de population selon notre modèle; états que j'ai codés comme$$$S=0$, $$$I=1$, $$$R=2$... Comme je l'ai averti, pour simplifier, je suppose que pour le moment$$$t=0$ il y a exactement une personne malade dans la population, et puis ça continue.

def sample_population(N, T, true_rho, true_beta, true_mu):
    true_log1mbeta = np.log(1 - true_beta)

    cur_states = np.zeros(N)
    cur_states[:1] = 1
    cur_I, test_y, true_statistics = 1, [1], [[N-1, 1, 0]]

    for t in range(T):
        logprob_stay_healthy = cur_I * true_log1mbeta
        for i in range(N):
            if cur_states[i] == 0 and np.random.rand() < -np.expm1(logprob_stay_healthy):
                cur_states[i] = 1
            elif cur_states[i] == 1 and np.random.rand() < true_mu:
                cur_states[i] = 2

        cur_I = np.sum(cur_states == 1)
        test_y.append( np.random.binomial( cur_I, true_rho ) )
        true_statistics.append([np.sum(cur_states == 0), np.sum(cur_states == 1), np.sum(cur_states == 2)])

    return test_y, np.array(true_statistics).T

N, T, true_rho, true_beta, true_mu = 100, 20, 0.1, 0.05, 0.1
test_y, true_statistics = sample_population(N, T, true_rho, true_beta, true_mu)

Ce code ne donne pas seulement les données réelles $$$\boldsymbol{y}$mais aussi de "vraies" statistiques $$$S^{(t)}$, $$$I^{(t)}$, $$$R^{(t)}$afin qu'ils puissent être visualisés. Faisons le; pour les paramètres$$$N=100$, $$$T=20$, $$$\rho=0.1$, $$$\beta=0.2$, $$$\mu=0.3$vous pouvez obtenir quelque chose comme ceci:







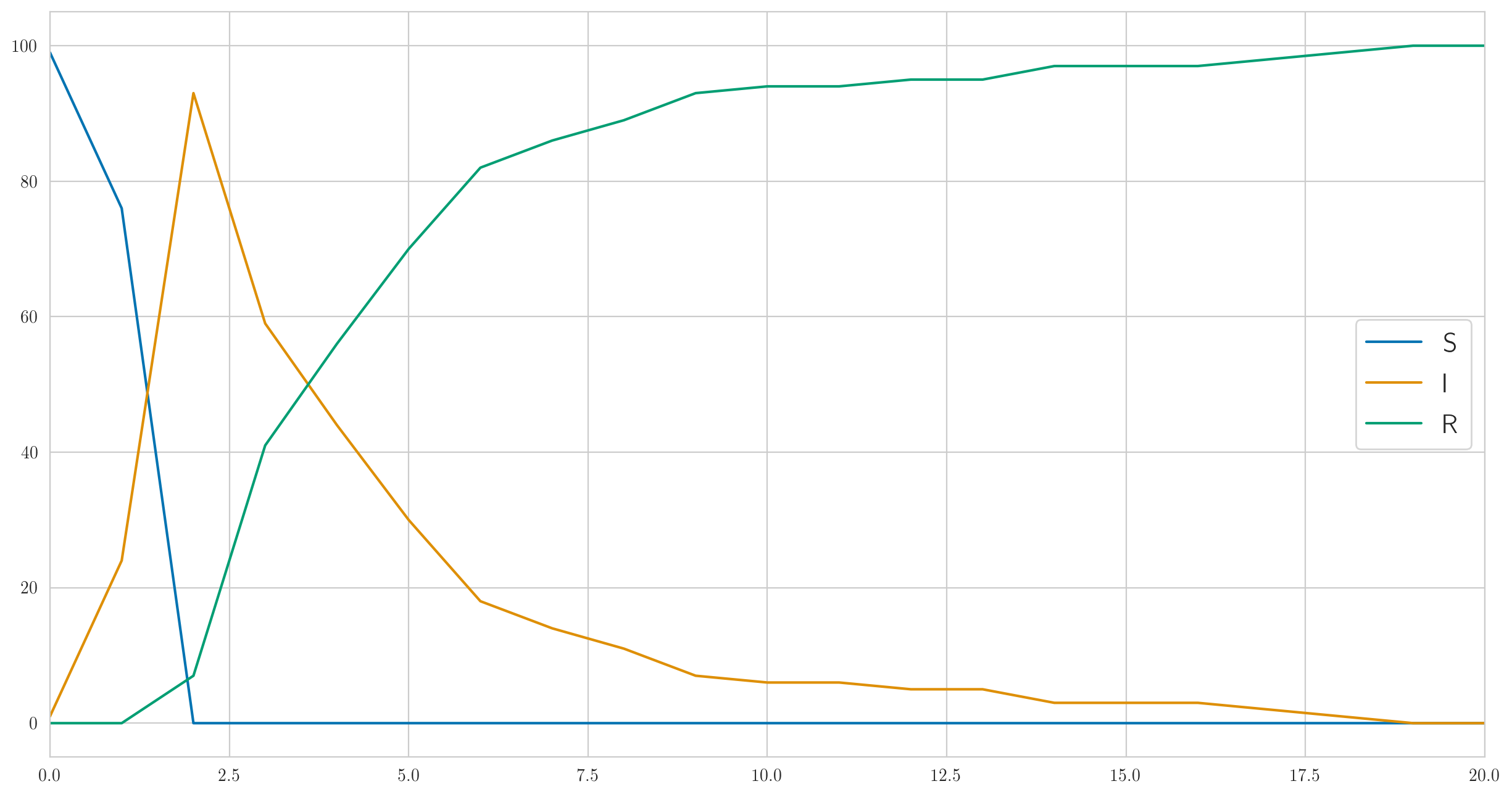
comme vous pouvez le voir, dans cet exemple, tout le monde tombe malade très rapidement, puis commence lentement à aller mieux. Et les données réelles observées sur les malades ressemblent à ceci:

[1 6 13 6 6 4 1 0 0 1 0 1 2 0 0 0 0 0 1 0 0]

Notez que, comme nous l'avons vu ci-dessus, il n'y a pas de monotonie ici.



Mais ce n'est certainement pas le seul comportement possible. J'ai choisi les paramètres ci-dessus pour que l'infection soit suffisamment rapide et que la maladie couvre presque immédiatement les cent personnes de notre population testée. Et si tu fais$$$\beta$ plus petit, par exemple $$$\beta=0.01$, alors l'infection ira beaucoup plus lentement, et même tout le monde n'aura pas le temps de tomber malade avant que le dernier malade ne guérisse et ne restera pas. Quelque chose comme ceci:







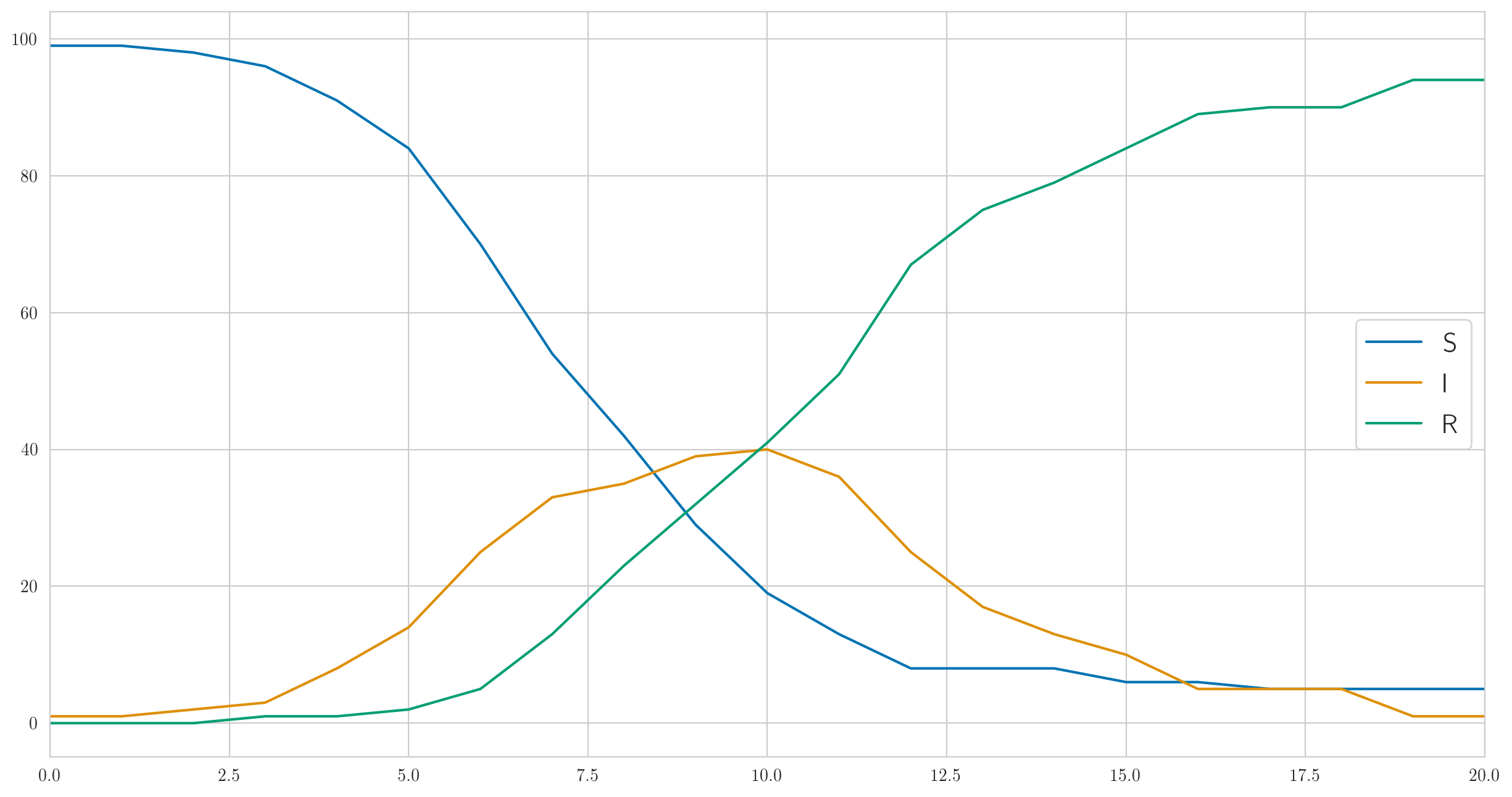
Et le nombre de cas détectés est également complètement différent:

[1 0 0 0 0 1 2 2 3 1 1 9 3 1 3 1 0 1 0 0 0]

Il est possible «d'étrangler» encore plus la maladie; par exemple, laissons$$$\beta=0.01$mais mettez $$$\mu=0.5$, c'est-à-dire qu'à chaque intervalle de temps, chaque malade a une chance de guérir de 0,5 (au final, c'est logique: soit il va guérir, soit non). Alors seulement 50 à 60 personnes sur 100 tomberont malades du terrible virus; les courbes peuvent ressembler à ceci:

[1 0 0 1 3 2 1 1 0 3 0 0 0 0 0 1 0 0 0 0 0]

Mais le tableau d'ensemble, bien sûr, dans tous les cas est à peu près le même: première croissance exponentielle, puis sortie vers la saturation; la seule différence est de savoir si le dernier opérateur a le temps de récupérer avant que tout le monde ne soit redémarré.



Eh bien, il est temps de résumer les résultats intermédiaires. Aujourd'hui, nous avons vu à quoi ressemble l'un des modèles épidémiologiques les plus simples. Malgré de nombreuses hypothèses simplificatrices à l'extrême, le modèle SIR est toujours très utile même sous cette forme; le fait est que la plupart de ses extensions sont assez simples et ne changent pas l'essence générale de la question. Par conséquent, si nous continuons, dans la prochaine série, je parlerai de la façon de former un modèle SIR; cependant, cela impliquera tellement de choses intéressantes que cela ne rentrera probablement pas non plus dans un seul article. Jusqu'à la prochaine fois!