Quel est l'avenir des mathématiques?
- Dans les années 1990, les ordinateurs ont commencé à jouer aux échecs mieux que les humains.
- En 2018, les ordinateurs sont meilleurs pour jouer à Go que les humains.
- En 2019, le chercheur en intelligence artificielle Christian Szegedy m'a dit que dans 10 ans, les ordinateurs seront mieux à prouver le théorème que les humains.
Bien sûr, il a peut-être tort. Ou peut-être qu'il a raison.
Je crois en ceci: dans dix ans, les ordinateurs nous aideront à prouver des théorèmes mornes au niveau des premiers étudiants diplômés. Quels domaines des mathématiques? Cela dépend de qui s'implique dans ce domaine de recherche.
Le schéma typique de l'intelligence artificielle est le suivant: au début, c'est très stupide, puis cela devient soudainement plus intelligent. La question naturelle est la suivante: quand la transition de phase se produit-elle et l'intelligence artificielle devient-elle soudainement très intelligente? Réponse: personne ne le sait. Ce qui est clair, c'est que plus les gens sont impliqués dans ce domaine de recherche, plus vite cela se produira.
Qu'est-ce que la preuve?
Si vous demandez à un excellent étudiant, à un mathématicien de recherche et à un ordinateur quelle est la preuve, quelle est leur réponse? Les réponses de l'excellent élève et de l'ordinateur coïncideront et seront les suivantes:
Une preuve est une séquence logique d'énoncés, constituée des axiomes du système choisi, des règles d'inférence et des théorèmes qui ont été prouvés précédemment, qui conduisent finalement à la démonstration de l'énoncé.Bien sûr, la réponse d'un mathématicien de recherche ne serait pas aussi idéaliste. Pour un mathématicien, la définition de la preuve est ce que d'autres mathématiciens expérimentés considèrent comme une preuve. Ou ce qui est accepté pour publication dans les Annals of Mathematics ou Inventiones.
Cependant, cela pose un petit problème. Les captures d'écran suivantes proviennent des Annals of Mathematics , l'une des revues mathématiques les plus prestigieuses au monde.
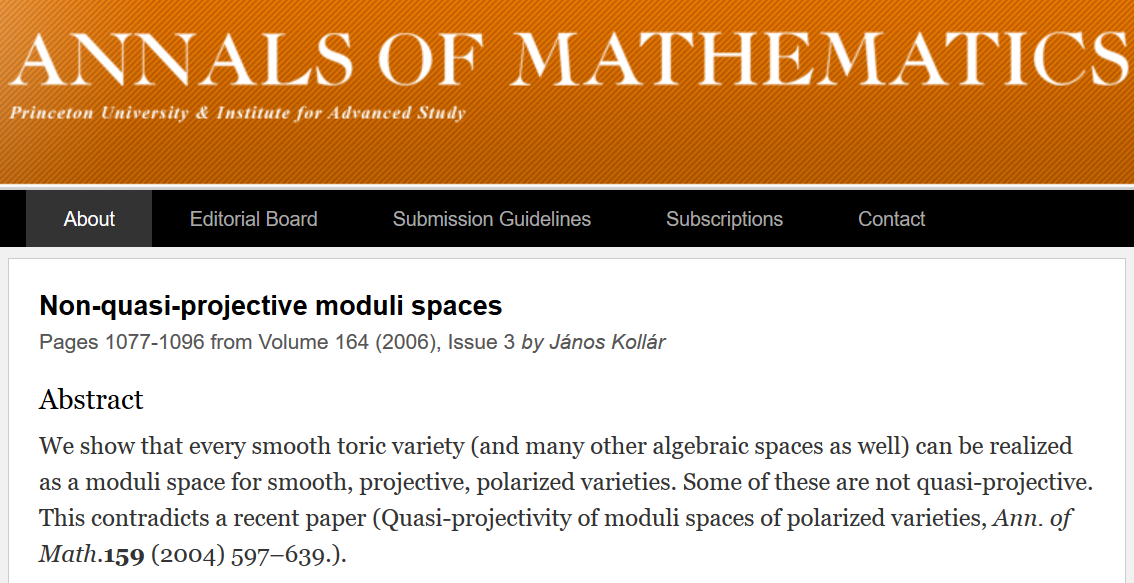
Le deuxième article contredit littéralement le premier. Les auteurs écrivent ouvertement à ce sujet dans l'annotation. Autant que je sache, les Annals of Mathematics n'ont jamais publié de réfutation à aucun de ces ouvrages. Quel travail est considéré comme correct par des mathématiciens expérimentés? Vous ne pouvez le découvrir que si vous travaillez dans ce domaine.
Production: en mathématiques modernes, l'opinion sur la question de savoir si quelque chose est une preuve change avec le temps (par exemple, elle peut passer de «est» à «n'est pas»).
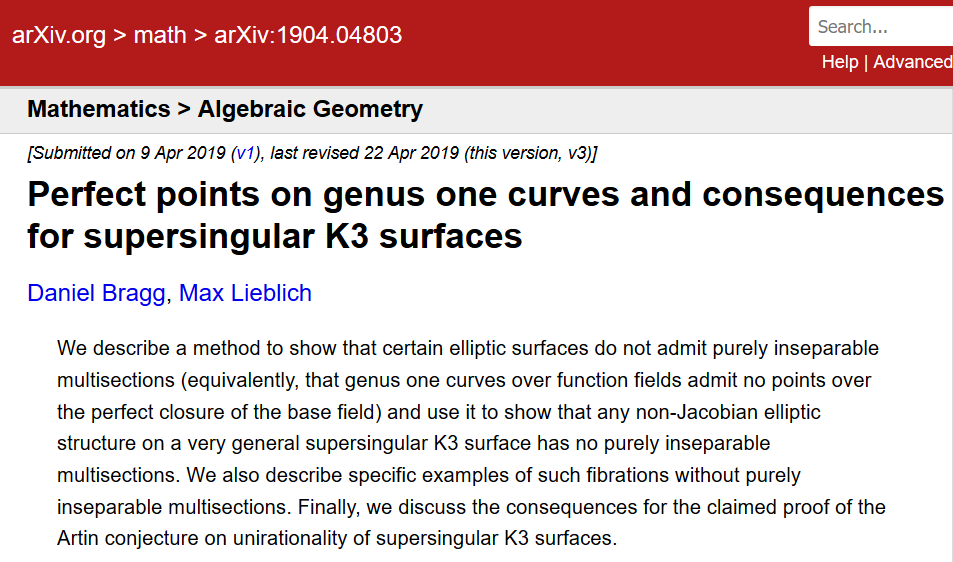
Ce court article de 2019 souligne qu'un autre article important de 2015 publié dans Inventiones repose largement sur un faux lemme. Cela n'a été remarqué qu'en 2019, malgré le fait qu'en 2016, les gens ont organisé des ateliers pour étudier ce travail important.
Vladimir Voevodsky, lauréat du prix Fields qui a contribué aux fondements des mathématiques, écrit que «si un auteur auquel les gens font confiance écrit un argument techniquement complexe qui est difficile à vérifier, mais qui est similaire à d'autres arguments corrects, alors cet argument ne sera presque jamais tout sera vérifié en détail. "
Inventiones n'a jamais publié de réfutation de l'article de 2015.
Conclusion : les calculs importants qui ont été publiés se révèlent parfois erronés. De plus, à l'avenir, nous verrons sûrement plus de réfutations des preuves publiées.
Peut-être que mon travail dans le domaine du programme p-adic de Langlands est basé sur des résultats incorrects. Ou, de façon plus optimiste, pour des résultats corrects, mais pour lesquels il n'y a pas de preuve complète.
Si notre recherche est irreproductible, pouvons-nous l'appeler science? Je suis sûr à 99,9% que le programme p-adic de Langlands ne sera jamais utilisé par l'humanité pour faire quoi que ce soit d'utile. Si mon travail en mathématiques n'est pas utile et garanti à 100% correct, c'est juste une perte de temps.... J'ai donc décidé d'arrêter de chercher et de me concentrer sur le test de mathématiques «célèbres» sur un ordinateur.
En 2019, Balakrishnan, Dogra, Mueller, Tuitman et Vonk ont trouvé toutes les solutions rationnelles à une certaine équation du quatrième degré en deux variables. Explicitement:
Ce calcul a une application importante en arithmétique. La preuve repose largement sur le calcul dans le magma (un système source fermé) utilisant des algorithmes rapides et non référencés. Il serait difficile de porter tout le calcul vers un système open source comme sage. Cependant, personne n'envisage de faire cela.
Ainsi, certaines des preuves restent cachées. Et peut-être restera-t-il caché pour toujours. Est-ce une science?
Lacunes en mathématiques
- 1993 . .
- 1994 , .
- 1995 , , . , , , . , , , .
Que devrait faire un critique qui reçoit un article mathématique pour révision? On fait valoir que le travail du critique consiste à «s'assurer que les méthodes utilisées dans l'article sont suffisamment solides pour prouver le résultat principal de l'article».
Et si les méthodes sont fortes, mais que les auteurs ne le sont pas? C'est ainsi que des situations surviennent lorsque nos preuves sont incomplètes. C'est ainsi que naît le débat pour savoir si nos théorèmes sont réellement prouvés. Ce n'est pas du tout ainsi que nous enseignons les mathématiques à nos élèves.
Bien entendu, les experts savent à quelle littérature on peut faire confiance et laquelle ne le peut pas. Mais dois-je être un expert pour savoir à quelle littérature je peux me fier?
De grandes lacunes en mathématiques
Pièce A
Classification des groupes finis simples . Les experts affirment que nous avons une classification complète des groupes finis simples. Je fais confiance aux experts.
- En 1983, une preuve d'expert de classification a été annoncée.
- En 1994, des experts ont trouvé une erreur (mais ne faisons pas sauter l'éléphant d'une mouche?)
- En 2004, plus de 1000 pages ont été publiées. L'expert de terrain Aschbacher affirme que l'erreur a été corrigée et annonce un plan pour publier 12 volumes de preuves complètes.
- En 2005, seuls 6 des 12 volumes ont été publiés
- En 2010, seuls 6 volumes sur 12 ont été publiés
- En 2017, seuls 6 volumes sur 12 ont été publiés
- En 2018, les 7e et 8e volumes ont été publiés et une note que la publication sera achevée d'ici 2023.
Sur les trois personnes à la tête du projet, une est décédée. Les deux autres ont plus de soixante-dix ans.
Pièce B
Modularité potentielle des surfaces abéliennes . Il y a un an, mon éminent étudiant diplômé Toby Gee et trois coauteurs ont publié une pré-impression de 285 pages montrant que les surfaces abéliennes sur des champs complètement réels sont potentiellement modulaires.
Leur preuve cite trois prépublications non publiées (une en 2018, une en 2015, une dans les années 1990), une note Internet de 2007, une thèse non publiée en allemand et un article dont la thèse principale a été réfutée par la suite. De plus, à la page 13, nous voyons le texte suivant:
, Arthur’s multiplicity formula GSp4, [Art04]. , , [GT18], , [Art13] [MW16a, MW16b]. , twisted weighted fundamental lemma, [CL10], . , [A24], [A25], [A26] [A27] [Art13], .Pouvons-nous honnêtement dire que c'est de la science?
Le lien [CL10] ressemble à ceci: Le
travail dont mon étudiant diplômé et mes coauteurs ont besoin n'a jamais été publié. Très probablement, la déclaration est correcte. Peut-être même prouvable.
Et voici les liens référencés de [Art13]:
L'année dernière, j'ai interrogé Arthur sur ces liens, et il m'a dit qu'aucun des travaux n'était encore prêt. Bien sûr, Jim Arthur est un génie. Il a remporté de nombreux prix prestigieux. Mais il a aussi 75 ans.
Pièce C
Gaitsgory - Rozenblyum . Des catégories infinies ont gagné en popularité ces derniers temps. Ils deviendront encore plus importants avec le temps. Le travail du lauréat Fields Peter Scholze repose sur des catégories infinies.
Jacob Lurie a écrit un travail de plus de 1000 pages sur
-catégorisé et inclus beaucoup de détails dans mon travail. Gaitsgory - Rozenblyum voulait des résultats similaires pour
-categories, mais omis de nombreux arguments pour gagner du temps. "Les preuves omises apparaîtront ailleurs."
J'ai demandé à Gaitsgory combien il manquait. Il a répondu que c'était environ 100 pages. J'ai demandé à Lurie ce qu'il en pensait. Il a répondu que «les mathématiciens diffèrent grandement dans leur aisance à omettre des détails».
Les maths avancent-ils trop vite? Si je suis un «expert», dois-je croire que les surfaces abéliennes sur des champs totalement réels sont potentiellement modulaires? Pour être honnête, je ne me connais plus.
Lors d'une conférence à l'Université Carnegie Mellon, où j'étais la semaine dernière, Markus Rabe m'a dit que Google travaillait sur un programme qui traduira les pré-impressions mathématiques d' arxiv.orgdans une langue adaptée à la vérification informatique. J'ai aussi vu récemment un travail qui s'appuie sur un article de mon élève, mais qui ne mentionne rien sur les 100 pages manquantes dans [Art13].
Dernière erreur
C'est un exemple très intéressant. L'ouvrage original a été publié dans J. Funct. Anal. en 2013. Il y a une grosse erreur dans le travail (inégalité dans l'autre sens). L'erreur a été découverte par S.Gouezel en 2017, lorsque Gouezel a formalisé une argumentation à l'aide d'un programme informatisé de vérification d'épreuves (Isabelle).
Un nouvel argument est présenté par Gouezel et l'auteur de l'œuvre originale. Les nouveaux travaux n'ont pas besoin d'être revus. L'ordinateur a vérifié 100% du nouvel argument. Les méthodes se sont avérées suffisamment solides pour prouver le théorème. Et par «preuve», j'entends la définition classique et «pure» de la preuve - ce que nous enseignons à nos étudiants. Chaque détail de la preuve est à la disposition du lecteur. La science est reproductible. Ce sont les mathématiques que nous enseignons à nos élèves. Ce sont les mathématiques.
Voici d'autres exemples de ce que je pense être des mathématiques:
- Preuve typique de niveau étudiant ou maîtrise
- Preuve typique de 100 ans d'un résultat important qui a été bien documenté et étudié par des dizaines de milliers de mathématiciens
- Preuve formelle de Gonthier, Asperti, Avigad, Bertot, Cohen, Garillot, Le Roux, Mahboubi, O'Connor, Ould Biha, Pasca, Rideau, Solovyev, Tassi, Théry du théorème de Feith-Thompson.
- Preuve formelle de la paternité par les mathématiciens suivants: Hales, Adams, Bauer, Dat Tat Dang, Harrison, Truong Le Hoang, Kaliszyk, Magron, McLaughlin, Thang Tat Nguyen, Truong Quang Nguyen, Nipkow, Obua, Pleso, Rute, Solovyev, An Hoai Thi Ta , Trung Nam Tran, Diep Thi Trieu, Urban, Ky Khac Vu et la preuve de Zumkeller de la conjecture de Kepler.
Ceci conclut le texte de la présentation, car Kevin passe à sa partie principale: la vérification formelle des preuves mathématiques en Lean, développée par Leo de Moura chez Microsoft Research. Malheureusement, les exemples n'ont pas été inclus dans les diapositives.
L'auteur est un grand passionné de vérification formelle des preuves mathématiques et a un blog Xena très intéressant sur ce sujet que je recommande vivement.