Bonjour les Habitants! Un colosse aux pieds d'argile est ce que vous pouvez appeler un programmeur sans formation en informatique. Une maîtrise sûre des bases permet de ne pas «réinventer la roue» et d'intégrer des solutions efficaces dans l'architecture logicielle. Tout cela élimine les erreurs et les coûts excessifs de test et de refactorisation.
Peu importe que vous vous sentiez déplacé lorsque d'autres programmeurs discutent de la limite approximative. Même les experts expérimentés font des erreurs parce qu'ils ont oublié l'informatique.
Pourquoi ce livre est nécessaire
Beaucoup de mes collègues développeurs (de l'auteur) sont venus dans la profession dans une grande variété de domaines. Certains ont une formation supérieure en informatique; d'autres ont étudié la photographie, les mathématiques ou n'ont même pas obtenu de diplôme universitaire.
Ces dernières années, j'ai remarqué que les programmeurs sont de plus en plus désireux d'apprendre l'informatique pour plusieurs raisons:
- devenir de bons programmeurs;
- pour répondre aux questions sur les algorithmes lors des entretiens;
- pour satisfaire leur curiosité pour l'informatique, ou enfin pour arrêter de regretter qu'à un moment donné ils n'aient pas eu l'occasion de maîtriser ce sujet.
Ce livre est pour vous tous.
Beaucoup trouveront ici des sujets intéressants en eux-mêmes. J'ai essayé de montrer dans quelles situations réelles (non académiques) ces connaissances seront utiles. Après avoir lu ce livre, je souhaite que vous acquériez les mêmes connaissances qu'après avoir étudié le cours de base en informatique et que vous appreniez également à l'appliquer.
En termes simples, le but de ce livre est de vous aider à devenir un programmeur plus qualifié et expérimenté grâce à une meilleure compréhension de l'informatique. Je ne peux pas regrouper 20 ans d'enseignement universitaire et d'expérience professionnelle dans un seul livre ... mais je vais essayer de faire de mon mieux. J'espère que vous trouverez ici au moins un sujet sur lequel vous pourrez dire: «Oui, maintenant je comprends cela» et appliquer les connaissances dans votre travail.
Ce que vous ne trouverez pas dans l'édition
Le sens du livre est d'aider le lecteur à mieux comprendre l'informatique et à appliquer les connaissances dans la pratique, et pas du tout à remplacer complètement quatre années d'études.
En particulier, ce n'est pas un livre de preuves. En effet, dans le deuxième volume de l' ouvrage , des méthodes de preuve sont envisagées, mais les algorithmes standards sont généralement présentés ici sans preuve. L'idée est que le lecteur connaisse l'existence de ces algorithmes et apprenne à les utiliser sans entrer dans les détails. En tant que livre de preuve écrit pour les étudiants de premier cycle et des cycles supérieurs, je recommande vivement Introduction aux algorithmes de Cormen, Leiserson, Rivest et Stein (les auteurs sont généralement regroupés sous abréviation CLRS).
Ce n'est pas non plus un livre de programmation: vous ne trouverez pas de directives sur quand utiliser des nombres de type int et quand utiliser double, ni d'expliquer ce qu'est une boucle. On s'attend à ce que le lecteur soit capable de comprendre les listes de pseudocodes utilisées pour décrire les algorithmes (tous les programmes de ce livre sont écrits en pseudo-code basé sur le langage C). Le but du livre est de relier les concepts de l'informatique avec des techniques de programmation déjà familières au lecteur.
10. Programmation dynamique
10.1. Problème de champs manquants
Supposons que nous ayons un échiquier n × n manquant plusieurs carrés. Comment trouver le plus grand morceau de carton k × k sans champs manquants?
Si vous n'avez jamais rencontré un tel problème auparavant, prenez quelques minutes pour écrire une solution et déterminer le temps d'exécution de votre algorithme.
Face à ce problème, j'ai raisonné comme suit. Chaque champ en damier peut appartenir à la plupart des plus grandes zones, mais seulement dans l'un d'entre eux, il peut être le coin supérieur gauche. Si je marque chaque case avec la taille de la plus grande zone intacte dont c'est le coin supérieur gauche, alors le champ avec la plus grande marque de ce type correspondra à la zone souhaitée.
Supposons que la carte soit représentée comme une matrice n × n dans laquelle chaque cellule contient 1 si le champ correspondant est présent et 0 s'il est manquant. Si la valeur de cellule actuelle est 0, le champ correspondant est absent et ne peut pas faire partie d'un segment contigu, il n'a donc pas besoin d'être modifié. Si la valeur est 1, nous pouvons la remplacer par un nombre supérieur de un à la valeur minimale des trois cellules situées en dessous et à droite.
Nous modifions chaque cellule de la matrice une fois, notamment en vérifiant si la valeur de la cellule est égale à zéro, en vérifiant les valeurs de trois autres cellules au maximum et en écrivant la nouvelle valeur de cellule. Chacune de ces opérations prend O (1) temps, donc le temps nécessaire pour traiter l'ensemble du damier est
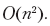
Notez qu'il s'agit d'un temps d'exécution linéaire et non quadratique de l'algorithme - sur un échiquier n (nous supposons que n est le nombre total de champs, et nous adhérons à la convention habituelle selon laquelle n est la quantité de données d'entrée) champs (certains d'entre eux sont absent), donc le temps total passé par l'algorithme est proportionnel au nombre de champs. Si nous désignons plus précisément la taille de l'échiquier par √ n × √ n, alors nous obtenons n champs et le temps total d'exécution est O (n).
10.2. Travailler avec des sous-tâches qui se chevauchent
L'approche utilisée dans cette section est appelée programmation dynamique. Il est utilisé lorsqu'un problème peut être divisé en plusieurs sous-tâches, dont la solution de chacune sera utilisée plusieurs fois. Cette approche diffère du principe de «diviser pour vaincre», lorsque le problème est divisé en sous-tâches, qui sont résolues indépendamment les unes des autres. Dans le problème de l'échiquier, chaque sous-problème dépendait des solutions à trois autres problèmes, et les solutions à tous les sous-problèmes ont été enregistrées pour une utilisation ultérieure.
La programmation dynamique est généralement effectuée en créant des tableaux comme indiqué ci-dessus. Cela signifie résoudre un problème en utilisant une approche ascendante, où nous commençons par résoudre les plus petits sous-problèmes et progressons jusqu'à ce que nous arrivions à une réponse. Une autre méthode est la mémorisation, où nous allons de haut en bas, résolvant les sous-problèmes au besoin et mettant en cache les résultats pour les réutiliser. Construire des tables est l'option préférée lorsque vous devez résoudre chaque sous-problème (dans mon exemple avec un échiquier, il était nécessaire de trouver la plus grande surface intacte pour chaque champ du plateau), car les coûts de cette méthode sont inférieurs à ceux de la mémorisation. Si certaines sous-tâches de la zone de solution n'ont pas à être résolues, la mémorisation vous permet de résoudre uniquement les sous-tâches qui sont vraiment nécessaires.
Le point clé
Lorsque diviser et conquérir implique de diviser une tâche en plusieurs sous-tâches indépendantes, la programmation dynamique signifie diviser une tâche en plusieurs sous-tâches qui se chevauchent. La solution à chaque sous-problème est mise en cache pour une réutilisation ultérieure.
10.3. Programmation dynamique et chemins les plus courts
Considérez le problème de trouver le chemin le plus court: pour un graphe donné avec des arêtes pondérées, vous devez trouver un chemin d'un nœud à un autre qui a le coût le plus bas.
Définition Un
graphe pondéré par les bords est un graphe dans lequel chaque arête a son propre poids (coût). Le coût d'un chemin d'un nœud à un autre est déterminé par la somme du coût de tous les bords traversés.
Supposons que nous trouvions un chemin entre les nœuds s et t contenant le troisième nœud v. Ensuite, le chemin de s à t doit contenir le chemin le plus court de s à v, car sinon nous pourrions remplacer ce segment par un chemin plus court et réduire la longueur du chemin le plus court de s à t, ce qui contredit la condition initiale (c'est le principe d'optimalité de Bellman).
( ) , . , . , .
, , .
Les problèmes de trouver le chemin le plus court sont des exemples frappants de programmation dynamique, car la propriété optimale d'une sous-structure est intuitivement claire - il est évident que le moyen le plus rapide d'aller du point A au point C en passant par le point B est aussi le moyen le plus rapide d'aller du point A au point B et du point B au point C.Le nombre d'algorithmes basés sur ce principe inclut la méthode Bellman - Ford, qui trouve le chemin le plus court du point de départ à n'importe quel sommet du graphe (ou de n'importe quel sommet du graphe au point final) et la méthode Floyd - Warshall - avec son aide le chemin le plus court entre chaque paire de sommets du graphe est calculé. Dans les deux cas, l'idée est de commencer avec un petit sous-ensemble de nœuds proches des nœuds d'intérêt, et d'étendre progressivement cet ensemble en utilisant les nœuds déjà trouvés pour calculer de nouvelles distances.
10.4.
10.4.1. Git merge
Une autre tâche couramment utilisée pour démontrer la programmation dynamique consiste à trouver la sous-séquence commune la plus longue. La tâche est de trouver, pour deux chaînes A et B données, la séquence la plus longue qui se produit dans les deux chaînes, en conservant la séquence de caractères. Les chaînes ne doivent pas être dans une rangée; par exemple, si A = {acdbef} et B = {babdef}, alors {adef} sera leur sous-séquence commune.
Lors de la fusion des modifications dans Git (fusion), il recherche la plus grande sous-séquence commune pour les branches maître et de travail. Les caractères présents dans le maître mais non présents dans la plus grande sous-séquence commune sont supprimés; les caractères qui sont dans la branche de travail mais qui ne sont pas dans cette sous-séquence sont ajoutés au maître.
10.4.2. LATEX
Le système de préparation de documents LATEX est souvent utilisé pour créer des documents techniques. L'une des tâches du système de saisie est d'aligner le texte à droite et à gauche en même temps; pour ce faire, les espaces entre les mots et les caractères sont étirés ou réduits pour que toutes les lignes aient la même longueur. Une autre façon d'aligner le texte consiste à envelopper le dernier mot afin qu'une partie du mot apparaisse sur la ligne suivante. LATEX (D'un point de vue technique, le système de saisie de texte TEX fait presque tout le travail; LATEX est construit sur TEX. Ici, j'utilise LATEX pour des raisons de simplicité) essaie de trouver des points de rupture de ligne optimaux pour rendre le texte agréable. En cas d'échec, plusieurs lignes d'affilée se termineront par un trait d'union, ou la distance entre les mots de différentes lignes sera différente.LATEX a un ensemble de règles pour évaluer l'échec d'alignement. Le programme cherche à trouver l'option «la moins mauvaise».
S'il y a n points de saut de ligne possibles dans un paragraphe, il existe
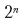des options possibles pour couper le texte. L '«échec» de la sélection pour chaque point d'arrêt dépend des points d'arrêt sélectionnés avant lui. Par conséquent, nous avons à nouveau des sous-tâches qui se chevauchent. L'utilisation de techniques de programmation dynamique réduit le temps d'exécution 
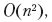auquel il est possible d'améliorer avec des méthodes supplémentaires.
»Plus de détails sur le livre peuvent être trouvés sur le site de l'éditeur
» Table des matières
» Extrait
Pour Habitants un rabais de 25% sur le coupon - Informatique
Dès le paiement de la version papier du livre, un e-book est envoyé à l'e-mail.