Détecteur de chauves-souris à ultrasons hétérodyne

Petite chauve-souris en fer à cheval



Ce projet décrit la création de la soi-disant. détecteur de chauve-souris - un appareil qui vous permet d'entendre et d'enregistrer les sons émis par les chauves-souris. Vous savez probablement que les chauves-souris émettent des ultrasons pour l'écholocation. La fréquence de ces sons est hors de la plage perceptible par l'oreille humaine, ils ne peuvent donc pas être entendus directement. Le détecteur de chauve-souris utilise un microphone spécial capable de capter ces sons haute fréquence et de les convertir en son qui se situe dans la plage audible.



Il existe trois types de détecteurs de chauves-souris . Pour moi j'ai fait un hétérodynedétecteur. Son inconvénient est qu'il est plus difficile de distinguer différents types de chauves-souris par rapport à l'enregistrement de sons à haute fréquence. J'expliquerai plus tard comment fonctionne un détecteur hétérodyne, mais regardons d'abord le microphone nécessaire pour enregistrer les ultrasons.



Lors du choix d'un microphone, j'ai d'abord envisagé deux options:

- un microphone à électret - tout ce que j'ai trouvé, selon les documents, ne fonctionne que dans la plage de 10 à 20 kHz, mais si vous en croyez certaines ressources, certains de leurs types perçoivent également les ultrasons dans une certaine mesure. Cependant, comme leurs descriptions officielles ne l'indiquent pas, il faudrait beaucoup d'essais et d'erreurs pour parcourir les différentes marques et les essayer. J'ai donc abandonné ce type de micro.

- capteurs piézoélectriques... On les trouve, par exemple, dans les télémètres à ultrasons HC-SR04 populaires, qui sont omniprésents et bon marché. Leur inconvénient est que leur sensibilité est très proche de la fréquence de résonance, quelque part autour de 40 kHz. Et en s'éloignant de cette fréquence, la sensibilité baisse fortement. Donc, ils ne correspondent pas non plus.



Au lieu de cela, j'ai fini par trouver un microphone Knowles SPU0410LR5H , un microphone de type MEMS... Selon la spécification, ce microphone a une courbe de réponse assez plate à toutes les fréquences jusqu'à 80 kHz, il est donc très bien adapté à ce projet. De plus, il dispose d'un préamplificateur interne à haut S / N. Le principal inconvénient de ce microphone est que son boîtier n'est pas destiné à des projets artisanaux. Il est minuscule (3,76 x 3 mm!), Et ses contacts sont à l'intérieur du boîtier. J'ai cherché sur Internet et suis tombé sur la page de l' utilisateur de hackaday.io Alan Green, qui a également utilisé ce microphone dans son projet. Il a eu une bonne idée de créer une carte spéciale pour ce microphone, afin qu'il puisse être soudé manuellement. Le but est d'allonger les coussinets pour qu'ils dépassent du composant. J'ai pris cette idée et conçu une petite carte pour un microphone et un double ampli op. Ce dernier fournit une masse virtuelle (à la moitié de la tension d'alimentation), ainsi qu'un étage d'amplification de 20 dB (soit 10 fois). Au début, j'étais sceptique quant à la soudure de ce microphone à la main, mais tout fonctionnait bien - les 6 cartes que j'ai soudées ont réussi. J'ai enregistré une vidéo de la soudure pour clarification. La conception des panneaux est également rendue publique .



















Commençons par expliquer le principe de fonctionnement d'un détecteur de chauves-souris hétérodyne. Commençons par regarder les signaux émis par les souris. Ils peuvent être modélisés comme une fréquence porteuse ultrasonore modulée en amplitude et un signal d'enveloppe comme un "chirp" court est le signal (un signal avec modulation de fréquence linéaire ).







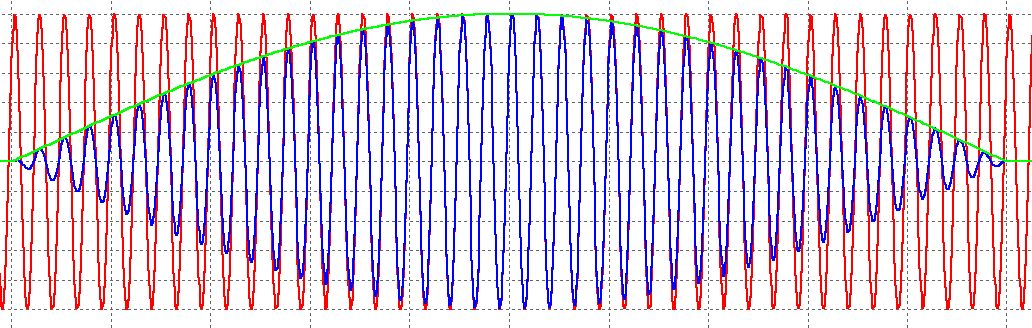
Dans le diagramme échographique, la porteuse est représentée en rouge, l'enveloppe du bip est affichée en vert et la somme totale est affichée en bleu. Pour traduire le signal dans la plage audible par l'homme, vous devez le convertir de manière à préserver l'enveloppe (chirp), en la modulant avec un signal porteur avec une fréquence inférieure (par exemple, dans la plage de 1 à 5 kHz). Comment cela peut il etre accompli?



Pour comprendre comment cela se fait d'un point de vue mathématique, nous utilisonsidentités trigonométriques connues :



2sin (x) ⋅sin (y) = cos (x - y) −cos (x + y)

2cos (x) ⋅cos (y) = cos (x - y) + cos (x + y)

2sin (x) ⋅cos (y) = sin (x - y) + sin (x + y)

2cos (x) ⋅sin (y) = - sin (x - y) + sin (x + y)



Si nous prenons notre modèle de signal des chauves-souris, il peut être modélisé comme suit:



porteuse (t) = sin (2πf _c t)

chirp (t) = sin (2πf _chirp t)

bat (t) = porteuse (t) ⋅chirp (t)



où est la fréquence ultrasonique porteuse - f _c et la fréquence du signal chirp - f _chirp . Pour cet exemple, supposons:



f _c = 40 kHz

f _chirp = 1 kHz



En appliquant les identités trigonométriques, nous obtenons:



bat (t) = sin (2πf _c t) ⋅sin (2πf _chirp t) = 1/2 cos (2π (f _c −f _chirp ) t) - 1/2 cos (2π (f _c + f _chirp ) t)



Le signal modulé se compose de deux fréquences situées symétriquement autour de la fréquence porteuse, dans cet exemple



40 kHz - 1 kHz = 39 kHz

40 kHz + 1 kHz = 41 kHz



C'est le LSB inférieur et la bande latérale USB supérieure :



f _LSB = f _c −f _chirp

f _USB = f _c + f _gazouillis



Nous pouvons maintenant utiliser le même principe pour convertir le signal de la souris en une fréquence audible inférieure. Pour ce faire, vous devez multiplier le signal par la fréquence du générateur local LO - c'est la différence entre la fréquence porteuse du signal et la fréquence porteuse souhaitée (dans notre cas, la fréquence audible à laquelle nous aimerions entendre les cris des chauves-souris). Cette technique s'appelle l' hétérodynage.Dans notre exemple, disons que nous voulons entendre les cris de souris à une fréquence de 5 kHz, ce qui est bon pour l'homme. Alors:



f _cible = 5 kHz

f _LO = f _c −f _cible = 35 kHz

LO (t) = sin (2πf _LO t)



En mettant tout cela ensemble, nous pouvons réécrire les termes des équations en utilisant des identités trigonométriques:



bat (t) ⋅LO (t) = (1/2 cos (2πf _LSB t) −1/2 cos (2πf _USB t)) ⋅sin (2πfLOt)

= 1 / 2cos (2πf _LSB t) ⋅sin (2πf _LO t) - 1 / 2cos (2πf _USB t) ⋅sin (2πf _LO t)

= 1/4 (sin (2π (f _LO −f _LSB ) t) + sin (2π (f _LO + f _LSB ) t) - sin (2π (f _LO −f _USB ) t) - sin (2π (f _LO + f _USB ) t))



(en considérant que sin (−x) = - sin (x)),



= 1/2 (−1 / 2sin (2π (f _LSB −f _LO) t) + 1 / 2sin (2π (f _USB −f _LO ) t) + 1 / 2sin (2π (f _LSB + f _LO ) t) - 1 / 2sin (2π (f _USB + f _LO ) t))

= 1/2 (−1 / 2sin (2π (fc - f _LO -f _chirp ) t) + 1 / 2sin (2π (fc - f _LO + f _chirp ) t) + 1 / 2sin (2π (fc + f _LO - f _chirp ) t) - 1 / 2sin (2π (fc + f _LO + f _chirp ) t))

= 1 / 2cos (2πf _cible t) ⋅sin (2πf _chirp t) + 1 / 2cos (2πf ₂ t) ⋅sin (2πf _chirp t)



On voit que le premier terme, cos (2πf _cible t) ⋅sin (2πf_chirp t) est exactement ce que nous voulons, une enveloppe chirp modulée avec une fréquence audible de 5 kHz. Le deuxième terme est à nouveau un signal de chirp modulé à une fréquence plus élevée, f ₂ = f _c + f _LO , dans ce cas 75 kHz. Le deuxième composant est bien en dehors de la plage audible et est facilement coupé par le filtre passe-haut dans le circuit du détecteur de chauve-souris.



Maintenant que nous avons une compréhension théorique de la façon dont le principe d'hétérodynage peut être utilisé pour construire un détecteur de chauve-souris - comment le mettre en pratique? L'essentiel est de multiplier le signal d'entrée par le signal LO, ce qui dans l'électronique pratique n'est pas si facile à faire. Il existe des circuits pour la multiplication analogique (par exemple, la cellule de Gilbert), et nous pouvons utiliser un CI approprié (tel que NE612 ) en conjonction avec un générateur d'onde sinusoïdale (par exemple, un générateur de pont de Wien ). Cependant, une telle solution sera difficile et les CI pour la multiplication analogique tels que NE612 ou similaire sont rares et coûteux.



Il s'avère qu'il existe une option plus simple et qu'elle peut être assemblée à partir de composants standard courants. Nous pouvons assembler un mélangeur de fréquence avec commutation analogique. Bien que ce ne soit pas un mélangeur parfait, puisqu'il ne multiplie pas réellement les deux signaux, nous verrons bientôt qu'il fonctionne toujours assez bien.



Pour l'instant, jetons un œil aux diagrammes et essayons de comprendre comment cela fonctionne.







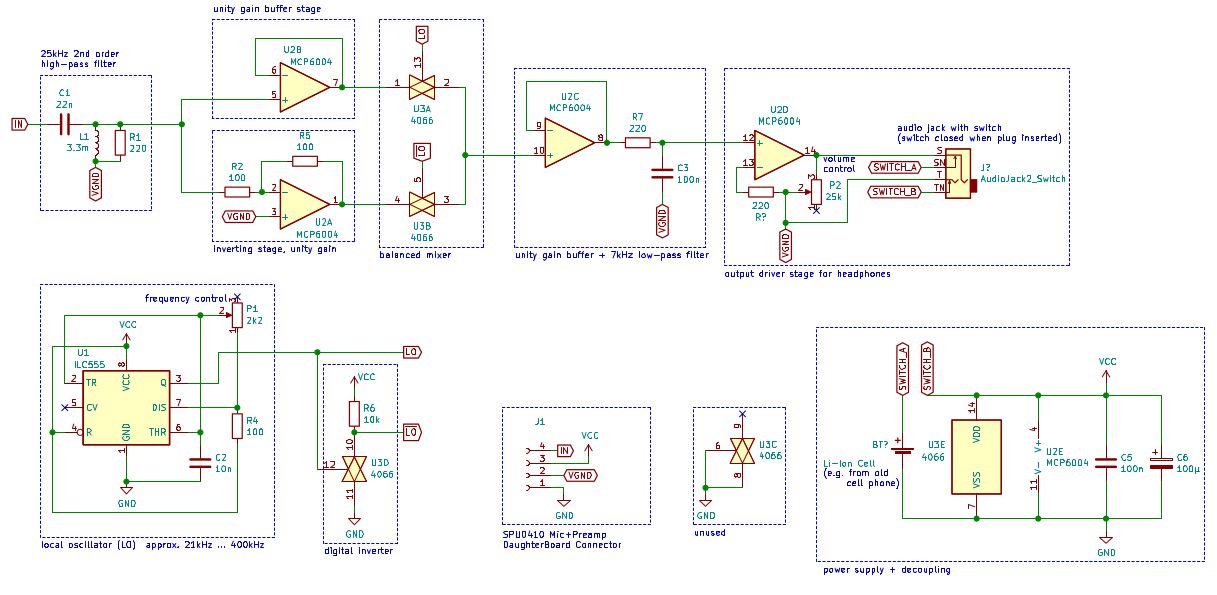
Sur la gauche du diagramme, la sortie microphone est envoyée à un filtre LC passe-haut du deuxième ordre, qui supprime les fréquences audibles inférieures à 20 kHz, et ne permet que les ultrasons de passer (puisque c'est ce dont nous avons besoin). La résistance R1, parallèle à l'inducteur, est nécessaire - elle amortit la résonance.



Après le filtre passe-haut, le signal arrive à deux étages d'amplificateurs opérationnels, avec des coefficients 1 et -1 (c'est-à-dire qu'il inverse le signal). Nous avons maintenant à la fois le signal de la souris et son homologue inversé.



En bas à gauche du schéma, vous pouvez reconnaître un multivibrateur bistable avec le fameux IC 555... Le potentiomètre P1 peut surveiller l'ensemble du circuit et créer une onde carrée avec un rapport cyclique d'environ 50% et une fréquence variable de 20 kHz à 400 kHz. Dans notre cas, ce sera le signal de l'oscillateur local LO, mais contrairement à notre modèle mathématique, cette onde est carrée et non sinusoïdale. Le signal LO arrive à l'étage inverseur, qui se compose d'un interrupteur analogique U3D et d'une résistance R6. Ici, le commutateur analogique est utilisé comme onduleur numérique, et comme le CD4066 IC possède 4 commutateurs analogiques, nous en avons deux de rechange, dont l'un peut être utilisé comme onduleur et économiser sur les composants. Cela fonctionne simplement: si le signal LO est faible, le commutateur est ouvert et R6 tire le signal de sortie du commutateur vers le haut. Si le signal est haut, la clé est fermée et la sortie de la clé est reliée à la masse. C'est ainsi qu'un signal inversé est obtenu.$$$\overline{LO}$ .



Regardons maintenant la partie du circuit intitulée «table de mixage équilibrée». Le signal de souris non inversé est envoyé à un commutateur analogique qui contrôle le signal LO. Le signal inversé est transmis à une autre touche, qui contrôle le signal$$$\overline{LO}$ . Les principales sorties sont connectées. Que fait cette partie du circuit?



Considérons le cas où le signal LO est 0 (bas) et donc le signal$$$\overline{LO}$ 1 (élevé). Dans ce cas, la touche inférieure U3B est fermée et la touche supérieure U3A est ouverte. Par conséquent, un signal de souris inversé passe à travers. Dans le cas contraire, lorsque le signal LO est 1 (haut), et donc le signal$$$\overline{LO}$ 0 (bas)., L'interrupteur inférieur U3B est ouvert et fermé supérieur U3A. Puis le signal non inversé passe. Rappelons que cette commutation se produit à une fréquence f_LOdéterminée par la boucle de temporisation 555.



Ce comportement peut-il être modélisé mathématiquement? Essentiellement, ce circuit mélangeur multiplie le signal par une onde carrée qui bascule entre +1 et -1. Cela équivaut à commuter le signal de sortie entre inversé et non inversé. Une telle onde (appelons-la r (t)) peut être décrite par le soi-disant.avec la fonctionsigne (x):

$$

$$r(t):=sign(sin(2πft)), \; \; sign(x)= \begin{cases} 1 &\text{x >= 0} \\ -1 &\text{x < 0} \end{cases}$$

Par conséquent, en sortie du mélangeur, on obtient le produit bat (t) ⋅r (t). En soi, cela n'explique encore rien - pour comprendre comment se produit le mélange de fréquences, nous devons appliquer une magie mathématique appelée l'expansion des séries de Fourier. Je vous épargnerai la conclusion et vous donnerai le résultat immédiatement. En fait, en utilisant la série de Fourier, on peut montrer que:







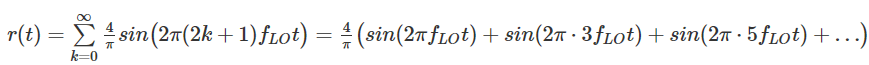
Notre onde carrée + 1 / -1 est donc constitué d'un ensemble infini de sinusoïdes de fréquence fondamentale f _LO et de ses facteurs impairs. Qu'est-ce qui en découle? Si vous ignorez la constante 4 / π, vous pouvez voir que r (t) est la somme de LO (t) et d'autres fréquences supérieures supplémentaires LO ₃ (t), LO ₅ (t), et ainsi de suite. À partir de calculs précédents, nous avons montré que:







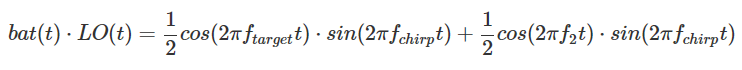
Par conséquent, il peut être calculé que:







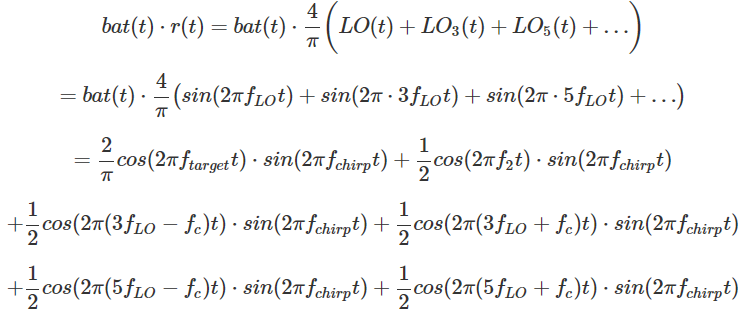
Nous voyons à nouveau que le premier terme 2 / π cos (2πf _cible t) ⋅sin (2π f _chirp t) est ce que nous voulons, mais avec notre mélangeur commutable analogique imparfait, nous nous retrouvons avec un tas d'autres termes inutiles. Cependant, toutes ces composantes de fréquence inutiles ont des fréquences beaucoup plus élevées que notre cible f _cible . On peut donc utiliser un filtre passe-haut pour éliminer ces composantes, et obtenir un signal final approximativement égal à 2 / π cos (2π f _cible t) ⋅sin (2π f _chirp t).



Si nous revenons au circuit, la sortie du mélangeur arrive à l'étage tampon, puis au filtre RC passe-bas avec une fréquence de couplage de ~ 7 kHz. Le dernier étage d'amplification fournit un gain réglable et sert de pilote de sortie (par exemple, un casque).



Pour mieux comprendre le fonctionnement du mixage de fréquences, j'ai réalisé un simulateur de circuit dans LTSpice . Vous pouvez télécharger les fichiers de simulation et jouer avec eux.



Quelques notes sur les composants. Je voulais que tout le circuit soit alimenté par une seule batterie lithium-ion car j'en ai un tas de vieux téléphones et autres. Par conséquent, l'ensemble du circuit doit fonctionner avec une alimentation de 3 à 4 V.Par conséquent, la minuterie 555 et le commutateur analogique 4066 doivent être sélectionnés comme CMOS - ils fonctionnent déjà à 3 V. J'ai utilisé le CD4066B et l'ILC555. Un ampli-op quad doit également fonctionner à basse tension; J'ai choisi le MCP6004, que j'utilise beaucoup.



Je n’ai pas posé la carte, mais tout soudé sur la planche à pain. Si vous souhaitez créer votre propre appareil avec une carte, téléchargez le diagramme pour KiCAD... J'ai imprimé le boîtier de l'appareil et les boutons pour régler le volume et la fréquence sur une imprimante 3D. L'appareil se met automatiquement sous tension lorsque vous insérez le casque dans la prise. Une LED rouge clignotante indique la mise sous tension. La carte microphone est située à l'intérieur du boîtier, derrière un petit trou (illustré à droite).







Pour calibrer l'échelle de fréquence, j'ai vérifié la sortie 555 sur un oscilloscope et marqué les fréquences sur le boîtier. Ensuite, j'ai dessiné l'échelle sur l'ordinateur et je l'ai imprimée.



Et c'est ce que nous attendions tous. À quoi ressemble le cri des chauves-souris sur un détecteur? Je vous propose un enregistrement d'un fragment que j'ai enregistré vers 22 heures quand j'ai vu le LM voler à côté d'une lanterne dans le parc. La fréquence est ajustée à 40-45 kHz.







Pour enregistrer le son, j'ai tenu mon smartphone à côté des écouteurs du détecteur, mais cela semblait très idiot, alors j'ai décidé de chercher une meilleure option. Il s'est avéré que la plupart des smartphones ont une entrée microphone dans la prise casque - il vous suffit d'utiliser une broche de 3,5 mm avec 4 contacts. Par conséquent, j'ai développé un adaptateur qui permet de connecter le détecteur à l'entrée microphone d'un smartphone et un casque à la sortie casque du smartphone. Pour que le smartphone reconnaisse qu'un microphone y est branché, une résistance de 2,2 kΩ est nécessaire et un condensateur de 3,3 μF est nécessaire pour découpler le signal.











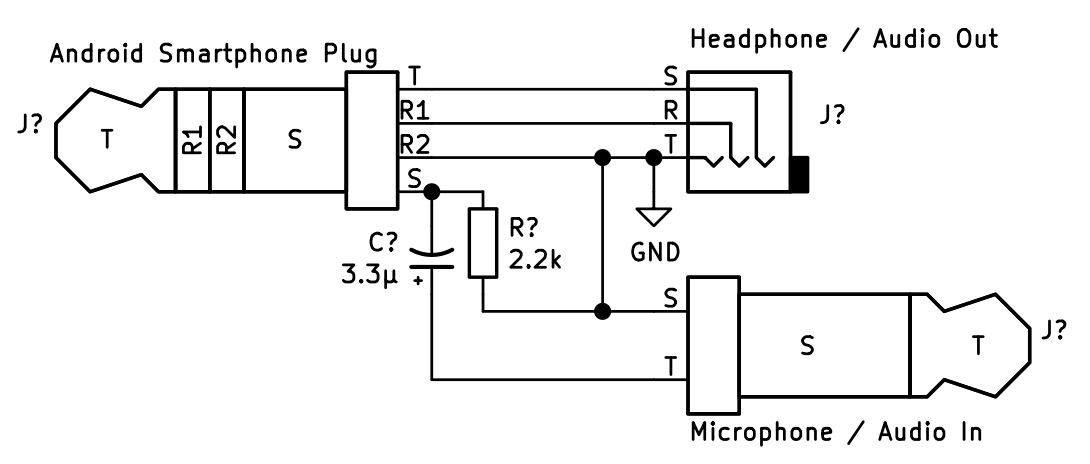
J'ai également dû chercher une application capable d'enregistrer et de lire de l'audio en même temps afin de pouvoir écouter les sons enregistrés en temps réel. J'étais satisfait de l' application RecForge II , bien qu'il y en ait probablement d'autres.



Si vous souhaitez construire votre propre détecteur LM hétérodyne et avez besoin d'un microphone MEMS à ultrasons prêt à l'emploi à bord, vous pouvez le trouver ici:

• Boutique ELV
• Boutique MicBooster

Il n'y a pas d'ampli opérationnel sur ces cartes, vous devrez donc en créer un également. Le reste des ingrédients sera facile à trouver dans votre magasin préféré.

Voir également:

• " Transmission du son par modulation d'amplitude des ultrasons "
• " Module d'un télémètre ultrasonique sous-marin "