Bonjour, je m'appelle David, et me voici, rendu par mon propre rendu peint à la main:





Malheureusement, je n'ai pas pu trouver un modèle gratuit de meilleure qualité , mais j'exprime quand même ma gratitude au sculpteur d'outre-mer qui m'a capturé en numérique! Et comme vous l'avez peut-être deviné, nous parlerons de l'écriture d'un rendu CPU.

Idée

Avec le développement des langages de shader et l'augmentation de la puissance du GPU, de plus en plus de gens s'intéressent à la programmation graphique. De nouvelles directions sont apparues, comme Ray marchant avec une croissance rapide de sa popularité.



En prévision de la sortie d'un nouveau monstre de NVidia, j'ai décidé d'écrire mon propre article (tube et old-school) sur les bases du rendu sur un CPU. C'est le reflet de mon expérience personnelle de l'écriture d'un rendu, et j'essaierai de transmettre les concepts et les algorithmes que j'ai rencontrés pendant le processus de codage. Il faut comprendre que les performances de ce logiciel seront très faibles en raison de l'inaptitude du processeur à effectuer de telles tâches.



Le choix du langage est tombé au départ sur c ++ ou rust , mais je me suis installé sur c #grâce à la facilité d'écriture du code et aux nombreuses possibilités d'optimisation. Le produit final de cet article sera un rendu capable de produire des images comme celle-ci:







Tous les modèles que j'ai utilisés ici sont distribués dans le domaine public, ne piratez pas et respectez le travail des artistes!

Mathématiques

Il va sans dire où écrire des rendus sans en comprendre les fondements mathématiques. Dans cette section, je ne couvrirai que les concepts que j'ai utilisés dans le code. Je ne conseille pas à ceux qui ne sont pas sûrs de leurs connaissances de sauter cette section, sans comprendre ces bases, il sera difficile de comprendre la suite de la présentation. J'espère également que celui qui a décidé d'étudier la géométrie de calcul aura des connaissances de base en algèbre linéaire, en géométrie, ainsi qu'en trigonométrie (angles, vecteurs, matrices, produit scalaire). Pour ceux qui veulent mieux comprendre la géométrie computationnelle, je peux recommander le livre de E. Nikulin "Computer Geometry and Computer Graphics Algorithms" .

Le vecteur tourne. Matrice de rotation

La rotation est l'une des transformations linéaires de base de l'espace vectoriel. C'est aussi une transformation orthogonale, car elle préserve les longueurs des vecteurs transformés. Il existe deux types de rotations dans l'espace 2D:

• Rotation par rapport à l'origine
• Rotation sur un point

Ici, je ne considérerai que le premier type, car le second est un dérivé du premier et ne diffère que par le changement du système de coordonnées de rotation (nous analyserons plus en détail le système de coordonnées).



Dérivons des formules pour faire pivoter un vecteur dans un espace bidimensionnel. Notons les coordonnées du vecteur original - {x, y} . Les coordonnées du nouveau vecteur, tournées de l'angle f , seront notées {x 'y'} .





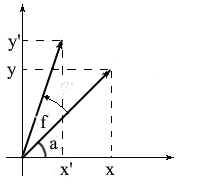
On sait que la longueur de ces vecteurs est commune et on peut donc utiliser les concepts de cosinus et sinus pour exprimer ces vecteurs en termes de longueur et d'angle autour de l'axe OX :





Notez que nous pouvons utiliser les formules somme et cosinus pour étendre les valeurs x ' et y' . Pour ceux qui ont oublié, je rappellerai ces formules:





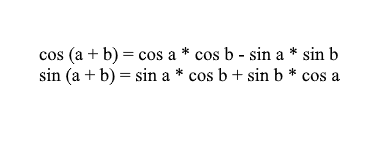
En développant les coordonnées du vecteur pivoté à travers eux, nous obtenons:





Il est facile de voir ici que les facteurs l * cos a et l * sin a sont les coordonnées du vecteur original: x = l * cos a, y = l * sin a . Remplaçons-les par x et y :





Ainsi, nous avons exprimé le vecteur tourné par les coordonnées du vecteur d'origine et l'angle de sa rotation. En tant que matrice, cette expression ressemblera à ceci:





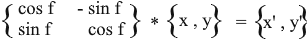
Multipliez et vérifiez que le résultat est équivalent à ce que nous en avons déduit.

Rotation dans l'espace 3D

Nous avons considéré la rotation dans un espace bidimensionnel et en avons également dérivé une matrice. Maintenant, la question se pose, comment obtenir de telles transformations pour trois dimensions? Dans le cas bidimensionnel, nous avons fait pivoter des vecteurs sur un plan, mais ici il y a un nombre infini de plans par rapport auxquels nous pouvons faire cela. Cependant, il existe trois types de rotation de base avec lesquels vous pouvez exprimer n'importe quelle rotation d'un vecteur dans un espace tridimensionnel - ce sont les rotations XY , XZ , YZ . Rotation



XY .



Avec cette rotation, nous faisons pivoter le vecteur autour de l'axe OZ du système de coordonnées. Imaginez que les vecteurs sont les pales de l'hélicoptère et que l'axe OZ est le mât auquel ils s'accrochent. Avec XYla rotation du vecteur tournera autour de l'axe OZ , comme les pales d'un hélicoptère par rapport au mât.





Notez qu'avec cette rotation, les coordonnées z des vecteurs ne changent pas, mais les coordonnées x et x changent - c'est pourquoi cela s'appelle la rotation XY .





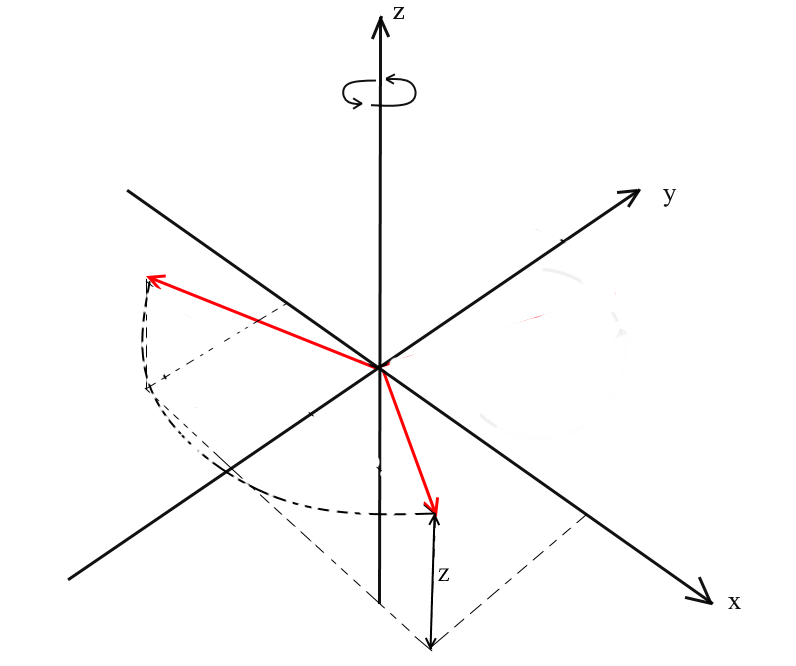
Il n'est pas difficile de dériver des formules pour une telle rotation: z - la coordonnée reste la même, et x et y changent selon les mêmes principes que dans la rotation 2D.





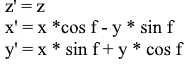
La même chose sous forme de matrice:





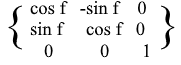
Pour les rotations XZ et YZ , tout est pareil:

Projection

Le concept de projection peut varier en fonction du contexte dans lequel il est utilisé. Beaucoup ont probablement entendu parler de concepts tels que la projection sur un plan ou la projection sur un axe de coordonnées.



Dans la compréhension que nous utilisons ici, la projection sur un vecteur est également un vecteur. Ses coordonnées sont le point d'intersection de la perpendiculaire est passé de vecteur a à b avec le vecteur b .





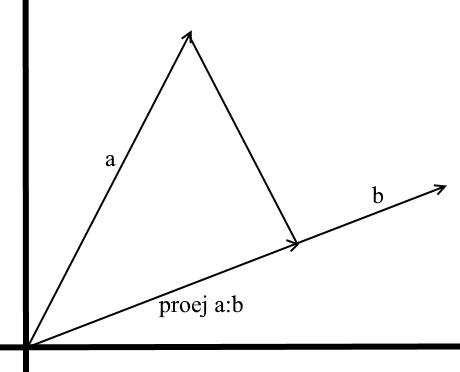
Pour définir un tel vecteur, nous devons connaître sa longueur et sa direction . Comme nous le savons, la jambe adjacente et l'hypoténuse dans un triangle rectangle sont liées par le rapport cosinus, nous l'utilisons donc pour exprimer la longueur du vecteur de projection:





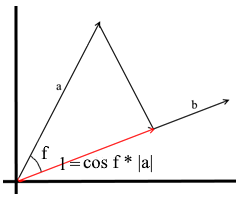
La direction du vecteur de projection coïncide par définition avec le vecteur b , ce qui signifie que la projection est déterminée par la formule:





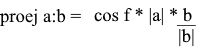
Ici, nous obtenons la direction de la projection en tant que vecteur unitaire et la multiplions par la longueur de la projection. Il n'est pas difficile de comprendre que le résultat sera exactement ce que nous recherchons.



Représentons maintenant tout en termes de produit scalaire :





Nous obtenons une formule pratique pour trouver la projection:

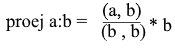
Systèmes de coordonnées. Bases

Beaucoup sont habitués à travailler dans le système de coordonnées XYZ standard , dans lequel 2 axes seront perpendiculaires l'un à l'autre, et les axes de coordonnées peuvent être représentés comme des vecteurs unitaires:





En fait, il existe une infinité de systèmes de coordonnées, chacun d'eux étant une base . La base de l'espace à n dimensions est un ensemble de vecteurs {v1, v2 …… vn} à travers lesquels tous les vecteurs de cet espace sont représentés. Dans ce cas, aucun vecteur de la base ne peut être représenté par ses autres vecteurs. En fait, chaque base est un système de coordonnées séparé dans lequel les vecteurs auront leurs propres coordonnées uniques.



Jetons un coup d'œil à ce qu'est la base de l'espace bidimensionnel. Prenons, par exemple, le système de coordonnées cartésien familier des vecteurs X {1, 0} , Y {0, 1} , qui est l'une des bases de l'espace bidimensionnel:







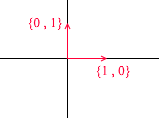
Tout vecteur sur un plan peut être représenté comme une somme de vecteurs de cette base avec certains coefficients, ou comme une combinaison linéaire . Souvenez-vous de ce que vous faites lorsque vous écrivez les coordonnées d'un vecteur - vous écrivez x - la coordonnée, puis - y . C'est ainsi que vous déterminez réellement les coefficients d'expansion en termes de vecteurs de base.







Prenons maintenant une autre base:







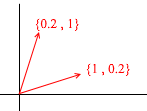
Tout vecteur 2D peut également être représenté par ses vecteurs:







Mais un tel ensemble de vecteurs n'est pas la base d'un espace à deux dimensions:







Dans celui-ci, deux vecteurs {1,1} et {2,2} se trouvent sur une ligne droite. Quelles que soient leurs combinaisons que vous prenez, vous ne recevrez que des vecteurs situés sur la droite commune y = x . Pour nos besoins, de tels défauts ne seront pas utiles, cependant, je pense qu'il vaut la peine de comprendre la différence. Par définition, toutes les bases sont unies par une propriété - aucun des vecteurs de base ne peut être représenté comme une somme d'autres vecteurs de base avec des coefficients, ou aucun des vecteurs de base n'est une combinaison linéaire des autres. Voici un exemple d'un ensemble de 3 vecteurs qui n'est pas non plus une base :







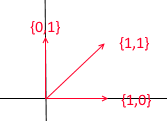
Tout vecteur d'un plan bidimensionnel peut être exprimé à travers lui , mais le vecteur {1, 1} qu'il contient est superflu, car il peut lui-même être exprimé par les vecteurs {1, 0} et {0,1} comme {1,0} + {0,1 } .



En général, toute base d'un espace à n dimensions contiendra exactement n vecteurs, pour 2e ce n est respectivement égal à 2.



Tournons-nous vers 3d. La base tridimensionnelle contiendra 3 vecteurs:







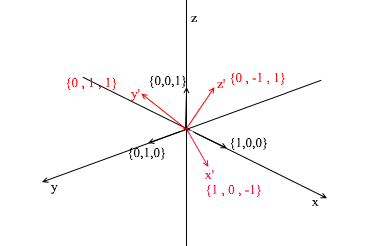
Si pour une base bidimensionnelle il suffisait de deux vecteurs ne reposant pas sur une ligne droite, alors dans un espace tridimensionnel un ensemble de vecteurs sera une base si:

• 1) 2 vecteurs ne se trouvent pas sur une ligne droite
• 2) le troisième ne repose pas sur le plan formé par les deux autres.

Désormais, les bases avec lesquelles nous travaillons seront orthogonales (n'importe lequel de leurs vecteurs est perpendiculaire) et normalisées (la longueur de tout vecteur de base est 1). Nous n'aurons tout simplement pas besoin des autres. Par exemple, la base standard







répond à ces critères.

Transition vers une autre base

Jusqu'à présent, nous avons écrit la décomposition d'un vecteur comme une somme de vecteurs de base avec des coefficients:





Considérons à nouveau la base standard - le vecteur {1, 3, 6} qu'il contient peut s'écrire comme suit:





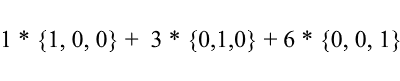
Comme vous pouvez le voir, les coefficients d'expansion d'un vecteur dans la base sont ses coordonnées dans cette base . Regardons l'exemple suivant:







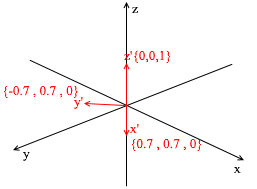
Cette base est dérivée de la norme en lui appliquant une rotation XY de 45 degrés. Prenez un vecteur a dans le système standard avec les coordonnées {0, 1, 1}







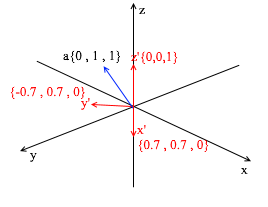
Grâce aux vecteurs de la nouvelle base, elle peut être développée comme suit:







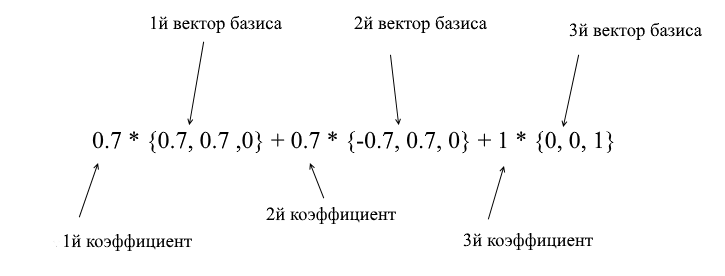
Si vous calculez ce montant, vous obtiendrez {0, 1, 1} - le vecteur a dans la base standard. Sur la base de cette expression dans la nouvelle base, le vecteur a a des coordonnées {0,7, 0,7, 1} - les coefficients d'expansion. Ce sera plus visible si vous regardez sous un angle différent:







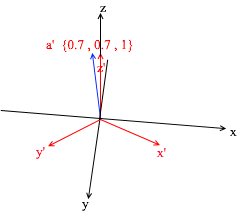
Mais comment trouvez-vous ces coefficients? En général, une méthode universelle est la solution d'un système assez complexe d'équations linéaires. Cependant, comme je l'ai dit plus tôt, nous n'utiliserons que des bases orthogonales et normalisées , et pour elles, il existe un moyen très triche. Il consiste à trouver des projections sur les vecteurs de base. Utilisons-le pour trouver la décomposition du vecteur a dans la base X {0.7, 0.7, 0} Y {-0.7, 0.7, 0} Z {0, 0, 1}







Tout d'abord, trouvons le coefficient pour y ' . La première étape consiste à trouver la projection du vecteur a sur le vecteur y ' (j'ai expliqué comment faire cela ci-dessus):







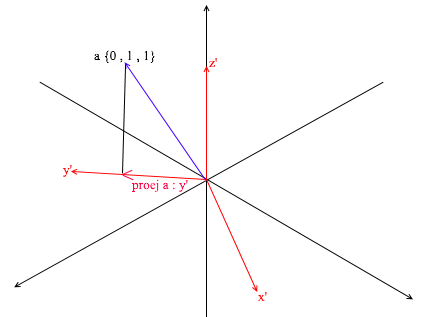
La deuxième étape: nous divisons la longueur de la projection trouvée par la longueur du vecteur y ' , nous découvrons ainsi «combien de vecteurs y' rentrent dans le vecteur de projection» - ce nombre sera le coefficient pour y ' , et aussi y - la coordonnée du vecteur a dans la nouvelle base! Pour x ' et z', répétez des opérations similaires:







Nous avons maintenant des formules pour le passage d'une base standard à une nouvelle:







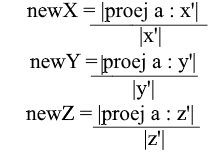
Eh bien, puisque nous n'utilisons que des bases normalisées et que les longueurs de leurs vecteurs sont égales à 1, il n'est pas nécessaire de diviser par la longueur du vecteur dans la formule de transition:







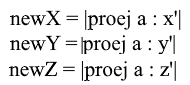
Développez la coordonnée x via la formule de projection:







Notez que le dénominateur (x ', x') et le vecteur x ' dans le cas d'une base normalisée sont également égaux à 1 et peuvent être ignorés. On a:







Nous voyons que la coordonnée x dans la base est exprimée comme le produit scalaire (a, x ') , la coordonnée y, respectivement, comme (a, y') , la coordonnée z est (a, z ') . Vous pouvez maintenant créer une matrice de transition vers de nouvelles coordonnées:

Systèmes de coordonnées décalés

Tous les systèmes de coordonnées que nous avons considérés ci-dessus avaient l'origine du point {0,0,0} . De plus, il existe également des systèmes avec un point d'origine décalé:







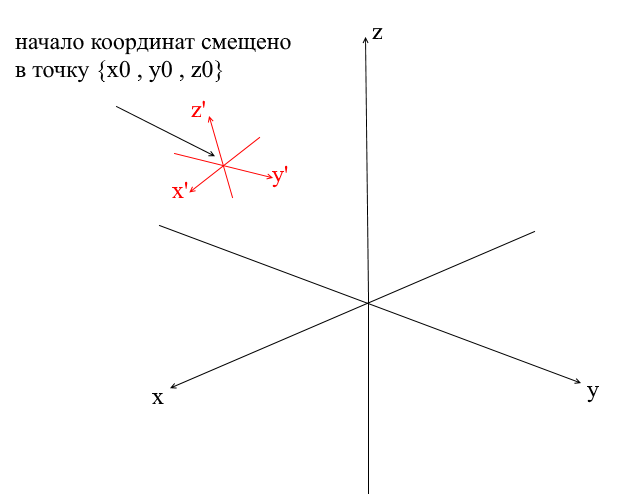
Afin de traduire un vecteur dans un tel système, vous devez d'abord l'exprimer par rapport au nouveau centre de coordonnées. Pour ce faire, c'est simple - soustrayez ce centre du vecteur. Ainsi, vous "déplacez" en quelque sorte le système de coordonnées lui-même vers un nouveau centre, tandis que le vecteur reste en place. Ensuite, vous pouvez utiliser la matrice de transition qui nous est déjà familière.

Ecrire un moteur de géométrie. Créez un rendu filaire.

Eh bien, je pense que quelqu'un qui a parcouru la section avec les mathématiques et n'a pas fermé l'article peut subir un lavage de cerveau avec des choses plus intéressantes! Dans cette section, nous allons commencer à écrire les bases d'un moteur 3D et du rendu. En général, le rendu est une procédure assez complexe qui comprend de nombreuses opérations différentes: découpage d'arêtes invisibles, pixellisation, calcul de la lumière, traitement de divers effets, matériaux (parfois même physiques). Nous analyserons partiellement tout cela à l'avenir, mais maintenant nous allons faire des choses plus simples - nous allons écrire un rendu filaire . Son essence est qu'il dessine un objet sous la forme de lignes reliant ses sommets, le résultat ressemble donc à un réseau de fils:

Graphiques polygonaux

Traditionnellement, l'infographie utilise des représentations polygonales de données d'objets 3D. Ainsi, les données sont présentées dans OBJ, 3DS, FBX et bien d'autres. Dans un ordinateur, ces données sont stockées sous la forme de deux ensembles: un ensemble de sommets et un ensemble de faces (polygones). Chaque sommet d'un objet est représenté par sa position dans l'espace - un vecteur, et chaque face (polygone) est représentée par trois entiers qui sont des indices des sommets de cet objet. Les objets les plus simples (cubes, sphères, etc.) sont constitués de tels polygones et sont appelés primitives.



Dans notre moteur, la primitive sera l'objet principal de la géométrie 3D - tous les autres objets en hériteront. Décrivons la classe de la primitive:

    abstract class Primitive
    {
        public Vector3[] Vertices { get; protected set; }
        public int[] Indexes { get; protected set; }
    }

Jusqu'à présent, tout est simple - il y a des sommets de la primitive et il y a des indices pour former des polygones. Vous pouvez maintenant utiliser cette classe pour créer un cube:

   public class Cube : Primitive
      {
        public Cube(Vector3 center, float sideLen)
        {
            var d = sideLen / 2;
            Vertices = new Vector3[]
                {
                    new Vector3(center.X - d , center.Y - d, center.Z - d) ,
                    new Vector3(center.X - d , center.Y - d, center.Z) ,
                    new Vector3(center.X - d , center.Y , center.Z - d) ,
                    new Vector3(center.X - d , center.Y , center.Z) ,
                    new Vector3(center.X + d , center.Y - d, center.Z - d) ,
                    new Vector3(center.X + d , center.Y - d, center.Z) ,
                    new Vector3(center.X + d , center.Y + d, center.Z - d) ,
                    new Vector3(center.X + d , center.Y + d, center.Z + d) ,
                };

            Indexes = new int[]
                {
                    1,2,4 ,
                    1,3,4 ,
                    1,2,6 ,
                    1,5,6 ,
                    5,6,8 ,
                    5,7,8 ,
                    8,4,3 ,
                    8,7,3 ,
                    4,2,8 ,
                    2,8,6 ,
                    3,1,7 ,
                    1,7,5
                };
        }
    }

int Main()
{
        var cube = new Cube(new Vector3(0, 0, 0), 2);
}

Implémentation de systèmes de coordonnées

Il ne suffit pas de définir un objet avec un ensemble de polygones; pour planifier et créer des scènes complexes, vous devez placer des objets à différents endroits, les faire pivoter, les réduire ou les augmenter en taille. Pour la commodité de ces opérations, les systèmes de coordonnées dits locaux et globaux sont utilisés. Chaque objet de la scène a son propre système de coordonnées - local, ainsi que son propre point central.





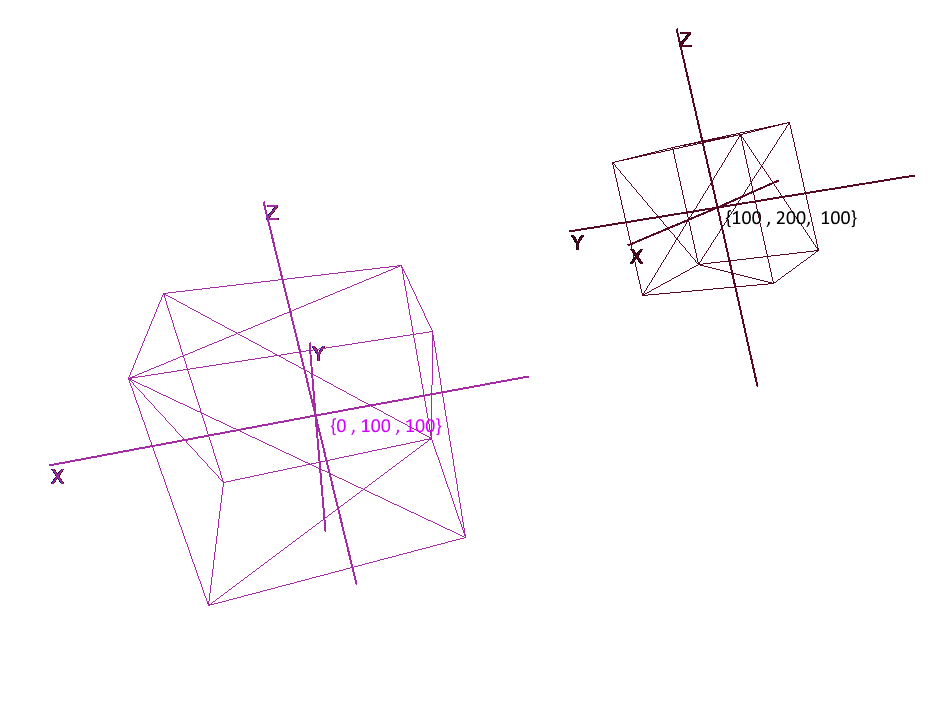
La représentation d'un objet en coordonnées locales vous permet d'effectuer facilement toutes les opérations avec lui. Par exemple, pour déplacer un objet par le vecteur a , il suffira de décaler le centre de son repère de ce vecteur, pour faire pivoter un objet - faire pivoter ses coordonnées locales.



Lorsque vous travaillez avec un objet, nous allons effectuer des opérations avec ses sommets dans le système de coordonnées local; lors du rendu, nous allons d'abord traduire tous les objets de la scène en un seul système de coordonnées - le système global. Ajoutons des systèmes de coordonnées au code. Pour ce faire, créez un objet de la classe Pivot (pivot, pivot point), qui représentera la base locale de l'objet et son point central. La conversion d'un point en système de coordonnées fourni par Pivot se fera en 2 étapes:

• 1) Représentation d'un point par rapport au centre de nouvelles coordonnées
• 2) Expansion en vecteurs de la nouvelle base

Au contraire, pour représenter le sommet local d'un objet en coordonnées globales, vous devez effectuer ces actions dans l'ordre inverse:

• 1) Expansion en vecteurs de la base globale
• 2) Représentation par rapport au centre global

Écrivons une classe pour représenter les systèmes de coordonnées:

    public class Pivot
    {
        // 
        public Vector3 Center { get; private set; }
        //   -   
        public Vector3 XAxis { get; private set; }
        public Vector3 YAxis { get; private set; }
        public Vector3 ZAxis { get; private set; }

        //    
        public Matrix3x3 LocalCoordsMatrix => new Matrix3x3
            (
                XAxis.X, YAxis.X, ZAxis.X,
                XAxis.Y, YAxis.Y, ZAxis.Y,
                XAxis.Z, YAxis.Z, ZAxis.Z
            );

        //    
        public Matrix3x3 GlobalCoordsMatrix => new Matrix3x3
            (
                XAxis.X , XAxis.Y , XAxis.Z,
                YAxis.X , YAxis.Y , YAxis.Z,
                ZAxis.X , ZAxis.Y , ZAxis.Z
            );

        public Vector3 ToLocalCoords(Vector3 global)
        {
            //          
            return LocalCoordsMatrix * (global - Center);
        }
        public Vector3 ToGlobalCoords(Vector3 local)
        {
            //    -            
            return (GlobalCoordsMatrix * local)  + Center;
        }

        public void Move(Vector3 v)
        {
            Center += v;
        }

        public void Rotate(float angle, Axis axis)
        {
            XAxis = XAxis.Rotate(angle, axis);
            YAxis = YAxis.Rotate(angle, axis);
            ZAxis = ZAxis.Rotate(angle, axis);
        }
    }

Maintenant, en utilisant cette classe, ajoutez les fonctions de rotation, de mouvement et d'augmentation aux primitives:

    public abstract class Primitive
    {
        //  
        public Pivot Pivot { get; protected set; }
        // 
        public Vector3[] LocalVertices { get; protected set; }
        // 
        public Vector3[] GlobalVertices { get; protected set; }
        // 
        public int[] Indexes { get; protected set; }

        public void Move(Vector3 v)
        {
            Pivot.Move(v);

            for (int i = 0; i < LocalVertices.Length; i++)
                GlobalVertices[i] += v;
        }

        public void Rotate(float angle, Axis axis)
        {
            Pivot.Rotate(angle , axis);

            for (int i = 0; i < LocalVertices.Length; i++)
                GlobalVertices[i] = Pivot.ToGlobalCoords(LocalVertices[i]);
        }

        public void Scale(float k)
        {
            for (int i = 0; i < LocalVertices.Length; i++)
                LocalVertices[i] *= k;

            for (int i = 0; i < LocalVertices.Length; i++)
                GlobalVertices[i] = Pivot.ToGlobalCoords(LocalVertices[i]);
        }
    }

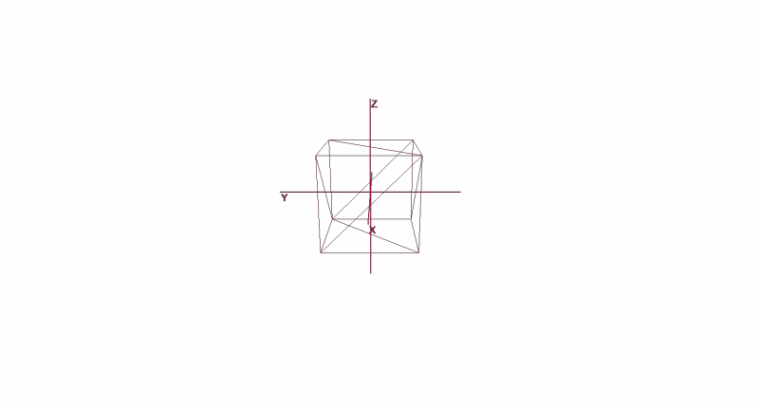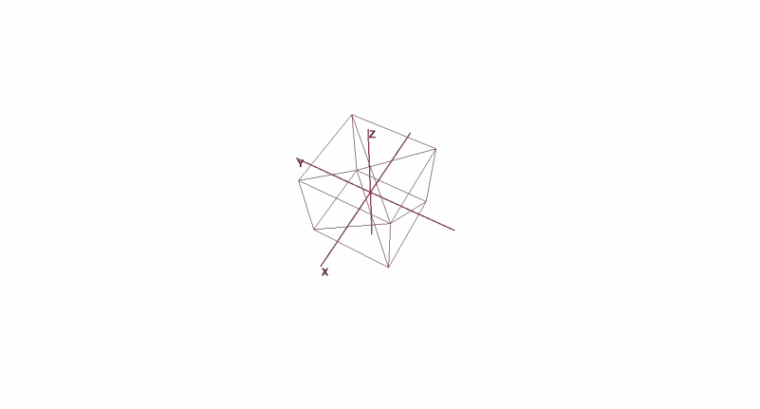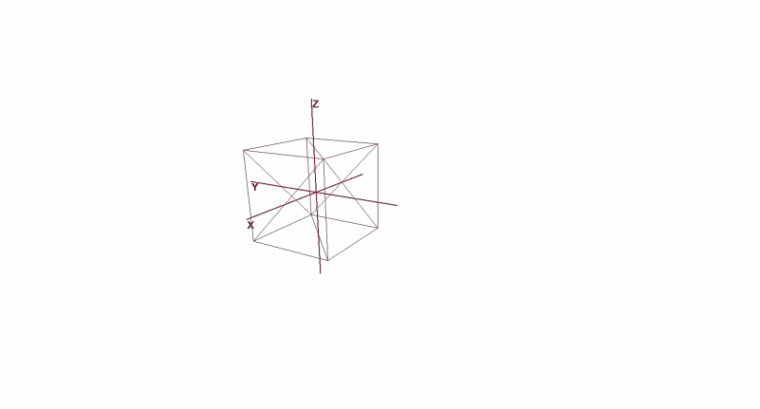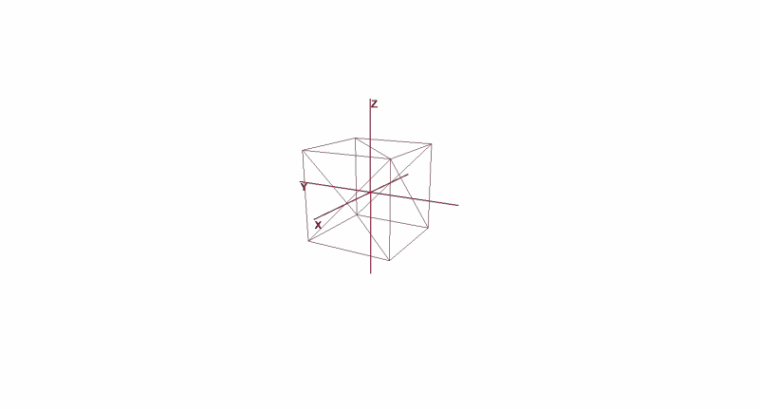
Rotation et déplacement d'un objet à l'aide de coordonnées locales

Dessin de polygones. Caméra

L'objet principal de la scène sera la caméra - avec son aide, les objets seront dessinés sur l'écran. La caméra, comme tous les objets de la scène, aura des coordonnées locales sous la forme d'un objet de la classe Pivot - à travers elle, nous déplacerons et ferons pivoter la caméra:





Pour afficher l'objet à l'écran, nous utiliserons une méthode de projection en perspective simple . Le principe sur lequel repose cette méthode est que plus l'objet est éloigné de nous, plus il paraîtra petit . Probablement beaucoup ont résolu une fois à l'école le problème de la mesure de la hauteur d'un arbre à une certaine distance de l'observateur:





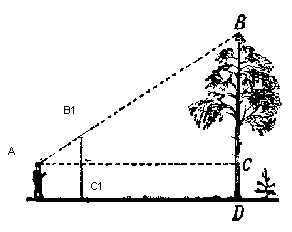
Imaginons qu'un rayon du point haut d'un arbre tombe sur un certain plan de projection situé à une distance C1 de l'observateur et dessine un point dessus. L'observateur voit ce point et veut en déterminer la hauteur de l'arbre. Comme vous pouvez le voir, la hauteur de l'arbre et la hauteur d'un point sur le plan de projection sont liées par le rapport de triangles similaires. Ensuite, l'observateur peut déterminer la hauteur du point en utilisant ce rapport:







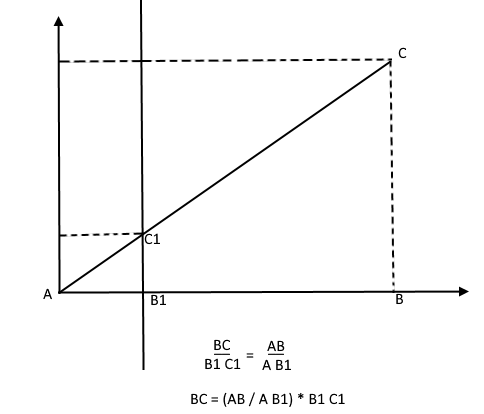
Au contraire, connaissant la hauteur de l'arbre, il peut trouver la hauteur d'un point sur le plan de projection:







Revenons maintenant à notre caméra. Imaginons que un plan de projection est fixé à l' z- axe de la caméra à une distance z ' à partir de l'origine. La formule pour un tel plan est z = z ' , elle peut être donnée par un nombre - z' . Les rayons des sommets de divers objets tombent sur ce plan. Lorsque le rayon atteint l'avion, il laissera un point dessus. En connectant ces points, vous pouvez dessiner un objet.







Ce plan représentera l'écran. Nous trouverons la coordonnée de la projection du sommet de l'objet sur l'écran en 2 étapes:

• 1) Nous traduisons le sommet en coordonnées locales de la caméra
• 2) Trouvez la projection d'un point par le rapport de triangles similaires

La projection sera un vecteur à 2 dimensions, ses coordonnées x 'et y' définiront la position du point sur l'écran de l'ordinateur.





Ce code comporte plusieurs erreurs, dont nous parlerons plus tard.

Couper les polygones invisibles

Après avoir projeté trois points du polygone sur l'écran de cette manière, nous obtenons les coordonnées du triangle qui correspond à l'affichage du polygone sur l'écran. Mais de cette manière, la caméra traitera tous les sommets, y compris ceux dont les projections vont au-delà de la zone de l'écran, si vous essayez de dessiner un tel sommet, il y a une forte probabilité d'attraper des erreurs. La caméra traitera également les polygones qui se trouvent derrière (les coordonnées z de leurs points dans la ligne de base de la caméra locale sont inférieures à z ' ) - nous n'avons pas non plus besoin d'une telle vision "occipitale".







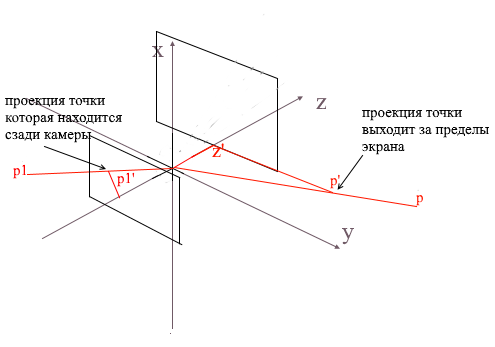
Pour découper des sommets invisibles dans open gl, la méthode de la pyramide de troncature est utilisée. Il consiste à définir deux plans - proche (plan proche) et éloigné (plan éloigné). Tout ce qui se trouve entre ces deux plans fera l'objet d'un traitement ultérieur. J'utilise une version simplifiée avec un plan de détourage - z ' . Tous les sommets derrière seront invisibles.



Ajoutons deux nouveaux champs à la caméra: la largeur et la hauteur de l'écran.

Maintenant, chaque point projeté sera vérifié pour toucher la zone de l'écran. Coupons également les points derrière la caméra. Si le point se trouve derrière ou que sa projection ne tombe pas sur l'écran, alors la méthode renverra le point {float.NaN, float.NaN} .

Traduire en coordonnées d'écran

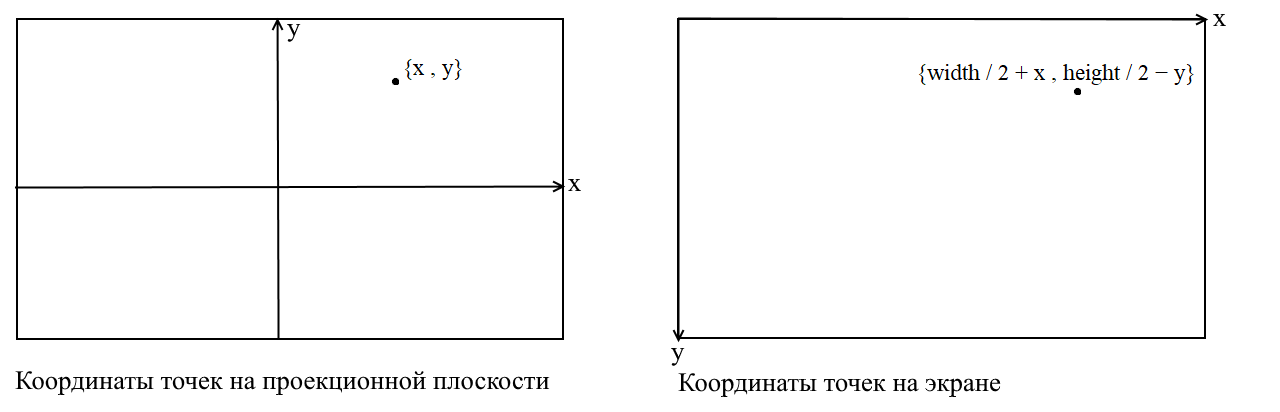
Ici, je vais clarifier un point. Cela est lié au fait que dans de nombreuses bibliothèques graphiques, le dessin a lieu dans le système de coordonnées de l'écran, dans de telles coordonnées, l'origine est le point supérieur gauche de l'écran, x augmente lors du déplacement vers la droite et y lors du déplacement vers le bas. Dans notre plan de projection, les points sont représentés en coordonnées cartésiennes ordinaires , et avant le dessin, ces coordonnées doivent être converties en coordonnées d'écran. C'est facile à faire, il vous suffit de déplacer l'origine vers le coin supérieur gauche et d'inverser y :

Ajustement de la taille de l'image projetée

Si vous utilisez le code précédent pour dessiner un objet, vous obtiendrez quelque chose comme ceci:







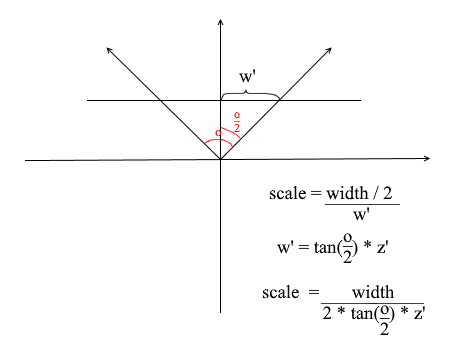
Pour une raison quelconque, tous les objets sont dessinés très petits. Afin de comprendre la raison, rappelez-vous comment nous avons calculé la projection - nous avons multiplié les coordonnées x et y par le delta du rapport z '/ z . Cela signifie que la taille de l'objet sur l'écran dépend de la distance au plan de projection z ' . Mais nous pouvons définir z ' aussi petit que nous le voulons. Cela signifie que nous devons ajuster la taille de la projection en fonction de la valeur z ' actuelle . Pour ce faire, ajoutons un autre champ à la caméra - son angle de vue .







Nous en avons besoin pour faire correspondre la taille angulaire de l' écran à sa largeur. L'angle sera adapté à la largeur de l'écran de cette manière: l' angle maximum dans lequel la caméra regarde est le bord gauche ou droit de l'écran. L'angle maximum par rapport à l'axe z de la caméra est alors o / 2 . La projection qui a frappé le bord droit de l'écran doit avoir la coordonnée x = largeur / 2 et celle de gauche: x = -width / 2 . Sachant cela, nous dérivons la formule pour trouver le coefficient d'étirement de projection:









Voici un code de rendu simple que j'ai utilisé pour le test:





Vérifions le rendu sur la scène et les cubes:







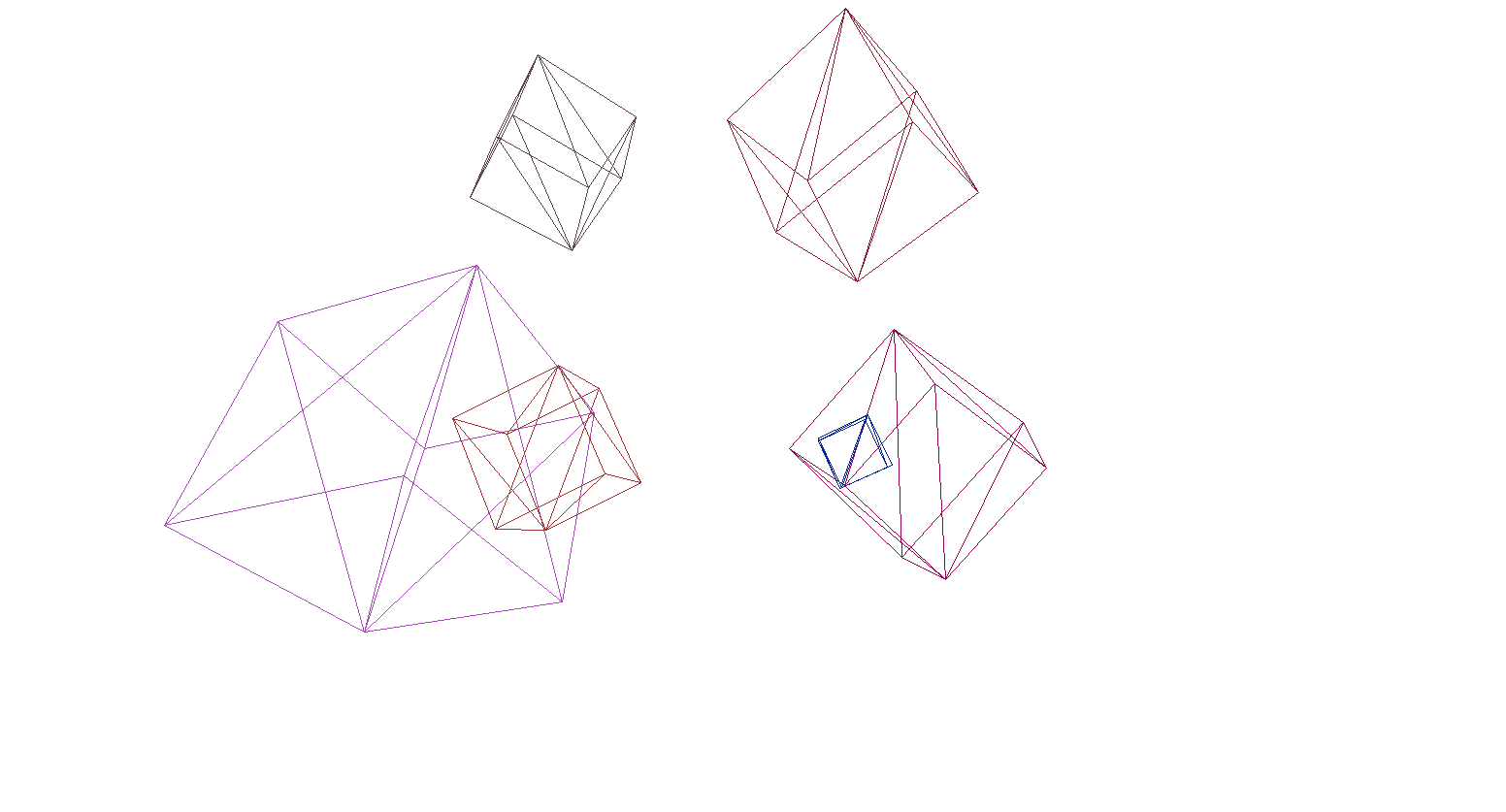
Et oui, tout fonctionne très bien. Pour ceux qui ne trouvent pas les cubes colorés prétentieux, j'ai écrit une fonction pour analyser les modèles au format OBJ en objets primitifs, rempli l'arrière-plan de noir et rendu plusieurs modèles:

Rastérisation des polygones. Nous apportons de la beauté.

Dans la dernière section, nous avons écrit un rendu filaire. Nous allons maintenant nous occuper de sa modernisation - nous allons mettre en œuvre la rastérisation des polygones. Rastériser



simplement un polygone signifie le peindre. Il semblerait pourquoi écrire un vélo alors qu'il existe déjà des fonctions de tramage de triangle prêtes à l'emploi. Voici ce qui se passe si vous dessinez tout avec les outils par défaut:







De l'art contemporain, des polygones derrière les frontaux ont été dessinés, en un mot - du porridge. Aussi, comment texturez-vous les objets de cette manière? Oui, pas moyen. Nous devons donc écrire notre propre imba-rasterizer, qui pourra couper les points invisibles , les textures et même les shaders! Mais pour ce faire, il vaut la peine de comprendre comment peindre des triangles en général.

Algorithme de Bresenham pour le dessin au trait.

Commençons par les lignes. Si quelqu'un ne connaissait pas l'algorithme de Bresenham, c'est l'algorithme principal pour dessiner des lignes droites en infographie. Il ou ses modifications sont utilisés littéralement partout: dessiner des lignes, des segments, des cercles, etc. Qui est intéressé par une description plus détaillée - lisez le wiki. Algorithme de Bresenham



Il existe un segment de droite reliant les points {x1, y1} et {x2, y2} . Pour dessiner un segment entre eux, vous devez peindre sur tous les pixels qui tombent dessus. Pour deux points du segment, vous pouvez trouver les coordonnées x des pixels dans lesquels ils se trouvent: il vous suffit de prendre des parties entières des coordonnées x1 et x2 . Pour peindre les pixels sur le segment, on commence le cycle de x1 à x2 et à chaque itération on calculey - coordonnée du pixel qui tombe sur la ligne. Voici le code:

void Brezenkhem(Vector2 p1 , Vector2 p2)
{
    int x1 = Floor(p1.X);
    int x2 = Floor(p2.X);
    if (x1 > x2) {Swap(x1, x2); Swap(p1 , p2);}
    float d = (p2.Y - p1.Y) / (x2 - x1);
    float y = p1.Y;
    for (int i = x1; i <= x2; i++)
    {
        int pixelY = Floor(y);
        FillPixel(i , pixelY);
        y += d;
    }
}

Image du wiki

Rastérisez un triangle. Algorithme de remplissage

On sait dessiner des lignes, mais avec des triangles ce sera un peu plus difficile (pas beaucoup)! La tâche de dessiner un triangle est réduite à plusieurs tâches de dessin de lignes. Commençons par diviser le triangle en deux parties, après avoir préalablement trié les points dans l'ordre croissant x :







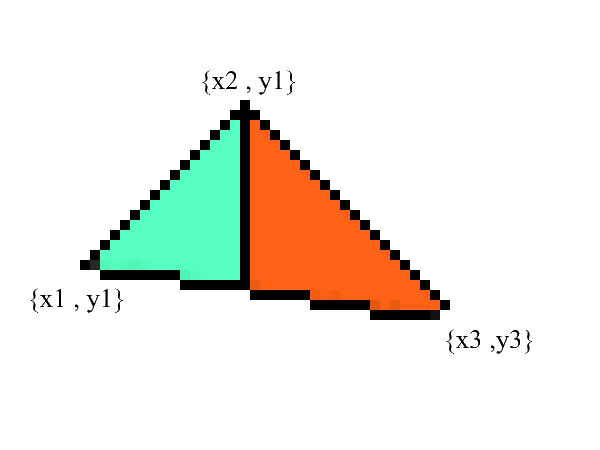
Remarquez - nous avons maintenant deux parties dans lesquelles les bordures inférieure et supérieure sont clairement exprimées . il ne reste plus qu'à remplir tous les pixels intermédiaires! Cela peut être fait en 2 cycles: de x1 à x2 et de x3 à x2 .

void Triangle(Vector2 v1 , Vector2 v2 , Vector2 v3)
{
    // BubbleSort    x
    if (v1.X > v2.X) { Swap(v1, v2); }
    if (v2.X > v3.X) { Swap(v2, v3); }
    if (v1.X > v2.X) { Swap(v1, v2); }

    //    y    x
    //   0:  x1 == x2     - 
    var steps12 = max(v2.X - v1.X , 1);
    var steps13 = max(v3.X - v1.X , 1);
    var upDelta = (v2.Y - v1.Y) / steps12;
    var downDelta = (v3.Y - v1.Y) / steps13;

    //     
    if (upDelta < downDelta) Swap(upDelta , downDelta);

    //     y1
    var up = v1.Y;
    var down = v1.Y;

    for (int i = (int)v1.X; i <= (int)v2.X; i++)
    {
        for (int g = (int)down; g <= (int)up; g++)
        {
            FillPixel(i , g);
        }
        up += upDelta;
        down += downDelta;
    }

    //       
    var steps32 = max(v2.X - v3.X , 1);
    var steps31 = max(v1.X - v3.X , 1);
    upDelta = (v2.Y - v3.Y) / steps32;
    downDelta = (v1.Y - v3.Y) / steps31;

    if (upDelta < downDelta) Swap(upDelta, downDelta);

    up = v3.Y;
    down = v3.Y;

    for (int i = (int)v3.X; i >=(int)v2.X; i--)
    {
        for (int g = (int)down; g <= (int)up; g++)
        {
            FillPixel(i, g);
        }
        up += upDelta;
        down += downDelta;
    }
}

Sans aucun doute, ce code peut être refactorisé et ne pas dupliquer la boucle:

void Triangle(Vector2 v1 , Vector2 v2 , Vector2 v3)
{
    if (v1.X > v2.X) { Swap(v1, v2); }
    if (v2.X > v3.X) { Swap(v2, v3); }
    if (v1.X > v2.X) { Swap(v1, v2); }

    var steps12 = max(v2.X - v1.X , 1);
    var steps13 = max(v3.X - v1.X , 1);
    var steps32 = max(v2.X - v3.X , 1);
    var steps31 = max(v1.X - v3.X , 1);

    var upDelta = (v2.Y - v1.Y) / steps12;
    var downDelta = (v3.Y - v1.Y) / steps13;
    if (upDelta < downDelta) Swap(upDelta , downDelta);

    TrianglePart(v1.X , v2.X , v1.Y , upDelta , downDelta);

    upDelta = (v2.Y - v3.Y) / steps32;
    downDelta = (v1.Y - v3.Y) / steps31;
    if (upDelta < downDelta) Swap(upDelta, downDelta);

    TrianglePart(v3.X, v2.X, v3.Y, upDelta, downDelta);
}

void TrianglePart(float x1 , float x2 , float y1  , float upDelta , float downDelta)
{
    float up = y1, down = y1;
    for (int i = (int)x1; i <= (int)x2; i++)
    {
        for (int g = (int)down; g <= (int)up; g++)
        {
            FillPixel(i , g);
        }
        up += upDelta; down += downDelta;
    }
}

Coupure des points invisibles.

Tout d'abord, pensez à la façon dont vous voyez. Maintenant, il y a un écran devant vous, et ce qu'il y a derrière est caché à vos yeux. Dans le rendu, un mécanisme similaire fonctionne - si un polygone en chevauche un autre, le rendu le dessinera sur celui superposé. Au contraire, il ne dessinera pas la partie fermée du polygone:







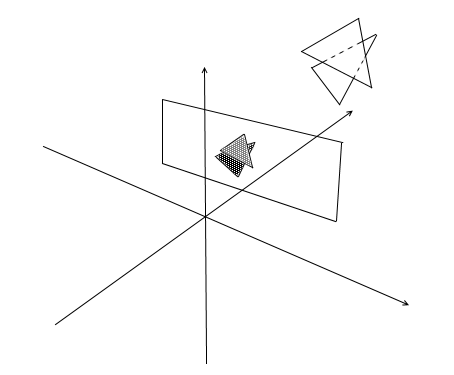
Afin de comprendre si les points sont visibles ou non, le mécanisme zbuffer (tampon de profondeur) est utilisé dans le rendu . zbuffer peut être considéré comme un tableau bidimensionnel (peut être compressé en unidimensionnel) avec largeur * hauteur . Pour chaque pixel à l'écran, il stocke une valeur z - les coordonnées du polygone d'origine à partir duquel ce point a été projeté. En conséquence, plus le point est proche de l'observateur, plus sa coordonnée z est petite . En fin de compte, si les projections de plusieurs points coïncident, vous devez pixelliser le point avec la coordonnée z minimale :







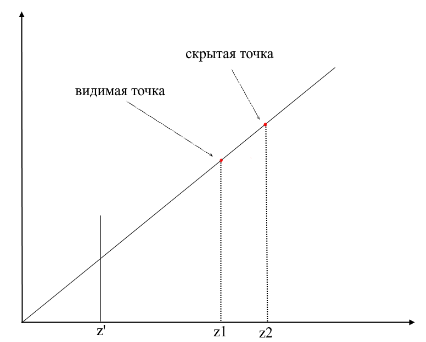
Maintenant, la question se pose - comment trouver les coordonnées z des points sur le polygone d'origine? Cela peut être fait de plusieurs manières. Par exemple, vous pouvez tirer un rayon depuis l'origine de la caméra, en passant par un point du plan de projection {x, y, z '} et trouver son intersection avec le polygone. Mais la recherche d'intersections est une opération extrêmement coûteuse, nous utiliserons donc une méthode différente. Pour dessiner un triangle, nous avons interpolé les coordonnées de ses projections , maintenant, en plus de cela, nous allons également interpoler les coordonnées du polygone d'origine . Pour couper les points invisibles, nous utiliserons l'état zbuffer pour l'image courante dans la méthode de rastérisation .



Mon zbuffer ressemblera àVector3 [] - il contiendra non seulement les coordonnées z , mais aussi les valeurs interpolées des points de polygone (fragments) pour chaque pixel de l'écran. Ceci est fait afin d'économiser de la mémoire, car à l'avenir, nous aurons encore besoin de ces valeurs pour écrire des shaders ! En attendant, nous avons le code suivant pour déterminer les sommets visibles (fragments) :







Animation des étapes du rasterizer (lors de la réécriture de la profondeur dans zbuffer, le pixel est surligné en rouge):



Pour plus de commodité, j'ai déplacé tout le code dans un module Rasterizer séparé:





Maintenant, vérifions le travail de rendu. Pour cela j'utilise le modèle de Sylvanas du célèbre RPG "WOW":







Pas très clair, non? C'est parce qu'il n'y a pas de textures ou d'éclairage ici. Mais nous allons le réparer bientôt.

Textures! Ordinaire! Éclairage! Moteur!

Pourquoi ai-je tout combiné en une seule section? Et parce que par essence la texturation et le calcul des normales sont absolument identiques et vous le comprendrez bientôt.



Tout d'abord, regardons la tâche de texturation pour un polygone. Maintenant, en plus des coordonnées habituelles des sommets du polygone, nous allons également stocker ses coordonnées de texture . La coordonnée de texture du sommet est représentée sous la forme d'un vecteur 2D et pointe vers un pixel dans l'image de texture. J'ai trouvé une bonne image sur Internet pour montrer ceci:





Notez que le début de la texture ( pixel en bas à gauche ) dans les coordonnées de texture est {0, 0} , et la fin ( pixel en haut à droite ) est {1, 1} . Tenez compte du système de coordonnées de texture et de la possibilité d'aller au-delà des frontières de l'image lorsque la coordonnée de texture est 1.



Créons une classe pour représenter tout de suite les données des sommets:

  public class Vertex
    {
        public Vector3 Position { get; set; }
        public Color Color { get; set; }
        public Vector2 TextureCoord { get; set; }
        public Vector3 Normal { get; set; }

        public Vertex(Vector3 pos , Color color , Vector2 texCoord , Vector3 normal)
        {
            Position = pos;
            Color = color;
            TextureCoord = texCoord;
            Normal = normal;
        }
    }

J'expliquerai pourquoi les normales sont nécessaires plus tard, pour l'instant nous saurons simplement que les sommets peuvent les avoir. Maintenant, pour texturer le polygone, nous devons en quelque sorte mapper la valeur de couleur de la texture à un pixel spécifique. Rappelez-vous comment nous avons interpolé les sommets? Faites la même chose ici! Je ne réécrirai pas le code de rastérisation à nouveau, mais je vous suggère d'implémenter vous-même la texturation dans votre rendu. Le résultat doit être l'affichage correct des textures sur le modèle. Voici ce que j'ai:







Toutes les informations sur les coordonnées de texture du modèle se trouvent dans le fichier OBJ. Pour l'utiliser, apprenez le format: Format OBJ.

Éclairage

Avec les textures, tout est devenu beaucoup plus amusant, mais le vrai plaisir sera lorsque nous mettrons en œuvre l'éclairage de la scène. Pour simuler un éclairage "bon marché", j'utiliserai le modèle Phong .

Modèle Phong

En général, cette méthode simule la présence de 3 composants d'éclairage: le fond (ambiante), dispersé (diffus) et le miroir (reflet). La somme de ces trois composants simulera éventuellement le comportement physique de la lumière.





Modèle Phong



Pour calculer l'éclairage Phong, nous avons besoin de normales de surface, pour cela je les ai ajoutées dans la classe Vertex. Où pouvons-nous trouver les valeurs de ces normales? Non, nous n'avons rien à calculer. Le fait est que les éditeurs 3D généreux les considèrent souvent eux-mêmes et fournissent des modèles avec les données dans le contexte du format OBJ. Après avoir analysé le fichier modèle, nous obtenons la valeur normale pour 3 sommets de chaque polygone.





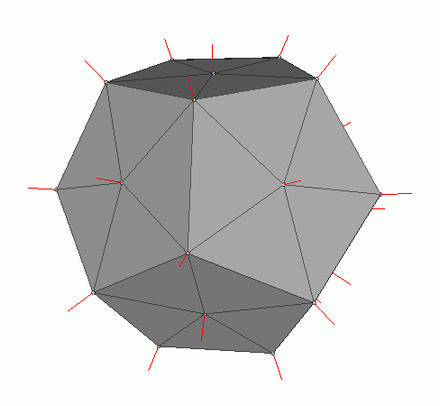
Image du wiki



Afin de calculer la normale à chaque point du polygone, vous devez interpoler ces valeurs, nous savons déjà comment faire cela. Jetons maintenant un coup d'œil à tous les composants pour calculer l'éclairage Phong.

Lumière d'arrière-plan (ambiante)

Initialement, nous définissons l' éclairage de fond constant , pour les objets non texturés, vous pouvez choisir n'importe quelle couleur pour les objets avec des textures Je divise chacun des composants RVB selon un rapport d'ombrage de base (baseShading).

Lumière diffuse

Lorsque la lumière atteint la surface du polygone, elle est uniformément dispersée. Pour calculer la valeur diffuse à un pixel spécifique, l' angle auquel la lumière atteint la surface est pris en compte . Pour calculer cet angle, vous pouvez appliquer le produit scalaire du rayon incident et de la normale (bien sûr, les vecteurs doivent être normalisés avant cela). Cet angle sera multiplié par un facteur d'intensité lumineuse. Si le produit scalaire est négatif, cela signifie que l'angle entre les vecteurs est supérieur à 90 degrés. Dans ce cas, nous commencerons à calculer non pas un éclaircissement, mais, au contraire, un ombrage. Cela vaut la peine d'éviter ce point, vous pouvez le faire en utilisant la fonction max .





Appliquons une lumière diffuse et dissipons l'obscurité:

Miroir lumière (Reflect)

Pour calculer le composant miroir, vous devez prendre en compte le point à partir duquel nous regardons l'objet . Nous allons maintenant prendre le produit scalaire du rayon de l'observateur et du rayon réfléchi par la surface multiplié par le facteur d'intensité lumineuse.





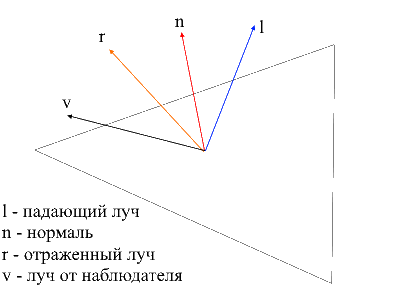
Il est facile de trouver le rayon de l'observateur à la surface - ce sera simplement la position du sommet traité en coordonnées locales . Afin de trouver le rayon réfléchi, j'ai utilisé la méthode suivante. Le rayon incident peut être décomposé en 2 vecteurs: sa projection sur la normale et le deuxième vecteur, que l'on peut trouver en soustrayant cette projection au rayon incident. Pour trouver le rayon réfléchi, vous devez soustraire la valeur du deuxième vecteur de la projection à la normale.





Maintenant, l'image ressemble à ceci:

Ombres

Le point final de ma présentation sera la mise en œuvre des ombres pour le rendu. La première idée sans issue qui est née dans mon crâne est de vérifier pour chaque point s'il y a un polygone entre lui et la lumière . Si c'est le cas, vous n'avez pas besoin d'éclairer le pixel. Le modèle de Sylvanas contient plus de 220 000 polygones. Si c'est le cas pour chaque point pour vérifier l'intersection avec tous ces polygones, vous devez alors effectuer un maximum de 220000 * 1920 * 1080 * 219999 appels à la méthode d'intersection! En 10 minutes, mon ordinateur a pu maîtriser la 10e partie de tous les calculs (2600 polygones sur 220 000), après quoi j'ai eu un quart de travail et je suis parti à la recherche d'une nouvelle méthode.



Sur Internet, je suis tombé sur un moyen très simple et beau qui effectue les mêmes calculsdes milliers de fois plus vite . Cela s'appelle Shadow mapping (création d'une shadow map). Rappelez-vous comment nous avons déterminé les points visibles pour l'observateur - nous avons utilisé zbuffer . La cartographie des ombres fait la même chose! Lors du premier passage, notre caméra sera en position claire et regardant l'objet. Cela générera une carte de profondeur pour la source lumineuse. La carte de profondeur est le zbuffer familier. Dans la seconde passe, nous utilisons cette carte pour déterminer quels sommets doivent être éclairés. Maintenant, je vais enfreindre les règles du bon code et suivre le chemin de la triche - je viens de passer un nouvel objet rasterizer au shader et son utilisation créera une carte de profondeur pour nous.





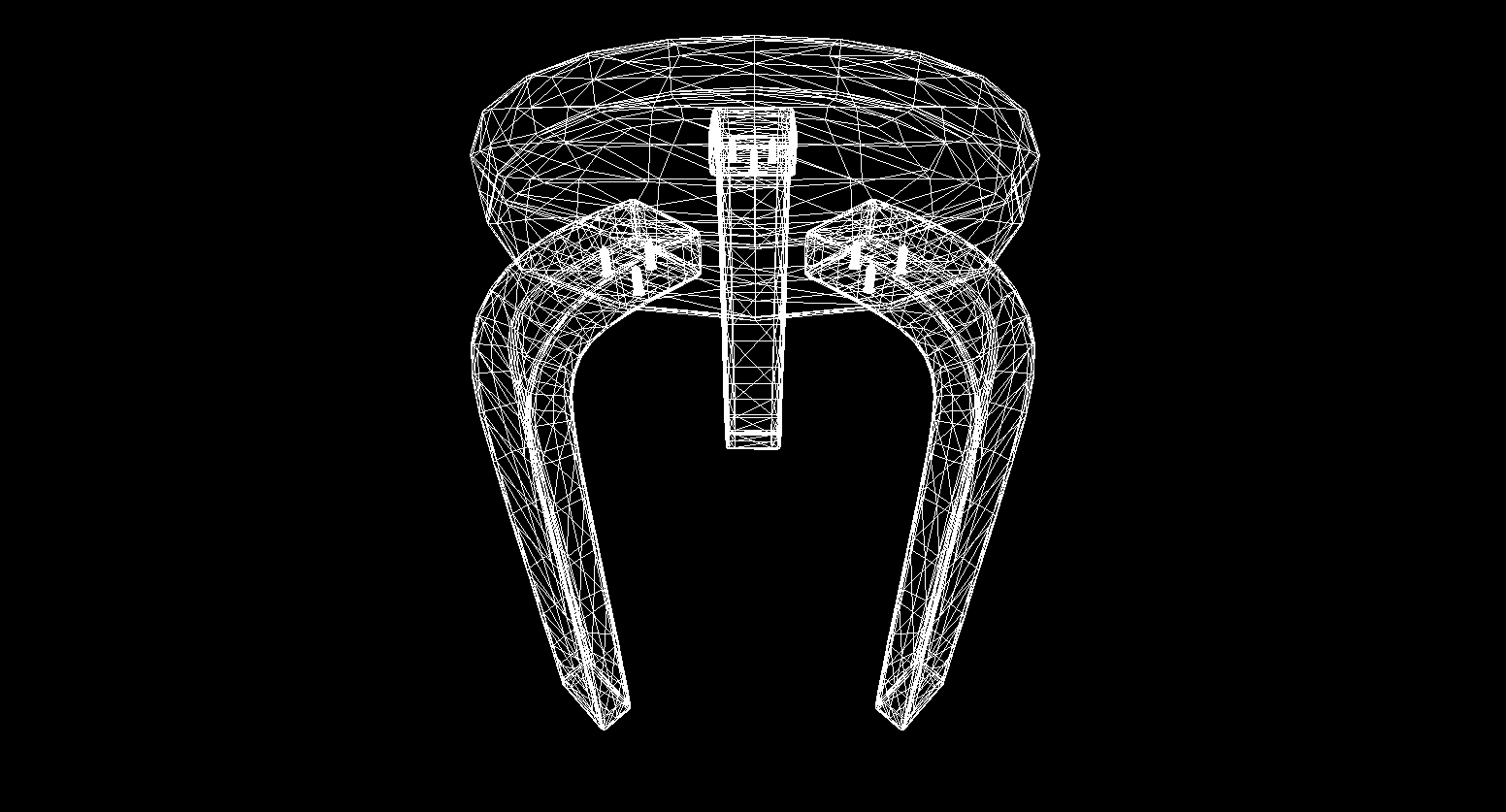
Pour une scène statique, il suffira d'appeler une fois la construction de la carte de profondeur, puis de l'utiliser dans toutes les images. Comme test, j'utilise un modèle moins polygonal du pistolet. Voici l'image de sortie:







Beaucoup d'entre vous ont probablement remarqué les artefacts de ce shader (points noirs non traités par la lumière). Encore une fois, en me tournant vers le réseau omniscient, j'ai trouvé une description de cet effet avec le vilain nom «ombre acné» (pardonnez-moi les personnes d'apparence complexe). L'essence de ces «lacunes» est que nous utilisons la résolution limitée de la carte de profondeur pour définir l'ombre. Cela signifie que plusieurs sommets lors du rendu reçoivent une valeur de la carte de profondeur. Les plus sensibles à un tel artefact sont les surfaces sur lesquelles la lumière tombe à un angle peu profond . L'effet peut être corrigé en augmentant la résolution de rendu des lumières, mais il existe une manière plus élégante . Il consiste à ajouterun décalage spécifique pour la profondeur en fonction de l'angle entre le faisceau lumineux et la surface . Cela peut être fait en utilisant le produit scalaire.

Conclusion

Je me considère comme un débutant en graphisme 3D, je n'exclus pas les erreurs que j'ai commises au cours de la présentation. La seule chose sur laquelle je compte, c'est le résultat pratique obtenu dans le processus de création. Vous pouvez laisser toutes les corrections et optimisations (le cas échéant) dans les commentaires, je me ferai un plaisir de les lire. Lien vers le référentiel du projet .