Deux informaticiens ont trouvé une idée dans un endroit très inattendu qui leur était juste utile pour une percée dans la théorie des graphes

En octobre 2019, Jacob Holm et Eva Rothenberg feuilletaient un ouvrage qu'ils avaient publié quelques mois plus tôt - et se rendirent soudainement compte qu'ils étaient tombés sur quelque chose de sérieux.
Pendant des décennies, les informaticiens ont essayé de concevoir un algorithme rapide pour déterminer si des arêtes peuvent être ajoutées à un graphe particulier afin qu'il reste «planaire», c'est-à-dire que ses arêtes ne se croisent pas. Cependant, personne n'a réussi à améliorer l'algorithme publié il y a plus de 20 ans.
Holm et Rothenberg ont été surpris de constater que dans leur travailil y a une idée qui a permis d'améliorer assez fortement cet algorithme. Elle «a trié l'un des plus grands obstacles à un algorithme réel», a déclaré Holm, informaticien à l'Université de Copenhague. "Peut-être avons-nous entièrement divulgué ce problème."
Le couple s'est précipité pour travailler sur un nouvel article . Ils l'ont présenté en juin lors du Symposium de l' Association for Computing Machinery sur la théorie du calcul , où ils ont détaillé une méthode de vérification de la planéité d'un graphe, exponentiellement supérieure à la version précédente.
«Le nouvel algorithme est vraiment magistral», a déclaré Giuseppe Italiano , un informaticien à l'Université de Louis, co-auteur d'un article de 1996 qui décrit maintenant le deuxième algorithme le plus rapide. "Quand j'ai participé à l'écriture de ce travail, je ne pensais pas que cela pouvait arriver."
Les graphes sont des ensembles de sommets reliés par des arêtes. Ils peuvent être utilisés pour tout étiqueter, des médias sociaux aux réseaux routiers et aux conducteurs électriques sur un tableau. Si dans ce dernier cas le graphique n'est pas plan, les deux conducteurs se croiseront, ce qui entraînera un court-circuit.
En 1913, des graphiques planaires sont apparus dans un puzzle «communal» complexe sur trois maisons , publié dans The Strand Magazine. La publication a demandé aux lecteurs d'établir des communications pour trois maisons, en les reliant chacune à trois vecteurs d'énergie - l'eau, le gaz et l'électricité - afin que les communications ne se croisent pas. Il ne faut pas longtemps pour se rendre compte que cette tâche est insurmontable.
Cependant, dans les cas avec des graphes plus complexes, il n'est pas toujours évident qu'ils soient plans. Il est encore plus difficile de dire si un graphique complexe restera plan lorsque vous commencez à y ajouter des arêtes, comme c'est le cas lors de la planification de nouvelles routes.
Les informaticiens recherchent depuis longtemps un algorithme capable de déterminer rapidement si le changement souhaité peut être effectué afin que le graphe reste planaire, sans passer par chacune des parties du graphe lorsqu'une petite partie seulement est modifiée. L'algorithme de 1996 nécessitait un certain nombre d'étapes pour cela, à peu près proportionnelles à la racine carrée du nombre de sommets du graphe.
«C'est bien mieux que de tout vérifier à partir de zéro à chaque fois, mais pas parfait», a déclaré Holm.
Le nouvel algorithme vérifie la planéité en un certain nombre d'étapes proportionnelles au cube du logarithme du nombre de sommets du graphe - l'amélioration est exponentielle. Holm et Rothenberg de l'Université technique danoise ont réalisé cette accélération en tirant parti d'une propriété spéciale des graphes planaires qu'ils ont découverts l'année dernière.
Pour comprendre leur méthode, vous devez d'abord noter que le même graphe plan peut être dessiné de différentes manières . Toutes les connexions de ces options restent les mêmes, cependant, les bords peuvent être situés les uns par rapport aux autres de différentes manières.
Par exemple, la figure A peut être changée en figure B en inversant le triangle qui compose les sommets 1, 2 et 3 par rapport au bord reliant les sommets 2 et 3. Le haut de la figure B peut également être inversé par rapport aux sommets 4 et 5, obtenant la figure C. différemment, mais désignent le même graphique.
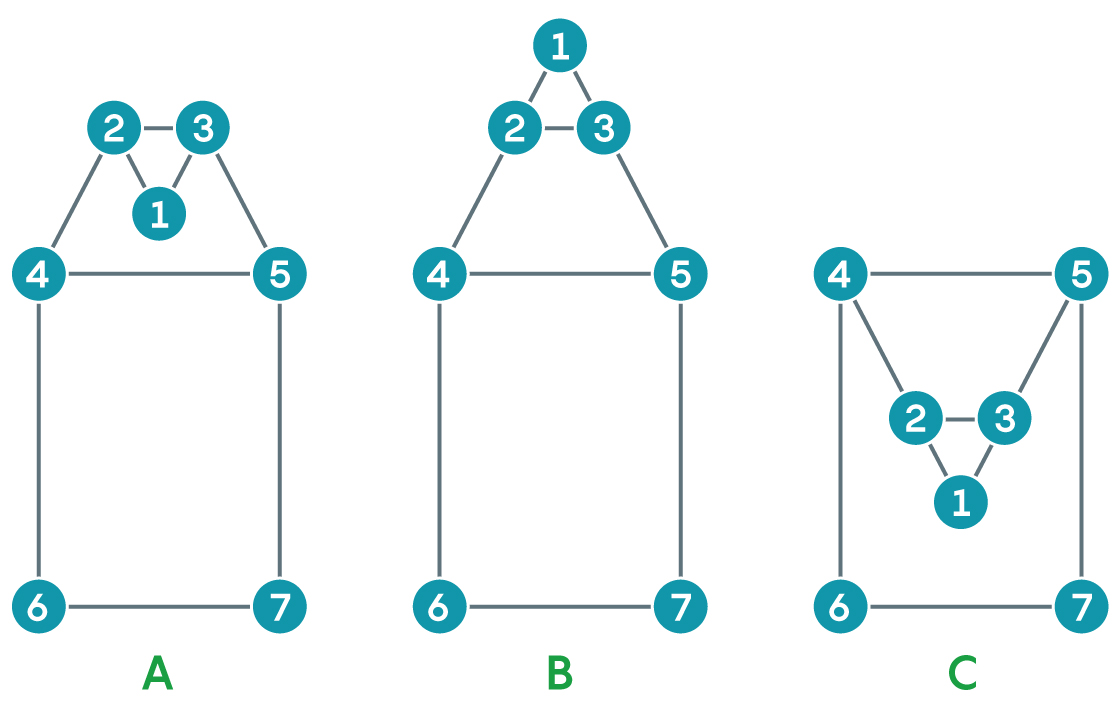
Imaginez maintenant que vous souhaitiez insérer une nouvelle arête qui relie deux sommets d'un graphe plan - disons les sommets 1 et 6. Pour ce faire, vous exécutez une séquence de retournements. Depuis la position de départ à gauche, en deux retournements, vous pouvez transférer le sommet 1 à l'endroit où il peut être connecté au sommet 6 sans croiser d'autres arêtes.

Dans un article de 2019, Holm et Rothenberg ont découvert que certains dessins présentaient plus d'avantages pour l'insertion de bord que d'autres. Ces "bons" motifs n'ont besoin que de quelques retournements pour ajouter un nouveau bord sans casser la planéité.
Ce qu'ils ont réalisé tardivement en octobre, c'est qu'un retournement qui vous rapproche de la position où vous pouvez ajouter une nouvelle arête rapproche également le graphique de l'un des bons modèles qu'ils ont déjà définis. En montrant qu'une séquence de retournements rapproche inévitablement le graphique des motifs préférés, un nouvel algorithme peut être créé pour limiter le nombre de retournements dont vous pourriez avoir besoin pour trouver un moyen d'ajouter un bord (si possible).
«Nous avons réalisé très rapidement qu'avec cette nouvelle analyse le problème pouvait être résolu
un algorithme dont le concept est extrêmement simple », a déclaré Holm.

Jacob Holm et Eva Rothenberg Le
nouvel algorithme effectue un retournement à la fois pour trouver une solution. En conséquence, l'une des deux choses suivantes se produit: soit l'algorithme trouve un moyen d'insérer le bord requis, soit le retournement suivant annule le précédent - après quoi l'algorithme conclut qu'il n'y a aucun moyen d'ajouter un nouveau bord.
«Nous appelons cet algorithme glouton paresseux», a expliqué Rotenberg. "Cela ne fait que les changements nécessaires pour accueillir la nouvelle nervure."
Leur nouvelle méthode se rapproche - mais ne correspond pas - aux performances du meilleur algorithme possible pour de telles tâches. Le nouvel algorithme doit également passer par trop d'étapes pour être utilisé dans la plupart des applications du monde réel - généralement, les graphiques sont assez simples pour être testés en force brute.
Mais pour Holm et Rothenberg, la vitesse de l'algorithme n'est pas aussi importante que les idées qui l'ont accéléré. "Il y a des implications immédiates de cette compréhension", a déclaré Rotenberg.
Italiano pense qu'il pourra éventuellement trouver une réelle utilité. «Tôt ou tard, cela affectera sûrement ce qui est en dehors de l'informatique avec les mathématiques», a-t-il déclaré.
Personne ne sait quand des algorithmes encore plus rapides peuvent apparaître. Cela peut nécessiter une toute nouvelle percée, ou l'ingrédient secret peut déjà exister quelque part, attendant dans les coulisses dans une pile d'anciennes recherches.