
À la recherche d'un objectif
Nous allons sur le site thématique miniclip.com et cherchons une cible. Le choix s'est porté sur le puzzle de couleur Coloruid 2 de la section Puzzles, dans lequel nous devons remplir un terrain de jeu rond avec une couleur en un nombre donné de coups.
Une zone arbitraire est remplie avec la couleur sélectionnée en bas de l'écran, tandis que les zones adjacentes de la même couleur se fondent en une seule.

Entraînement
Nous utiliserons Python. Le bot a été créé à des fins éducatives uniquement. L'article est destiné aux débutants en vision par ordinateur, ce que je suis moi-même.
Le jeu se trouve ici
GitHub du bot ici
Pour que le bot fonctionne, nous avons besoin des modules suivants:
- opencv-python
- Oreiller
- sélénium
Le bot est écrit et testé pour Python 3.8 sur Ubuntu 20.04.1. Nous installons les modules nécessaires dans votre environnement virtuel ou via pip install. De plus, pour que Selenium fonctionne, nous avons besoin d'un geckodriver pour FireFox, vous pouvez le télécharger ici github.com/mozilla/geckodriver/releases
Contrôle du navigateur
Nous avons affaire à un jeu en ligne, nous allons donc d'abord organiser l'interaction avec le navigateur. Pour cela, nous utiliserons Selenium, qui nous fournira une API pour gérer FireFox. Examen du code de la page de jeu. Le puzzle est une toile, qui à son tour est située dans une iframe.
Nous attendons le chargement de la trame avec id = iframe-game et y basculons le contexte du pilote. Ensuite, nous attendons la toile. C'est le seul dans le cadre et est disponible via XPath / html / body / canvas.
wait(self.__driver, 20).until(EC.frame_to_be_available_and_switch_to_it((By.ID, "iframe-game")))
self.__canvas = wait(self.__driver, 20).until(EC.visibility_of_element_located((By.XPATH, "/html/body/canvas")))Ensuite, notre canevas sera disponible via la propriété self .__ canvas. Toute la logique du travail avec le navigateur se résume à prendre une capture d'écran du canevas et à cliquer dessus à une coordonnée donnée.
Code Browser.py complet:
from selenium import webdriver
from selenium.webdriver.support import expected_conditions as EC
from selenium.webdriver.support.ui import WebDriverWait as wait
from selenium.webdriver.common.by import By
class Browser:
def __init__(self, game_url):
self.__driver = webdriver.Firefox()
self.__driver.get(game_url)
wait(self.__driver, 20).until(EC.frame_to_be_available_and_switch_to_it((By.ID, "iframe-game")))
self.__canvas = wait(self.__driver, 20).until(EC.visibility_of_element_located((By.XPATH, "/html/body/canvas")))
def screenshot(self):
return self.__canvas.screenshot_as_png
def quit(self):
self.__driver.quit()
def click(self, click_point):
action = webdriver.common.action_chains.ActionChains(self.__driver)
action.move_to_element_with_offset(self.__canvas, click_point[0], click_point[1]).click().perform()États du jeu
Passons au jeu lui-même. Toute la logique du bot sera implémentée dans la classe Robot. Divisons le gameplay en 7 états et attribuons-leur des méthodes pour les traiter. Choisissons le niveau de formation séparément. Il contient un grand curseur blanc indiquant où cliquer, ce qui empêchera le jeu d'être reconnu correctement.
- Ecran d'accueil
- Écran de sélection de niveau
- Sélection des couleurs au niveau du didacticiel
- Choisir un domaine au niveau de l'enseignement
- Sélection de couleur
- Sélection de la région
- Résultat du déménagement
class Robot:
STATE_START = 0x01
STATE_SELECT_LEVEL = 0x02
STATE_TRAINING_SELECT_COLOR = 0x03
STATE_TRAINING_SELECT_AREA = 0x04
STATE_GAME_SELECT_COLOR = 0x05
STATE_GAME_SELECT_AREA = 0x06
STATE_GAME_RESULT = 0x07
def __init__(self):
self.states = {
self.STATE_START: self.state_start,
self.STATE_SELECT_LEVEL: self.state_select_level,
self.STATE_TRAINING_SELECT_COLOR: self.state_training_select_color,
self.STATE_TRAINING_SELECT_AREA: self.state_training_select_area,
self.STATE_GAME_RESULT: self.state_game_result,
self.STATE_GAME_SELECT_COLOR: self.state_game_select_color,
self.STATE_GAME_SELECT_AREA: self.state_game_select_area,
}Pour une plus grande stabilité du bot, nous vérifierons si le changement d'état du jeu s'est produit avec succès. Si self.state_next_success_condition ne renvoie pas True pendant self.state_timeout, nous continuons à traiter l'état actuel, sinon nous passons à self.state_next. Nous traduirons également la capture d'écran reçue de Selenium dans un format compréhensible pour OpenCV.
import time
import cv2
import numpy
from PIL import Image
from io import BytesIO
class Robot:
def __init__(self):
# …
self.screenshot = []
self.state_next_success_condition = None
self.state_start_time = 0
self.state_timeout = 0
self.state_current = 0
self.state_next = 0
def run(self, screenshot):
self.screenshot = cv2.cvtColor(numpy.array(Image.open(BytesIO(screenshot))), cv2.COLOR_BGR2RGB)
if self.state_current != self.state_next:
if self.state_next_success_condition():
self.set_state_current()
elif time.time() - self.state_start_time >= self.state_timeout
self.state_next = self.state_current
return False
else:
try:
return self.states[self.state_current]()
except KeyError:
self.__del__()
def set_state_current(self):
self.state_current = self.state_next
def set_state_next(self, state_next, state_next_success_condition, state_timeout):
self.state_next_success_condition = state_next_success_condition
self.state_start_time = time.time()
self.state_timeout = state_timeout
self.state_next = state_next
Implémentons la vérification dans les méthodes de gestion des états. Nous attendons le bouton Play sur l'écran de démarrage et cliquez dessus. Si dans les 10 secondes nous n'avons pas reçu l'écran de sélection de niveau, nous revenons à l'étape précédente self.STATE_START, sinon nous procédons au traitement de self.STATE_SELECT_LEVEL.
# …
class Robot:
DEFAULT_STATE_TIMEOUT = 10
# …
def state_start(self):
# Play
# …
if button_play is False:
return False
self.set_state_next(self.STATE_SELECT_LEVEL, self.state_select_level_condition, self.DEFAULT_STATE_TIMEOUT)
return button_play
def state_select_level_condition(self):
#
# …
Vision du bot
Seuil d'image
Définissons les couleurs utilisées dans le jeu. Ce sont 5 couleurs jouables et une couleur de curseur pour le niveau tutoriel. Nous utiliserons COLOR_ALL si nous devons trouver tous les objets, quelle que soit leur couleur. Pour commencer, nous examinerons ce cas.
COLOR_BLUE = 0x01
COLOR_ORANGE = 0x02
COLOR_RED = 0x03
COLOR_GREEN = 0x04
COLOR_YELLOW = 0x05
COLOR_WHITE = 0x06
COLOR_ALL = 0x07
Pour trouver un objet, vous devez d'abord simplifier l'image. Par exemple, prenons le symbole "0" et appliquons-lui un seuil, c'est-à-dire que nous séparerons l'objet de l'arrière-plan. À ce stade, nous ne nous soucions pas de la couleur du symbole. Commençons par convertir l'image en noir et blanc, ce qui en fait un canal. La fonction cv2.cvtColor avec le deuxième argument cv2.COLOR_BGR2GRAY nous aidera avec cela , qui est responsable de la conversion en niveaux de gris. Ensuite, nous effectuons un seuillage à l'aide de cv2.threshold . Tous les pixels de l'image en dessous d'un certain seuil sont mis à 0, tout au-dessus - à 255. Le deuxième argument de la fonction cv2.threshold est responsable de la valeur de seuil . Dans notre cas, n'importe quel nombre peut être là, puisque nous utilisons cv2.THRESH_OTSU et la fonction déterminera elle-même le seuil optimal par la méthode Otsu basée sur l'histogramme de l'image.
image = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
_, thresh = cv2.threshold(image, 0, 255, cv2.THRESH_OTSU)

Segmentation des couleurs
Encore plus intéressant. Compliquons la tâche et trouvons tous les symboles rouges sur l'écran de sélection de niveau.

Par défaut, toutes les images OpenCV sont stockées au format BGR. HSV (teinte, saturation, valeur - teinte, saturation, valeur) est plus approprié pour la segmentation des couleurs. Son avantage par rapport au RVB est que HSV sépare la couleur de la saturation et de la luminosité. La teinte est codée par un canal Hue. Prenons un rectangle vert clair comme exemple et diminuons progressivement sa luminosité.
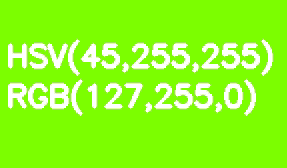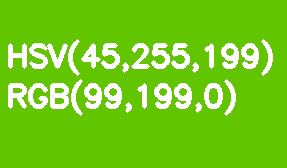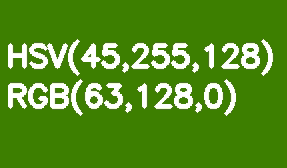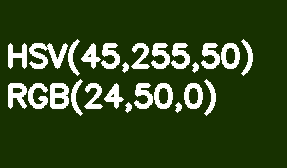
Contrairement à RVB, cette transformation semble intuitive dans HSV - nous diminuons simplement la valeur du canal Valeur ou Luminosité. Il convient de noter ici que dans le modèle de référence, l'échelle de teinte Hue varie de 0 à 360 °. Notre couleur vert clair correspond à 90 °. Afin d'adapter cette valeur dans un canal 8 bits, elle doit être divisée par 2.
La segmentation des couleurs fonctionne avec des plages, pas une seule couleur. Vous pouvez déterminer la plage de manière empirique, mais il est plus facile d'écrire un petit script.
import cv2
import numpy as numpy
image_path = "tests_data/SELECT_LEVEL.png"
hsv_max_upper = 0, 0, 0
hsv_min_lower = 255, 255, 255
def bite_range(value):
value = 255 if value > 255 else value
return 0 if value < 0 else value
def pick_color(event, x, y, flags, param):
if event == cv2.EVENT_LBUTTONDOWN:
global hsv_max_upper
global hsv_min_lower
global image_hsv
hsv_pixel = image_hsv[y, x]
hsv_max_upper = bite_range(max(hsv_max_upper[0], hsv_pixel[0]) + 1), \
bite_range(max(hsv_max_upper[1], hsv_pixel[1]) + 1), \
bite_range(max(hsv_max_upper[2], hsv_pixel[2]) + 1)
hsv_min_lower = bite_range(min(hsv_min_lower[0], hsv_pixel[0]) - 1), \
bite_range(min(hsv_min_lower[1], hsv_pixel[1]) - 1), \
bite_range(min(hsv_min_lower[2], hsv_pixel[2]) - 1)
print('HSV range: ', (hsv_min_lower, hsv_max_upper))
hsv_mask = cv2.inRange(image_hsv, numpy.array(hsv_min_lower), numpy.array(hsv_max_upper))
cv2.imshow("HSV Mask", hsv_mask)
image = cv2.imread(image_path)
cv2.namedWindow('Original')
cv2.setMouseCallback('Original', pick_color)
image_hsv = cv2.cvtColor(image, cv2.COLOR_BGR2HSV)
cv2.imshow("Original", image)
cv2.waitKey(0)
cv2.destroyAllWindows()
Lançons-le avec notre capture d'écran.

Cliquez sur la couleur rouge et regardez le masque résultant. Si la sortie ne nous convient pas, on choisit les nuances de rouge, en augmentant la portée et la surface du masque. Le script est basé sur la fonction cv2.inRange , qui agit comme un filtre de couleur et renvoie une image de seuil pour une plage de couleurs donnée.
Arrêtons-nous sur les gammes suivantes:
COLOR_HSV_RANGE = {
COLOR_BLUE: ((112, 151, 216), (128, 167, 255)),
COLOR_ORANGE: ((8, 251, 93), (14, 255, 255)),
COLOR_RED: ((167, 252, 223), (171, 255, 255)),
COLOR_GREEN: ((71, 251, 98), (77, 255, 211)),
COLOR_YELLOW: ((27, 252, 51), (33, 255, 211)),
COLOR_WHITE: ((0, 0, 159), (7, 7, 255)),
}Trouver des contours
Revenons à notre écran de sélection de niveau. Appliquons le filtre de couleur de plage rouge que nous venons de définir et passons le seuil trouvé à cv2.findContours . La fonction nous trouvera les contours des éléments rouges. Nous spécifions cv2.RETR_EXTERNAL comme deuxième argument - nous n'avons besoin que de contours externes, et comme troisième cv2.CHAIN_APPROX_SIMPLE - nous nous intéressons aux contours droits, économisons de la mémoire et ne stockons que leurs sommets.
thresh = cv2.inRange(image, self.COLOR_HSV_RANGE[self.COLOR_RED][0], self.COLOR_HSV_RANGE[self.COLOR_RED][1])
contours, _ = cv2.findContours(thresh, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE
Suppression du bruit
Les contours résultants contiennent beaucoup de bruit de fond. Pour le supprimer, nous utiliserons la propriété de nos nombres. Ils sont constitués de rectangles parallèles aux axes de coordonnées. Nous itérons sur tous les chemins et adaptons chacun dans le rectangle minimum en utilisant cv2.minAreaRect . Le rectangle est défini par 4 points. Si notre rectangle est parallèle aux axes, alors l'une des coordonnées de chaque paire de points doit correspondre. Cela signifie que nous aurons un maximum de 4 valeurs uniques si nous représentons les coordonnées du rectangle comme un tableau unidimensionnel. De plus, nous filtrerons les rectangles trop longs, dont le rapport hauteur / largeur est supérieur à 3 pour 1. Pour ce faire, nous trouverons leur largeur et leur longueur en utilisant cv2.boundingRect .
squares = []
for cnt in contours:
rect = cv2.minAreaRect(cnt)
square = cv2.boxPoints(rect)
square = numpy.int0(square)
(_, _, w, h) = cv2.boundingRect(square)
a = max(w, h)
b = min(w, h)
if numpy.unique(square).shape[0] <= 4 and a <= b * 3:
squares.append(numpy.array([[square[0]], [square[1]], [square[2]], [square[3]]]))

Combiner les contours
Mieux maintenant. Nous devons maintenant combiner les rectangles trouvés dans un contour commun de symboles. Nous avons besoin d'une image intermédiaire. Créons-le avec numpy.zeros_like . La fonction crée une copie de la matrice d'image tout en conservant sa forme et sa taille, puis la remplit de zéros. En d'autres termes, nous avons obtenu une copie de notre image originale remplie d'un fond noir. Nous le convertissons en 1 canal et appliquons les contours trouvés en utilisant cv2.drawContours , en les remplissant de blanc. Nous obtenons un seuil binaire auquel nous pouvons appliquer cv2.dilate . La fonction élargit la zone blanche en connectant des rectangles séparés, dont la distance est inférieure à 5 pixels. Une fois de plus, j'appelle cv2.findContours et j'obtiens les contours des nombres rouges.
image_zero = numpy.zeros_like(image)
image_zero = cv2.cvtColor(image_zero, cv2.COLOR_BGR2RGB)
cv2.drawContours(image_zero, contours_of_squares, -1, (255, 255, 255), -1)
_, thresh = cv2.threshold(image_zero, 0, 255, cv2.THRESH_OTSU)
kernel = numpy.ones((5, 5), numpy.uint8)
thresh = cv2.dilate(thresh, kernel, iterations=1)
dilate_contours, _ = cv2.findContours(thresh, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)

Le bruit restant est filtré par la zone de contour à l'aide de cv2.contourArea . Supprimez tout ce qui est inférieur à 500 pixels².
digit_contours = [cnt for cnt in digit_contours if cv2.contourArea(cnt) > 500]
Maintenant c'est génial. Implémentons tout ce qui précède dans notre classe Robot.
# ...
class Robot:
# ...
def get_dilate_contours(self, image, color_inx, distance):
thresh = self.get_color_thresh(image, color_inx)
if thresh is False:
return []
kernel = numpy.ones((distance, distance), numpy.uint8)
thresh = cv2.dilate(thresh, kernel, iterations=1)
contours, _ = cv2.findContours(thresh, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
return contours
def get_color_thresh(self, image, color_inx):
if color_inx == self.COLOR_ALL:
image = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
_, thresh = cv2.threshold(image, 0, 255, cv2.THRESH_OTSU)
else:
image = cv2.cvtColor(image, cv2.COLOR_BGR2HSV)
thresh = cv2.inRange(image, self.COLOR_HSV_RANGE[color_inx][0], self.COLOR_HSV_RANGE[color_inx][1])
return thresh
def filter_contours_of_rectangles(self, contours):
squares = []
for cnt in contours:
rect = cv2.minAreaRect(cnt)
square = cv2.boxPoints(rect)
square = numpy.int0(square)
(_, _, w, h) = cv2.boundingRect(square)
a = max(w, h)
b = min(w, h)
if numpy.unique(square).shape[0] <= 4 and a <= b * 3:
squares.append(numpy.array([[square[0]], [square[1]], [square[2]], [square[3]]]))
return squares
def get_contours_of_squares(self, image, color_inx, square_inx):
thresh = self.get_color_thresh(image, color_inx)
if thresh is False:
return False
contours, _ = cv2.findContours(thresh, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
contours_of_squares = self.filter_contours_of_rectangles(contours)
if len(contours_of_squares) < 1:
return False
image_zero = numpy.zeros_like(image)
image_zero = cv2.cvtColor(image_zero, cv2.COLOR_BGR2RGB)
cv2.drawContours(image_zero, contours_of_squares, -1, (255, 255, 255), -1)
dilate_contours = self.get_dilate_contours(image_zero, self.COLOR_ALL, 5)
dilate_contours = [cnt for cnt in dilate_contours if cv2.contourArea(cnt) > 500]
if len(dilate_contours) < 1:
return False
else:
return dilate_contours
Reconnaissance des nombres
Ajoutons la possibilité de reconnaître les nombres. Pourquoi avons nous besoin de ça?
# …
class Robot:
# ...
SQUARE_BIG_SYMBOL = 0x01
SQUARE_SIZES = {
SQUARE_BIG_SYMBOL: 9,
}
IMAGE_DATA_PATH = "data/"
def __init__(self):
# ...
self.dilate_contours_bi_data = {}
for image_file in os.listdir(self.IMAGE_DATA_PATH):
image = cv2.imread(self.IMAGE_DATA_PATH + image_file)
contour_inx = os.path.splitext(image_file)[0]
color_inx = self.COLOR_RED
dilate_contours = self.get_dilate_contours_by_square_inx(image, color_inx, self.SQUARE_BIG_SYMBOL)
self.dilate_contours_bi_data[contour_inx] = dilate_contours[0]
def get_dilate_contours_by_square_inx(self, image, color_inx, square_inx):
distance = math.ceil(self.SQUARE_SIZES[square_inx] / 2)
return self.get_dilate_contours(image, color_inx, distance)OpenCV utilise la fonction cv2.matchShapes pour comparer les contours en fonction des moments Hu . Il nous cache les détails de l'implémentation en prenant deux chemins en entrée et en renvoyant le résultat de la comparaison sous forme de nombre. Plus il est petit, plus les contours sont similaires.
cv2.matchShapes(dilate_contour, self.dilate_contours_bi_data['digit_' + str(digit)], cv2.CONTOURS_MATCH_I1, 0)Comparez le contour actuel digit_contour avec toutes les normes et trouvez la valeur minimale de cv2.matchShapes. Si la valeur minimale est inférieure à 0,15, le chiffre est considéré comme reconnu. Le seuil de la valeur minimale a été trouvé empiriquement. Combinons également des symboles étroitement espacés en un seul nombre.
# …
class Robot:
# …
def scan_digits(self, image, color_inx, square_inx):
result = []
contours_of_squares = self.get_contours_of_squares(image, color_inx, square_inx)
before_digit_x, before_digit_y = (-100, -100)
if contours_of_squares is False:
return result
for contour_of_square in reversed(contours_of_squares):
crop_image = self.crop_image_by_contour(image, contour_of_square)
dilate_contours = self.get_dilate_contours_by_square_inx(crop_image, self.COLOR_ALL, square_inx)
if (len(dilate_contours) < 1):
continue
dilate_contour = dilate_contours[0]
match_shapes = {}
for digit in range(0, 10):
match_shapes[digit] = cv2.matchShapes(dilate_contour, self.dilate_contours_bi_data['digit_' + str(digit)], cv2.CONTOURS_MATCH_I1, 0)
min_match_shape = min(match_shapes.items(), key=lambda x: x[1])
if len(min_match_shape) > 0 and (min_match_shape[1] < self.MAX_MATCH_SHAPES_DIGITS):
digit = min_match_shape[0]
rect = cv2.minAreaRect(contour_of_square)
box = cv2.boxPoints(rect)
box = numpy.int0(box)
(digit_x, digit_y, digit_w, digit_h) = cv2.boundingRect(box)
if abs(digit_y - before_digit_y) < digit_y * 0.3 and abs(
digit_x - before_digit_x) < digit_w + digit_w * 0.5:
result[len(result) - 1][0] = int(str(result[len(result) - 1][0]) + str(digit))
else:
result.append([digit, self.get_contour_centroid(contour_of_square)])
before_digit_x, before_digit_y = digit_x + (digit_w / 2), digit_y
return resultEn sortie, la méthode self.scan_digits retournera un tableau contenant le chiffre reconnu et la coordonnée du clic dessus. Le point de clic sera le centre de gravité de son contour.
# …
class Robot:
# …
def get_contour_centroid(self, contour):
moments = cv2.moments(contour)
return int(moments["m10"] / moments["m00"]), int(moments["m01"] / moments["m00"])Nous nous réjouissons de l'outil de reconnaissance numérique reçu, mais pas pour longtemps. Les moments Hu, mis à part l'échelle, sont également invariants à la rotation et à la spécularité. Par conséquent, le bot confondra les nombres 6 et 9/2 et 5. Ajoutons une vérification de vertex supplémentaire pour ces symboles. 6 et 9 seront distingués par le point supérieur droit. S'il est en dessous du centre horizontal, alors il est 6 et 9 pour le contraire. Pour les paires 2 et 5, vérifiez si le point supérieur droit se trouve sur la bordure droite du symbole.
if digit == 6 or digit == 9:
extreme_bottom_point = digit_contour[digit_contour[:, :, 1].argmax()].flatten()
x_points = digit_contour[:, :, 0].flatten()
extreme_right_points_args = numpy.argwhere(x_points == numpy.amax(x_points))
extreme_right_points = digit_contour[extreme_right_points_args]
extreme_top_right_point = extreme_right_points[extreme_right_points[:, :, :, 1].argmin()].flatten()
if extreme_top_right_point[1] > round(extreme_bottom_point[1] / 2):
digit = 6
else:
digit = 9
if digit == 2 or digit == 5:
extreme_right_point = digit_contour[digit_contour[:, :, 0].argmax()].flatten()
y_points = digit_contour[:, :, 1].flatten()
extreme_top_points_args = numpy.argwhere(y_points == numpy.amin(y_points))
extreme_top_points = digit_contour[extreme_top_points_args]
extreme_top_right_point = extreme_top_points[extreme_top_points[:, :, :, 0].argmax()].flatten()
if abs(extreme_right_point[0] - extreme_top_right_point[0]) > 0.05 * extreme_right_point[0]:
digit = 2
else:
digit = 5

Analyser le terrain de jeu
Sautons le niveau d'entraînement, il est scripté en cliquant sur le curseur blanc et commencez à jouer.
Imaginons le terrain de jeu comme un réseau. Chaque zone de couleur sera un nœud lié à des voisins adjacents. Créons une classe self.ColorArea qui décrira la zone de couleur / le nœud.
class ColorArea:
def __init__(self, color_inx, click_point, contour):
self.color_inx = color_inx #
self.click_point = click_point #
self.contour = contour #
self.neighbors = [] # Définissons une liste de nœuds self.color_areas et une liste de la fréquence à laquelle la couleur apparaît sur le terrain de jeu self.color_areas_color_count . Recadrez le terrain de jeu à partir de la capture d'écran de la toile.
image[pt1[1]:pt2[1], pt1[0]:pt2[0]]Où pt1, pt2 sont les points extrêmes de l'image. Nous parcourons toutes les couleurs du jeu et appliquons la méthode self.get_dilate_contours à chacune . Trouver le contour du nœud est similaire à la façon dont nous recherchions le contour général des symboles, à la différence qu'il n'y a pas de bruit sur le terrain de jeu. La forme des nœuds peut être concave ou avoir un trou, de sorte que le centre de gravité tombe hors de la forme et ne convient pas comme coordonnée pour un clic. Pour ce faire, trouvez le point le plus haut et déposez-le de 20 pixels. La méthode n'est pas universelle, mais dans notre cas, elle fonctionne.
self.color_areas = []
self.color_areas_color_count = [0] * self.SELECT_COLOR_COUNT
image = self.crop_image_by_rectangle(self.screenshot, numpy.array(self.GAME_MAIN_AREA))
for color_inx in range(1, self.SELECT_COLOR_COUNT + 1):
dilate_contours = self.get_dilate_contours(image, color_inx, 10)
for dilate_contour in dilate_contours:
click_point = tuple(
dilate_contour[dilate_contour[:, :, 1].argmin()].flatten() + [0, int(self.CLICK_AREA)])
self.color_areas_color_count[color_inx - 1] += 1
color_area = self.ColorArea(color_inx, click_point, dilate_contour)
self.color_areas.append(color_area)
Zones de liaison
Nous considérerons les zones comme voisines si la distance entre leurs contours est inférieure à 15 pixels. Nous itérons sur chaque nœud avec chacun, en sautant la comparaison si leurs couleurs correspondent.
blank_image = numpy.zeros_like(image)
blank_image = cv2.cvtColor(blank_image, cv2.COLOR_BGR2GRAY)
for color_area_inx_1 in range(0, len(self.color_areas)):
for color_area_inx_2 in range(color_area_inx_1 + 1, len(self.color_areas)):
color_area_1 = self.color_areas[color_area_inx_1]
color_area_2 = self.color_areas[color_area_inx_2]
if color_area_1.color_inx == color_area_2.color_inx:
continue
common_image = cv2.drawContours(blank_image.copy(), [color_area_1.contour, color_area_2.contour], -1, (255, 255, 255), cv2.FILLED)
kernel = numpy.ones((15, 15), numpy.uint8)
common_image = cv2.dilate(common_image, kernel, iterations=1)
common_contour, _ = cv2.findContours(common_image, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
if len(common_contour) == 1:
self.color_areas[color_area_inx_1].neighbors.append(color_area_inx_2)
self.color_areas[color_area_inx_2].neighbors.append(color_area_inx_1)
Nous recherchons le déménagement optimal
Nous avons toutes les informations sur le terrain de jeu. Commençons par choisir un mouvement. Pour cela, nous avons besoin d'un index de nœud et d'une couleur. Le nombre d'options de déplacement peut être déterminé par la formule:
Options de déplacement = Nombre de nœuds * Nombre de couleurs - 1
Pour le terrain de jeu précédent, nous avons 7 * (5-1) = 28 options. Il n'y en a pas beaucoup, nous pouvons donc parcourir tous les mouvements et choisir celui qui est optimal. Définissons les options comme une matrice
select_color_weights , dans laquelle la ligne sera l'index du nœud, la colonne d'index de couleur et la cellule de poids de déplacement. Nous devons réduire le nombre de nœuds à un, donc nous donnerons la priorité aux zones qui ont une couleur unique sur le plateau et qui disparaîtront une fois que nous y passerons. Donnons +10 au poids pour toutes les lignes de nœuds avec une couleur unique. À quelle fréquence la couleur apparaît-elle sur le terrain de jeu, nous avons précédemment collecté dansself.color_areas_color_count
if self.color_areas_color_count[color_area.color_inx - 1] == 1:
select_color_weight = [x + 10 for x in select_color_weight]
Ensuite, regardons les couleurs des zones adjacentes. Si le nœud a des voisins de color_inx et que leur nombre est égal au nombre total de cette couleur sur le terrain de jeu, attribuez +10 au poids de la cellule. Cela supprimera également la couleur color_inx du champ.
for color_inx in range(0, len(select_color_weight)):
color_count = select_color_weight[color_inx]
if color_count != 0 and self.color_areas_color_count[color_inx] == color_count:
select_color_weight[color_inx] += 10Donnons +1 au poids de cellule pour chaque voisin de la même couleur. Autrement dit, si nous avons 3 voisins rouges, la cellule rouge recevra +3 à son poids.
for select_color_weight_inx in color_area.neighbors:
neighbor_color_area = self.color_areas[select_color_weight_inx]
select_color_weight[neighbor_color_area.color_inx - 1] += 1Après avoir collecté tous les poids, nous trouvons le mouvement avec le poids maximum. Définissons à quel nœud et à quelle couleur il appartient.
max_index = select_color_weights.argmax()
self.color_area_inx_next = max_index // self.SELECT_COLOR_COUNT
select_color_next = (max_index % self.SELECT_COLOR_COUNT) + 1
self.set_select_color_next(select_color_next)Code complet pour déterminer le mouvement optimal.
# …
class Robot:
# …
def scan_color_areas(self):
self.color_areas = []
self.color_areas_color_count = [0] * self.SELECT_COLOR_COUNT
image = self.crop_image_by_rectangle(self.screenshot, numpy.array(self.GAME_MAIN_AREA))
for color_inx in range(1, self.SELECT_COLOR_COUNT + 1):
dilate_contours = self.get_dilate_contours(image, color_inx, 10)
for dilate_contour in dilate_contours:
click_point = tuple(
dilate_contour[dilate_contour[:, :, 1].argmin()].flatten() + [0, int(self.CLICK_AREA)])
self.color_areas_color_count[color_inx - 1] += 1
color_area = self.ColorArea(color_inx, click_point, dilate_contour, [0] * self.SELECT_COLOR_COUNT)
self.color_areas.append(color_area)
blank_image = numpy.zeros_like(image)
blank_image = cv2.cvtColor(blank_image, cv2.COLOR_BGR2GRAY)
for color_area_inx_1 in range(0, len(self.color_areas)):
for color_area_inx_2 in range(color_area_inx_1 + 1, len(self.color_areas)):
color_area_1 = self.color_areas[color_area_inx_1]
color_area_2 = self.color_areas[color_area_inx_2]
if color_area_1.color_inx == color_area_2.color_inx:
continue
common_image = cv2.drawContours(blank_image.copy(), [color_area_1.contour, color_area_2.contour],
-1, (255, 255, 255), cv2.FILLED)
kernel = numpy.ones((15, 15), numpy.uint8)
common_image = cv2.dilate(common_image, kernel, iterations=1)
common_contour, _ = cv2.findContours(common_image, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
if len(common_contour) == 1:
self.color_areas[color_area_inx_1].neighbors.append(color_area_inx_2)
self.color_areas[color_area_inx_2].neighbors.append(color_area_inx_1)
def analysis_color_areas(self):
select_color_weights = []
for color_area_inx in range(0, len(self.color_areas)):
color_area = self.color_areas[color_area_inx]
select_color_weight = numpy.array([0] * self.SELECT_COLOR_COUNT)
for select_color_weight_inx in color_area.neighbors:
neighbor_color_area = self.color_areas[select_color_weight_inx]
select_color_weight[neighbor_color_area.color_inx - 1] += 1
for color_inx in range(0, len(select_color_weight)):
color_count = select_color_weight[color_inx]
if color_count != 0 and self.color_areas_color_count[color_inx] == color_count:
select_color_weight[color_inx] += 10
if self.color_areas_color_count[color_area.color_inx - 1] == 1:
select_color_weight = [x + 10 for x in select_color_weight]
color_area.set_select_color_weights(select_color_weight)
select_color_weights.append(select_color_weight)
select_color_weights = numpy.array(select_color_weights)
max_index = select_color_weights.argmax()
self.color_area_inx_next = max_index // self.SELECT_COLOR_COUNT
select_color_next = (max_index % self.SELECT_COLOR_COUNT) + 1
self.set_select_color_next(select_color_next)
Ajoutons la possibilité de se déplacer entre les niveaux et de profiter du résultat. Le bot fonctionne de manière stable et termine le jeu en une seule session.
Production
Le bot créé n'a aucune utilité pratique. Mais l'auteur de l'article espère sincèrement qu'une description détaillée des principes de base d'OpenCV aidera les débutants à comprendre cette bibliothèque au stade initial.