Dans la partie précédente, nous nous sommes arrêtés sur le fait qu'il est nécessaire d'obtenir la couleur d'un pixel à partir de la carte raster originale par des coordonnées géodésiques (latitude,
longitude), déjà traduites dans le SC de cette carte.
Les coordonnées géodésiques sont définies sur la surface de l'ellipsoïde et les coordonnées des pixels sur le plan, c'est-à-dire vous avez besoin d'un moyen de passer d'une surface convexe à une surface plane. Le problème est qu'une surface convexe (imaginez qu'une sorte de dessin ou une grille de coordonnées lui soit appliquée) ne peut pas être transférée sur une surface plane sans aucune distorsion. Peut être déformé: forme (angles), surface, dimensions linéaires. Il y a, bien sûr, la possibilité, et pas la seule, de transférer sur une surface plane sans déformer une seule chose, mais le reste sera inévitablement déformé.

Evidemment, sur des échelles plus petites (planète entière, continent), les distorsions sont plus prononcées que sur les plus grandes (région, ville), et sur la plus grande (plan d'une petite zone), on n'en parle pas du tout, car la surface de l'ellipsoïde à de telles échelles ne se distingue plus du plan.
Nous arrivons ici au concept de projection cartographique. Je ne donnerai pas d'exemples avec des images de projection d'une sphère sur un cylindre ou un cône avec développement ultérieur, pour nous il est maintenant important de généraliser.
Une projection cartographique est une manière mathématiquement définie de cartographier la surface d'un ellipsoïde sur un plan. En termes simples, ce sont des formules mathématiques pour convertir des coordonnées géodésiques (latitude, longitude) en coordonnées cartésiennes plates - exactement ce dont nous avons besoin.
Une grande variété de projections cartographiques a été inventée, elles trouvent toutes une application à leurs propres fins: de taille égale (dans laquelle la zone est préservée) pour les cartes politiques, les cartes de sol, conformes (dans lesquelles la forme est préservée) - pour la navigation, équidistante (maintenir l'échelle dans la direction choisie) - pour l'ordinateur traitement et stockage de tableaux de géodonnées. Il existe également des projections qui combinent les caractéristiques mentionnées ci-dessus dans certaines proportions, il y a des projections complètement ésotériques. Des exemples de projections sont disponibles sur Wikipedia sur la page Liste des projections cartographiques.
Pour chaque projection, soit des formules exactes sont dérivées, soit sous la forme d'une somme de séries convergentes infinies, et dans ce dernier cas, il peut même y avoir plusieurs options. Les formules pour les projections convertissent la latitude et la longitude en coordonnées cartésiennes, généralement l'unité de mesure dans ces coordonnées est le mètre. Cette grille rectangulaire d'un mètre peut parfois être tracée sur une carte (sous la forme d'une grille kilométrique), mais dans la plupart des cas, elle n'est pas tracée. Mais nous savons maintenant qu'il existe toujours sous une forme implicite. L'échelle de la carte, qui est indiquée sur la carte, est juste calculée par rapport à la taille de cette grille. Il faut bien comprendre qu'un mètre sur une telle grille de coordonnées correspond à 1 mètre au sol non pas sur toute la carte, mais seulement en certains points, le long d'une certaine ligne, ou le long de lignes dans une certaine direction,dans le reste des points ou directions, des distorsions apparaissent et 1 mètre au sol ne correspond pas à 1 mètre de la grille de coordonnées.
Une petite digression. La fonction de la première partie de l'article WGS84_XYZ est précisément la transformation des coordonnées du WGS84 SC en coordonnées rectangulaires, mais exprimées non en mètres, mais en pixels. Comme vous pouvez le voir, la formule est extrêmement simple, si la projection de Mercator n'était pas utilisée sur une sphère, mais sur un ellipsoïde, alors la formule serait plus compliquée. C'est pourquoi, afin de faciliter la vie des navigateurs, une sphère a été choisie, puis la projection WebMercator s'est enracinée dans sa sphère, pour laquelle elle est souvent critiquée.
Pour mes besoins, j'ai utilisé un document intitulé "Projections cartographiques utilisées par le US Geological Survey" au format pdf, disponible sur Internet. Le document fournit des instructions détaillées pour chaque projection sur laquelle il est facile d'écrire une fonction de transformation dans un langage de programmation.
Continuons à écrire notre algorithme. Implémentons l'une des projections populaires appelées Transverse Mercator et l'une de ses variantes appelée projection Gauss-Kruger.
struct TransverseMercatorParam {
struct Ellipsoid *ep;
double k; /* */
double lat0; /* ( ) */
double lon0; /* ( ) */
double n0; /* */
double e0; /* */
double zw; /* ( ) */
double zs; /* */
//
double e2__a2k2, ie2__a2k2, m0, mp, imp;
double f0, f2, f4, f6;
double m1, m2, m4, m6;
double q, q1, q2, q3, q4, q6, q7, q8;
double q11, q12, q13, q14, q15, q16, q17, q18;
// - 2
double apk, n, b, c, d;
double b1, b2, b3, b4;
};
struct TransverseMercatorParam TM_GaussKruger = {
.ep = &Ellipsoid_Krasovsky,
.zw = rad(6,0,0),
.lon0 = -rad(3,0,0),
.e0 = 5e5,
.zs = 1e6,
};
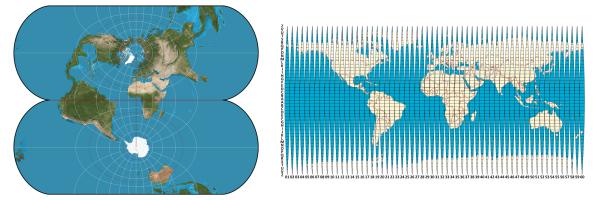
Une caractéristique de la projection transversale de Mercator est qu'elle est conforme, c'est-à-dire que la forme des objets sur la carte et les angles sont préservés, ainsi que le fait que l'échelle est conservée le long d'un méridien central. La projection convient à l'ensemble du globe, mais les distorsions augmentent avec la distance du méridien central, de sorte que toute la surface de la terre est coupée en bandes étroites le long des méridiens, appelés zones, pour chacune desquelles son propre méridien central est utilisé. Des exemples de mise en œuvre de telles projections sont la projection de Gauss-Kruger et l'UTM, dans lesquels la méthode de répartition des coordonnées sur les zones est également définie, c'est-à-dire défini et le même nom SC.
Et, en fait, le code des fonctions d'initialisation et de transformation de coordonnées. Dans la fonction d'initialisation, les constantes sont calculées une seule fois, qui seront réutilisées par la fonction de conversion.
void setupTransverseMercator(struct TransverseMercatorParam *pp) {
double sin_lat, cos_lat, cos2_lat;
double q, n, rk, ak;
if (!pp->k)
pp->k = 1.0;
sin_lat = sin(pp->lat0);
cos_lat = cos(pp->lat0);
cos2_lat = cos_lat * cos_lat;
q = pp->ep->e2 / (1 - pp->ep->e2);
// n = (a-b)/(a+b)
n = (pp->ep->a - pp->ep->b) / (pp->ep->a + pp->ep->b);
rk = (pp->ep->a + pp->ep->b) * pp->k / 2;
ak = pp->ep->a * pp->k;
pp->e2__a2k2 = pp->ep->e2 / (ak * ak);
pp->ie2__a2k2 = (1 - pp->ep->e2) / (ak * ak);
pp->f6 = 1097.0/4 * n*n*n*n;
pp->f4 = (151.0/3 - 3291.0/8 * n) * n*n*n;
pp->f2 = (21.0/2 + (-151.0/3 + 5045.0/32 * n) * n) * n*n;
pp->f0 = (3.0 + (-21.0/4 + (31.0/4 - 657.0/64 * n) * n) * n) * n;
pp->m6 = rk * 315.0/4 * n*n*n*n;
pp->m4 = rk * (-70.0/3 - 945.0/8 * n) * n*n*n;
pp->m2 = rk * (15.0/2 + (70.0/3 + 1515.0/32 * n) * n) * n*n;
pp->m1 = rk * (-3.0 + (-15.0/4 + (-4.0 - 255.0/64 * n) * n) * n) * n;
// polar distance
pp->mp = rk * (1.0 + (1.0/4 + 1.0/64 * n*n) * n*n);
pp->imp = 1 / pp->mp;
pp->m0 = pp->n0 - pp->mp * pp->lat0 - sin_lat * cos_lat *
(pp->m1 + (pp->m2 + (pp->m4 + pp->m6 * cos2_lat) * cos2_lat) * cos2_lat);
pp->q = q;
pp->q1 = 1.0/6 * q*q;
pp->q2 = 3.0/8 * q;
pp->q3 = 5.0/6 * q;
pp->q4 = 1.0/6 - 11.0/24 * q;
pp->q6 = 1.0/6 * q;
pp->q7 = 3.0/5 * q;
pp->q8 = 1.0/5 - 29.0/60 * q;
pp->q11 = - 5.0/12 * q;
pp->q12 = -5.0/24 + 3.0/8 * q;
pp->q13 = - 1.0/240 * q*q;
pp->q14 = 149.0/360 * q;
pp->q15 = 61.0/720 - 63.0/180 * q;
pp->q16 = - 1.0/40 * q*q;
pp->q17 = - 1.0/60 * q;
pp->q18 = 1.0/24 + 1.0/15 * q;
// - 2
double e2 = pp->ep->e2;
pp->apk = ak * (1 + n*n / 4 + n*n*n*n / 64) / (1 + n);
pp->n = n;
pp->b = (5 - e2) * e2 * e2 / 6;
pp->c = (104 - 45 * e2) * e2 * e2 * e2 / 120;
pp->d = 1237.0/1260 * e2 * e2 * e2 * e2;
pp->b1 = (1.0/2 + (-2.0/3 + (5.0/16 + 41.0/180 * n) * n) * n) * n;
pp->b2 = (13.0/48 + (-3.0/5 + 557.0/1440 * n) * n) * n*n;
pp->b3 = (61.0/240 - 103.0/140 * n) * n*n*n;
pp->b3 = 49561.0/161280 * n*n*n*n;
}
void translateTransverseMercator(struct TransverseMercatorParam *pp, int zone,
double lat, double lon, double *ep, double *np) {
double lon2, v, m;
double k4, k6, h3, h5;
double sin_lat = sin(lat);
double cos_lat = cos(lat);
double cos2_lat = cos_lat * cos_lat;
lon -= zone * pp->zw + pp->lon0;
while (unlikely(lon <= -M_PI))
lon += 2*M_PI;
lon2 = lon * lon;
//
v = 1 / sqrt(pp->e2__a2k2 * cos2_lat + pp->ie2__a2k2);
m = ((pp->m6 * cos2_lat + pp->m4) * cos2_lat + pp->m2) * cos2_lat + pp->m1;
k4 = ((pp->q1 * cos2_lat + pp->q2) * cos2_lat + 1.0/4 ) * cos2_lat - 1.0/24;
k6 = ((pp->q3 * cos2_lat + pp->q4) * cos2_lat - 1.0/12) * cos2_lat + 1.0/720;
h3 = (( pp->q6) * cos2_lat + 1.0/3 ) * cos2_lat - 1.0/6;
h5 = ((pp->q7 * cos2_lat + pp->q8) * cos2_lat - 1.0/6 ) * cos2_lat + 1.0/120;
// ( )
*np = pp->m0 + pp->mp * lat
+ (m + v * ((k6 * lon2 + k4) * lon2 + 0.5) * lon2) * cos_lat * sin_lat;
*ep = pp->e0 + pp->zs * zone
+ ( v * ((h5 * lon2 + h3) * lon2 + 1.0) * lon ) * cos_lat;
}
En sortie de la fonction de transformation, nous aurons des coordonnées: les déplacements est et nord (e, n) sont des coordonnées cartésiennes rectangulaires en mètres.

Nous sommes déjà très près de terminer notre algorithme. Il suffit de trouver les coordonnées du pixel (x, y) dans le fichier de la carte. Car les coordonnées des pixels sont également cartésiennes, alors on peut les trouver par transformation affine (e, n) en (x, y). Nous reviendrons sur la recherche des paramètres de la transformation la plus affine un peu plus tard.
struct AffineParam {
double c00, c01, c02;
double c10, c11, c12;
};
void translateAffine(struct AffineParam *app, double e, double n,
double *xp, double *yp) {
*xp = app->c00 + app->c01 * e + app->c02 * n;
*yp = app->c10 + app->c11 * e + app->c12 * n;
}
Et enfin, l'algorithme complet de création de tuiles:
void renderTile(ImagePtr tile, int z, unsigned long x, unsigned long y) {
int i, j;
double wlat, wlon;
ImagePtr srcimg;
double lat, lon;
double e, n;
double x, y;
for (i = 0; i < 256; ++i) {
for (j = 0; j < 256; ++j) {
XYZ_WGS84(x * 256 + j, y * 256 + i, z, &wlat, &wlon);
translateHelmertInv(&Helmert_SK42_WGS84, wlat, wlon, 0, &lat, &lon);
findSrcImg(&srcimg, lat, lon);
translateTransverseMercator(&TM_GaussKruger, srcimg->zone, lat, lon, &e, &n);
translateAffine(&srcimg->affine, e, n, &x, &y);
setPixelColor(tile, j, i, interpolatePixelColor(srcimg, x, y));
}
}
}
Le résultat du travail pour z = 12, y = 1377, x = 2391:

Dans l'algorithme, la fonction de recherche de l'image originale de la carte srcimg à partir des coordonnées géodésiques lat, lon spécifiées dans le SC de la carte n'a pas été décrite. Je pense qu'il n'y aura aucun problème avec celui-ci et le numéro de la zone srcimg-> zone, mais nous nous attarderons à trouver les paramètres de la transformation affine srcimg-> affine plus en détail.
Quelque part sur Internet il y a très longtemps, une telle fonction a été trouvée pour trouver les paramètres d'une transformation affine, je la cite même avec des commentaires originaux:
struct TiePoint {
struct TiePoint *next;
double lon, lat;
double e, n;
double x, y;
};
void setupAffine(struct AffineParam *app, struct TiePoint *plist) {
/*
* :
* x = c00 + c01 * e + c02 * n
* y = c10 + c11 * e + c12 * n
*/
struct TiePoint *pp; /* */
double a11, a12, a13; /* */
double a21, a22, a23; /* 3*3 */
double a31, a32, a33; /* */
double b1, b2, b3; /* */
int m; /* z: m=0 -> z=x, m=1 -> z=y */
double z; /* x, y */
double t; /* */
/* 2- 3 ,
. */
/* */
a11 = a12 = a13 = a22 = a23 = a33 = 0;
for (pp = plist; pp; pp = pp->next) {
a11 += 1;
a12 += pp->e;
a13 += pp->n;
a22 += pp->e * pp->e;
a23 += pp->e * pp->n;
a33 += pp->n * pp->n;
}
/* ( ) */
a21 = a12;
a31 = a13;
a12 /= a11;
a13 /= a11;
a22 -= a21 * a12;
a32 = a23 - a31 * a12;
a23 = a32 / a22;
a33 -= a31 * a13 + a32 * a23;
/* , X Y */
for (m = 0; m < 2; m++) { /* m=0 -> X, m=1 -> Y */
/* */
b1 = b2 = b3 = 0;
for (pp = plist; pp; pp = pp->next) {
z = !m ? pp->x : pp->y;
b1 += z;
b2 += pp->e * z;
b3 += pp->n * z;
}
/* */
b1 /= a11;
b2 = (b2 - a21 * b1) / a22;
b3 = (b3 - a31 * b1 - a32 * b2) / a33;
/* */
t = b2 - a23 * b3;
*(!m ? &app->c00 : &app->c10) = b1 - a12 * t - a13 * b3;
*(!m ? &app->c01 : &app->c11) = t;
*(!m ? &app->c02 : &app->c12) = b3;
}
}
En entrée, au moins trois points d'ancrage doivent être soumis, en sortie, nous obtenons des paramètres prêts à l'emploi. Les points d'ancrage sont des points pour lesquels les coordonnées de pixel (x, y) et les coordonnées de décalage est et nord (e, n) sont connues. Les points d'intersection de la grille kilométrique sur la carte originale peuvent être utilisés comme tels points. Et s'il n'y a pas de grille kilométrique sur la carte? Ensuite, vous pouvez définir des paires (x, y) et (lon, lat), car ces points prennent les points d'intersection des parallèles et des méridiens, ils sont toujours sur la carte. Il ne reste plus qu'à convertir (lon, lat) en (e, n), cela se fait par la fonction de transformation pour la projection, dans notre cas c'est translateTransverseMercator ().
Comme vous pouvez le voir, les points d'ancrage sont nécessaires pour indiquer à l'algorithme la partie de la surface terrestre décrite par le fichier avec l'image de la carte. Étant donné que les deux systèmes de coordonnées étaient cartésiens, quel que soit le nombre de points d'ancrage que nous avons définis et quelle que soit leur distance l'un de l'autre, l'écart sur tout le plan de la carte se situera dans l'erreur de détermination des points d'ancrage. La plupart des erreurs sont que la projection, la référence ou l'ellipsoïde (avec des paramètres pas exactement spécifiés) sont utilisés, par conséquent, les coordonnées (e, n) en sortie ne sont pas obtenues dans le système de coordonnées cartésien, mais dans un système légèrement incurvé par rapport au cartésien. Visuellement, cela peut être visualisé comme une «feuille froissée». Naturellement, l'augmentation du nombre de points d'ancrage ne résout pas ce problème. Le problème peut être résolu en réglant les paramètres de la projection, du datum et de l'ellipsoïde,dans ce cas, un grand nombre de points d'ancrage vous permettra de lisser la "feuille" avec plus de précision et de ne pas rater les zones non lissées.
Et à la fin de l'article, je vous dirai comment utiliser des tuiles prêtes à l'emploi dans OpenLayers et sous quelle forme les préparer pour le programme OsmAnd.
Pour OpenLayers, il vous suffit de mettre les tuiles sur le Web et de les nommer afin de pouvoir mettre en évidence (z, y, x) dans le nom du fichier ou du répertoire, par exemple:
/tiles/topo/12_1377_2391.jpg
ou, mieux encore:
/ tiles / topo /12/1377/2391.jpg
Ensuite, ils peuvent être utilisés comme ceci:
map = new OpenLayers.Map (...);
map.addLayer(new OpenLayers.Layer.XYZ("Topo Maps", "/tiles/topo/${z}_${y}_${x}.jpg", {
isBaseLayer: false, visibility: false,
}));
Pour le programme OsmAnd, il est facile de déterminer le format à partir de tous les fichiers existants avec un ensemble de tuiles. Je vais vous parler tout de suite des résultats. Les tuiles sont emballées dans un fichier de base de données sqlite qui est créé comme ceci:
CREATE TABLE info AS SELECT 99 AS minzoom, 0 AS maxzoom;
CREATE TABLE tiles (x int, y int, z int, s int, image blob, PRIMARY KEY (x,y,z,s));
CREATE INDEX IND on tiles (x,y,z,s);
UPDATE info SET minzoom=$minzoom, maxzoom=$maxzoom
La colonne s est toujours remplie de zéro, ce pour quoi, je n'ai pas compris, l'image est saisie sous la forme binaire d'origine, le format (jpg, png, gif) est perdu, mais OsmAnd le détermine par son contenu. Les tuiles de différents formats peuvent être regroupées dans une seule base de données. Au lieu de $ minzoom et $ maxzoom, il est nécessaire de substituer les limites d'échelle des tuiles entrées dans la base. Le fichier de base de données complété, par exemple, Topo.sqlitedb, est transféré sur un smartphone ou une tablette dans le répertoire osmand / tiles. Redémarrez OsmAnd, dans Menu -> "Configurer la carte" -> "Top Layer" une nouvelle option "Topo" apparaîtra - c'est une carte avec nos nouvelles tuiles.