🐷 🥖 🐇 Y a-t-il un parallélisme dans un algorithme arbitraire et comment l'utiliser de la meilleure façon 👨‍👧‍👦 🐣 🙍🏽

La parallélisation du traitement des données est actuellement utilisée principalement pour réduire le temps de calcul en traitant simultanément des données par parties sur de nombreux appareils informatiques différents, puis en combinant les résultats. L'exécution parallèle permet de «contourner» la loi fondamentale formulée par Lord Rayleigh en 1871, selon laquelle (appliquée à la dissipation thermique des processeurs) leur puissance de dissipation thermique est proportionnelle à la quatrième puissance de la fréquence d'horloge du processeur (doubler la fréquence augmente la dissipation thermique 16 fois) et la remplacer par une le nombre d'ordinateurs parallèles - tout en maintenant la fréquence d'horloge). Rien n'est donné gratuitement - le problème de révéler (généralement caché pour l'observateur non initié, [1]) le potentiel de parallélisme dans les algorithmes n'est pas à la surface,et l'efficacité de son utilisation (parallélisme) - encore plus.

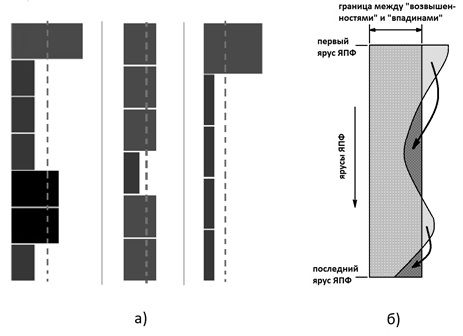
Vous trouverez ci-dessous une illustration du processus de détection de parallélisme pour le cas le plus simple de l'évaluation de l'expression axb + a / c (a, b, c - données d'entrée).

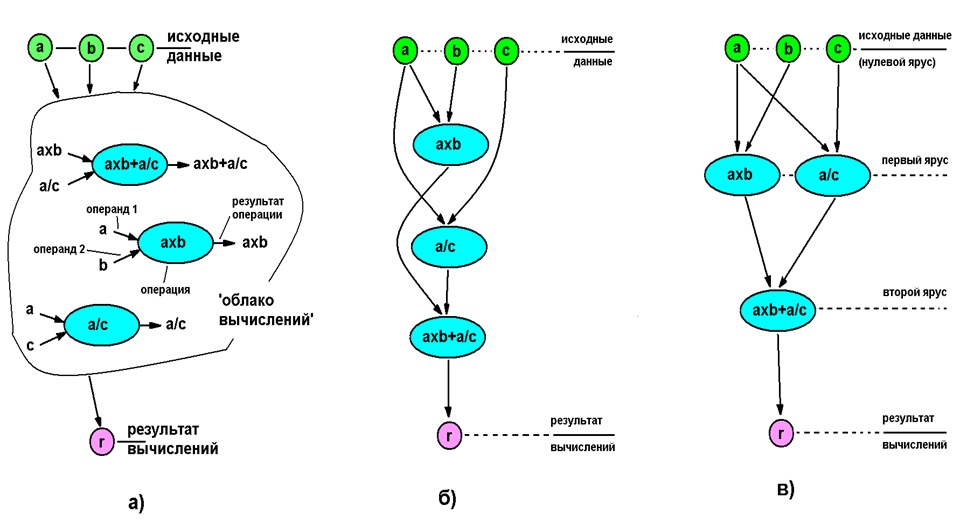
a) - "nuage d'opérateurs" (la séquence d'exécution n'est pas définie), b) - exécution complètement séquentielle, non définie), b) - exécution complètement séquentielle, c) - exécution parallèle

, . ( ) ( – ., ). .1 “ ”, ( ) .

(- ), . , . () . NP- [2], ( ) ( -). , “ ” (Data Science).

AlgoWiki [3].

, , c ILP (Instruction-Level Parallelism, , EPIC (Explicitly Parallel Instruction Computing, ). , .

() ( , ). (). “ - ”, ( ) , – () ). , (- ).

( ) - (), [4]. ( ).

( ) O(N2) , N – ( ), ( ) . ( ). .. , . , .

, , .

. ax2+bx+c=0.

La figure montre la forme parallèle à plusieurs niveaux de l'algorithme pour résoudre l'équation quadratique complète en nombres réels sous la forme canonique (les numéros des niveaux du LPF sont situés à droite) — - - ( )

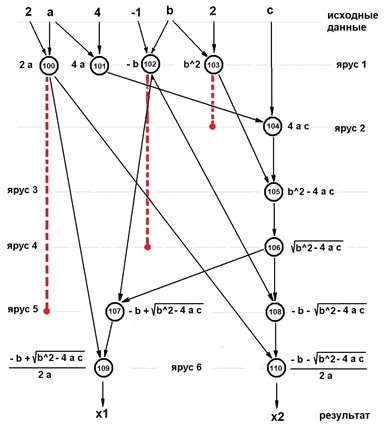
( “ ”, 6 4- ). ( ) – 1- 4, 2,3,4 - 5- 6 . , ( ) ( ) ! – ( ).

( ) , - D-F SPF@home. http://vbakanov.ru/dataflow/content/installdf.exe http://vbakanov.ru/spf@home/content/installspf.exe ( - http://vbakanov.ru/dataflow/dataflow.htm http://vbakanov.ru/spf@home/spf@home.htm).

La figure montre le diagramme du complexe instrumental (* .set et * .gv - le fichier programme et le fichier du graphe d'information du programme analysé, respectivement, * .mvr, * .med - fichiers des métriques des sommets et des arcs du graphe d'algorithme, respectivement, * .cls, * .ops - fichiers de paramètres de calculatrices et d'opérateurs de programme, respectivement, * .lua - un fichier texte en langage Lua, contenant des méthodes de réorganisation — - (*.set *.gv – , *.mvr, *.med – , *.cls, *.ops – , *.lua – Lua,

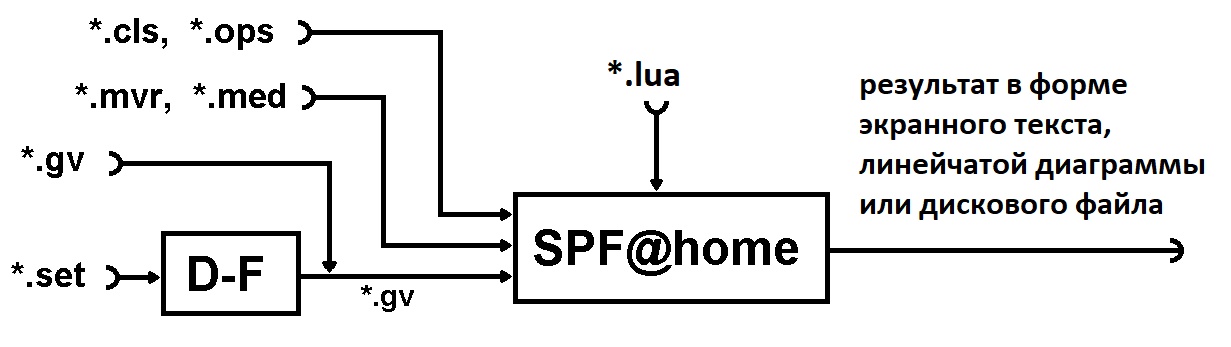
(set-) – gv- ( “ - ”, ( ) , – () ). , (- ).

() . “” .

Lua (Lua ANSI C, , - , ).

++, GUI Win’32- ( ) GIT-. ( ).

(Lua- “” API- SPF@home).

( D-F SPF@home ).

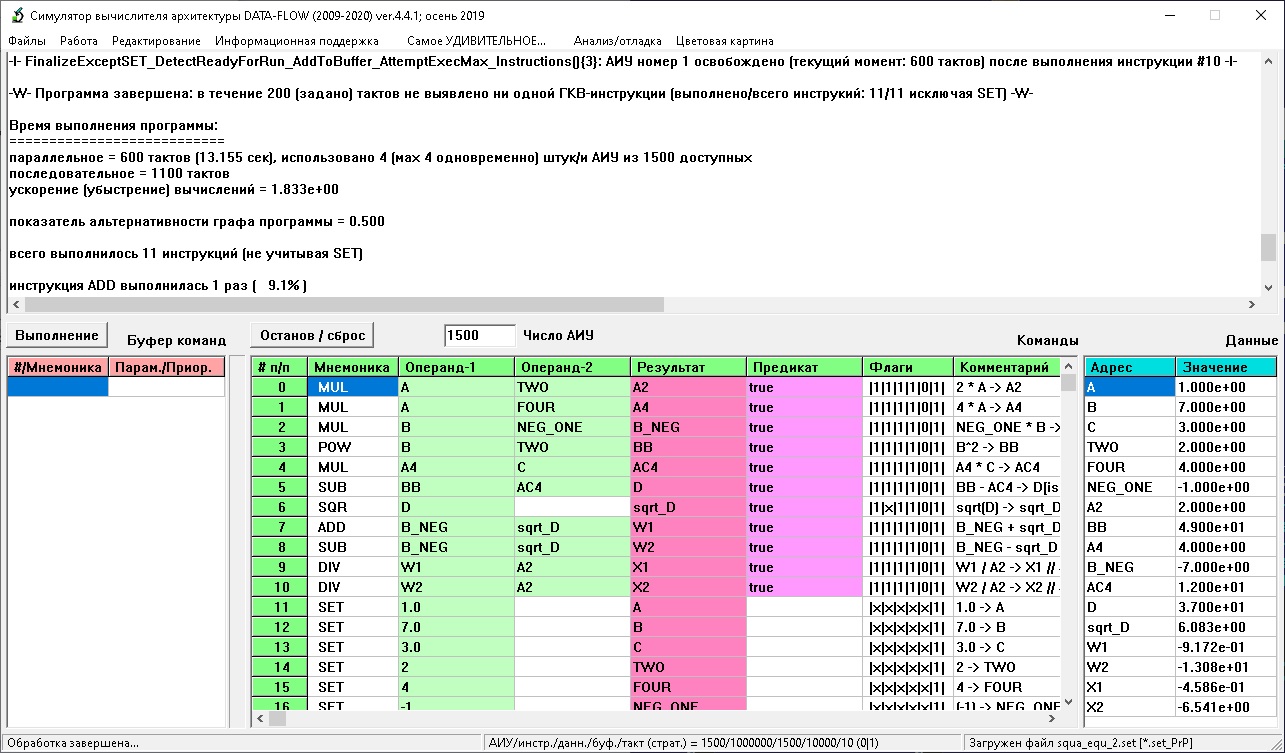
D-F (Data-Flow) , . 1 “Data-Flow” ( ), (), ; . - , , , “” . D-F , .

D-F , , . ( set- D-F, ):

, . D-F , - SPF@home. SPF@home gv- ( ), , Lua- ( API- , ):

CreateTiersByEdges("EdgesData.gv")  --     EdgesData.gv 
--    “”
-- CreateTiersByEdges_Bottom("EdgesData.gv")  --     EdgesData.gv 
--    “”
--
OpsOnTiers={} --   1D- OpsOnTiers 
for iTier=1,GetCountTiers() do --   
   OpsOnTiers[iTier]={} --  iTier-  2D- OpsOnTiers
   for nOp=1,GetCountOpsOnTier(iTier) do --       iTier  
      OpsOnTiers[iTier][nOp]=GetOpByNumbOnTier(nOp,iTier) --    nOp
end end --   for  iTier  for  nOp

gv- mvr med-, cls ops- . ( “-”, ) . , .

SPF@home “ ” , / ( ). med-.

, c ILP (Instruction-Level Parallelism, ), SPF@home .

.. Lua-, . ( ) :

I. “” ( ).

II. ( ).

III. .

( ) ; ( ).

, (, ) , , ( – ).

1) ( ) .

2) .

- . ( , , , ). “” API- “” ( , ).

“” ( ) ( ). “” “” ( ; “” ””).

( ) - “ ”, , “” . ( ). “” Windows- WinExec, ShellExecute CreateProcess, (, METIS -), Lua.

.6 ( ) “Bulldozer”, , “” “”.

En figue. sont représentés des diagrammes à barres des largeurs des niveaux d'IPF réels à partir de copies d'écran lorsque le système SPF @ home fonctionne (la moyenne arithmétique des largeurs est indiquée par une ligne pointillée, a) et le schéma symbolique de la méthode «Bulldozer» - b) — . SPF@home (- , a) “Bulldozer” - )

, ( 1,5-2 ) , (- ).

.. ( Lua) (., c , , .).

SPF@home ( ) . , . ( ) ( , , ). , .

, ( ) .

1. .., .. . — .: -, 2002. — 608 c.
2. ., . . : — , , 2012. — 420 c.
3. AlgoWiki. . URL: http://algowiki-project.org ( 31.07.2020).
4. .. . . — .: -, 2018. — 390 .
5. Roberto Ierusalimschy. Programming in Lua. Third Edition. PUC-Rio, Brasil, Rio de Janeiro, 2013. — 348 p.

Y a-t-il un parallélisme dans un algorithme arbitraire et comment l'utiliser de la meilleure façon

More articles: