De quoi parle le post?
Ce matériel fournit une brève description du problème dans la théorie des automates numériques et explique l'un des moyens de résoudre ce problème, qui a été trouvé en essayant d'automatiser le processus de construction d'automates numériques.
introduction
La machine automatique est un système de mécanismes, de dispositifs, dans lequel les processus de réception, de conversion, de transfert d'énergie, de matériaux et d'informations sont entièrement automatisés.
Le terme «automate» est principalement utilisé sous deux aspects:
technique;
mathématique.
Dans l'approche mathématique, un automate est compris comme un modèle mathématique, qui doit avoir des entrées, des états internes et des sorties. Les détails de la structure de l'appareil ne sont ni pris en compte ni pris en compte.
Dans l'approche technique, un automate est entendu comme un appareil tout à fait réel, par exemple un appareil téléphonique, un distributeur automatique, etc. Dans ce cas, bien entendu, les détails de la structure interne du dispositif sont connus.
Du point de vue des signaux, un automate numérique (DA) est un système qui peut recevoir des signaux d'entrée, sous leur influence, passer d'un état à un autre, le sauvegarder jusqu'à l'arrivée du signal d'entrée suivant et émettre des signaux de sortie.
Cet article traite des signaux numériques et de la logique binaire basés sur des éléments logiques.
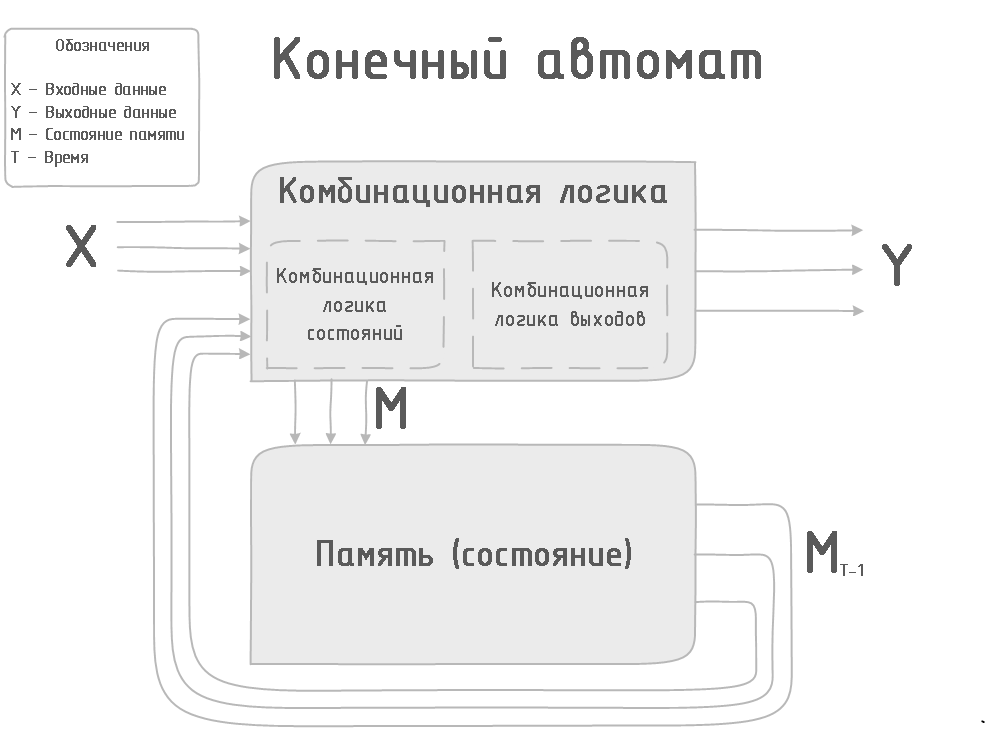
. , , , , .
— .
(). , , , , . .
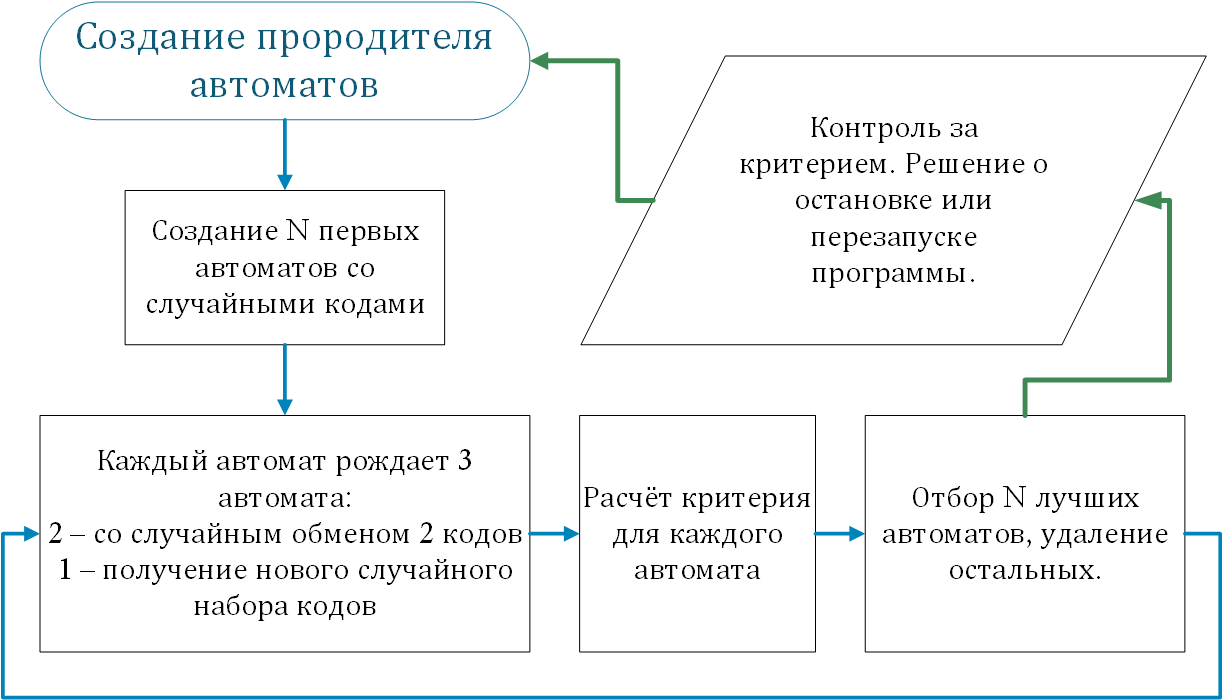
-- . :
1) , .
2) -- .
3) . :
, S -- , ceil -- , .
4) . . , .
5) -.
6) . -, .
7) .
8) .
-- , .
. . (, , ). . -- . <<>>, <<>>. .
(M) (S).
:
(V) (S) (C), :
(A) :
, . .
.
6720. .
( ), 0( ) 1( ).
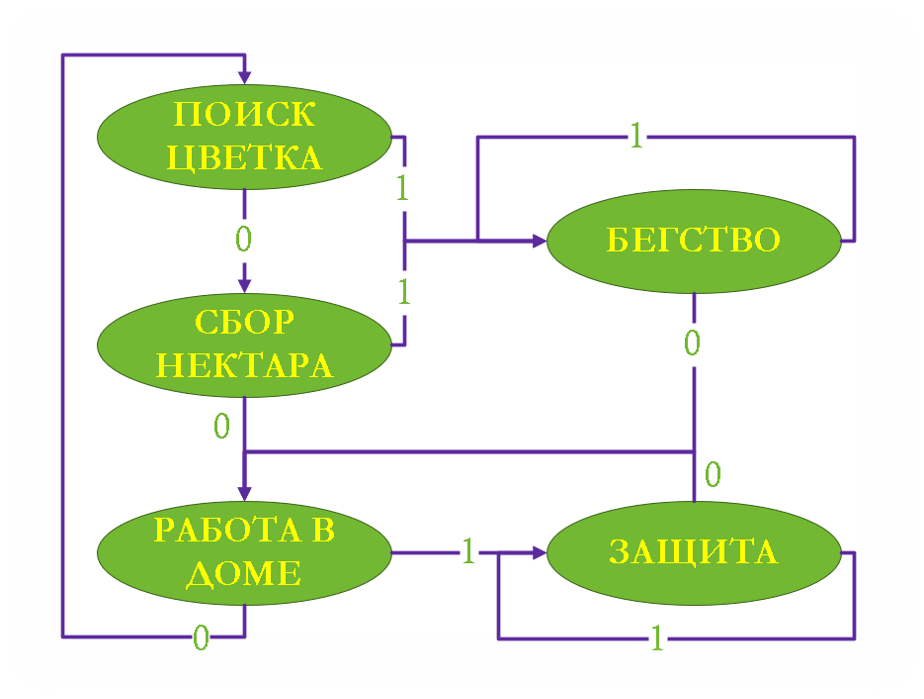
:
: 5
: ceil(log2(5)) = 3
: 1
:
(V) X(X<S!) . -- . c S! .
, -- 0 1 .
Pour les automates complexes, où le dénombrement prend beaucoup de temps, une solution efficace serait d'appliquer un algorithme génétique, cela ne trouve pas forcément le meilleur résultat, mais cela vous permettra de trouver rapidement une solution proche de lui.