On pense généralement qu'une mesure quantique affecte l'objet mesuré - elle passe d'un état indéfini à un certain état, comme en physique quantique une superposition d'états "s'effondre" en un seul état propre. Cependant, peu de gens pensent que la mesure peut également détruire des informations quantiques.
Imaginez-vous dans la peau d'un scientifique essayant de comprendre la réalité à un niveau fondamental. Comment géreriez-vous ce problème? Vous essaieriez de décomposer la matière en minuscules composants plus faciles à étudier. Vous concevriez des expériences pour tester et mesurer les propriétés de ces minuscules particules subatomiques dans divers états. Si vous étiez vraiment intelligent, vous essaieriez d'utiliser les propriétés que vous avez mesurées pour comprendre les lois de l'univers.
Vous pourriez bien décider qu'avec suffisamment de mesures, ou suffisamment d'expériences, vous pouvez trouver tout ce que vous voulez sur n'importe quelle particule (ou groupe de particules) dans tout l'univers. Des attentes similaires étaient courantes chez les scientifiques à l'aube du 20e siècle. Mais il s'est avéré que l'univers quantique a d'autres propositions pour nous. Certaines mesures annulent complètement les informations que vous avez reçues lors des mesures précédentes. Apparemment, le fait de mesurer détruit les informations. Et c'est ainsi que nous l'avons découvert.

Certaines opérations mathématiques, telles que l'addition ou la multiplication, ne dépendent pas de l'ordre des actions - elles sont commutatives. Si l'ordre des opérations est important et que le résultat en dépend, alors les opérations sont dites non commutatives. Dans le monde de la physique, c'est très important.
En théorie, l'histoire commence par une idée mathématique simple: le concept de commutativité. La Commutativité, c'est quand vous pouvez réorganiser les pièces par endroits sans changer le résultat. L'addition est commutative: 2 + 3 = 3 + 2. Il en est de même pour la multiplication: 2 × 3 = 3 × 2. La soustraction n'est pas commutative: 2 - 3 ≠ 3 - 2; vous devez ajouter un signe moins à droite pour que l'expression devienne vraie. La division n'est pas non plus commutative, et avec elle tout est un peu plus compliqué: 2 ÷ 3 ≠ 3 ÷ 2; l'une des parties doit être inversée pour la rendre égale à l'autre.
En physique, la commutabilité se réfère non seulement aux opérations mathématiques, mais aussi à la manipulation physique ou à la mesure. Un exemple simple: les rotations. Nous pouvons prendre un objet qui est différent dans les trois dimensions - par exemple, un téléphone portable - et faire deux rotations l'une après l'autre:
- en tenant l'objet devant vous, faites-le pivoter de 90 ° dans le sens antihoraire par rapport à l'axe dirigé vers vous;
- faites pivoter le même objet de 90 ° dans le sens des aiguilles d'une montre autour de l'axe vertical.
Il peut en surprendre certains que l'ordre dans lequel ces rotations sont effectuées compte.

Le téléphone précédent de l'auteur, de l'époque avant les smartphones, illustre la non-commutativité des rotations dans l'espace tridimensionnel. Les rangées du haut et du bas, de gauche à droite, commencent à la même position. En haut, après une rotation de 90 ° dans le sens antihoraire dans le plan de la photographie, une rotation de 90 ° dans le sens horaire autour de l'axe vertical suit. En bas, les deux mêmes tours sont effectués dans un ordre différent. La non-commutativité des rotations est évidente.
L'idée de non-commutativité apparaît même dans le monde de la physique classique, mais son application la plus célèbre concerne le monde quantique sous la forme du principe d'incertitude de Heisenberg... Dans notre monde classique, nous pouvons mesurer de nombreuses propriétés d'un objet à un moment donné. Placez un objet sur la balance et mesurez sa masse [poids / env. par.]. Fixez-y un capteur de mouvement et mesurez son élan. Tirez dessus avec un laser et mesurez son emplacement. Envoyez-le au calorimètre et mesurez son énergie. Démarrez le chronomètre pendant que l'objet vacille et obtenez la période d'oscillation.
Dans l'univers quantique, bon nombre de ces mesures sont valides, mais seulement au moment où vous les faites - et pas pour toujours. Le fait est que certaines propriétés quantiques que vous pouvez mesurer - des paires de quantités appelées variables conjuguées - sont liées les unes aux autres. Si vous mesurez l'élan avec une certaine précision, vous ne pouvez pas connaître l'emplacement d'une particule plus précisément qu'avec une certaine erreur - même si vous aviez précédemment mesuré cet emplacement avec beaucoup plus de précision.
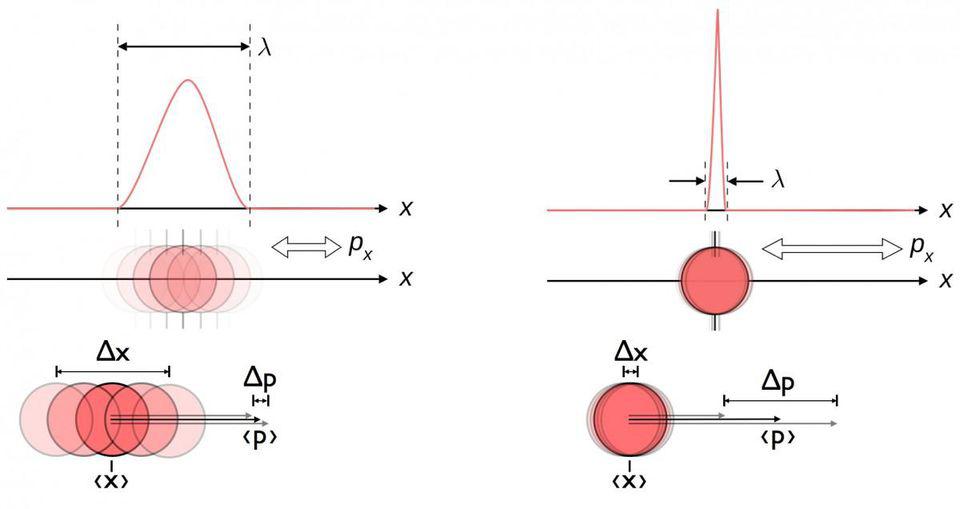
L'incertitude inhérente au monde quantique entre l'emplacement et l'élan. Mieux vous connaissez l'emplacement d'une particule, moins vous connaissez son élan - et vice versa. L'emplacement et le moment sont mieux décrits par une fonction d'onde probabiliste que par une seule valeur.
Beaucoup ont eu du mal à accepter le principe d'incertitude, et pourtant l'univers semble le soutenir. Cela s'applique également à d'autres paires de variables conjuguées:
- localisation (Δx) et impulsion (Δp),
- énergie (ΔE) et temps (Δt),
- potentiel électrique, ou tension (Δφ) et charge électrique libre (Δq),
- moment angulaire (ΔL) et orientation, ou position angulaire (Δθ).
Cependant, si vous avez vraiment besoin de démontrer une nécessité physique, vous devez obtenir des preuves expérimentales pour la soutenir. Il ne suffit pas de dire simplement «Je ne sais pas à quel point mes mesures sont précises». Vous devez trouver un moyen de montrer que les informations que vous avez reçues lors de mesures précédentes avec une certaine précision ont été détruites par des mesures ultérieures.
Et en 1921, le physicien Otto Stern a proposé une manière ingénieuse de tester cela.

Les particules individuelles et composites peuvent avoir un moment angulaire orbital et intrinsèque (spin). Lorsque ces particules ont une charge électrique intrinsèque ou intrinsèque, un moment magnétique apparaît qui les fait dévier d'une certaine quantité en présence d'un champ magnétique.
Disons que vous avez une particule quantique - un électron, un proton, un noyau composite (un objet composé de protons et de neutrons liés), ou même un atome neutre avec un noyau et des électrons tournant autour de lui. Un tel objet possède plusieurs propriétés quantiques qui lui sont inhérentes: masse, charge électrique, etc. En théorie, il devrait également avoir un moment cinétique - non seulement parce qu'il tourne autour d'autres particules (ou d'autres particules tournent autour de lui), mais aussi un moment angulaire interne inhérent. Cette propriété quantique d'un objet est appelée spin [to spin (anglais) - to rotate / approx. per.], par analogie avec un sommet tournant autour de son propre axe.
Si vous imaginez un sommet, vous pouvez immédiatement trouver deux façons de le faire pivoter:
- dans le sens horaire autour de l'axe vertical,
- ou dans le sens antihoraire.
Vivant dans un monde sans gravité (et sans directions privilégiées - dont le rôle, dans notre cas, est joué par la direction vers le centre de la Terre), on pourrait imaginer sa rotation dans le sens horaire ou antihoraire autour de n'importe quel axe dans les trois dimensions. C'est notre prémisse: l'idée que les particules ont un spin, un moment angulaire interne. Bien qu'en 1921, il y ait encore plusieurs années avant que George Eugene Uhlenbeck et Samuel Abraham Goudsmit aient formulé leur hypothèse du spin de l'électron, cette idée était encore présente dans la «vieille théorie quantique» de Bohr et Sommerfeld.

La trajectoire d'une particule quantique en rotation traversant un champ magnétique est affectée par son moment magnétique associé à son spin. En théorie quantique, cela signifie que le spin doit être discret.
Comment mesurer le spin des particules quantiques? Comment déterminer si le spin est une quantité continue qui peut prendre n'importe quelle valeur à la manière des paramètres classiques, ou est-il intrinsèquement quantique et discret?
Stern a deviné que si nous prenons un champ magnétique perpendiculaire à la direction du mouvement d'une particule chargée avec un spin, le champ agira sur la trajectoire du mouvement en fonction du moment magnétique associé au spin. Une particule sans spin ne sera pas affectée, mais une particule avec un spin déviera dans la direction du champ magnétique.
Si le spin est discret, c'est-à-dire quantifié, toutes les particules se déplaçant à la même vitesse doivent être au même endroit. Si le spin est classique et continu, les particules peuvent être n'importe où.

Un faisceau de particules traversant un aimant peut donner des résultats quantiques / discrets (5) pour le moment cinétique des particules, ou classique / continu (4). L'expérience de Stern-Gerlach a démontré l'existence de plusieurs phénomènes quantiques importants.
En 1922, le physicien Walter Gerlacha organisé un test des idées de Stern en développant une expérience. Gerlach a commencé avec un électroaimant, à travers lequel voyage un faisceau d'atomes d'argent, qui peut être facilement accéléré à des vitesses égales. Lorsque l'électroaimant a été désactivé, tous les atomes d'argent ont frappé au même endroit sur le détecteur de l'autre côté de l'aimant. Lorsque l'aimant a été activé, le faisceau s'est divisé en deux parties - la moitié des atomes a changé de trajectoire, déviant dans un sens, la moitié dans l'autre. On sait aujourd'hui que ce comportement correspond à la présence de spins +1/2 et -1/2 dirigés parallèles ou antiparallèles aux lignes de champ magnétique.
Cette première expérience a suffi à prouver l'existence du spin, qui est quantifié en valeurs discrètes. Cependant, la capacité de la mécanique quantique à détruire les informations précédemment obtenues a été démontrée. Lorsque les atomes d'argent traversent l'appareil de Stern-Gerlach avec le champ magnétique activé, le faisceau d'atomes est divisé en deux, conformément aux spins des particules.
D'accord - et si nous passons l'une des moitiés du faisceau à travers un autre appareil Stern-Gerlach?

Si vous projetez des particules à travers l'appareil de Stern-Gerlach, le champ magnétique divisera leur faisceau en deux parties, conformément aux options de rotation possibles. Si le deuxième appareil de Stern-Gerlach est placé sur le trajet de l'une des moitiés du faisceau, la division ne se produira plus, puisque cette propriété quantique des particules a déjà été déterminée.
La réponse peut vous surprendre: tout dépend de la direction dans laquelle l'aimant est orienté. Si le premier appareil de Stern-Gerlach était orienté, par exemple, le long de l'axe des x, alors certaines des particules iront dans la direction + x, et d'autres - dans la direction –x. Concentrons-nous sur le premier. Si vous les passez à travers un autre aimant, orienté le long de l'axe x, les particules ne se sépareront pas - elles resteront toutes orientées dans la direction + x.
Mais si vous orientez le deuxième champ magnétique le long de l'axe y, le résultat peut vous surprendre. Maintenant, le faisceau de particules, initialement orienté dans la direction + x, se divisera le long de l'axe y: la moitié ira dans la direction + y et l'autre dans la direction –y.
Puis vient le moment critique: que se passe-t-il si nous nous concentrons uniquement sur les particules + y, et que nous les passons à nouveau à travers un champ magnétique orienté selon l'axe x?
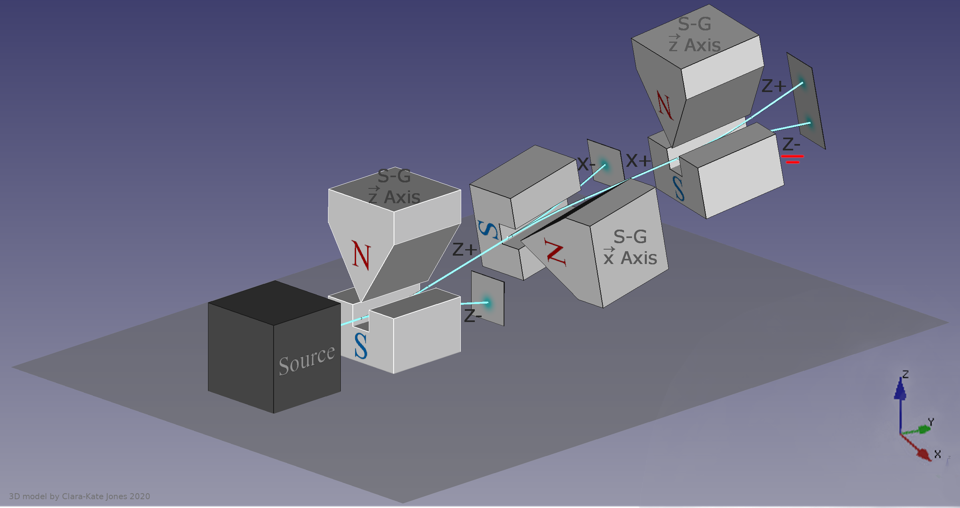
Si vous passez une fois un ensemble de particules à travers l'appareil de Stern-Gerlach, elles se sépareront en fonction de leur rotation. Si vous les passez à travers un deuxième aimant perpendiculaire, ils se séparent dans une nouvelle direction. Si vous utilisez un troisième aimant parallèle au premier, ils se sépareront à nouveau - ce qui signifie que les informations précédemment déterminées sont redevenues aléatoires en raison de la mesure la plus récente.
Ils vont à nouveau, comme la première fois, se diviser le long des directions + x et –x. En les faisant passer à travers le deuxième aimant, orienté perpendiculairement, vous avez détruit les informations obtenues lors de la première mesure. Aujourd'hui, nous comprenons que les directions x, y et z ne font pas la navette entre elles. Une mesure quantique d'une variable d'un type détruit toutes les informations précédentes sur ses variables conjuguées.

Plusieurs appareils successifs divisant les particules quantiques selon l'un des axes selon leur spin les diviseront le long de la perpendiculaire à la direction précédente, mais ne se diviseront pas selon la même direction.
L'expérience de Stern-Gerlach a une conséquence durable. En 1927, il a été montré que la division se produit même dans les atomes d'hydrogène, ce qui indique qu'ils ont un moment magnétique non nul. Les noyaux atomiques ont un moment angulaire quantique inhérent, et ils se fissent également dans l'appareil de Stern-Gerlach. En modifiant le champ magnétique au fil du temps, les scientifiques ont compris comment faire prendre un moment magnétique dans un état ou un autre. Il s'est avéré possible d'induire des transitions entre les états en modifiant le champ dans le temps. Ce fut la naissance de la résonance magnétique, qui est maintenant omniprésente dans les appareils d'IRM, et a finalement conduit à l'horloge atomique.

- . . . 1937 , , .
Il semblerait que l'acte de mesure et d'observation ne devrait pas influencer le résultat de l'expérience. L'idée que l'observation d'un système modifie ses propriétés semble absurde. Mais dans l'univers quantique, cela ne se produit pas seulement - cela a été démontré avant même que la théorie ne soit complètement formée. La mesure du spin d'une particule dans une direction détruit les informations précédemment obtenues sur les deux autres directions. Même si vous les avez mesurés auparavant et que vous les connaissez exactement, la nouvelle dimension efface fondamentalement (aléatoirement) toutes les informations précédemment obtenues.
À de nombreux physiciens qui ont entendu la célèbre déclaration d'Einstein selon laquelle " Dieu ne joue pas aux dés avec l'univers«Cette expérience doit d'abord venir à l'esprit comme un contre-exemple. Peu importe la façon dont vous pensez comprendre la réalité. Peu importe la précision et la précision avec laquelle vous la mesurez de différentes manières. Toute mesure aléatoirement intrinsèquement une information. La nouvelle dimension détruit les anciennes informations.Tout ce qui est nécessaire pour le prouver est un aimant et des particules.