Se souvenir de l'algorithme de Dijkstra
L'algorithme de Dijkstra est l'un des algorithmes de théorie des graphes les plus populaires. Il est utilisé pour trouver le chemin le plus court entre les nœuds sur un graphe orienté. Nous commençons par le nœud source et les longueurs de bord connues entre les nœuds.
Tout d'abord, nous attribuons la distance de la source à tous les nœuds. Le nœud s obtient la valeur 0 car c'est la source; les autres obtiennent des valeurs ∞ pour commencer.
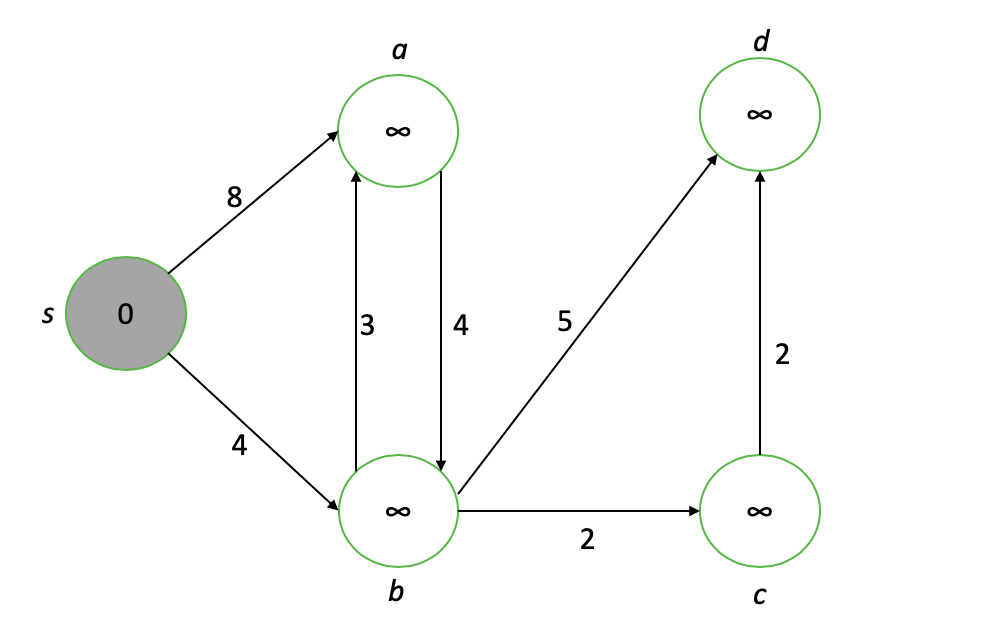
Notre nœud d'intérêt est le nœud brut avec la valeur la plus faible (indiquée en gris), c'est-à-dire s. Tout d'abord, nous "affaiblissons" chaque sommet adjacent à notre nœud d'intérêt, en mettant à jour leurs valeurs au minimum de leur valeur actuelle ou de la valeur du nœud d'intérêt plus la longueur du bord de connexion ...
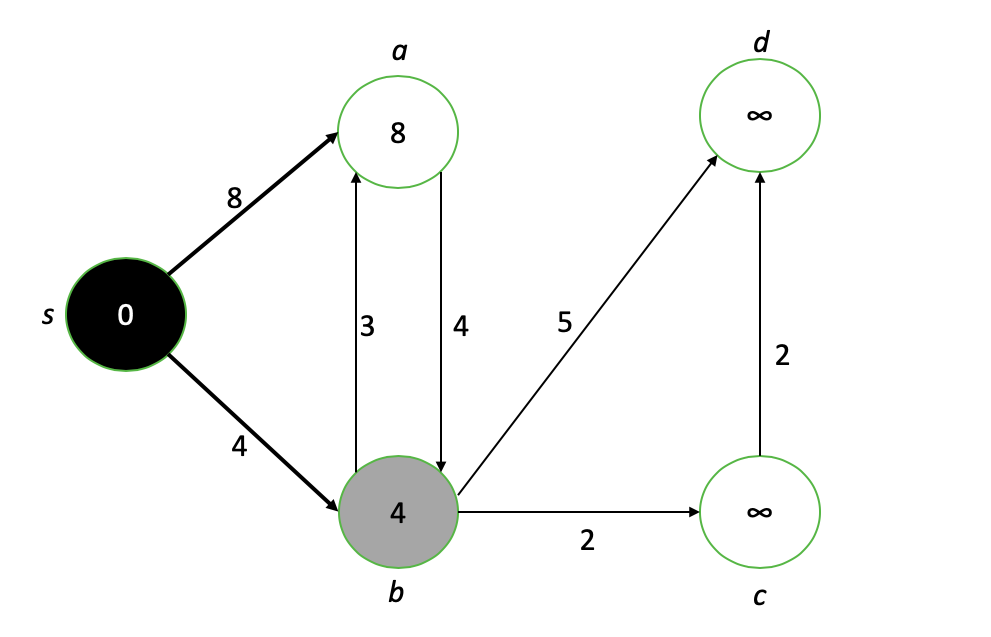
Le nœud s est maintenant terminé (noir) et ses voisins a et b ont pris de nouvelles valeurs. Le nouveau nœud d'intérêt est b, nous répétons donc le processus d'affaiblissement des voisins de b et de finalisation de la valeur de chemin la plus courte pour b.

Après avoir parcouru chaque nœud, nous obtiendrons enfin un graphique montrant la longueur de chemin la plus courte de la source à chaque nœud.
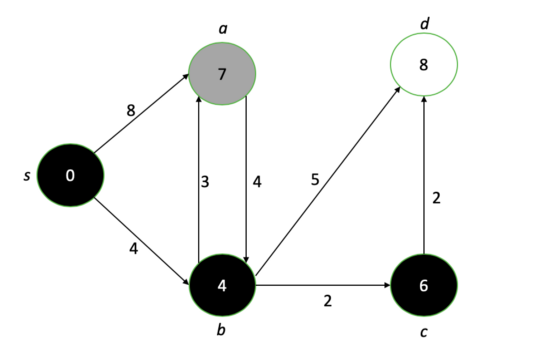


Notre diagramme final après avoir exécuté l'algorithme de Dijkstra. Les nombres à chaque nœud représentent la distance la plus courte possible du nœud source.
Conceptualisation des images de labyrinthe

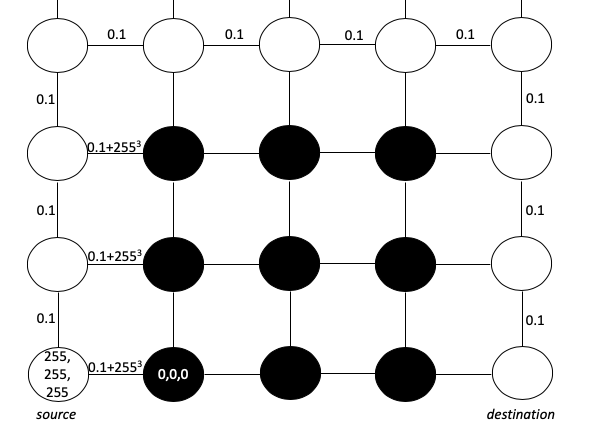
On peut considérer une image comme une matrice de pixels. Chaque pixel (pour plus de simplicité) a une valeur RVB 0,0,0 (noir) ou 255,255,255 (blanc). Notre objectif est de créer le chemin le plus court qui commence sur le blanc et ne mène pas aux bordures noires. Pour représenter cet objectif, nous pouvons traiter chaque pixel comme un nœud et dessiner des bords entre des pixels adjacents avec des longueurs de bord basées sur la différence de valeurs RVB. Nous utiliserons la formule de distance carrée euclidienne et ajouterons 0,1 pour nous assurer qu'il n'y a pas de longueur de chemin 0 - (exigence de l'algorithme de Dijkstra):
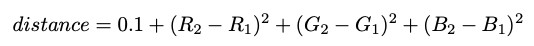
Cette formule rend la distance d'intersection à travers la limite du labyrinthe excessivement grande. Comme nous pouvons le voir, le chemin le plus court de la source à la destination contournera clairement la barrière et non la traversera.
la mise en oeuvre
Nous pouvons utiliser OpenCV, une bibliothèque de vision par ordinateur populaire pour Python, pour extraire les valeurs de pixels et afficher nos images de labyrinthe. Définissons également les coordonnées de nos emplacements de début et de fin en ajoutant des points à notre labyrinthe
import cv2
import matplotlib.pyplot as plt
import numpy as np
img = cv2.imread('maze.png') # read an image from a file using
cv2.circle(img,(5,220), 3, (255,0,0), -1) # add a circle at (5, 220)
cv2.circle(img, (25,5), 3, (0,0,255), -1) # add a circle at (5,5)
plt.figure(figsize=(7,7))
plt.imshow(img) # show the image
plt.show()
Nous créons une classe Vertex qui nous aidera à suivre les coordonnées. Nous voulons également suivre le nœud parent afin de pouvoir restaurer le chemin complet dès que nous trouvons les valeurs de distance.
class Vertex:
def __init__(self,x_coord,y_coord):
self.x=x_coord
self.y=y_coord
self.d=float('inf') #current distance from source node
self.parent_x=None
self.parent_y=None
self.processed=False
self.index_in_queue=NoneNous devons créer une matrice de sommets représentant la disposition bidimensionnelle des pixels dans l'image. Ce sera la base de l'algorithme de Dijkstra. Nous conservons également une file d'attente de faible priorité pour suivre les nœuds non traités.
def find_shortest_path(img,src,dst):
pq=[] #min-heap priority queue
imagerows,imagecols=img.shape[0],img.shape[1]
matrix = np.full((imagerows, imagecols), None)
#access matrix elements by matrix[row][col]
#fill matrix with vertices
for r in range(imagerows):
for c in range(imagecols):
matrix[r][c]=Vertex(c,r)
matrix[r][c].index_in_queue=len(pq)
pq.append(matrix[r][c])
#set source distance value to 0
matrix[source_y][source_x].d=0
#maintain min-heap invariant (minimum d Vertex at list index 0)
pq = bubble_up(pq, matrix[source_y][source_x].index_in_queue)Nous avons besoin de quelques fonctions d'assistance pour aider à trouver les arêtes et la longueur des arêtes entre les sommets:
#Implement euclidean squared distance formula
def get_distance(img,u,v):
return 0.1 + (float(img[v][0])-float(img[u][0]))**2+(float(img[v][1])-float(img[u][1]))**2+(float(img[v][2])-float(img[u][2]))**2
#Return neighbor directly above, below, right, and left
def get_neighbors(mat,r,c):
shape=mat.shape
neighbors=[]
#ensure neighbors are within image boundaries
if r > 0 and not mat[r-1][c].processed:
neighbors.append(mat[r-1][c])
if r < shape[0] - 1 and not mat[r+1][c].processed:
neighbors.append(mat[r+1][c])
if c > 0 and not mat[r][c-1].processed:
neighbors.append(mat[r][c-1])
if c < shape[1] - 1 and not mat[r][c+1].processed:
neighbors.append(mat[r][c+1])
return neighborsMaintenant, nous pouvons implémenter l'algorithme de Dijkstra et attribuer des valeurs de distance (d) à tous les sommets de pixels dans l'image du labyrinthe:
while len(pq) > 0:
u=pq[0] #smallest-value unprocessed node
#remove node of interest from the queue
pq[0]=pq[-1]
pq[0].index_in_queue=0
pq.pop()
pq=bubble_down(pq,0) #min-heap function, see source code
u.processed=True
neighbors = get_neighbors(matrix,u.y,u.x)
for v in neighbors:
dist=get_distance(img,(u.y,u.x),(v.y,v.x))
if u.d + dist < v.d:
v.d = u.d+dist
v.parent_x=u.x #keep track of the shortest path
v.parent_y=u.y
idx=v.index_in_queue
pq=bubble_down(pq,idx)
pq=bubble_up(pq,idx)Maintenant, nous pouvons appeler la fonction de chemin le plus court et dessiner la solution dans notre labyrinthe:
img = cv2.imread('maze.png') # read an image from a file using opencv (cv2) library
p = find_shortest_path(img, (25,5), (5,220))
drawPath(img,p)
plt.figure(figsize=(7,7))
plt.imshow(img) # show the image on the screen
plt.show()

Essayons d'autres labyrinthes de partout sur Internet.

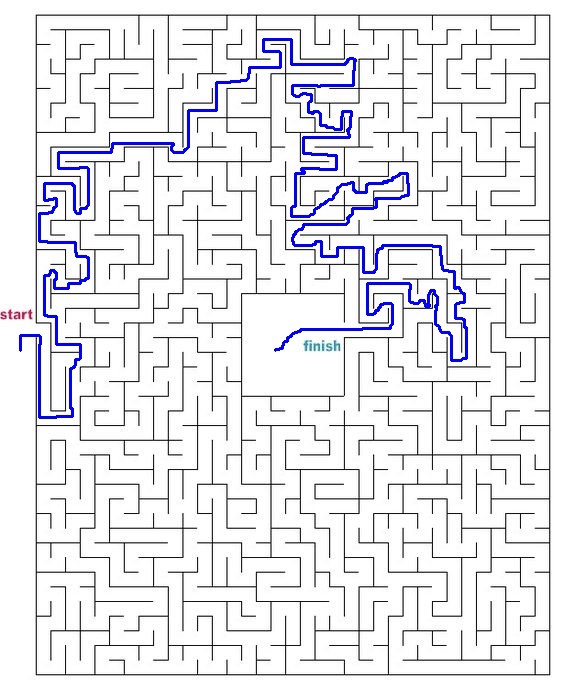


Le code source complet est disponible sur GitHub ici .
Suite: Projet d'apprentissage Python: 40 lignes d'interface de code (partie 2)

Apprenez en détail comment obtenir une profession de premier plan à partir de zéro ou passer au niveau supérieur en compétences et salaires en suivant nos cours en ligne SkillFactory payés:
- Cours d'apprentissage automatique (12 semaines)
- Apprendre la science des données à partir de zéro (12 mois)
- Profession analytique avec n'importe quel niveau de départ (9 mois)
- «Python -» (9 )