Je me souviens avoir vu la photo ci-dessus sur Flickr un jour et m'être brisé le cerveau en essayant de comprendre ce qui n'allait pas. Le fait était que l'hélice tournait au moment où le capteur de mouvement de la caméra "lisait des lectures", c'est-à-dire que pendant l'exposition de la caméra, il y avait un certain mouvement. Cela vaut vraiment la peine d'y réfléchir, réfléchissons-y ensemble.
De nombreux appareils photo numériques utilisent aujourd'hui un capteur CMOS comme dispositif de «détection», également appelé capteur de pixels actifs., qui fonctionne en accumulant la charge électronique lorsque la lumière le frappe. Après un certain temps - temps d'exposition - la charge est transférée ligne par ligne vers l'appareil photo pour un traitement ultérieur. La caméra scanne ensuite l'image, en conservant les lignes de pixels ligne par ligne. L'image sera déformée s'il y a un mouvement pendant la prise de vue. À titre d'illustration, imaginez tirer sur une hélice en rotation. Dans les animations ci-dessous, la ligne rouge correspond à la position de lecture actuelle et l'hélice continue de tourner pendant la lecture. La partie sous la ligne rouge est l'image résultante.
La première hélice fait 1/10 de tour lors de l'exposition:
Abonnez-vous aux chaînes:
@Ontol - les textes / vidéos les plus intéressants de tous les temps et des peuples, influençant l'image du monde
@META LEARNING - où je partage mes découvertes les plus utiles sur l'éducation et le rôle de l'informatique / des jeux dans l'éducation (ainsi que les réflexions d'Anton sur ce sujet Makarenko, Seymour Papert, Paul Graham, Joseph Licklider, Alan Kay)
L'image est légèrement déformée, mais rien de critique. L'hélice se déplacera désormais 10 fois plus vite, effectuant une rotation complète pendant l'exposition:
Cela ressemble déjà à l'image que nous avons vue au début. Cinq fois par exposition:
C'est déjà un peu trop, donc vous pouvez sortir des bobines. Amusons-nous et vérifions à quoi ressembleront différents objets à différentes vitesses de rotation par exposition.
Exactement la même hélice:
Grandes pales d'hélice:
Roue de voiture:
Nous pouvons percevoir l'effet de volet roulant comme une sorte de transformation des coordonnées d'un objet réel de «l'espace objet» à «l'espace image» d'un objet déformé. L'animation ci-dessous montre ce qui arrive au système de coordonnées cartésien lorsque le nombre de révolutions augmente. À basse vitesse, la déformation est insignifiante - le nombre augmente à un, et chaque côté du système de coordonnées se déplace séquentiellement vers le côté droit de l'image. C'est une transformation assez complexe à appréhender, mais facile à comprendre.
Soit l'image I (r, θ), l'objet réel (en rotation) sera f (r, θ), où (r, θ) sont des coordonnées polaires 2D. Nous avons choisi les coordonnées polaires pour cette tâche en raison du mouvement de rotation des objets.
L'objet tourne avec une fréquence angulaire ω et l'obturateur se déplace le long de l'image avec une vitesse v verticalement. À la position (r, θ) de l'image, la distance parcourue par l'obturateur depuis le début de l'exposition est y = rsinθ, où le temps écoulé depuis ce moment est (rsinθ) / v. Pendant ce temps, l'objet a tourné de (ω / v) rsinθ) radians. Ainsi, nous obtenons
I (r, θ) = f (r, θ + (ω / v) rsinθ),
qui est la transformation requise. Le rapport ω / v est proportionnel au nombre de rotations par exposition et paramètre la transformation.
Pour mieux comprendre les formes d'hélices évidentes, nous pouvons considérer un objet constitué d' hélices P , où f n'est différent de zéro que pour
θ = 2π / P, 4π / P… 2π = 2pπ / P pour 1 <p <P.
L'image I est non nulle pour θ + (ω / v) rsinθ = 2pπ / P ou
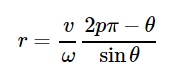
Dans le système de coordonnées cartésien, elle devient
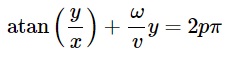
et nous aide à expliquer la raison pour laquelle les hélices prennent une forme en S - c'est simplement une fonction de l'arc tangente dans l'espace image. Cool. Ci-dessous, j'ai tracé cette fonction avec un ensemble de cinq pales d'hélice avec des décalages initiaux légèrement différents, vous pouvez le voir dans la lecture. Ils sont très similaires aux formes des animations ci-dessus.
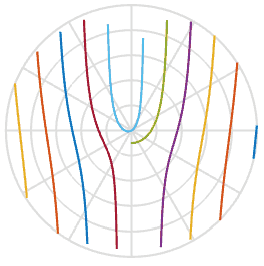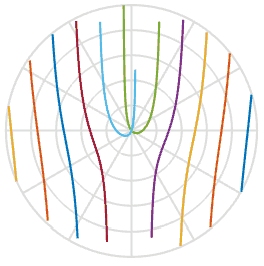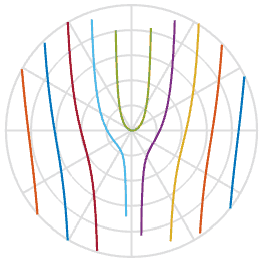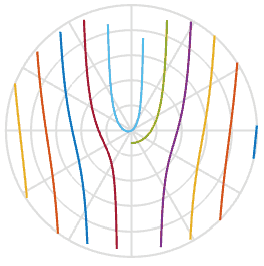
Puisque nous en avons appris un peu plus sur le processus, pouvons-nous réparer les photos endommagées? En utilisant l'une des images ci-dessus, je peux tracer une ligne à travers, faire pivoter et insérer ces pixels dans la nouvelle image. Dans l'animation ci-dessous, je scanne l'image de gauche, marquée d'une ligne rouge, puis je fais pivoter les pixels le long de cette ligne pour obtenir une nouvelle image. De cette façon, nous pouvons recréer l'image d'un objet réel, même si soudainement un volet roulant ennuyeux a gâché votre photo.
Eh, si j'étais meilleur avec Photoshop, j'extraireais les hélices de la photo originale sur Flickr, les éditerais et les remettrais dans la photo. Je pense que je sais ce que je ferai à l'avenir.
Si vous voulez connaître le nombre réel de lames sur la photo au début du post et la vitesse de rotation, vous pouvez lire cet excellent post Tumblr de Daniel Walsh , dans lequel il fournit une explication mathématique.
Il pense que nous pouvons compter le nombre de lames en soustrayant les lames «inférieures» de celles «supérieures», donc nous obtenons trois lames dans cette image. Nous savons également que l'hélice tourne environ deux fois pendant l'exposition, donc si nous essayons «d'annuler» la rotation à plusieurs vitesses différentes, nous obtenons quelque chose comme ceci:
Je devais déterminer où se trouvait le centre de l'hélice, alors j'ai dessiné un cercle. Apparemment, le centre devrait être quelque part à proximité. Malheureusement, une lame est manquante, mais il y a suffisamment d'informations pour l'afficher.
J'ai trouvé l'endroit où tout se croise le plus, donc à cette vitesse de rotation (2,39 tours par exposition), voici à quoi ressemblent l'image d'origine et les lames:
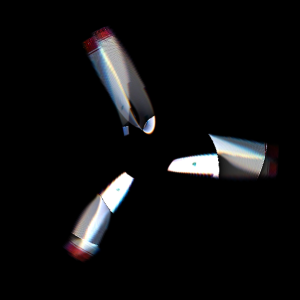
Malheureusement, l'image n'est pas parfaite, mais au moins elle est très proche de la réalité.
À propos de l'auteur: Jason Cole est un étudiant diplômé de Londres passionné de mathématiques, de physique et de visualisation de données. Voici son site Web . Et l'article a été publié ici .
Discussion sur les actualités des hackers
ajouter. vidéo
Abonnez-vous aux chaînes:
@Ontol - les textes / vidéos les plus intéressants de tous les temps et de tous les peuples, influençant l'image du monde
@META TRAINING , où je partage mes découvertes les plus utiles sur l'éducation et le rôle de l'informatique / des jeux dans l'éducation (ainsi que les réflexions d'Anton sur ce sujet Makarenko, Seymour Papert, Paul Graham, Joseph Licklider, Alan Kay)
Apprenez en détail comment obtenir un métier recherché à partir de zéro ou passer au niveau supérieur en compétences et en salaire en suivant les cours en ligne payés de SkillFactory:
- Cours d'apprentissage automatique (12 semaines)
- Apprendre la science des données à partir de zéro (12 mois)
- Profession analytique avec n'importe quel niveau de départ (9 mois)
- Cours Python pour le développement Web (9 mois)