L'apprentissage automatique (ML) change déjà le monde. Google utilise IO pour proposer et afficher des réponses aux recherches des utilisateurs. Netflix l'utilise pour recommander des films pour la soirée. Et Facebook l'utilise pour suggérer de nouveaux amis que vous connaissez peut-être.
L'apprentissage automatique n'a jamais été aussi important et, en même temps, si difficile à apprendre. Cette zone regorge de jargon et le nombre d'algorithmes de ML différents augmente chaque année.
Cet article vous présentera les concepts fondamentaux de l'apprentissage automatique. Plus précisément, nous discuterons des concepts de base des 9 algorithmes de ML les plus importants aujourd'hui.
Système de recommandation
Construire un système de recommandation complet à partir de 0 nécessite une connaissance approfondie de l'algèbre linéaire. Pour cette raison, si vous n'avez jamais étudié cette discipline, il vous sera peut-être difficile de comprendre certains des concepts de cette section.
Mais ne vous inquiétez pas, la bibliothèque Python scikit-learn facilite la création d'un CP. Vous n'avez donc pas besoin de cette connaissance approfondie de l'algèbre linéaire pour construire un CP fonctionnel.
Comment fonctionne le CP?
Il existe 2 principaux types de systèmes de recommandation:
- Basé sur le contenu
- Filtrage collaboratif
Un système basé sur le contenu fait des recommandations basées sur la similitude des éléments que vous avez déjà utilisés. Ces systèmes se comportent exactement comme vous vous attendez à ce que le CP se comporte.
Le filtrage collaboratif CP fournit des recommandations basées sur la connaissance de la manière dont l'utilisateur interagit avec les éléments (* remarque: les interactions avec les éléments d'autres utilisateurs dont le comportement est similaire à celui de l'utilisateur sont prises comme base). En d'autres termes, ils utilisent la «sagesse de la foule» (d'où le «collaboratif» au nom de la méthode).
Dans le monde réel, le filtrage CP collaboratif est bien plus courant qu'un système basé sur le contenu. Cela est principalement dû au fait qu'ils donnent généralement de meilleurs résultats. Certains experts trouvent également le système collaboratif plus facile à comprendre.
Le filtrage collaboratif CP a également une fonctionnalité unique qui ne se trouve pas dans un système basé sur le contenu. À savoir, ils ont la capacité d'apprendre les fonctionnalités par eux-mêmes.
Cela signifie qu'ils peuvent même commencer à définir la similitude des éléments en fonction de propriétés ou de traits que vous n'avez même pas fournis pour que ce système fonctionne.
Il existe 2 sous-catégories de filtrage collaboratif:
- Basé sur un modèle
- Basé sur le quartier
La bonne nouvelle est que vous n'avez pas besoin de connaître la différence entre ces deux types de filtrage CP collaboratif pour réussir dans le ML. Il suffit juste de savoir qu'il en existe plusieurs types.
Résumer
Voici un bref récapitulatif de ce que nous avons appris sur le système de recommandation dans cet article:
- Exemples de systèmes de recommandation dans le monde réel
- Différents types de système de recommandation et pourquoi le filtrage collaboratif est utilisé plus souvent que le système basé sur le contenu
- La relation entre le système de recommandation et l'algèbre linéaire
Régression linéaire
La régression linéaire est utilisée pour prédire une valeur y basée sur un ensemble de valeurs x.
Histoire de la régression linéaire
La régression linéaire (LR) a été inventée en 1800 par Francis Galton. Galton était un scientifique étudiant le lien entre parents et enfants. Plus précisément, Galton a étudié la relation entre la croissance des pères et la croissance de leurs fils. La première découverte de Galton était le fait que la croissance des fils, en règle générale, était à peu près la même que celle de leurs pères. Ce qui n’est pas surprenant.
Plus tard, Galton a découvert quelque chose de plus intéressant. La croissance du fils, en règle générale, était plus proche de la taille globale moyenne de toutes les personnes que de la croissance de son propre père.
Galton a appelé ce phénomène régression . Plus précisément, il a déclaré: "La taille du fils a tendance à régresser (ou à se déplacer vers) la taille moyenne."
Cela a conduit à tout un champ de statistiques et d'apprentissage automatique appelé régression.
Mathématiques de régression linéaire
Dans le processus de création d'un modèle de régression, tout ce que nous essayons de faire est de tracer une ligne aussi près que possible de chaque point de l'ensemble de données.
Un exemple typique de cette approche est la méthode de régression linéaire des «moindres carrés», qui calcule la proximité d'une ligne dans le sens de haut en bas.
Exemple d'illustration:
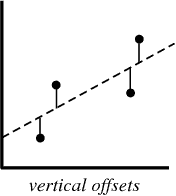
lorsque vous créez un modèle de régression, votre produit final est une équation que vous pouvez utiliser pour prédire les valeurs y pour la valeur x sans connaître la valeur y à l'avance.
Régression logistique
La régression logistique est similaire à la régression linéaire, sauf qu'au lieu de calculer la valeur de y, elle évalue à quelle catégorie appartient un point de données donné.
Qu'est-ce que la régression logistique?
La régression logistique est un modèle d'apprentissage automatique utilisé pour résoudre des problèmes de classification.
Voici quelques exemples des tâches de classification du MO:
- Email spam (spam ou pas spam?)
- Réclamation d'assurance automobile (indemnisation ou réparation?)
- Diagnostic des maladies
Chacune de ces tâches comporte clairement 2 catégories, ce qui en fait des exemples de tâches de classification binaire.
La régression logistique fonctionne bien pour les problèmes de classification binaire - nous attribuons simplement différentes catégories à 0 et 1, respectivement.
Pourquoi la régression logistique? Parce que vous ne pouvez pas utiliser de régression linéaire pour les prédictions de classification binaire. Cela ne fonctionnera tout simplement pas car vous essaierez de tracer une ligne droite à travers un ensemble de données avec deux valeurs possibles.
Cette image peut vous aider à comprendre pourquoi la régression linéaire est mauvaise pour la classification binaire:
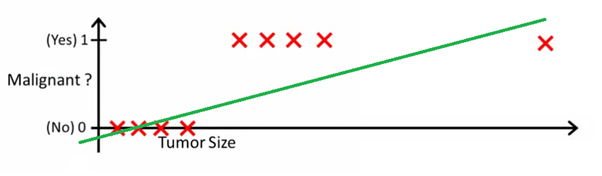
Dans cette image, l'axe des y représente la probabilité que la tumeur soit maligne. Les valeurs 1-y représentent la probabilité que la tumeur soit bénigne. Comme vous pouvez le constater, le modèle de régression linéaire fonctionne très mal pour prédire la probabilité de la plupart des observations de l'ensemble de données.
C'est pourquoi le modèle de régression logistique est utile. Il a une inclinaison vers la ligne de meilleur ajustement, ce qui le rend beaucoup plus approprié pour prédire des données qualitatives (catégoriques).
Voici un exemple qui compare des modèles de régression linéaire et logistique sur les mêmes données:
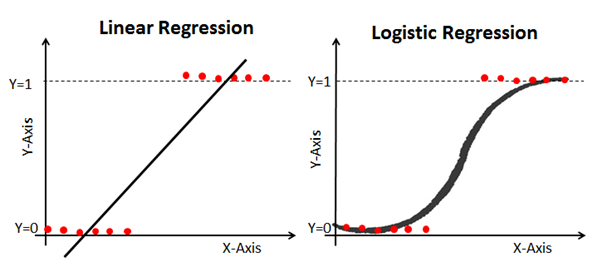
Sigmoïde (la fonction sigmoïde)
La raison pour laquelle la régression logistique est déformée est qu'elle n'utilise pas d'équation linéaire pour la calculer. Au lieu de cela, le modèle de régression logistique est construit à l'aide d'un sigmoïde (également appelé fonction logistique car il est utilisé dans la régression logistique).
Vous n'avez pas à mémoriser le sigmoïde à fond pour réussir en ML. Néanmoins, il sera utile d'avoir une idée de cette fonctionnalité.
Formule sigmoïde: La
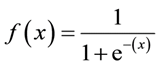
principale caractéristique d'un sigmoïde, qui vaut la peine d'être traitée - quelle que soit la valeur que vous passez à cette fonction, elle retournera toujours une valeur comprise entre 0-1.
Utilisation d'un modèle de régression logistique pour les prédictions
Afin d'utiliser la régression logistique pour les prédictions, vous devez généralement définir avec précision le point de coupure. Ce point de coupure est généralement de 0,5.
Utilisons notre exemple de diagnostic de cancer du graphique précédent pour voir ce principe en pratique. Si le modèle de régression logistique renvoie une valeur inférieure à 0,5, ce point de données sera classé comme bénin. De même, si le sigmoïde donne une valeur supérieure à 0,5, la tumeur est classée comme maligne.
Utilisation d'une matrice d'erreur pour mesurer l'efficacité de la régression logistique
La matrice d'erreur peut être utilisée comme un outil pour comparer les scores vrai positif, vrai négatif, faux positif et faux négatif en MO.
La matrice d'erreur est particulièrement utile lorsqu'elle est utilisée pour mesurer les performances d'un modèle de régression logistique. Voici un exemple de la façon dont nous pouvons utiliser la matrice d'erreur:
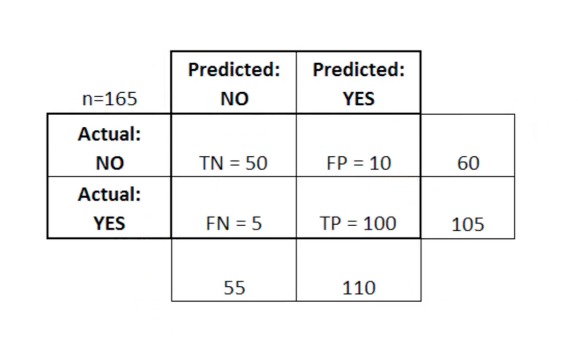
Dans ce tableau, TN signifie vrai négatif, FN signifie faux négatif, FP signifie faux positif, TP signifie vrai positif.
Une matrice d'erreur est utile pour évaluer un modèle s'il y a des quadrants «faibles» dans la matrice d'erreur. Par exemple, elle peut avoir un nombre anormalement élevé de faux positifs.
Il est également très utile dans certains cas de s'assurer que votre modèle fonctionne correctement dans une zone particulièrement dangereuse de la matrice d'erreur.
Dans cet exemple de diagnostic de cancer, par exemple, vous souhaitez vous assurer que votre modèle n'a pas trop de faux positifs car cela signifie que vous avez diagnostiqué la tumeur maligne de quelqu'un comme bénigne.
Résumer
Dans cette section, vous avez fait votre première connaissance du modèle ML - régression logistique.
Voici un bref résumé de ce que vous avez appris sur la régression logistique:
- Types de problèmes de classification pouvant être résolus par régression logistique
- La fonction logistique (sigmoïde) donne toujours une valeur entre 0 et 1
- Comment utiliser les seuils pour prédire avec un modèle de régression logistique
- Pourquoi une matrice d'erreur est-elle utile pour mesurer les performances d'un modèle de régression logistique
Algorithme K-Nearest Neighbours
L'algorithme des k plus proches voisins peut aider à résoudre le problème de classification dans le cas où il y a plus de 2 catégories.
Quel est l'algorithme des k-plus proches voisins?
Il s'agit d'un algorithme de classification basé sur un principe simple. En fait, le principe est si simple qu'il vaut mieux le démontrer par un exemple.
Imaginez que vous ayez des données de taille et de poids pour les footballeurs et les basketteurs. L'algorithme des k-plus proches voisins peut être utilisé pour prédire si un nouveau joueur est un joueur de football ou un joueur de basket-ball. Pour ce faire, l'algorithme détermine les K points de données les plus proches de l'objet d'étude.
Cette image démontre ce principe avec le paramètre K = 3:
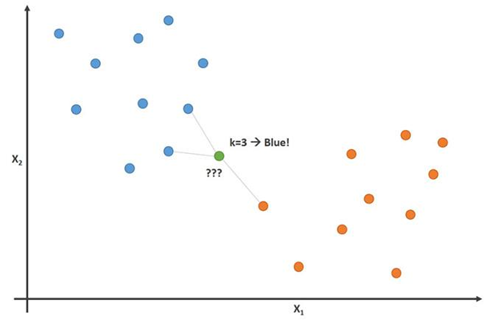
Sur cette image, les joueurs de football sont bleus et les basketteurs sont orange. Le point que nous essayons de classer est de couleur verte. Étant donné que la plupart des marques (2 sur 3) les plus proches du point vert sont de couleur bleue (joueurs de football), alors l'algorithme des K-plus proches voisins prédit que le nouveau joueur sera également un joueur de football.
Comment construire un algorithme K-plus proche voisins
Les principales étapes de construction de cet algorithme:
- Collectez toutes les données
- Calculer la distance euclidienne entre le nouveau point de données x et tous les autres points de l'ensemble de données
- Trier les points du jeu de données par ordre croissant de distance à x
- Prédire la réponse en utilisant la même catégorie que la plupart des données K les plus proches de x
Importance de la variable K dans l'algorithme des K voisins les plus proches
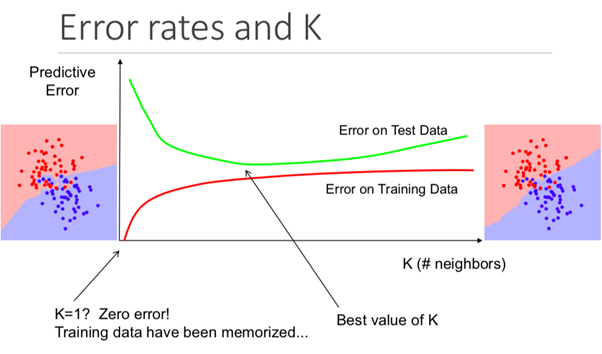
Bien que cela ne soit pas évident dès le départ, la modification de la valeur K dans cet algorithme changera la catégorie dans laquelle le nouveau point de données appartient.
Plus précisément, une valeur K trop faible entraînera votre modèle à prédire avec précision sur l'ensemble de données d'entraînement, mais sera extrêmement inefficace sur les données de test. De plus, avoir un K trop élevé rendra le modèle inutilement complexe.
L'illustration ci-dessous montre parfaitement cet effet:
Avantages et inconvénients de l'algorithme des K-plus proches voisins
Pour résumer notre introduction à cet algorithme, discutons brièvement des avantages et des inconvénients de son utilisation.
Avantages:
- L'algorithme est simple et facile à comprendre
- Formation de modèle trivial sur de nouvelles données d'entraînement
- Fonctionne avec n'importe quel nombre de catégories dans une tâche de classification
- Ajoutez facilement plus de données à de nombreuses données
- Le modèle ne prend que 2 paramètres: K et la métrique de distance que vous souhaitez utiliser (généralement la distance euclidienne)
Moins:
- Coût de calcul élevé, car vous devez traiter toute la quantité de données
- Ne fonctionne pas aussi bien avec les paramètres catégoriels
Résumer
Un résumé de ce que vous venez d'apprendre sur l'algorithme K-Nearest Neighbor:
- Un exemple de problème de classification (joueurs de football ou de basketball) que l'algorithme peut résoudre
- Comment l'algorithme utilise la distance euclidienne aux points voisins pour prédire à quelle catégorie appartient un nouveau point de données
- Pourquoi les valeurs K sont importantes pour la prévision
- Avantages et inconvénients de l'utilisation de l'algorithme des K-plus proches voisins
Arbres de décision et forêts aléatoires
L'arbre de décision et la forêt aléatoire sont 2 exemples de méthode d'arbre. Plus précisément, les arbres de décision sont des modèles ML utilisés pour prédire en bouclant chaque fonction d'un ensemble de données une par une. Une forêt aléatoire est un ensemble (comité) d'arbres de décision qui utilisent des ordres aléatoires d'objets dans un ensemble de données.
Qu'est-ce qu'une méthode arborescente?
Avant de plonger dans les fondements théoriques de la méthode arborescente en ML, il est utile de commencer par un exemple.
Imaginez que vous jouez au basket tous les lundis. De plus, vous invitez toujours le même ami à venir jouer avec vous. Parfois, un ami vient, parfois non. La décision de venir ou non dépend de nombreux facteurs: quel type de temps, de température, de vent et de fatigue. Vous commencez à remarquer ces fonctionnalités et à les suivre avec la décision de votre ami de jouer ou non.
Vous pouvez utiliser ces données pour prédire si votre ami vient aujourd'hui ou non. Une technique que vous pouvez utiliser est un arbre de décision. Voici à quoi cela ressemble:
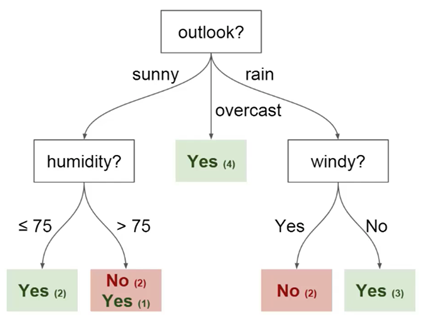
Chaque arbre de décision comporte 2 types d'éléments:
- Nœuds: endroits où l'arbre est divisé en fonction de la valeur d'un certain paramètre
- Bords: le résultat de la scission menant au nœud suivant
Vous pouvez voir que le diagramme a des nœuds pour les perspectives, l'humidité et le
vent. Et aussi les facettes pour chaque valeur potentielle de chacun de ces paramètres.
Voici quelques définitions supplémentaires que vous devez comprendre avant de commencer:
- Racine - le nœud à partir duquel commence la division de l'arbre
- Feuilles - les nœuds finaux qui prédisent le résultat final
Vous avez maintenant une compréhension de base de ce qu'est un arbre de décision. Nous verrons comment créer un tel arbre à partir de zéro dans la section suivante.
Comment créer un arbre de décision à partir de zéro
Construire un arbre de décision est plus délicat qu'il n'y paraît. En effet, décider dans quelles ramifications (caractéristiques) diviser vos données (qui est un sujet lié à l'entropie et à l'acquisition de données) est une tâche mathématiquement difficile.
Pour résoudre ce problème, les spécialistes du ML utilisent généralement de nombreux arbres de décision, appliquant des ensembles aléatoires de caractéristiques choisis pour diviser l'arbre en eux. En d'autres termes, de nouveaux ensembles aléatoires de caractéristiques sont choisis pour chaque arbre séparé, à chaque partition distincte. Cette technique est appelée forêts aléatoires.
En général, les experts choisissent généralement la taille d'un ensemble aléatoire d'entités (notée m) de telle sorte que ce soit la racine carrée du nombre total d'entités dans l'ensemble de données (notée p). En bref, m est la racine carrée de p, puis une caractéristique spécifique est choisie au hasard parmi m.
Avantages de l'utilisation d'une forêt aléatoire
Imaginez que vous travaillez avec un grand nombre de données qui ont une caractéristique «forte». En d'autres termes, il y a une caractéristique de cet ensemble de données qui est beaucoup plus prévisible en termes de résultat final que d'autres caractéristiques de cet ensemble de données.
Si vous créez un arbre de décision à la main, il est logique d'utiliser cette caractéristique pour la partition «supérieure» de votre arbre. Cela signifie que vous aurez plusieurs arbres dont les prédictions sont fortement corrélées.
Nous voulons éviter cela car l'utilisation de la moyenne de variables hautement corrélées ne réduit pas significativement la variance. En utilisant des ensembles aléatoires de caractéristiques pour chaque arbre dans une forêt aléatoire, nous décorrélons les arbres et la variance du modèle résultant est réduite. Cette décorrélation est un avantage majeur dans l'utilisation de forêts aléatoires par rapport aux arbres de décision construits à la main.
Résumer
Voici donc un bref résumé de ce que vous venez d'apprendre sur les arbres de décision et les forêts aléatoires:
- Un exemple de problème dont la solution peut être prédite à l'aide d'un arbre de décision
- Éléments de l'arbre de décision: nœuds, faces, racines et feuilles
- Comment l'utilisation d'un ensemble aléatoire de caractéristiques nous permet de construire une forêt aléatoire
- Pourquoi l'utilisation d'une forêt aléatoire pour la décorrélation des variables peut être utile pour réduire la variance du modèle résultant
Machines vectorielles de soutien
Les machines vectorielles de support sont un algorithme de classification (bien que, techniquement parlant, elles puissent également être utilisées pour résoudre des problèmes de régression) qui divise un ensemble de données en catégories au niveau des plus grands «écarts» entre les catégories. Ce concept devient plus clair lorsque vous regardez l'exemple suivant.
Qu'est-ce que la machine vectorielle de support?
Une machine à vecteurs de support (SVM) est un modèle ML supervisé avec des algorithmes d'apprentissage appropriés qui analysent les données et reconnaissent les modèles. Le SVM peut être utilisé à la fois pour les tâches de classification et l'analyse de régression. Dans cet article, nous examinerons spécifiquement l'utilisation de machines vectorielles de support pour résoudre les problèmes de classification.
Comment fonctionne le protocole d'entente?
Voyons de plus près comment fonctionne réellement le protocole d'entente.
On nous donne un ensemble d'exemples d'entraînement, chacun d'eux étant marqué comme appartenant à l'une des 2 catégories, et en utilisant cet ensemble de SVM, nous construisons un modèle. Ce modèle classe les nouveaux exemples dans l'une des deux catégories. Cela fait du SVM un classificateur linéaire binaire improbable.
Le protocole d'entente utilise la géométrie pour faire des prédictions par catégorie. Plus spécifiquement, la machine à vecteurs de support mappe les points de données sous forme de points dans l'espace et les catégorise de manière à ce qu'ils soient séparés par un espace aussi large que possible. La prédiction selon laquelle les nouveaux points de données appartiendront à une catégorie particulière est basée sur le côté du point de rupture.
Voici un exemple de visualisation pour vous aider à comprendre l'intuition du MOU:
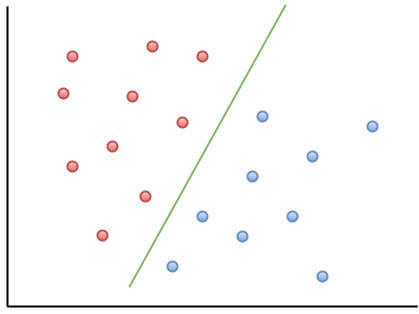
Comme vous pouvez le constater, si un nouveau point de données tombe à gauche de la ligne verte, il sera appelé «rouge», et s'il se trouve à droite, il sera appelé «bleu». Cette ligne verte s'appelle un hyperplan et est un terme important pour travailler avec les PE.
Jetons un œil à la représentation visuelle suivante du SVM:
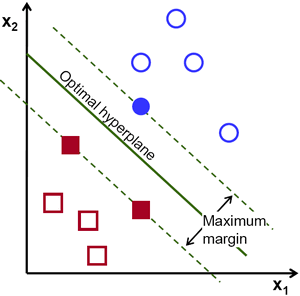
Dans ce diagramme, l'hyperplan est étiqueté comme «l'hyperplan optimal». La théorie de la machine vectorielle de support définit un hyperplan optimal comme un hyperplan qui maximise le champ entre les deux points de données les plus proches de différentes catégories.
Comme vous pouvez le voir, la limite du champ affecte en effet 3 points de données - 2 de la catégorie rouge et 1 du bleu. Ces points, qui sont en contact avec la bordure du champ, sont appelés vecteurs de support - d'où leur nom.
Résumer
Voici un aperçu rapide de ce que vous venez d'apprendre sur les machines vectorielles de support:
- Le protocole d'accord est un exemple d'algorithme de ML supervisé
- Le vecteur de support peut être utilisé pour résoudre les problèmes de classification et pour l'analyse de régression.
- Comment le protocole d'entente catégorise les données à l'aide d'un hyperplan qui maximise la marge entre les catégories dans l'ensemble de données
- Les points de données qui touchent les limites du champ de division sont appelés vecteurs de support. C'est de là que vient le nom de la méthode.
Clustering K-Means
La méthode K-Means est un algorithme d'apprentissage automatique non supervisé. Cela signifie qu'il accepte des données non étiquetées et tente de regrouper des grappes d'observations similaires dans vos données. La méthode K-Means est extrêmement utile pour résoudre des applications du monde réel. Voici des exemples de plusieurs tâches qui correspondent à ce modèle:
- Segmentation des clients pour les équipes marketing
- Classification des documents
- Optimiser les itinéraires d'expédition pour des entreprises comme Amazon, UPS ou FedEx
- Identifier et répondre aux lieux criminels de la ville
- Analyse sportive professionnelle
- Prédire et prévenir la cybercriminalité
Le principal objectif de la méthode K-Means est de diviser l'ensemble de données en groupes distincts afin que les éléments de chaque groupe soient similaires les uns aux autres.
Voici une représentation visuelle de ce à quoi cela ressemble en pratique:
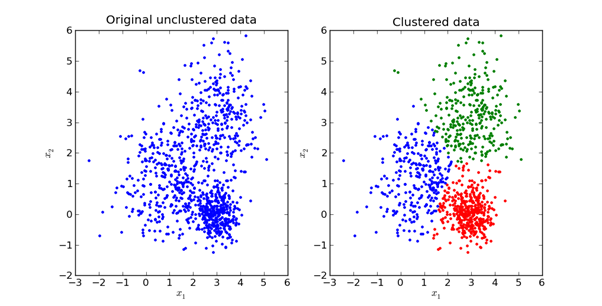
Nous explorerons les mathématiques derrière la méthode K-Means dans la prochaine section de cet article.
Comment fonctionne la méthode K-Means?
La première étape de l'utilisation de la méthode K-Means consiste à choisir le nombre de groupes dans lesquels vous souhaitez diviser vos données. Cette quantité est la valeur de K, reflétée dans le nom de l'algorithme. Le choix de la valeur K dans la méthode K-Means est très important. Nous verrons un peu plus tard comment choisir la valeur K correcte.
Ensuite, vous devez sélectionner au hasard un point dans l'ensemble de données et l'assigner à un cluster aléatoire. Cela vous donnera la position de départ des données à laquelle vous exécutez la prochaine itération jusqu'à ce que les clusters cessent de changer:
- Calcul du centroïde (centre de gravité) de chaque cluster en prenant le vecteur moyen des points de cet cluster
- Réaffecter chaque point de données au cluster dont le centre de gravité est le plus proche du point
Choix d'une valeur K appropriée dans la méthode des K-Means
À proprement parler, il est assez difficile de choisir une valeur K appropriée. Il n'y a pas de «bonne» réponse pour choisir la «meilleure» valeur K. Une méthode souvent utilisée par les professionnels du ML est la «méthode du coude».
Pour utiliser cette méthode, la première chose à faire est de calculer la somme des erreurs quadratiques - l'écart type de votre algorithme pour un groupe de valeurs K. L'écart type de la méthode K-means est défini comme la somme des carrés des distances entre chaque point de données du cluster. et le centre de gravité de cet amas.
À titre d'exemple de cette étape, vous pouvez calculer l'écart type pour les valeurs K de 2, 4, 6, 8 et 10. Ensuite, vous voudrez générer un graphique de l'écart type et de ces valeurs K. Vous verrez que l'écart diminue à mesure que la valeur K augmente.
Et cela a du sens: plus vous créez de catégories à partir d'un ensemble de données, plus chaque point de données est susceptible d'être proche du centre du cluster de ce point.
Cela dit, l'idée principale de la méthode du coude est de choisir la valeur K à laquelle le RMS ralentira considérablement le taux de déclin. Cette forte baisse forme un «coude» sur le graphique.
À titre d'exemple, voici un graphique de RMS en fonction de K. Dans ce cas, la méthode du coude suggérera d'utiliser une valeur K d'environ 6.
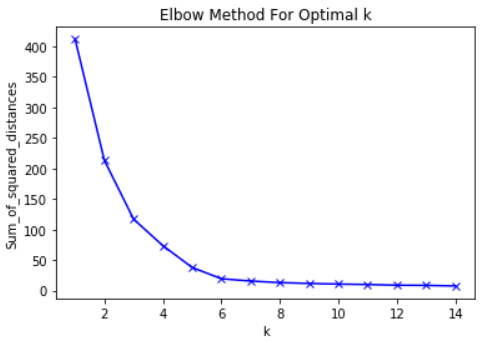
Il est important que K = 6 soit simplement une estimation d'une valeur K acceptable. Il n'y a pas de «meilleure» valeur K dans la méthode K-Means. Comme beaucoup de choses dans le ML, c'est une décision très situationnelle.
Résumer
Voici un bref aperçu de ce que vous venez d'apprendre dans cette section:
- Exemples de tâches ML sans enseignant qui peuvent être résolues par la méthode K-means
- Principes de base de la méthode K-means
- Comment fonctionne K-Means
- Comment utiliser la méthode du coude pour sélectionner la valeur appropriée pour le paramètre K dans cet algorithme
Analyse des composants principaux
L'analyse des composants principaux est utilisée pour transformer un ensemble de données avec de nombreux paramètres en un nouvel ensemble de données avec moins de paramètres, et chaque nouveau paramètre de cet ensemble de données est une combinaison linéaire de paramètres déjà existants. Ces données transformées ont tendance à justifier une grande partie de la variance de l'ensemble de données d'origine avec beaucoup plus de simplicité.
Qu'est-ce que la méthode des composants principaux?
L'analyse en composantes principales (ACP) est une technique d'apprentissage automatique utilisée pour étudier les relations entre des ensembles de variables. En d'autres termes, l'ACP examine des ensembles de variables afin de déterminer la structure de base de ces variables. L'ACP est aussi parfois appelée analyse factorielle.
Sur la base de cette description, vous pourriez penser que l'ACP est très similaire à la régression linéaire. Mais ce n'est pas le cas. En fait, ces 2 techniques présentent plusieurs différences importantes.
Différences entre la régression linéaire et l'ACP
La régression linéaire détermine la ligne de meilleur ajustement dans l'ensemble de données. L'analyse en composantes principales identifie plusieurs lignes orthogonales de meilleur ajustement pour un jeu de données.
Si vous n'êtes pas familier avec le terme orthogonal, cela signifie simplement que les lignes sont perpendiculaires les unes aux autres, comme le nord, l'est, le sud et l'ouest sur une carte.
Regardons un exemple pour vous aider à mieux comprendre cela.

Jetez un œil aux étiquettes des axes dans cette image. La composante principale de l'axe des x explique 73% de la variance de cet ensemble de données. La composante principale de l'axe des y explique environ 23% de la variance de l'ensemble de données.
Cela signifie que 4% de la variance reste inexpliquée. Vous pouvez réduire ce nombre en ajoutant plus de composants principaux à votre analyse.
Résumer
Un résumé de ce que vous venez d'apprendre sur l'analyse en composantes principales:
- PCA essaie de trouver des facteurs orthogonaux qui déterminent la variabilité dans un jeu de données
- Différence entre la régression linéaire et l'ACP
- À quoi ressemblent les composants principaux orthogonaux lorsqu'ils sont rendus dans un jeu de données
- L'ajout de composants principaux supplémentaires peut aider à expliquer la variance plus précisément dans l'ensemble de données