👩🏾‍🤝‍👩🏼 ✋🏼 🙎🏽 Construction de la courbe d'actualisation. Programme éducatif pour un geek, partie 5 🈯️ 👩🏼‍🤝‍👨🏻 🉐

Apprenons à construire une courbe de remise. Je dirai tout de suite: il est très important de disposer de données de marché pertinentes. Si vous recherchez des swaps de taux d'intérêt pour le dollar, l'euro ou une autre devise, il n'y a pas beaucoup d'informations ouvertes sur Internet. La plupart des données sont disponibles soit via des terminaux de négociation, soit auprès de sociétés spéciales - des fournisseurs de données de marché. J'ai trouvé des données sur les couronnes danoise, suédoise et norvégienne, ainsi que des données sur l'euro et le dollar sur le site Web d'un grand groupe bancaire scandinave.

Ensuite, nous essayerons de construire une courbe de remise pour la couronne suédoise.

Cet article est une version adaptée de ma troisième conférence vidéo " Construire la courbe de remise " dans le cadre du cours Finmath for Fintech.

Ainsi, notre courbe de remise pour la couronne correspondra aux taux au jour le jour. La première chose que nous connaissons est le soi-disant taux de base - le taux des dépôts à découvert (prêts). En outre, il existe des swaps connus allant d'un an à trente ans. Pour illustrer la méthode, nous allons tracer une courbe jusqu'à dix ans. Les valeurs actuelles des données de marché peuvent être vues dans cette image:

Pour commencer à tracer la courbe, nous devons faire quelques hypothèses.

Supposons par souci de simplicité que nos swaps sont des swaps flottants fixes avec une périodicité de paiements tous les six mois. Voici le diagramme d'un swap d'un an. Nous savons qu'au début, le taux de base est de zéro pour cent. Pour calculer le juste prix du swap, nous devons connaître la valeur du facteur d'actualisation de six mois et du facteur d'actualisation de 12 mois. Qu'aurons-nous comme "jambe" flottante? Supposons que nous paierons la valeur moyenne au jour le jour pour chacune des plages. Autrement dit, la valeur de la «jambe» flottante jusqu'à six mois - ce sera la valeur moyenne au jour le jour sur 180 jours. L'étape flottante pour le point 12 mois sera la même, mais ici il y aura une sommation du jour 181 au jour 360.

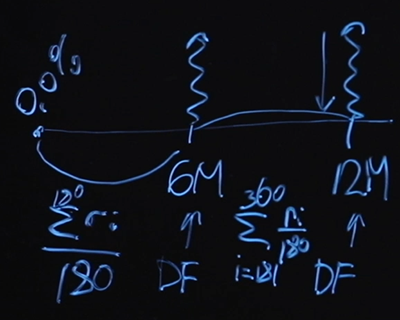
Cette méthode de calcul de la moyenne est largement connue. C'est ce qu'on appelle le swap d'indice du jour au lendemain et est très souvent utilisé dans les produits du marché. La jambe flottante est ici définie comme la moyenne sur la période.

Nous connaissons le taux de base et le coût du swap. Évidemment, si nous écrivons la formule du juste prix «de front», alors nous aurons trop d'inconnues. Nous ne connaissons pas le facteur d'actualisation pour 6 mois, le facteur d'actualisation pour 12 mois, et nous ne connaissons pas les valeurs des taux d'intérêt sauf pour un - le tout premier. Trop d'inconnues et une seule équation.

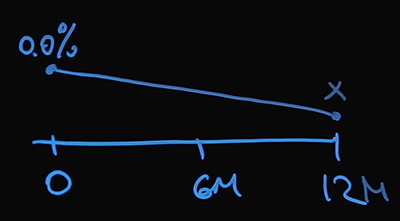
L'hypothèse suivante nous aidera à résoudre ce problème. Nous connaissons le taux d'intérêt au point zéro - c'est le taux de base. Nous supposerons que nos taux d'intérêt évoluent de manière linéaire. Désignons par X la valeur du taux d'intérêt au point de 12 mois.

À 6 mois, ce sera X / 2 (la moyenne arithmétique entre zéro et X), et nous pouvons trouver la valeur du taux d'intérêt à n'importe quel jour arbitraire. Et il n'y a rien de difficile à calculer notre taux d'intérêt variable aux points 6 et 12 mois:

\begin{array}{rcl} L_{1} & = & \frac{X}{4} \end{array}

$\begin{eqnarray} L_1&=& \frac{X}{4} \end{eqnarray}$

\begin{array}{rcl} L_{1} & = & \frac{3 X}{4} \end{array}

$\begin{eqnarray} L_1&=& \frac{3X}{4} \end{eqnarray}$

Passons maintenant aux facteurs de remise. Nous utilisons une courbe d'actualisation basée sur le taux au jour le jour. Par conséquent, le facteur d'actualisation au point six mois est le produit de 180 facteurs d'actualisation à chaque point, et ce sera évidemment une sorte de fonction de X. Le

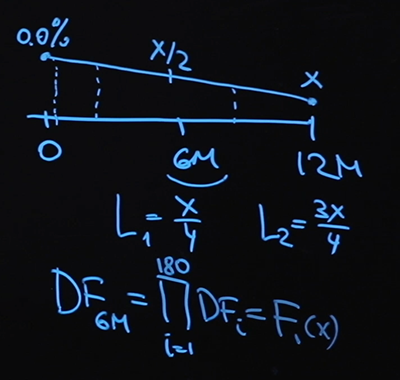
facteur d'actualisation au point 12 mois est construit de la même manière avec la seule différence dont j'ai besoin plus de multiplicateurs. Ce sera également une fonction de X.

Ainsi, les facteurs d'actualisation sont exprimés en termes de X, il y a aussi les première et deuxième valeurs du taux variable. Passons à l'écriture de l'équation. Nous connaissons la valeur du prix du swap, disons qu'il est égal à P. Rappelez-vous l'équation du juste prix. Nous devons multiplier P par le facteur d'actualisation au point de douze mois et égaler la somme suivante:

Permettez-moi de vous rappeler que le facteur d'actualisation pour un jour sera déterminé par la formule suivante:

\begin{array}{rcl} D F_{i} & = & \frac{1}{(1 + \frac{r_{i}}{360})} \end{array}

$\begin{eqnarray} DF_i&=& \frac{1}{(1+\frac{r_i}{360})} \end{eqnarray}$

où r _i est la valeur du taux d'intérêt. J'utilise le nombre 360 en supposant qu'il y a 360 jours dans une année (c'est une convention très courante pour les calendriers). A tout moment, on sait exprimer le facteur d'actualisation, r _i exprimé en termes de X, par interpolation linéaire. Notre équation se révèle être avec une seule inconnue, et elle peut être résolue à l'aide de méthodes numériques. Comment faire - voir le code Python .

Ainsi, nous savons comment trouver la valeur de notre taux au point 1 an. En utilisant l'hypothèse d'interpolation linéaire et basée sur la valeur de swap que nous connaissons du marché, nous trouverons notre valeur pour X. Ici, nous avons tracé la première section de notre courbe:

Maintenant, pour calculer le prix du swap pour deux ans, nous avons besoin de la valeur au point 6 mois, 12 mois, 18 mois et 2 ans. Nous utiliserons exactement la même hypothèse que la dernière fois. Appelons la valeur du taux souhaité Y et utilisons également l'hypothèse sur la ligne d'interpolation, en restaurant la deuxième section de la courbe. Ainsi, étape par étape, nous atteindrons la fin - jusqu'à 10 ans.

Cette méthode est appelée bootstrap . Ce n'est pas parfait ou le seul correct, mais il est assez simple à implémenter et à comprendre - la méthode bootstrap est excellente comme niveau de départ.

Nous avons trouvé la courbe de remise. Qu'est-ce que ça nous donne? Formellement parlant, ce sont les valeurs du taux du financement à un jour à tout moment dans le futur jusqu'à dix ans. Vous demandez probablement: "Qui en a besoin?" En effet, il est difficile d'imaginer un scénario où un client vient vers vous et vous dit: «Je veux ouvrir un dépôt d'un jour, qui débutera dans 567 jours». C'est une situation plutôt incompréhensible, et il ne faut pas percevoir la courbe construite sous une forme aussi directe.

Imaginons que nous ayons une sorte de paiement dans le futur, disons sept ans et demi. Question: comment connaissons-nous sa valeur actuelle?

C'est exactement la question à laquelle la courbe d'actualisation répondra. Nous allons parcourir chaque point de la courbe, calculer le facteur de réduction à chaque point et terminer notre voyage au point pendant sept ans et demi, trouver le facteur de réduction résultant, multiplier par le paiement - ce sera un prix honnête.

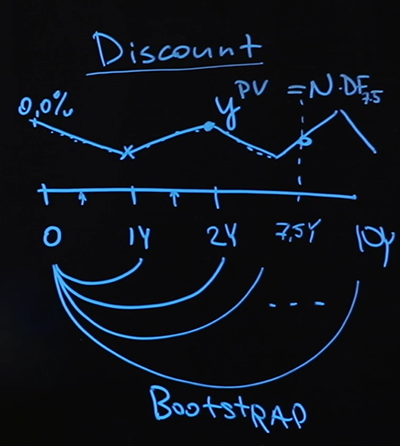
Le modèle que j'ai utilisé, à savoir quels taux flottants j'ai pris, comment j'ai interpolé les valeurs intermédiaires, et en général le fait que j'ai choisi l'interpolation était très déterminé par le type de données dont je disposais. J'avais très peu de données - juste un taux de base et des valeurs de swap. Si plus de données sont disponibles pour moi, ou si elles sont différentes, je changerai probablement de modèle. Mais la méthode bootstrap (lorsque vous tracez la courbe d'abord sur une courte section, puis tracez de plus en plus loin, en vous basant sur les valeurs obtenues précédemment) s'applique toujours.

Maintenant, rappelez-vous qu'en plus des courbes de remise, nous avons besoin de courbes LIBOR (TIBOR, EURIBOR, etc.). La différence réside dans les outils que nous ajoutons à notre modèle de calcul. Nous chercherons les contrats contenant du LIBOR et de la même manière, en utilisant la méthode bootstrap, nous reconstruirons la courbe LIBOR.

Si vous devez construire une vraie courbe LIBOR, faites très attention aux outils que vous utilisez pour la construire, évaluez soigneusement le modèle que vous utiliserez. Dans ce cas, j'ai utilisé l'actualisation du jour au lendemain, mais une méthode différente est nécessaire pour construire la courbe LIBOR. Très probablement, la remise sera tous les trois ou six mois, selon l'instrument. Si vous disposez de suffisamment de données, vous pouvez tracer une courbe LIBOR, une courbe EURIBOR, une courbe TIBOR et toute autre.

Si un client vient à vous avec les mots: «Je veux un swap de taux d'intérêt non pas pour dix ans, mais pour 134 mois, au cours desquels je paierai le LIBOR flottant tous les 25 jours», ce n'est pas un problème. Nous avons une courbe LIBOR, nous utilisons l'hypothèse d'interpolation, nous pouvons restaurer la valeur LIBOR à tout moment. Nous connaissons la valeur de la courbe d'actualisation à chaque point, nous pouvons également calculer tous les paiements et trouver le prix même de la «jambe» fixe qui équilibre ces paiements flottants. Ainsi, vous pouvez trouver les valeurs de prix justes pour absolument n'importe quel instrument en traçant plusieurs courbes.

Alors revenons sur les faits saillants. J'ai pris les données disponibles et formulé quelques hypothèses. Tout d'abord, le calendrier des paiements: à quelle fréquence, à quelle fréquence chaque partie paie une jambe fixe et une jambe flottante. Deuxièmement, comment vais-je calculer la mise sur la jambe flottante? La troisième hypothèse concerne l'interpolation linéaire des paris. En utilisant ces trois hypothèses, j'ai formulé plusieurs équations non linéaires, que j'ai résolues numériquement. Le cahier Jupyter peut être trouvé ici. Séquentiellement, en partant du segment le plus court d'un an, puis de deux ans, trois, etc., j'ai reconstruit la courbe sur un intervalle allant jusqu'à 10 ans. C'est ma courbe de remise que je peux utiliser pour évaluer n'importe quel instrument. Cette méthode s'appelle bootstrap: le segment de la courbe, que j'ai compté au tout début, j'utilise dans la deuxième étape, sinon,ce que j'ai obtenu dans la deuxième étape, je l'utilise pour la troisième étape et ainsi de suite, jusqu'à ce que la courbe soit complètement formée.

J'espère que maintenant vous ne «flottez» plus dans le sujet des taux d'intérêt flottants et parmi les taux d'intérêt des swaps, vous pouvez trouver de la vanille. Et vous pouvez également créer n'importe quelle courbe en utilisant la méthode bootstrap.

Tous les articles de cette série

Construction de la courbe d'actualisation. Programme éducatif pour un geek, partie 5

More articles: