
Dans le processus de développement d'un jeu dans des catégories de genre complètement différentes, il peut être nécessaire de «lancer» un objet de jeu le long d'une courbe douce à une vitesse constante ou contrôlée, que ce soit un camion se déplaçant de la ville A à la ville B, un missile tiré le long d'une trajectoire rusée ou un avion ennemi effectuer une manœuvre fixe.
Probablement, tous ceux qui sont liés au sujet connaissent ou du moins ont entendu parler des courbes de Bézier, des B-splines, des splines Hermite et d'autres splines d'interpolation et de lissage et suggéreraient absolument d'utiliser l'une d'entre elles dans la situation décrite, mais tout n'est pas si simple comme on voudrait.
Dans notre cas, une spline est une fonction qui affiche un ensemble de paramètres d'entrée (points de contrôle) et la valeur de l'argument (prenant généralement des valeurs de 0 à 1) à un point sur un plan ou dans l'espace. La courbe résultante est l'ensemble des valeurs de la fonction spline pour .
À titre d'exemple, considérons lacourbe de Béziercubique, qui est donnée par l'équation suivante:


Courbe de Bézier cubique
La figure montre deux courbes de Bézier cubiques définies par quatre points (la courbe passe par deux d'entre eux, les deux autres définissent la courbure).
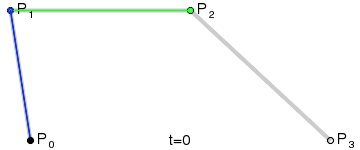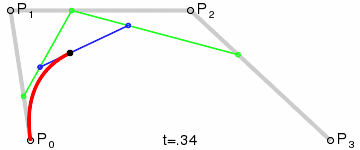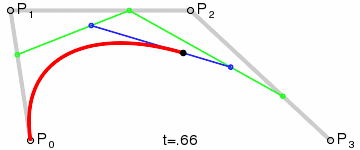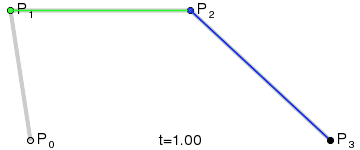
Animation de l'affichage du paramètre t sur un point de la courbe
Afin de construire un itinéraire plus complexe et variable à partir des sections de courbe, elles peuvent être connectées en une chaîne, laissant un point-lien commun:
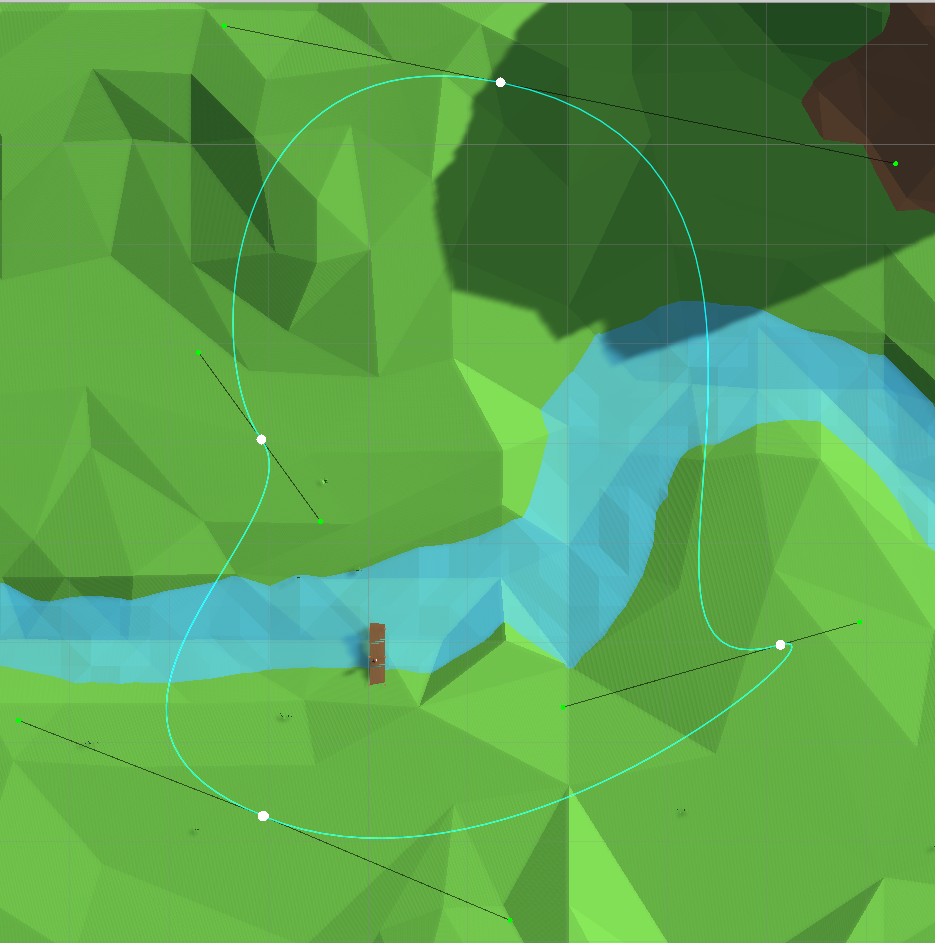
Spline par morceaux Nous avons
compris la tâche et le paramétrage de l'itinéraire, nous passons maintenant à la question principale. Pour que notre avion conventionnel se déplace le long de la route à vitesse constante, nous devons à tout moment être en mesure de calculer un point sur la courbe en fonction de la distance parcourue le long de cette courbe. , tout en n'ayant que la possibilité de calculer la position d'un point sur la courbe à partir de la valeur du paramètre (fonction ). C'est à ce stade que les difficultés commencent.
Ma première pensée a été de faire une cartographie linéaire et calculer partir de la valeur résultante - facile, peu coûteuse en calcul, en général, ce dont vous avez besoin.

Le problème avec cette méthode est immédiatement évident - en fait, la distance parcourue dépend de non linéaire, et pour s'en assurer, il suffit de disposer le long de l'itinéraire uniformément réparti points: points

répartis «uniformément» le long du trajet
Le plan ralentira dans certaines sections et accélérera dans d'autres, ce qui rend cette méthode de paramétrage de la courbe totalement inapplicable pour résoudre le problème décrit (le plan est choisi exclusivement comme exemple illustratif et le but de décrire son mouvement de manière physiquement correcte n'est a été poursuivi):

Visualiser le mauvais paramétrage de la courbe
Après avoir consulté le moteur de recherche, surstackoverflowetyoutube, j'ai découvert une deuxième façon de calculer , à savoir la représentation de la courbe sous forme de fonction linéaire par morceaux (calcul d'un ensemble de points équidistants les uns des autres le long de la courbe):
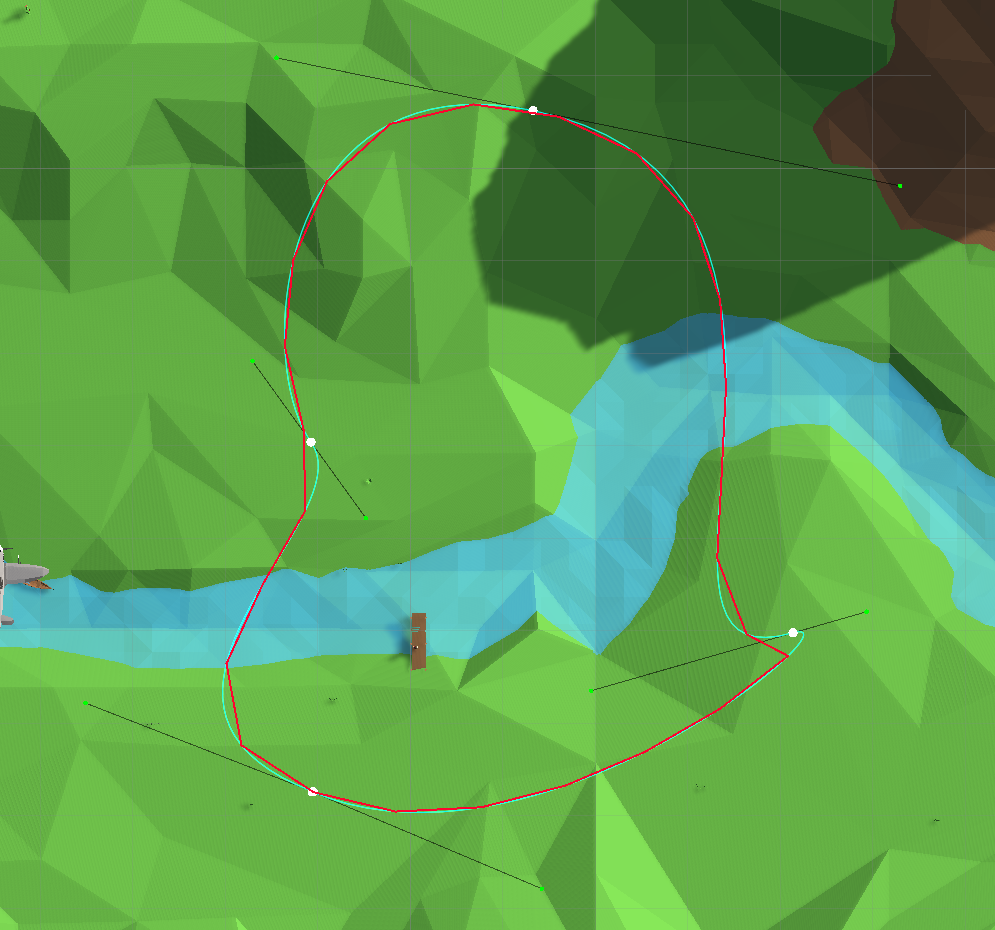
Représentation de la courbe comme une spline linéaire par morceaux
Cette procédure est itérative: un petit pas est fait , nous nous déplaçons le long d'une courbe avec elle, en additionnant la distance parcourue comme la longueur d'une spline linéaire par morceaux jusqu'à ce que la distance spécifiée soit couverte, après quoi le point est mémorisé, et le processus reprend.
Exemple de code
Une source
public Vector2[] CalculateEvenlySpacedPoints(float spacing, float resolution = 1)
{
List<Vector2> evenlySpacedPoints = new List<Vector2>();
evenlySpacedPoints.Add(points[0]);
Vector2 previousPoint = points[0];
float dstSinceLastEvenPoint = 0;
for (int segmentIndex = 0; segmentIndex < NumSegments; segmentIndex++)
{
Vector2[] p = GetPointsInSegment(segmentIndex);
float controlNetLength = Vector2.Distance(p[0], p[1]) + Vector2.Distance(p[1], p[2]) + Vector2.Distance(p[2], p[3]);
float estimatedCurveLength = Vector2.Distance(p[0], p[3]) + controlNetLength / 2f;
int divisions = Mathf.CeilToInt(estimatedCurveLength * resolution * 10);
float t = 0;
while (t <= 1)
{
t += 1f/divisions;
Vector2 pointOnCurve = Bezier.EvaluateCubic(p[0], p[1], p[2], p[3], t);
dstSinceLastEvenPoint += Vector2.Distance(previousPoint, pointOnCurve);
while (dstSinceLastEvenPoint >= spacing)
{
float overshootDst = dstSinceLastEvenPoint - spacing;
Vector2 newEvenlySpacedPoint = pointOnCurve + (previousPoint - pointOnCurve).normalized * overshootDst;
evenlySpacedPoints.Add(newEvenlySpacedPoint);
dstSinceLastEvenPoint = overshootDst;
previousPoint = newEvenlySpacedPoint;
}
previousPoint = pointOnCurve;
}
}
return evenlySpacedPoints.ToArray();
}Et, semble-t-il, le problème est résolu, car vous pouvez diviser l'itinéraire en plusieurs segments et apprécier la fluidité et la mesure avec laquelle l'objet se déplace, car le calcul d'un point sur une fonction linéaire par morceaux est une question simple et rapide. Mais cette approche a aussi des inconvénients assez évidents qui m'ont dérangé - une procédure assez coûteuse pour changer le pas de partition ou la géométrie de la courbe et la nécessité de trouver un équilibre entre précision (plus de consommation de mémoire) et économies de mémoire (l'itinéraire "cassé" devient plus perceptible).
En conséquence, j'ai continué à chercher et suis tombé sur un excellent article "Déplacement le long d'une courbe avec une vitesse spécifiée" , sur la base duquel un raisonnement supplémentaire est basé.
La valeur de la vitesse peut être calculée commeoù est une fonction spline. Pour résoudre le problème, vous devez trouver la fonction , où - la longueur de l'arc entre le point de départ et celui souhaité, et cette expression définit la relation entre et .
En utilisant la substitution de variable de différenciation, nous pouvons écrire
En tenant compte du fait que la vitesse est une quantité non négative, on obtient
parce que à la condition que le module du vecteur vitesse reste inchangé (en général,n'est pas égal à un, mais à une constante, mais pour la simplicité des calculs, nous prendrons cette constante égale à un).
Maintenant, nous obtenons le rapport entre et explicitement:
d'où la longueur totale de la courbe est évidemment calculé comme . En utilisant la formule résultante, il est possible, ayant la valeur de l'argument , calcule la longueur de l'arc jusqu'au point où cette valeurest affiché.
Nous nous intéressons à l'opération inverse, c'est-à-dire au calcul de la valeur de l'argument le long d'une longueur d'arc donnée :
Puisqu'il n'y a pas de méthode analytique générale pour trouver la fonction inverse, vous devrez rechercher une solution numérique. Nous dénotons Pour un donné , il est nécessaire de trouver une telle valeur auquel ... Ainsi, la tâche s'est transformée en tâche de trouver la racine de l'équation, que la méthode de Newton peut parfaitement gérer.
La méthode forme une suite d'approximations de la forme
Où
Calculer besoin de calculer , dont le calcul nécessite à son tour une intégration numérique.
Choixcomme une première approximation semble maintenant raisonnable (rappelez-vous la première approche pour résoudre le problème).
Ensuite, nous itérons en utilisant la méthode de Newton jusqu'à ce que l'erreur de solution devienne acceptable ou que le nombre d'itérations effectuées soit prohibitif.
Il y a un problème potentiel avec l'utilisation de la méthode standard de Newton. Une fonction - non décroissant, puisque son dérivé est non négatif. Si la seconde dérivée, alors la fonction est appelée convexe et la méthode de Newton dessus est garantie de converger vers la racine. Cependant, dans notre cas, peut s'avérer négatif, en raison de laquelle la méthode de Newton peut converger en dehors de la plage de définition ... L'auteur de l'article propose d'utiliser une modification de la méthode de Newton, qui, si le résultat de l'itération suivante par la méthode de Newton ne tombe pas dans l'intervalle courant délimitant la racine, sélectionne à la place le milieu de l'intervalle ( méthode de la dichotomie ). Quel que soit le résultat du calcul à l'itération actuelle, la plage est réduite, ce qui signifie que la méthode converge vers la racine.
Reste à choisir la méthode d'intégration numérique - j'ai utilisé les quadratures de la méthode de Gauss , car elle fournit un résultat assez précis à faible coût.
Code de fonction pour le calcul de t (s)
public float ArcLength(float t) => Integrate(x => TangentMagnitude(x), 0, t);
private float Parameter(float length)
{
float t = 0 + length / ArcLength(1);
float lowerBound = 0f;
float upperBound = 1f;
for (int i = 0; i < 100; ++i)
{
float f = ArcLength(t) - length;
if (Mathf.Abs(f) < 0.01f)
break;
float derivative = TangentMagnitude(t);
float candidateT = t - f / derivative;
if (f > 0)
{
upperBound = t;
if (candidateT <= 0)
t = (upperBound + lowerBound) / 2;
else
t = candidateT;
}
else
{
lowerBound = t;
if (candidateT >= 1)
t = (upperBound + lowerBound) / 2;
else
t = candidateT;
}
}
return t;
}
Code de fonction d'intégration numérique
private static readonly (float, float)[] CubicQuadrature =
{(-0.7745966F, 0.5555556F), (0, 0.8888889F), (0.7745966F, 0.5555556F)};
public static float Integrate(Func<float, float> f, in float lowerBound, in float uppedBound)
{
var sum = 0f;
foreach (var (arg, weight) in CubicQuadrature)
{
var t = Mathf.Lerp(lowerBound, uppedBound, Mathf.InverseLerp(-1, 1, arg));
sum += weight * f(t);
}
return sum * (upperBound - lowerBound) / 2;
}Ensuite, vous pouvez ajuster l'erreur de la méthode de Newton, choisir une méthode d'intégration numérique plus précise, mais le problème, en fait, est résolu - un algorithme de calcul de l'argument a été construit spline pour une longueur d'arc donnée. Pour combiner plusieurs sections de courbes en une seule et écrire une procédure de calcul généraliséevous pouvez stocker les longueurs de tous les segments et pré-calculer l'index du segment où vous souhaitez exécuter une procédure itérative à l'aide de la méthode Newton modifiée.
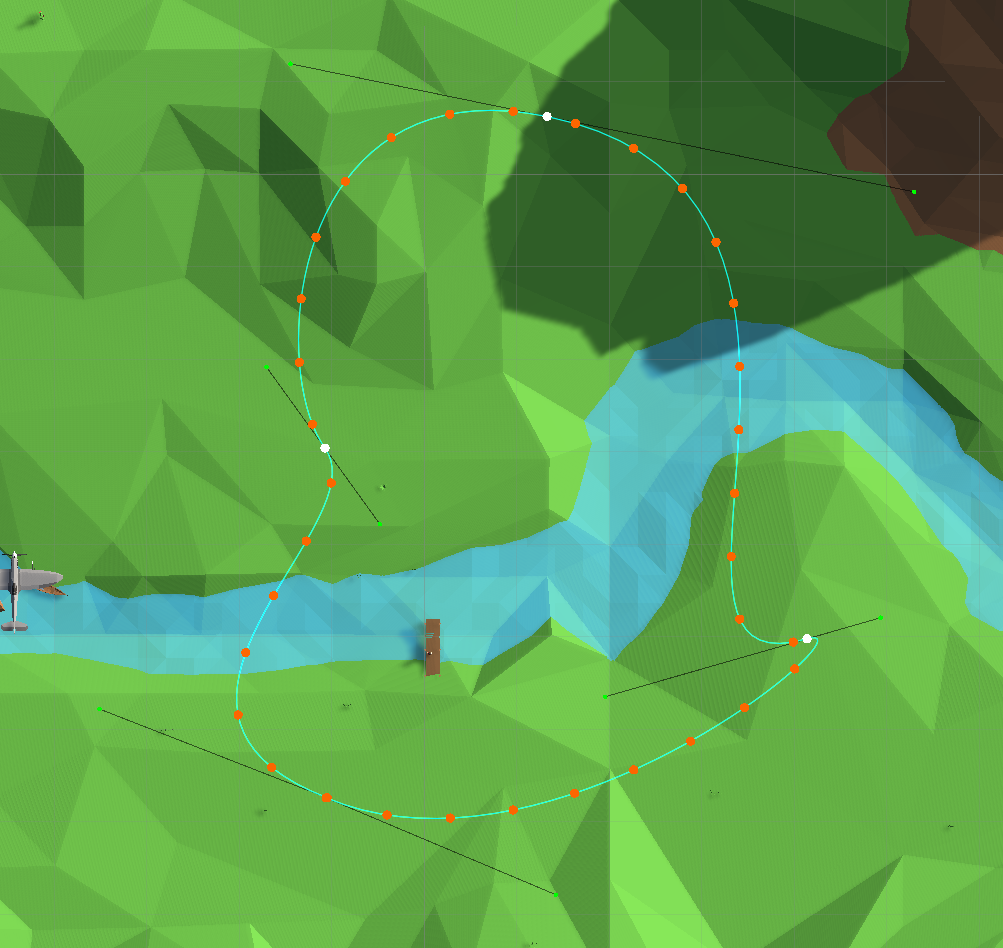
Points uniformément répartis le long de la trajectoire

Maintenant le plan se déplace uniformément
Ainsi, nous avons envisagé plusieurs façons de paramétrer la spline par rapport à la distance parcourue, dans l' article que j'ai utilisé comme source, en option, l'auteur propose de résoudre l'équation différentielle numériquement, mais, selon sa propre remarque, préfère la méthode modifiée Newton:
Je préfère l'approche de la méthode de Newton car généralement t peut être calculé plus rapidement qu'avec des solveurs d'équations différentielles.
En conclusion, je vais donner un tableau de temps pour calculer la position d'un point sur la courbe montrée dans les captures d'écran dans un thread sur un processeur i5-9600K:
| Nombre de calculs | Temps moyen, ms |
|---|---|
| 100 | 0,62 |
| 1000 | 6,24 |
| 10 000 | 69,01 |
| 100 000 | 672,81 |