Tout d'abord, nous allons nous familiariser brièvement avec les méthodes de parcours des graphiques, écrire le chemin d'accès réel, puis passer à la plus délicieuse: l'optimisation des performances et des coûts de mémoire. Idéalement, vous devriez développer une implémentation qui ne génère pas du tout de déchets lorsqu'elle est utilisée.
J'ai été étonné de constater qu'une recherche superficielle ne m'a pas donné une seule bonne implémentation de l'algorithme A * en C # sans utiliser de bibliothèques tierces (cela ne veut pas dire qu'il n'y en a pas). Il est donc temps de vous dégourdir les doigts!
J'attends un lecteur qui souhaite comprendre le travail des algorithmes de pathfinding, ainsi que des experts en algorithmes pour se familiariser avec la mise en œuvre et les méthodes de son optimisation.
Commençons!
Une excursion dans l'histoire
Un maillage bidimensionnel peut être représenté sous forme de graphe, où chacun des sommets a 8 arêtes:
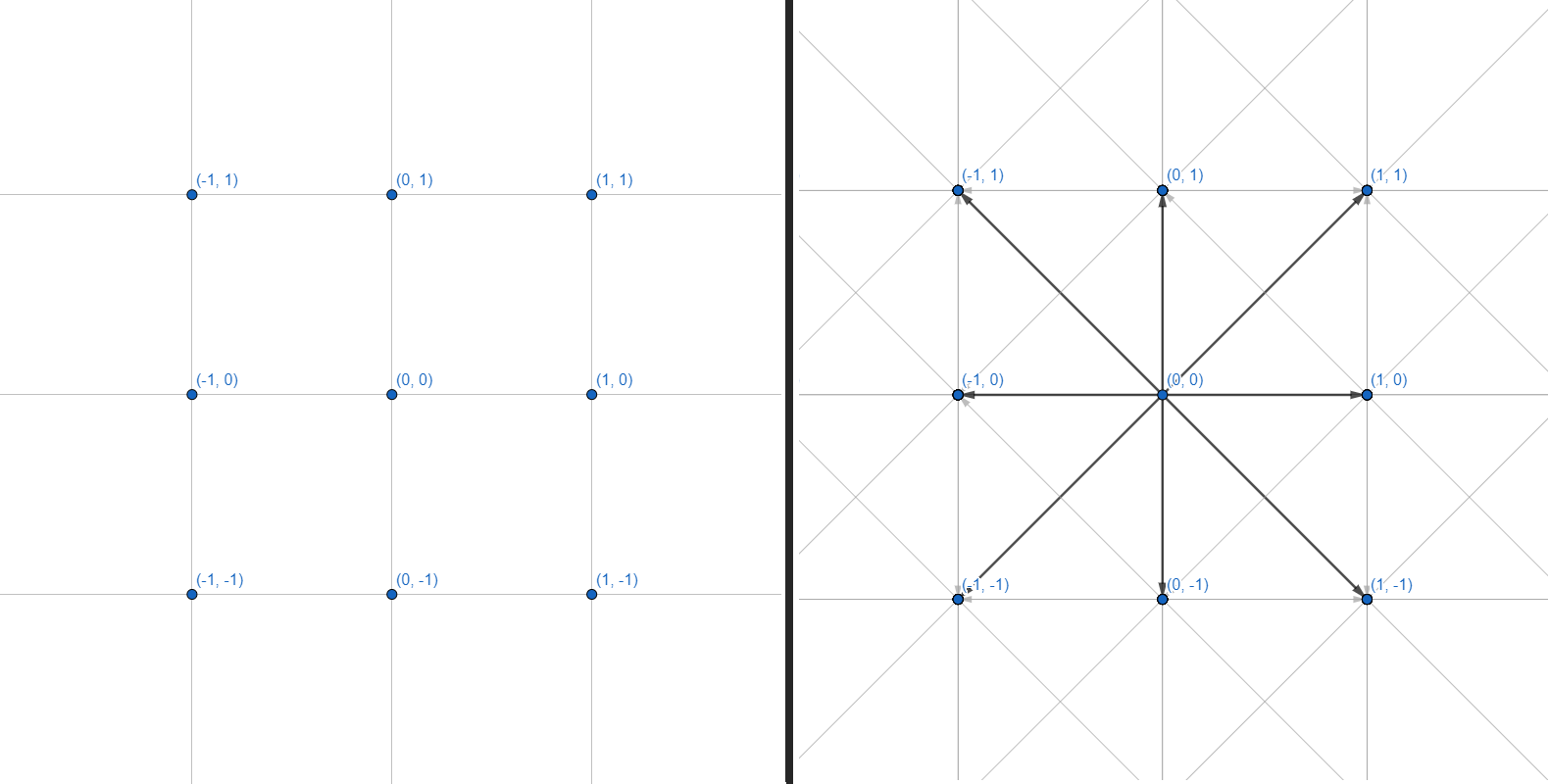
Nous travaillerons avec des graphes. Chaque sommet est une coordonnée entière. Chaque arête est une transition droite ou diagonale entre des coordonnées adjacentes. Nous ne ferons pas la grille de coordonnées et le calcul de la géométrie des obstacles - nous nous limiterons à une interface qui accepte plusieurs coordonnées en entrée et renvoie un ensemble de points pour construire un chemin:
public interface IPath
{
IReadOnlyCollection<Vector2Int> Calculate(Vector2Int start, Vector2Int target,
IReadOnlyCollection<Vector2Int> obstacles);
}Tout d'abord, considérons les méthodes existantes pour parcourir le graphe.
Recherche en profondeur
Le plus simple des algorithmes:
- Ajoutez tous les sommets non visités proches de celui en cours à la pile.
- Déplacez-vous vers le premier sommet de la pile.
- Si le sommet est celui souhaité, quittez le cycle. Si vous arrivez à une impasse, revenez en arrière.
- GOTO 1.
Cela ressemble à ceci:
, Node , .
private Node DFS(Node first, Node target)
{
List<Node> visited = new List<Node>();
Stack<Node> frontier = new Stack<Node>();
frontier.Push(first);
while (frontier.Count > 0)
{
var current = frontier.Pop();
visited.Add(current);
if (current == target)
return Node;
var neighbours = current.GenerateNeighbours();
foreach(var neighbour in neighbours)
if (!visited.Contains(neighbour))
frontier.Push(neighbour);
}
return default;
}, Node , .
Il est organisé au format LIFO ( Last in - First Out ), où les sommets nouvellement ajoutés sont analysés en premier. Chaque transition entre les sommets doit être surveillée afin de construire ensuite le chemin réel le long des transitions.
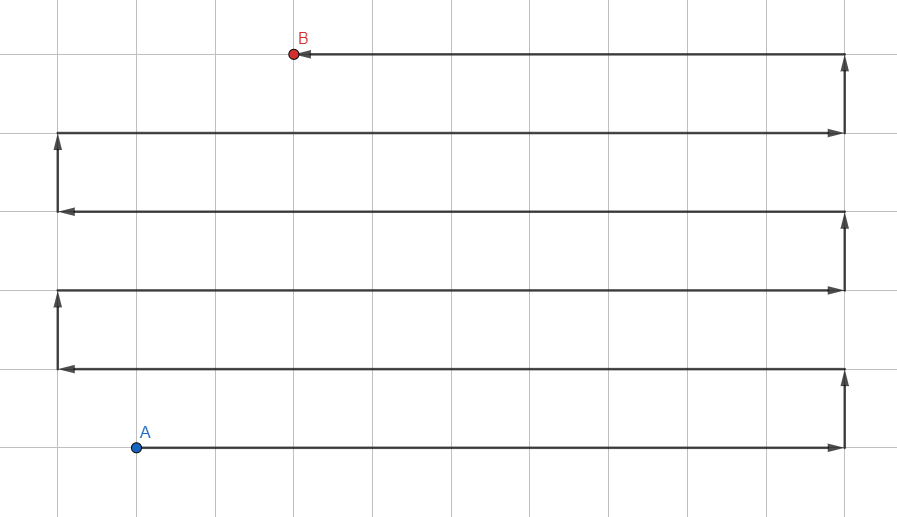
Cette approche ne retournera jamais (enfin, presque) le chemin le plus court puisqu'elle traite le graphe dans une direction aléatoire. Il est plus adapté aux petits graphiques afin de déterminer sans mal de tête s'il existe au moins un chemin vers le sommet souhaité (par exemple, si le lien souhaité est présent dans l'arbre technologique).
Dans le cas d'une grille de navigation et de graphes infinis, cette recherche ira à l'infini dans une direction et gaspillera des ressources de calcul, sans jamais atteindre le point souhaité. Ceci est résolu en limitant la zone dans laquelle l'algorithme opère. Nous lui faisons analyser uniquement les points qui ne sont pas plus loin que N pas de l'initial. Ainsi, lorsque l'algorithme atteint la frontière de la région, il se déplie et continue d'analyser les sommets dans le rayon spécifié.
Parfois, il est impossible de déterminer avec précision la zone, mais vous ne voulez pas définir la bordure au hasard. Une recherche itérative en profondeur d'abord vient à la rescousse :
- Définissez la zone minimale pour DFS.
- Lancer la recherche.
- Si le chemin n'est pas trouvé, augmentez la zone de recherche de 1.
- GOTO 2.
L'algorithme fonctionnera encore et encore, couvrant à chaque fois une zone plus grande, jusqu'à ce qu'il trouve enfin le point souhaité.
Cela peut sembler un gaspillage d'énergie de réexécuter l'algorithme à un rayon légèrement plus grand (de toute façon, la majeure partie de la zone a déjà été analysée à la dernière itération!), Mais non: le nombre de transitions entre les sommets croît géométriquement à chaque augmentation du rayon. Il sera beaucoup plus coûteux de prendre un rayon plus grand que nécessaire, que de marcher plusieurs fois le long de petits rayons.
Il est facile pour une telle recherche de resserrer une limite de minuterie: elle recherchera un chemin avec un rayon d'expansion exactement jusqu'à la fin du temps spécifié.
Première recherche en largeur
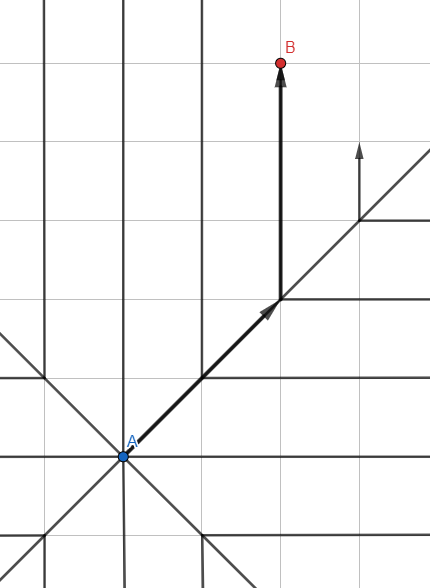
L'illustration peut ressembler à Jump Search - mais il s'agit de l' algorithme d'onde habituel , et les lignes représentent les chemins de propagation de recherche avec les points intermédiaires supprimés.
Contrairement à la recherche en profondeur en utilisant une pile (LIFO), prenons une file d'attente (FIFO) pour traiter les sommets:
- Ajoutez tous les voisins non visités à la file d'attente.
- Accédez au premier sommet de la file d'attente.
- Si le sommet est celui souhaité, quittez le cycle, sinon GOTO 1.
Cela ressemble à ceci:
, Node , .
private Node BFS(Node first, Node target)
{
List<Node> visited = new List<Node>();
Queue<Node> frontier = new Queue<Node>();
frontier.Enqueue(first);
while (frontier.Count > 0)
{
var current = frontier.Dequeue();
visited.Add(current);
if (current == target)
return Node;
var neighbours = current.GenerateNeighbours();
foreach(var neighbour in neighbours)
if (!visited.Contains(neighbour))
frontier.Enqueue(neighbour);
}
return default;
}, Node , .
Cette approche donne le chemin optimal , mais il y a un hic: puisque l'algorithme traite les sommets dans toutes les directions, il fonctionne très lentement sur de longues distances et des graphes avec une forte ramification. C'est juste notre cas.
Ici, la zone de fonctionnement de l'algorithme ne peut être limitée, car dans tous les cas il ne dépassera pas le rayon jusqu'au point souhaité. D'autres méthodes d'optimisation sont nécessaires.
UNE *
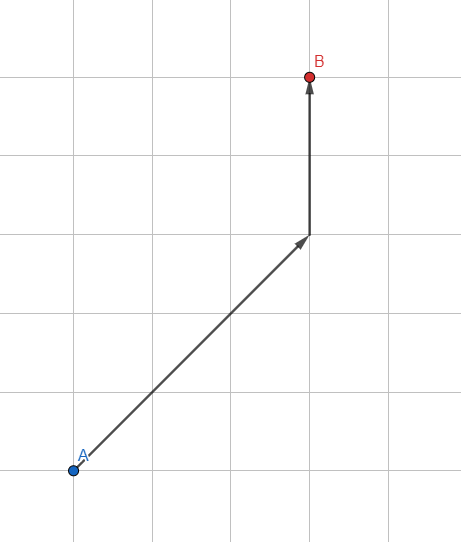
Modifions la recherche standard en largeur d'abord: nous n'utilisons pas une file d'attente normale pour stocker les sommets, mais une file d'attente triée basée sur l' heuristique - une estimation approximative du chemin attendu.
Comment estimer le chemin attendu? Le plus simple est la longueur du vecteur du sommet traité au point souhaité. Plus le vecteur est petit, plus le point est prometteur et plus il se rapproche du début de la file d'attente. L'algorithme donnera la priorité aux sommets qui se trouvent dans la direction du but.
Ainsi, chaque itération à l'intérieur de l'algorithme prendra un peu plus de temps en raison de calculs supplémentaires, mais en réduisant le nombre de sommets à analyser (seuls les plus prometteurs seront traités), nous obtenons une augmentation considérable de la vitesse de l'algorithme.
Mais il y a encore beaucoup de sommets traités. Trouver la longueur d'un vecteur est une opération coûteuse impliquant le calcul de la racine carrée. Par conséquent, nous utiliserons un calcul simplifié pour l'heuristique.
Créons un vecteur entier:
public readonly struct Vector2Int : IEquatable<Vector2Int>
{
private static readonly double Sqr = Math.Sqrt(2);
public Vector2Int(int x, int y)
{
X = x;
Y = y;
}
public int X { get; }
public int Y { get; }
/// <summary>
/// Estimated path distance without obstacles.
/// </summary>
public double DistanceEstimate()
{
int linearSteps = Math.Abs(Math.Abs(Y) - Math.Abs(X));
int diagonalSteps = Math.Max(Math.Abs(Y), Math.Abs(X)) - linearSteps;
return linearSteps + Sqr * diagonalSteps;
}
public static Vector2Int operator +(Vector2Int a, Vector2Int b)
=> new Vector2Int(a.X + b.X, a.Y + b.Y);
public static Vector2Int operator -(Vector2Int a, Vector2Int b)
=> new Vector2Int(a.X - b.X, a.Y - b.Y);
public static bool operator ==(Vector2Int a, Vector2Int b)
=> a.X == b.X && a.Y == b.Y;
public static bool operator !=(Vector2Int a, Vector2Int b)
=> !(a == b);
public bool Equals(Vector2Int other)
=> X == other.X && Y == other.Y;
public override bool Equals(object obj)
{
if (!(obj is Vector2Int))
return false;
var other = (Vector2Int) obj;
return X == other.X && Y == other.Y;
}
public override int GetHashCode()
=> HashCode.Combine(X, Y);
public override string ToString()
=> $"({X}, {Y})";
}Une structure standard pour stocker une paire de coordonnées. Ici, nous voyons la mise en cache de la racine carrée afin qu'elle ne puisse être calculée qu'une seule fois. L'interface IEquatable nous permettra de comparer des vecteurs entre eux sans avoir à traduire Vector2Int en objet et inversement. Cela accélérera considérablement notre algorithme et éliminera les allocations inutiles.
DistanceEstimate () est utilisé pour estimer la distance approximative de la cible en calculant le nombre de transitions droites et diagonales. Une autre manière est courante:
return Math.Max(Math.Abs(X), Math.Abs(Y))Cette option fonctionnera encore plus rapidement, mais cela est compensé par la faible précision de l'estimation de la distance diagonale.
Maintenant que nous avons un outil pour travailler avec les coordonnées, créons un objet qui représente le haut du graphique:
internal class PathNode
{
public PathNode(Vector2Int position, double traverseDist, double heuristicDist, PathNode parent)
{
Position = position;
TraverseDistance = traverseDist;
Parent = parent;
EstimatedTotalCost = TraverseDistance + heuristicDist;
}
public Vector2Int Position { get; }
public double TraverseDistance { get; }
public double EstimatedTotalCost { get; }
public PathNode Parent { get; }
}Dans Parent, nous enregistrerons le sommet précédent pour chaque nouveau: cela aidera à construire le chemin final par points. En plus des coordonnées, nous sauvegardons également la distance parcourue et le coût estimé du chemin afin de pouvoir ensuite sélectionner les sommets les plus prometteurs pour le traitement.
Cette classe demande des améliorations, mais nous y reviendrons plus tard. Pour l'instant, développons une méthode qui génère les voisins du sommet:
internal static class NodeExtensions
{
private static readonly (Vector2Int position, double cost)[] NeighboursTemplate = {
(new Vector2Int(1, 0), 1),
(new Vector2Int(0, 1), 1),
(new Vector2Int(-1, 0), 1),
(new Vector2Int(0, -1), 1),
(new Vector2Int(1, 1), Math.Sqrt(2)),
(new Vector2Int(1, -1), Math.Sqrt(2)),
(new Vector2Int(-1, 1), Math.Sqrt(2)),
(new Vector2Int(-1, -1), Math.Sqrt(2))
};
public static IEnumerable<PathNode> GenerateNeighbours(this PathNode parent, Vector2Int target)
{
foreach ((Vector2Int position, double cost) in NeighboursTemplate)
{
Vector2Int nodePosition = position + parent.Position;
double traverseDistance = parent.TraverseDistance + cost;
double heuristicDistance = (position - target).DistanceEstimate();
yield return new PathNode(nodePosition, traverseDistance, heuristicDistance, parent);
}
}
}NeighboursTemplate - un modèle prédéfini pour créer des voisins linéaires et diagonaux du point souhaité. Il prend également en compte le coût accru des transitions diagonales.
GenerateNeighbors - Un générateur qui traverse le NeighboursTemplate et retourne un nouveau sommet pour les huit côtés adjacents.
Il serait possible de pousser la fonctionnalité à l'intérieur du PathNode, mais cela ressemble à une légère violation de SRP. Et je ne veux pas non plus ajouter de fonctionnalités tierces à l'intérieur de l'algorithme lui-même: nous garderons les classes aussi compactes que possible.
Il est temps de s'attaquer à la principale classe de recherche de chemin!
public class Path
{
private readonly List<PathNode> frontier = new List<PathNode>();
private readonly List<Vector2Int> ignoredPositions = new List<Vector2Int>();
public IReadOnlyCollection<Vector2Int> Calculate(Vector2Int start, Vector2Int target,
IReadOnlyCollection<Vector2Int> obstacles) {...}
private bool GenerateNodes(Vector2Int start, Vector2Int target,
IEnumerable<Vector2Int> obstacles, out PathNode node)
{
frontier.Clear();
ignoredPositions.Clear();
ignoredPositions.AddRange(obstacles);
// Add starting point.
frontier.Add(new PathNode(start, 0, 0, null));
while (frontier.Any())
{
// Find node with lowest estimated cost.
var lowest = frontier.Min(a => a.EstimatedTotalCost);
PathNode current = frontier.First(a => a.EstimatedTotalCost == lowest);
ignoredPositions.Add(current.Position);
if (current.Position.Equals(target))
{
node = current;
return true;
}
GenerateFrontierNodes(current, target);
}
// All nodes analyzed - no path detected.
node = null;
return false;
}
private void GenerateFrontierNodes(PathNode parent, Vector2Int target)
{
foreach (PathNode newNode in parent.GenerateNeighbours(target))
{
// Position is already checked or occupied by an obstacle.
if (ignoredPositions.Contains(newNode.Position)) continue;
// Node is not present in queue.
var node = frontier.FirstOrDefault(a => a.Position == newNode.Position);
if (node == null)
frontier.Add(newNode);
// Node is present in queue and new optimal path is detected.
else if (newNode.TraverseDistance < node.TraverseDistance)
{
frontier.Remove(node);
frontier.Add(newNode);
}
}
}
}GenerateNodes fonctionne avec deux collections: frontier, qui contient une file d'attente de sommets à analyser, et ignoredPositions, auxquelles sont ajoutés des sommets déjà traités.
Chaque itération de la boucle trouve le sommet le plus prometteur, vérifie si nous avons atteint le point final et génère de nouveaux voisins pour ce sommet.
Et toute cette beauté s'inscrit dans 50 lignes.
Il reste à implémenter l'interface:
public IReadOnlyCollection<Vector2Int> Calculate(Vector2Int start, Vector2Int target,
IReadOnlyCollection<Vector2Int> obstacles)
{
if (!GenerateNodes(start, target, obstacles, out PathNode node))
return Array.Empty<Vector2Int>();
var output = new List<Vector2Int>();
while (node.Parent != null)
{
output.Add(node.Position);
node = node.Parent;
}
output.Add(start);
return output.AsReadOnly();
}GenerateNodes nous renvoie le sommet final, et puisque nous avons écrit un voisin parent à chacun d'eux, il suffit de parcourir tous les parents jusqu'au sommet initial - et nous obtenons le chemin le plus court. Tout va bien!
Ou pas?
Optimisation des algorithmes
1. PathNode
Commençons simplement. Simplifions PathNode:
internal readonly struct PathNode
{
public PathNode(Vector2Int position, Vector2Int target, double traverseDistance)
{
Position = position;
TraverseDistance = traverseDistance;
double heuristicDistance = (position - target).DistanceEstimate();
EstimatedTotalCost = traverseDistance + heuristicDistance;
}
public Vector2Int Position { get; }
public double TraverseDistance { get; }
public double EstimatedTotalCost { get; }
}Il s'agit d'un wrapper de données commun qui est également très souvent créé. Il n'y a aucune raison d'en faire une classe et de charger de la mémoire à chaque fois que nous en écrivons un nouveau . Par conséquent, nous utiliserons struct.
Mais il y a un problème: les structures ne peuvent pas contenir de références circulaires à leur propre type. Ainsi, au lieu de stocker le Parent à l'intérieur du PathNode, nous avons besoin d'un autre moyen de suivre la construction des chemins entre les sommets. C'est facile - ajoutons une nouvelle collection à la classe Path:
private readonly Dictionary<Vector2Int, Vector2Int> links;Et nous modifions légèrement la génération des voisins:
private void GenerateFrontierNodes(PathNode parent, Vector2Int target)
{
foreach (PathNode newNode in parent.GenerateNeighbours(target))
{
// Position is already checked or occupied by an obstacle.
if (ignoredPositions.Contains(newNode.Position)) continue;
// Node is not present in queue.
if (!frontier.TryGet(newNode.Position, out PathNode existingNode))
{
frontier.Enqueue(newNode);
links[newNode.Position] = parent.Position; // Add link to dictionary.
}
// Node is present in queue and new optimal path is detected.
else if (newNode.TraverseDistance < existingNode.TraverseDistance)
{
frontier.Modify(newNode);
links[newNode.Position] = parent.Position; // Add link to dictionary.
}
}
}Au lieu d'écrire le parent sur le sommet lui-même, nous écrivons la transition vers le dictionnaire. En prime, le dictionnaire peut fonctionner directement avec Vector2Int, et non avec PathNode, car nous n'avons besoin que de coordonnées et rien d'autre.
La génération du résultat dans Calculate est également simplifiée:
public IReadOnlyCollection<Vector2Int> Calculate(Vector2Int start, Vector2Int target,
IReadOnlyCollection<Vector2Int> obstacles)
{
if (!GenerateNodes(start, target, obstacles))
return Array.Empty<Vector2Int>();
var output = new List<Vector2Int> {target};
while (links.TryGetValue(target, out target))
output.Add(target);
return output.AsReadOnly();
}2. NodeExtensions
Ensuite, parlons de la génération de voisins. IEnumerable, malgré tous ses avantages, génère une triste quantité de déchets dans de nombreuses situations. Débarrassons-nous-en:
internal static class NodeExtensions
{
private static readonly (Vector2Int position, double cost)[] NeighboursTemplate = {
(new Vector2Int(1, 0), 1),
(new Vector2Int(0, 1), 1),
(new Vector2Int(-1, 0), 1),
(new Vector2Int(0, -1), 1),
(new Vector2Int(1, 1), Math.Sqrt(2)),
(new Vector2Int(1, -1), Math.Sqrt(2)),
(new Vector2Int(-1, 1), Math.Sqrt(2)),
(new Vector2Int(-1, -1), Math.Sqrt(2))
};
public static void Fill(this PathNode[] buffer, PathNode parent, Vector2Int target)
{
int i = 0;
foreach ((Vector2Int position, double cost) in NeighboursTemplate)
{
Vector2Int nodePosition = position + parent.Position;
double traverseDistance = parent.TraverseDistance + cost;
buffer[i++] = new PathNode(nodePosition, target, traverseDistance);
}
}
}Maintenant, notre méthode d'extension n'est pas un générateur: elle ne remplit que le tampon qui lui est passé en argument. Le tampon est stocké comme une autre collection dans le chemin:
private const int MaxNeighbours = 8;
private readonly PathNode[] neighbours = new PathNode[MaxNeighbours];Et il est utilisé comme ceci:
neighbours.Fill(parent, target);
foreach(var neighbour in neighbours)
{
// ...3. HashSet
Au lieu d'utiliser List, utilisons HashSet:
private readonly HashSet<Vector2Int> ignoredPositions;Elle est beaucoup plus efficace lorsque vous travaillez avec de grandes collections, la méthode ignoredPositions.Contains () est très gourmande en ressources en raison de la fréquence des appels. Un simple changement de type de collection donnera une amélioration notable des performances.
4. BinaryHeap
Il y a un endroit dans notre implémentation qui ralentit l'algorithme dix fois:
// Find node with lowest estimated cost.
var lowest = frontier.Min(a => a.EstimatedTotalCost);
PathNode current = frontier.First(a => a.EstimatedTotalCost == lowest);La liste elle-même est un mauvais choix et l'utilisation de Linq aggrave les choses.
Idéalement, nous voulons une collection avec:
- Tri automatique.
- Faible croissance de complexité asymptotique.
- Opération d'insertion rapide.
- Opération de retrait rapide.
- Navigation facile à travers les éléments.
SortedSet peut sembler une bonne option, mais il ne sait pas comment contenir les doublons. Si nous écrivons le tri par EstimatedTotalCost, alors tous les sommets avec le même prix (mais des coordonnées différentes!) Seront éliminés. Dans les zones ouvertes avec un petit nombre d'obstacles, ce n'est pas effrayant, en plus cela accélérera l'algorithme, mais dans des labyrinthes étroits, le résultat sera des itinéraires inexacts et des résultats faux négatifs.
Nous allons donc implémenter notre collection - le tas binaire ! La mise en œuvre classique répond à 4 exigences sur 5, et une petite modification rendra cette collection idéale pour notre cas.
La collection est un arbre partiellement trié, avec la complexité des opérations d'insertion et de suppression égale à log (n) .
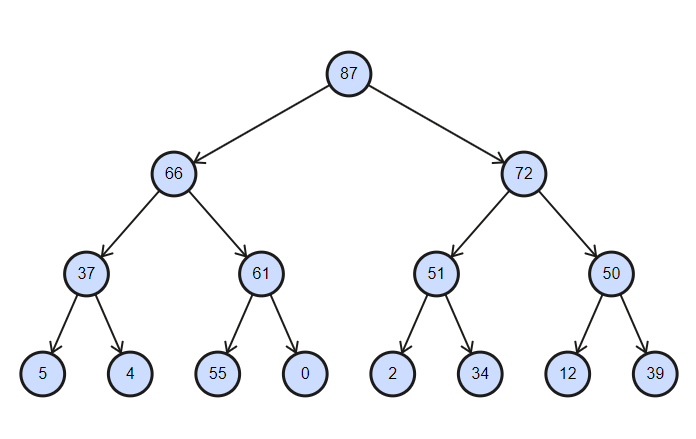
Tas binaire trié par ordre décroissant
internal interface IBinaryHeap<in TKey, T>
{
void Enqueue(T item);
T Dequeue();
void Clear();
bool TryGet(TKey key, out T value);
void Modify(T value);
int Count { get; }
}Écrivons la partie facile:
internal class BinaryHeap : IBinaryHeap<Vector2Int, PathNode>
{
private readonly IDictionary<Vector2Int, int> map;
private readonly IList<PathNode> collection;
private readonly IComparer<PathNode> comparer;
public BinaryHeap(IComparer<PathNode> comparer)
{
this.comparer = comparer;
collection = new List<PathNode>();
map = new Dictionary<Vector2Int, int>();
}
public int Count => collection.Count;
public void Clear()
{
collection.Clear();
map.Clear();
}
// ...
}Nous utiliserons IComparer pour le tri personnalisé des sommets. IList est en fait le magasin de vertex avec lequel nous allons travailler. Nous avons besoin d'IDictionary pour garder une trace des indices des sommets pour leur suppression rapide (l'implémentation standard du tas binaire nous permet de travailler facilement avec uniquement l'élément supérieur).
Ajoutons un élément:
public void Enqueue(PathNode item)
{
collection.Add(item);
int i = collection.Count - 1;
map[item.Position] = i;
// Sort nodes from bottom to top.
while(i > 0)
{
int j = (i - 1) / 2;
if (comparer.Compare(collection[i], collection[j]) <= 0)
break;
Swap(i, j);
i = j;
}
}
private void Swap(int i, int j)
{
PathNode temp = collection[i];
collection[i] = collection[j];
collection[j] = temp;
map[collection[i].Position] = i;
map[collection[j].Position] = j;
}Chaque nouvel élément est ajouté à la dernière cellule de l'arbre, après quoi il est partiellement trié de bas en haut: par nœuds du nouvel élément à la racine, jusqu'à ce que le plus petit élément soit aussi haut que possible. Puisque la collection entière n'est pas triée, mais seulement les nœuds intermédiaires entre le haut et le dernier, l'opération a le journal de complexité (n) .
Obtenir un article:
public PathNode Dequeue()
{
if (collection.Count == 0) return default;
PathNode result = collection.First();
RemoveRoot();
map.Remove(result.Position);
return result;
}
private void RemoveRoot()
{
collection[0] = collection.Last();
map[collection[0].Position] = 0;
collection.RemoveAt(collection.Count - 1);
// Sort nodes from top to bottom.
var i = 0;
while(true)
{
int largest = LargestIndex(i);
if (largest == i)
return;
Swap(i, largest);
i = largest;
}
}
private int LargestIndex(int i)
{
int leftInd = 2 * i + 1;
int rightInd = 2 * i + 2;
int largest = i;
if (leftInd < collection.Count
&& comparer.Compare(collection[leftInd], collection[largest]) > 0)
largest = leftInd;
if (rightInd < collection.Count
&& comparer.Compare(collection[rightInd], collection[largest]) > 0)
largest = rightInd;
return largest;
}Par analogie avec l'ajout: l'élément racine est supprimé et le dernier est remis à sa place. Ensuite, un tri partiel de haut en bas permute les éléments de sorte que le plus petit soit en haut.
Après cela, nous implémentons la recherche d'un élément et le modifions:
public bool TryGet(Vector2Int key, out PathNode value)
{
if (!map.TryGetValue(key, out int index))
{
value = default;
return false;
}
value = collection[index];
return true;
}
public void Modify(PathNode value)
{
if (!map.TryGetValue(value.Position, out int index))
throw new KeyNotFoundException(nameof(value));
collection[index] = value;
}Il n'y a rien de compliqué ici: on recherche l'index de l'élément à travers le dictionnaire, après quoi on y accède directement.
Version générique du tas:
internal class BinaryHeap<TKey, T> : IBinaryHeap<TKey, T> where TKey : IEquatable<TKey>
{
private readonly IDictionary<TKey, int> map;
private readonly IList<T> collection;
private readonly IComparer<T> comparer;
private readonly Func<T, TKey> lookupFunc;
public BinaryHeap(IComparer<T> comparer, Func<T, TKey> lookupFunc, int capacity)
{
this.comparer = comparer;
this.lookupFunc = lookupFunc;
collection = new List<T>(capacity);
map = new Dictionary<TKey, int>(capacity);
}
public int Count => collection.Count;
public void Enqueue(T item)
{
collection.Add(item);
int i = collection.Count - 1;
map[lookupFunc(item)] = i;
while(i > 0)
{
int j = (i - 1) / 2;
if (comparer.Compare(collection[i], collection[j]) <= 0)
break;
Swap(i, j);
i = j;
}
}
public T Dequeue()
{
if (collection.Count == 0) return default;
T result = collection.First();
RemoveRoot();
map.Remove(lookupFunc(result));
return result;
}
public void Clear()
{
collection.Clear();
map.Clear();
}
public bool TryGet(TKey key, out T value)
{
if (!map.TryGetValue(key, out int index))
{
value = default;
return false;
}
value = collection[index];
return true;
}
public void Modify(T value)
{
if (!map.TryGetValue(lookupFunc(value), out int index))
throw new KeyNotFoundException(nameof(value));
collection[index] = value;
}
private void RemoveRoot()
{
collection[0] = collection.Last();
map[lookupFunc(collection[0])] = 0;
collection.RemoveAt(collection.Count - 1);
var i = 0;
while(true)
{
int largest = LargestIndex(i);
if (largest == i)
return;
Swap(i, largest);
i = largest;
}
}
private void Swap(int i, int j)
{
T temp = collection[i];
collection[i] = collection[j];
collection[j] = temp;
map[lookupFunc(collection[i])] = i;
map[lookupFunc(collection[j])] = j;
}
private int LargestIndex(int i)
{
int leftInd = 2 * i + 1;
int rightInd = 2 * i + 2;
int largest = i;
if (leftInd < collection.Count && comparer.Compare(collection[leftInd], collection[largest]) > 0) largest = leftInd;
if (rightInd < collection.Count && comparer.Compare(collection[rightInd], collection[largest]) > 0) largest = rightInd;
return largest;
}
}Maintenant, notre recherche de chemin a une vitesse décente et il n'y a presque plus de génération de déchets. La finition est proche!
5. Collections réutilisables
L'algorithme est en cours de développement en vue de pouvoir l'appeler des dizaines de fois par seconde. La génération de tout garbage est catégoriquement inacceptable: un garbage collector chargé peut (et va!) Provoquer des baisses périodiques des performances.
Toutes les collections, à l'exception de la sortie, sont déjà déclarées une fois lors de la création de la classe, et la dernière y est également ajoutée:
private const int MaxNeighbours = 8;
private readonly PathNode[] neighbours = new PathNode[MaxNeighbours];
private readonly IBinaryHeap<Vector2Int, PathNode> frontier;
private readonly HashSet<Vector2Int> ignoredPositions;
private readonly IList<Vector2Int> output;
private readonly IDictionary<Vector2Int, Vector2Int> links;
public Path()
{
var comparer = Comparer<PathNode>.Create((a, b) => b.EstimatedTotalCost.CompareTo(a.EstimatedTotalCost));
frontier = new BinaryHeap(comparer);
ignoredPositions = new HashSet<Vector2Int>();
output = new List<Vector2Int>();
links = new Dictionary<Vector2Int, Vector2Int>();
}La méthode publique prend la forme suivante:
public IReadOnlyCollection<Vector2Int> Calculate(Vector2Int start, Vector2Int target,
IReadOnlyCollection<Vector2Int> obstacles)
{
if (!GenerateNodes(start, target, obstacles))
return Array.Empty<Vector2Int>();
output.Clear();
output.Add(target);
while (links.TryGetValue(target, out target))
output.Add(target);
return output.AsReadOnly();
}Et il ne s'agit pas seulement de créer des collections! Les collections modifient dynamiquement leur capacité lorsqu'elles sont remplies; si le chemin est long, le redimensionnement se produira des dizaines de fois. C'est très gourmand en mémoire. Lorsque nous effaçons les collections et les réutilisons sans en déclarer de nouvelles, elles conservent leur capacité. La première construction de chemin créera beaucoup de déchets lors de l'initialisation des collections et de la modification de leurs capacités, mais les appels suivants fonctionneront correctement sans aucune allocation (à condition que la longueur de chaque chemin calculé soit plus ou moins la même sans distorsions brusques). D'où le point suivant:
6. (Bonus) Annonce de la taille des collections
Un certain nombre de questions se posent immédiatement:
- Est-il préférable de décharger la charge sur le constructeur de la classe Path ou de la laisser lors du premier appel au pathfinder?
- Quelle capacité pour nourrir les collections?
- Est-il moins coûteux d'annoncer une plus grande capacité tout de suite ou de laisser la collection s'agrandir d'elle-même?
Le troisième peut être répondu tout de suite: si nous avons des centaines et des milliers de cellules pour trouver un chemin, il sera certainement moins cher d'attribuer immédiatement une certaine taille à nos collections.
Il est plus difficile de répondre aux deux autres questions. La réponse à ces problèmes doit être déterminée empiriquement pour chaque cas d'utilisation. Si nous décidons toujours de déplacer la charge dans le constructeur, il est temps d'ajouter une limite au nombre d'étapes à notre algorithme:
public Path(int maxSteps)
{
this.maxSteps = maxSteps;
var comparer = Comparer<PathNode>.Create((a, b) => b.EstimatedTotalCost.CompareTo(a.EstimatedTotalCost));
frontier = new BinaryHeap(comparer, maxSteps);
ignoredPositions = new HashSet<Vector2Int>(maxSteps);
output = new List<Vector2Int>(maxSteps);
links = new Dictionary<Vector2Int, Vector2Int>(maxSteps);
}Dans GenerateNodes, corrigez la boucle:
var step = 0;
while (frontier.Count > 0 && step++ <= maxSteps)
{
// ...
}Ainsi, les collections se voient immédiatement attribuer une capacité égale au chemin maximum. Certaines collections contiennent non seulement les nœuds traversés, mais aussi leurs voisins: pour de telles collections, vous pouvez utiliser une capacité 4 à 5 fois supérieure à celle spécifiée.
Cela peut paraître un peu trop, mais pour des chemins proches du maximum déclaré, l'attribution de la taille des collections consomme de moitié à trois fois moins de mémoire qu'une expansion dynamique. En revanche, si vous attribuez de très grandes valeurs à la valeur maxSteps et générez des chemins courts, une telle innovation ne fera que nuire. Oh, et vous ne devriez pas essayer d'utiliser int.MaxValue!
La solution optimale serait de créer deux constructeurs, dont l'un définit la capacité initiale des collections. Ensuite, notre classe peut être utilisée dans les deux cas sans la modifier.
Que pouvez vous faire d'autre?
- .
- XML-.
- GetHashCode Vector2Int. , , , .
- , . .
- IComparable PathNode EqualityComparer. .
- : , . , , .
- Changez la signature de la méthode dans notre interface pour mieux refléter son essence:
bool Calculate(Vector2Int start, Vector2Int target, IReadOnlyCollection<Vector2Int> obstacles, out IReadOnlyCollection<Vector2Int> path);
Ainsi, la méthode montre clairement la logique de son fonctionnement, alors que la méthode originale aurait dû être appelée comme ceci: CalculateOrReturnEmpty .
La version finale de la classe Path:
/// <summary>
/// Reusable A* path finder.
/// </summary>
public class Path : IPath
{
private const int MaxNeighbours = 8;
private readonly PathNode[] neighbours = new PathNode[MaxNeighbours];
private readonly int maxSteps;
private readonly IBinaryHeap<Vector2Int, PathNode> frontier;
private readonly HashSet<Vector2Int> ignoredPositions;
private readonly List<Vector2Int> output;
private readonly IDictionary<Vector2Int, Vector2Int> links;
/// <summary>
/// Creation of new path finder.
/// </summary>
/// <exception cref="ArgumentOutOfRangeException"></exception>
public Path(int maxSteps = int.MaxValue, int initialCapacity = 0)
{
if (maxSteps <= 0)
throw new ArgumentOutOfRangeException(nameof(maxSteps));
if (initialCapacity < 0)
throw new ArgumentOutOfRangeException(nameof(initialCapacity));
this.maxSteps = maxSteps;
var comparer = Comparer<PathNode>.Create((a, b) => b.EstimatedTotalCost.CompareTo(a.EstimatedTotalCost));
frontier = new BinaryHeap<Vector2Int, PathNode>(comparer, a => a.Position, initialCapacity);
ignoredPositions = new HashSet<Vector2Int>(initialCapacity);
output = new List<Vector2Int>(initialCapacity);
links = new Dictionary<Vector2Int, Vector2Int>(initialCapacity);
}
/// <summary>
/// Calculate a new path between two points.
/// </summary>
/// <exception cref="ArgumentNullException"></exception>
public bool Calculate(Vector2Int start, Vector2Int target,
IReadOnlyCollection<Vector2Int> obstacles,
out IReadOnlyCollection<Vector2Int> path)
{
if (obstacles == null)
throw new ArgumentNullException(nameof(obstacles));
if (!GenerateNodes(start, target, obstacles))
{
path = Array.Empty<Vector2Int>();
return false;
}
output.Clear();
output.Add(target);
while (links.TryGetValue(target, out target)) output.Add(target);
path = output;
return true;
}
private bool GenerateNodes(Vector2Int start, Vector2Int target, IReadOnlyCollection<Vector2Int> obstacles)
{
frontier.Clear();
ignoredPositions.Clear();
links.Clear();
frontier.Enqueue(new PathNode(start, target, 0));
ignoredPositions.UnionWith(obstacles);
var step = 0;
while (frontier.Count > 0 && step++ <= maxSteps)
{
PathNode current = frontier.Dequeue();
ignoredPositions.Add(current.Position);
if (current.Position.Equals(target)) return true;
GenerateFrontierNodes(current, target);
}
// All nodes analyzed - no path detected.
return false;
}
private void GenerateFrontierNodes(PathNode parent, Vector2Int target)
{
neighbours.Fill(parent, target);
foreach (PathNode newNode in neighbours)
{
// Position is already checked or occupied by an obstacle.
if (ignoredPositions.Contains(newNode.Position)) continue;
// Node is not present in queue.
if (!frontier.TryGet(newNode.Position, out PathNode existingNode))
{
frontier.Enqueue(newNode);
links[newNode.Position] = parent.Position;
}
// Node is present in queue and new optimal path is detected.
else if (newNode.TraverseDistance < existingNode.TraverseDistance)
{
frontier.Modify(newNode);
links[newNode.Position] = parent.Position;
}
}
}
}Lien vers le code source