Les mathématiciens essaient depuis longtemps de s'habituer au fait que certains problèmes, en principe, ne peuvent pas être résolus

Nous aimons dire que tout est possible. Dans le livre de Jaster Norton "Cute and the Magic Booth", le roi refuse de dire à Milo que son objectif est inaccessible, car "beaucoup devient possible si vous ne savez pas que c'est impossible" [ bien que ce soient les mots d'autres personnages du livre / env. trad. ]. Mais dans le monde réel, certaines choses sont vraiment impossibles, et nous pouvons le prouver avec les mathématiques.
Les gens utilisent le terme «impossible» de différentes manières. Il ne peut décrire que les choses improbables, comme trouver deux paquets identiques de cartes mélangées. Il peut décrire des tâches qui sont presque impossibles en raison du manque de temps, d'espace ou de ressources, telles que la réécriture manuelle de l'ensemble de la Bibliothèque du Congrès. Des dispositifs tels que les machines à mouvement perpétuel sont physiquement impossibles, car leur existence contredirait notre compréhension de la physique.
L'impossibilité mathématique est différente. Nous partons d'hypothèses sans ambiguïté, et en utilisant le raisonnement mathématique et la logique, nous concluons que certains résultats sont impossibles. Aucune chance, persévérance, temps ou compétence ne rendront la tâche réalisable. L'histoire des mathématiques regorge de preuves d'impossibilité. Beaucoup d'entre eux sont considérés comme les résultats les plus remarquables des mathématiques. Mais ce ne fut pas toujours ainsi.
La punition, peut-être la toute première preuve d'impossibilité, était sévère. Les historiens le croient au 5ème siècle avant JC. Hippase de Metapont, un adepte de Pythagore, a découvert qu'il était impossible de trouver un segment de ligne qui pourrait mesurer à la fois la longueur des côtés et la longueur diagonale d'un pentagone régulier. Aujourd'hui, nous disons que la longueur de la diagonale d'un pentagone régulier de longueur de côté 1 est le nombre d'or, ϕ = 1/2 (1 + √5) - est un nombre irrationnel. La découverte d'Hippas était un défi au credo pythagoricien, "tout est numéro", alors les légendes disent qu'Hippase a été soit noyé dans la mer, soit simplement expulsé des rangs des Pythagoriciens.
Plus d'un siècle plus tard, Euclide a élevé la ligne et le cercle en tant que courbes fondamentales de la géométrie. Par la suite, de nombreuses générations de géomètres ont dessiné toutes sortes de choses - diviser des angles, dessiner des perpendiculaires, etc. - uniquement à l'aide de boussoles et d'une règle. Cependant, certaines structures, qui semblaient simples, déroutaient les géomètres grecs, ont acquis de ce fait un statut mythique et ont agacé les mathématiciens pendant plus de 2000 ans. Ce sont les problèmes de la division d'un angle arbitraire en trois parties, de la construction du côté d'un cube dont le volume est le double du volume du volume donné, de la construction de tous les polygones réguliers et de la construction d'un carré d'une aire égale à l'aire d'un cercle donné.
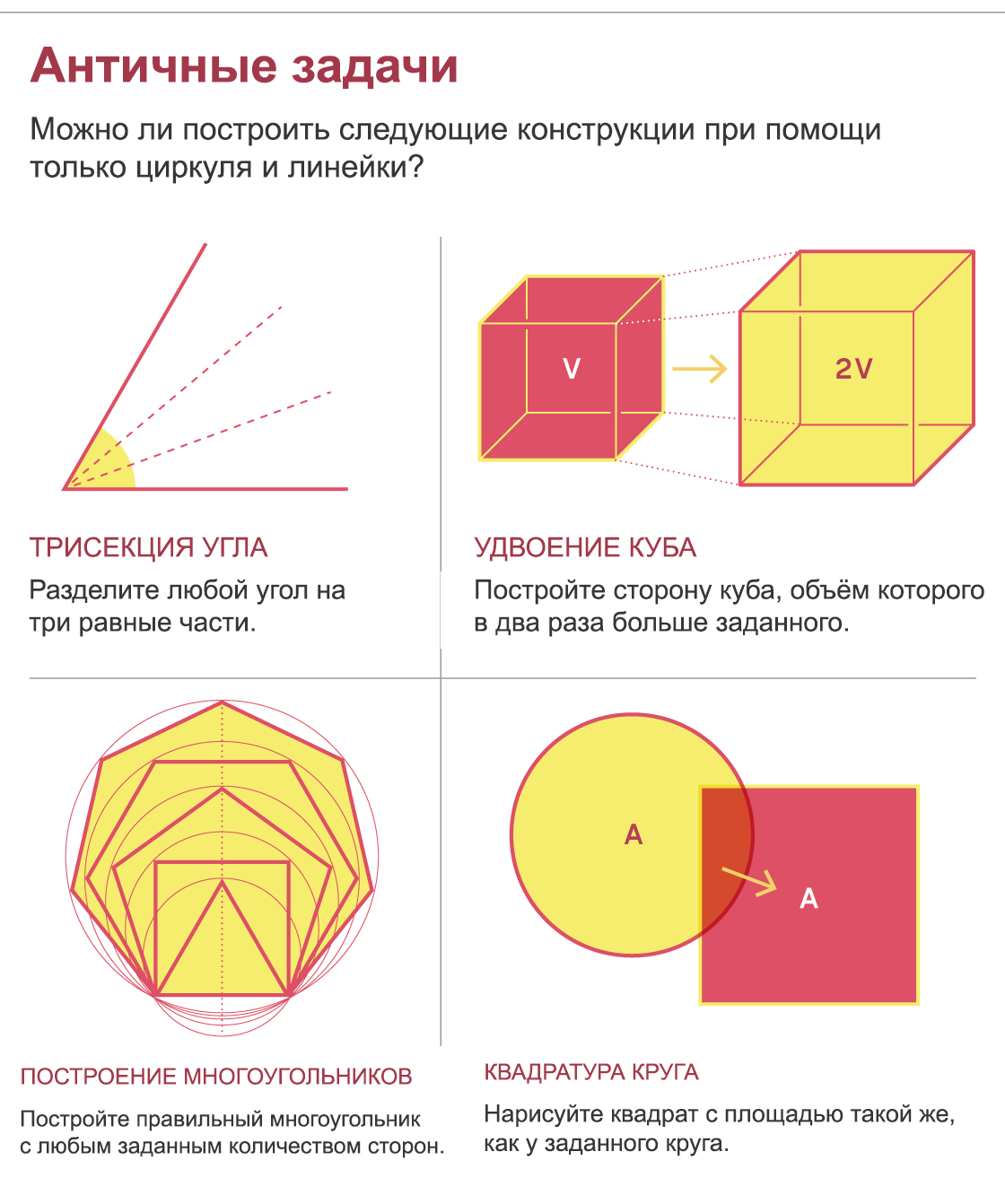
Bien que ces problèmes soient de nature géométrique, la preuve qu'ils ne peuvent pas être résolus ne l'est pas. De nouvelles mathématiques étaient nécessaires pour démontrer l'impossibilité de les résoudre.
Au 17ème siècle, René Descartes a fait une découverte fondamentale: si l'on se limite aux seuls compas et à une règle, on ne peut dessiner des segments d'aucune longueur. Si nous commençons par une ligne de longueur 1, nous ne pouvons construire que des lignes dont la longueur peut être exprimée en utilisant des entiers, l'addition, la soustraction, la multiplication, la division et la racine carrée (comme le nombre d'or).
Par conséquent, l'une des stratégies pour trouver une preuve de l'impossibilité de résoudre un problème géométrique - c'est-à-dire qu'un certain objet ne peut pas être construit - sera de montrer que la longueur d'un certain segment de la figure finale ne peut pas être exprimée de cette manière. Mais pour le montrer rigoureusement, l'algèbre émergente alors était nécessaire.
Deux siècles plus tard, le compatriote de Descartes, Pierre Laurent Vanzel , a utilisé des polynômes (sommes de coefficients et de variables élevées à une puissance) et leurs racines (variables qui rendent le polynôme égal à zéro) pour attaquer ces problèmes classiques. Par exemple, dans le problème du doublement d'un cube, le côté d'un cube avec un volume deux fois celui d'un cube unité doit être égal à... C'est la racine du polynôme x 3 -2 car...
En 1837, Wanzel a prouvé que pour qu'un segment soit construit à l'aide d'une boussole et d'une règle, sa longueur doit être la racine d'un polynôme qui ne peut pas être factorisé, et dont la puissance (la plus haute puissance de la variable) est une puissance de deux. Par exemple, le nombre d'or est la racine du polynôme du deuxième degré x 2 - x - 1. Mais x 3 -2 est un polynôme du troisième degré, doncvous ne pouvez pas construire. Wanzel a donc conclu que doubler le cube était impossible.
De la même manière, il a prouvé qu'il est impossible d'utiliser des outils classiques pour trisecter n'importe quel angle ou construire certains polygones réguliers - par exemple, un polygone à sept côtés. Fait intéressant, les trois preuves d'impossibilités ont été publiées sur la même page. Tout comme Isaac Newton et Albert Einstein avaient leur annus mirabilis (années de miracles), cette situation peut être appelée pagina mirabilis - une page de miracles.
Prouver l'impossibilité du problème restant, quadriller le cercle, exigeait quelque chose de nouveau. En 1882, Ferdinand von Lindemannprouvé le point clé - que le nombre π ne peut être construit - en prouvant sa transcendance, c'est-à-dire qu'il n'est pas la racine d'un polynôme.
Ces problèmes classiques peuvent être attribués à une mauvaise réputation et considérés comme des sirènes qui ont incité les mathématiciens à s'écraser sur les rochers acérés de l'impossibilité. Mais je les considère comme des muses qui ont inspiré des générations de penseurs créatifs.
Il en va de même pour la nouvelle tâche impossible résultant d'un acte aussi simple que la traversée d'un pont. Imaginez que vous vivez à Pittsburgh, une «ville aux ponts», comme beaucoup de mes étudiants. Tout cycliste aventureux pourrait se demander si commencer un trajet de chez lui peut traverser chacun des 22 ponts qui traversent les principales rivières de Pittsburgh exactement une fois et rentrer chez lui.
En 1735, le maire prussien fixa une tâche similaire à Leonard Euler, uniquement pour Königsberg (aujourd'hui Kaliningrad). Sept ponts de cette ville relient les trois rives du fleuve et l'île. Au début, Euler a écarté ce problème comme n'étant pas un problème mathématique: "Les solutions de ce genre ont peu à voir avec les mathématiques, et je ne comprends pas pourquoi vous attendez d'un mathématicien qu'il vous les donne et pas à quelqu'un d'autre."
Cependant, bientôt Euler a prouvé l'impossibilité de résoudre ce problème, et dans le processus a créé un nouveau domaine des mathématiques, qu'il a appelé la géométrie des arrangements - ce que nous appelons aujourd'hui la topologie. Il s'est rendu compte que les détails spécifiques - l'emplacement exact des ponts, la forme des parcelles de terrain, etc. - n'étaient pas importants. Seules leurs relations étaient importantes. Plus tard, les mathématiciens ont affiné les formulations d'Euler en utilisant ce que nous appelons aujourd'hui des graphiques. L'idée de connectivité est au cœur de l'apprentissage des médias sociaux, d'Internet, de l'épidémiologie, de la linguistique, de la planification d'itinéraire, etc.
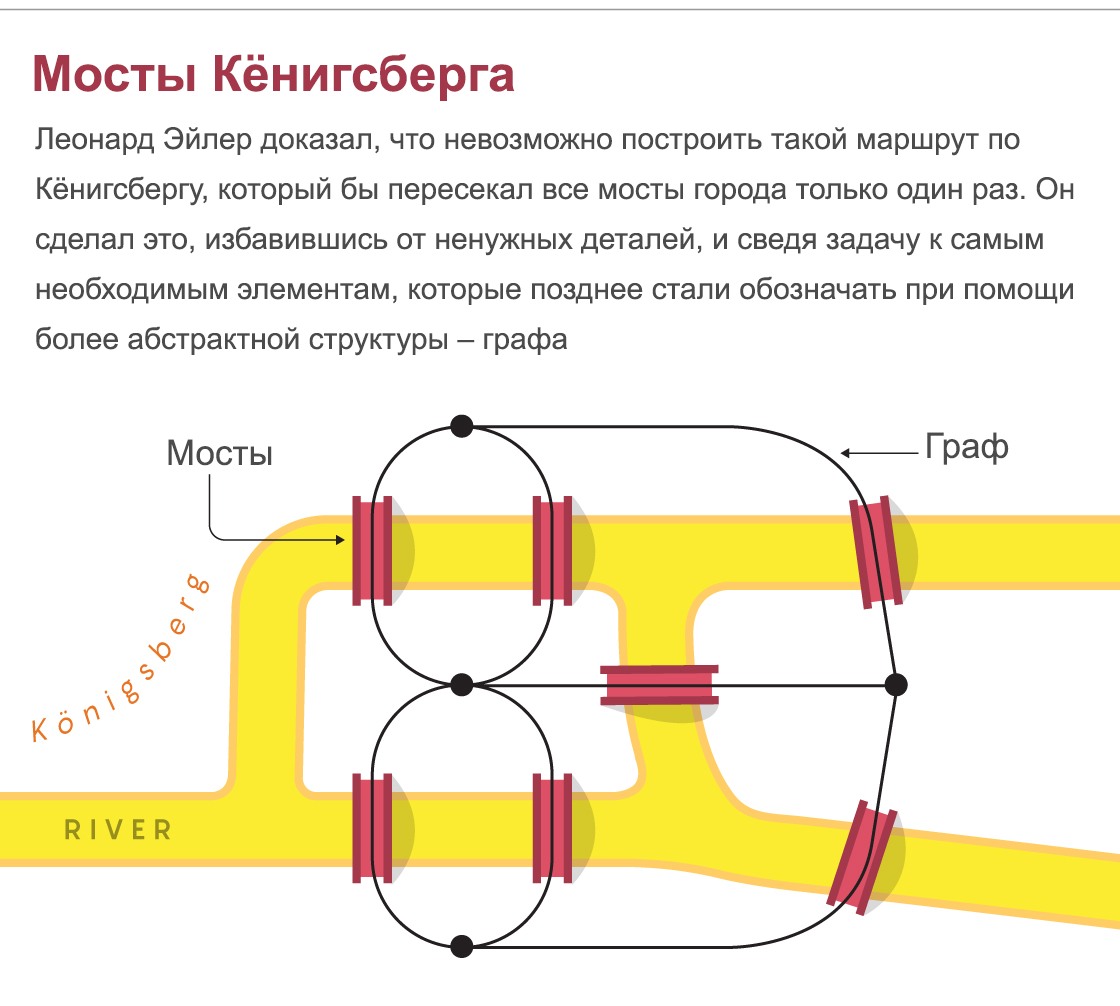
Ponts de Königsberg: Leonard Euler a prouvé qu'il est impossible de construire un itinéraire le long de Königsberg qui traverserait tous les ponts de la ville une seule fois. Il a fait cela en se débarrassant des détails inutiles et en réduisant la tâche aux éléments les plus nécessaires, qui ont ensuite commencé à être désignés en utilisant une structure plus abstraite - le graphe.
La preuve d'Euler était étonnamment simple. Il a estimé que chaque fois que nous entrons et quittons un terrain particulier, nous devons éliminer deux ponts. Par conséquent, il doit y avoir un nombre pair de ponts pour chaque parcelle de terrain. Mais comme un nombre impair de ponts menait à chaque section de Königsberg, il était impossible de construire un tel itinéraire. De même, les trois ponts menant à Gers Island sur la rivière Allegheny à Pittsburgh rendent impossible la construction de la piste cyclable souhaitée.
Comme le montre ce problème, les impossibilités ne se limitent pas aux mathématiques abstraites. Ils peuvent avoir des conséquences réelles - parfois même politiques.
Récemment, les mathématiciens se sont tournés vers le concept de gerrymendering . Aux États-Unis, après chaque recensement, les États doivent refaire les circonscriptions. Mais parfois, le parti au pouvoir réécrit ses frontières de manière ridicule pour maximiser son pouvoir politique.
De nombreux États exigent des districts «compacts» qui n'ont pas de définition mathématique stricte. En 1991, Daniel Paulsby et Robert Popper ont proposé 4πA / P 2comme moyen de mesurer la compacité de la zone A et du périmètre P. Ces valeurs vont de 1 pour une paroisse ronde à presque zéro pour les comtés déformés avec un long périmètre.
Dans l'intervalle, Nicholas Stephanopoulos et Eric McGee ont introduit «l'écart de performance» en 2014 comme une mesure de l'intégrité politique d'un plan de changement de district. Deux stratégies différentes de gerrymandering sont soit que l'opposition ait moins de 50% des voix, soit environ 100%. Chacune de ces tactiques fait perdre des voix à l'opposition en perdant les bons candidats ou en gaspillant des voix pour ceux qui ne le font pas. L'écart d'efficacité décrit le nombre relatif de votes perdus.
Ces deux mesures sont utiles pour reconnaître le gerrymandering. Mais en 2018 Boris Alekseev et Dustin Mixona prouvé que «parfois de petits écarts d'efficacité peuvent être atteints avec des comtés aux formes étranges». Autrement dit, il est mathématiquement impossible de toujours attirer les comtés pour satisfaire à la fois les exigences de Paulsby-Popper et l'intégrité de l'écart d'efficacité.
Cependant, la détection et la prévention des techniques de gerrymandering clandestines sont un domaine en croissance rapide qui attire de nombreux efforts de recherche talentueux. Comme pour les problèmes de l'Antiquité ou le problème des ponts de Königsberg, je suis sûr que le problème du gerrymendering inspirera la créativité et contribuera au développement des mathématiques.