SamsPcbCalc Partie 2: Quelle quantité de chaleur le PCB peut-il dissiper?

Avec l'amélioration de la base de l'élément, de moins en moins d'énergie se transforme en chaleur: la résistance des transistors à l'état ouvert diminue, les fréquences des convertisseurs de tension à impulsions augmentent. Mais le problème de l'évacuation de la chaleur dans le paradigme actuel des semi-conducteurs ne peut être évité, la même augmentation de productivité avec une augmentation du degré d'intégration conduit déjà à la limite de la densité de dégagement de chaleur. Pour les microcircuits dont la puissance calorifique est supérieure à 1 W, le problème thermique n'est pas moins important que le problème électrique. Dois-je dissiper la chaleur dans le boîtier? Ou utiliser un dissipateur thermique pour la puce? Pour répondre à ces questions, il n'est pas toujours nécessaire de simuler le problème thermique à l'aide d'un FEM. Dans cet article, nous considérons un modèle suffisamment flexible qui vous permet d'obtenir rapidement une estimation préliminaire de la résistance thermique carte-environnement avec une bonne précision.





L'importance du problème thermique peut être vue dans une règle empirique simplifiée qui dit que chaque augmentation de température de 10 ^{sur le} C réduit le temps de défaillance de 2 fois. Autrement dit, si à 55 ^sur une puce durera 10 ans, à 65 ^environ Avec seulement 5 arguments suffisants pour améliorer quelque peu la dissipation thermique de la puce, sinon pour jouer dans l'obsolescence prévue. Cette règle est loin d'être la vérité ultime, mais elle est qualitativement correcte (vous pouvez en savoir plus, par exemple, ici ).



L'organisation d'un dissipateur de chaleur est presque toujours un processus supplémentaire qui complique le routage et doit donc être planifié à l'avance. Pour ce faire, vous devez savoir si la carte de circuit imprimé elle-même peut gérer le dissipateur thermique. Les fabricants de _puces indiquent la résistance thermique cristalline R _{θJA dans la documentation} . Il semblerait:





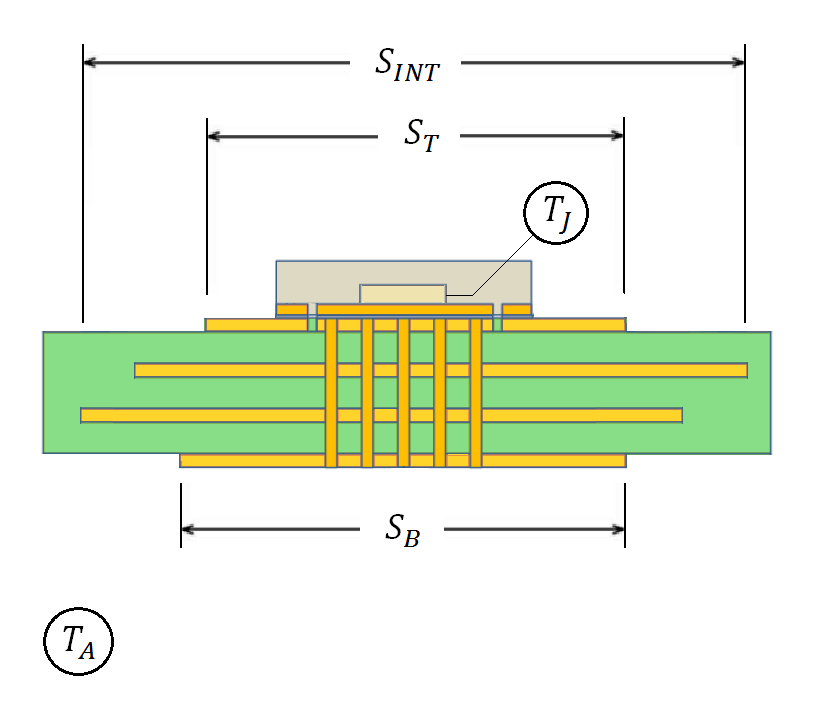
et l'estimation est prête. Mais c'est impoli, très impoli. La résistance thermique dépend fortement du PCB. Et ce qui est indiqué a été obtenu lors d'une expérience sur une carte de circuit imprimé normalisée (par exemple, comme dans la figure 1), qui, très probablement, sera très différente de ce que vous obtenez. Disons simplement que vous pouvez obtenir un bien meilleur dissipateur de chaleur avec un encombrement réduit.





Il convient de prêter attention à la résistance thermique matrice à carte R _θJB ou R _{θJC (en bas)} . C'est quelque chose qui ne dépend pas du développeur et est déterminé par le corps et sa conception interne. Mais ici, le plus souvent, le choix d'un boîtier est déterminé par la puissance de perte de chaleur, et la chute de température principale se fera sur la carte. Nous réécrivons donc la formule ci-dessus pour le cas de la dissipation thermique à travers une carte comme suit:





où R _θBA est la résistance thermique de la carte de circuit imprimé avec les paramètres donnés. Vous pouvez calculer cette résistance sur la base d'un beau modèle, qui est proposé dans lequel vous pouvez extraire un merveilleux article d'ON Semiconductor. L'article, en fait, n'est pas une instruction étape par étape, c'est une sorte d'esquisse du modèle. J'ai dû le lire 10 fois pour proposer un modèle modifié, que j'ai finalement implémenté dans une calculatrice sur la plate- forme SamsPcbLab . Les calculs sont basés sur un modèle mathématique clair (décrit ici dans cepublications du même ON Semiconductor) du problème thermique d'un anneau homogène à travers la surface interne duquel un flux thermique est chassé. La dissipation thermique est due à la convection, c'est-à-dire qu'il ne s'agit pas de vide (il faut conduire la chaleur vers le boîtier). Le diagramme du problème est présenté à la figure 2, et l'équation différentielle et la partie de sa solution qui nous intéresse sont les suivantes:







Tout avec cette équation va bien (sauf pour les fonctions de Bessel modifiées), et il peut être résolu pour une surface avec convection (en supprimant le "2" à la racine), mais seules les planches sont le plus souvent sans symétrie radiale et non homogènes, mais la chaleur est également fournie de manière inégale le long de l'intérieur rayon. Par conséquent, vous devez vous adapter. Les deux premières questions sont résolues en divisant en zones annulaires aux propriétés homogènes de même surface. Pour résoudre ce dernier, vous devez construire un modèle approximatif du circuit de résistance thermique. La figure 3 montre ce qui a été suggéré dans l'article original. Il est proposé de battre la carte en trois zones: la zone sous le microcircuit, la zone avec des polygones sur la couche externe et la zone avec uniquement des polygones sur les couches internes. Seuls les conducteurs directement connectés au microcircuit sont pris en compte (conditionnellement, «sonnerie»).



Il est proposé de faire la moyenne des polygones supérieur et inférieur et de prendre la surface de métallisation moyenne. Je ne suis pas vraiment d'accord avec cela, car l'effet sur la dissipation thermique de ces couches est évidemment différent, en plus elles peuvent différer considérablement en surface (la plus basse sera souvent plus grande en surface). Par conséquent, j'ai divisé la planche en moitiés supérieure et inférieure et j'ai fait le calcul pour chaque partie séparément.



L'article contient de nombreux graphiques avec l'influence de divers paramètres, il est utile de les regarder. J'ai calibré mon approche pour diviser la carte sur ces graphiques (Figure 4) - ils sont respectivement pour les packages QFN5X5, QFN6X6 et QFN3X3. Lorsque la carte est très grande, le graphe "tombe" sur la limite associée à la résistance thermique des vias, mais leurs paramètres ne sont pas précisés. J'ai pris un diamètre de 450 microns, une épaisseur de paroi de 20 microns, sans remplissage.









On peut voir que les modèles sont corrélés, mais je n'ai pas essayé de réaliser une coïncidence à 100%, car toutes les données d'entrée sont toujours manquantes. De plus, il y a un moment étrange avec les vias (figure 5), leur absence n'affecte pratiquement pas la résistance thermique, ce qui n'est pas très intuitif.





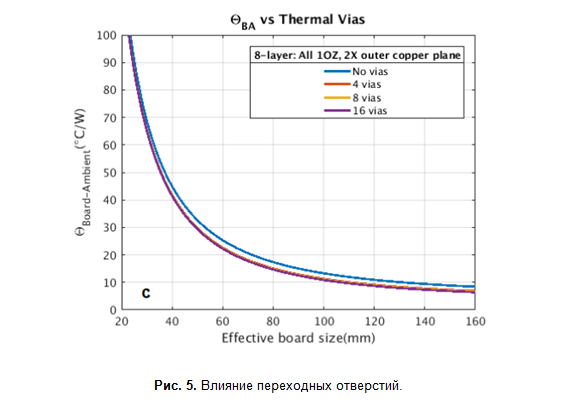
Même dans le graphique inférieur de la figure 4, vous pouvez voir deux lignes de données, où j'ai compté le modèle à deux zones par deux méthodes: en utilisant la multiplication matricielle, comme décrit dans l'article AND8222 / D, et en utilisant un modèle, comme sur la figure 3, seule la zone sous le microcircuit est écartée (il ne contribue pas à la résistance). On voit que le graphe de l'article va à peu près à la même asymptote, comme si l'influence des vias était absente. Cela pour moi est devenu un autre facteur indiquant que quelque chose ne va pas dans leur modèle, en tenant compte de l'influence des vias (ou je ne comprends pas quelque chose).



La calculatrice s'est avérée utile au moins en ce sens qu'elle permettait de passer des idées qualitatives sur l'influence de divers paramètres à des estimations quantitatives. On peut conclure que la résistance thermique de la carte peut être poussée dans la région de 10 ^oC / W même avec convection naturelle. Pour la dissipation, 2-3 W seront suffisants. Une autre remarque utile est que seul le métal directement connecté au microcircuit joue un rôle important dans le dissipateur thermique. Bien que, bien entendu, plus la fraction volumique de cuivre dans la carte est grande, plus la conductivité thermique effective sera élevée. Sur la base de ce calculateur, vous pouvez augmenter la présence d'un dissipateur thermique sur un microcircuit et d'un dissipateur thermique au boîtier, je vais également le faire. S'il y a quelque chose d'intéressant, je le partagerai dans les prochaines publications.