Normalisation intelligente des données

Cet article est apparu pour plusieurs raisons.

Premièrement, dans l'écrasante majorité des livres, des ressources Internet et des leçons sur la science des données, les nuances, les défauts des différents types de normalisation des données et leurs raisons ne sont pas du tout pris en compte, ou ne sont mentionnés qu'en passant et sans en révéler l'essence.

Deuxièmement, il y a une utilisation "aveugle", par exemple, de la normalisation pour les ensembles avec un grand nombre de fonctionnalités - "pour que ce soit la même chose pour tout le monde". Surtout pour les débutants (lui-même était le même). À première vue, ça va. Mais après un examen plus approfondi, il peut s'avérer que certains signes ont été inconsciemment placés dans une position privilégiée et ont commencé à influencer le résultat beaucoup plus fortement qu'ils ne le devraient.

Et, troisièmement, j'ai toujours voulu obtenir une méthode universelle qui prend en compte les problèmes.

La répétition est la mère de l'apprentissage

La normalisation est la conversion de données en certaines unités sans dimension. Parfois - dans une plage donnée, par exemple, [0..1] ou [-1..1]. Parfois - avec une propriété donnée, comme, par exemple, un écart type de 1.

L'objectif principal de la normalisation est de rassembler différentes données dans une grande variété d'unités et de plages de valeurs dans un seul formulaire qui vous permettra de les comparer les unes aux autres ou de les utiliser pour calculer la similitude des objets. En pratique, cela est nécessaire, par exemple, pour le clustering et dans certains algorithmes d'apprentissage automatique.

Analytiquement, toute normalisation est réduite à la formule

$$

$$X = (Xi - X)/X$$

Où $$$Xi$ - valeur actuelle,

$$$X$ - la valeur des valeurs de décalage,

$$$X$ - la taille de l'intervalle à convertir en "un"

En fait, tout se résume au fait que l'ensemble de valeurs d'origine est d'abord décalé puis mis à l'échelle.

Exemples:

Minimax (MinMax) . Le but est de convertir l'ensemble d'origine dans la plage [0..1]. Pour lui:

$$$X$= $$$X$, .

$$$X$ = $$$X$ — $$$X$, .. “” .

. — 0 1.

$$$X$= $$$X$, .

$$$X$ — .

, .

, , “” . .

, - . , . , , . , . , — . , , , , *

* — , , ( ), , .

, — .

1 —

— .. , , 0 “” .

? « » . .

№ 1 — , .

, “ ” , , — , . ( ). ( ) .

, , .

:

. “” .

, , , . .

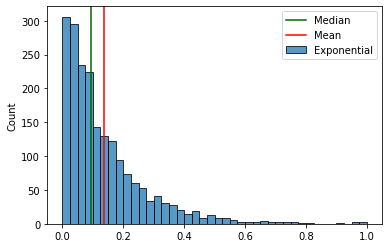
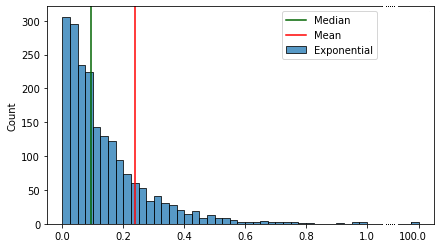
2 —

. .

. , , [-1..1], . [-1..1], — [-1..100], , . .

. . , “”.

( ):

( ) , .

, () “”, .

— ( ). , “” .

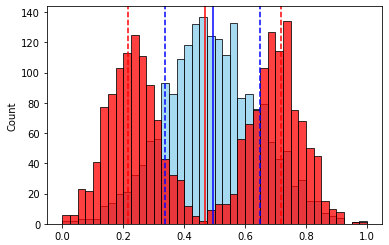
75- 25- — . .. , “” 50% . “” / .

— “”, “” .

№ 2 — “” .

— .

( ).

- “” . , , “”.

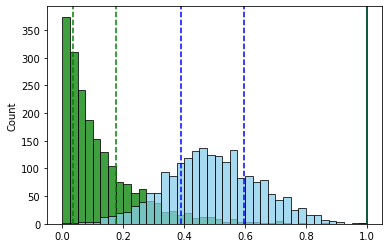
. .. . — 1.

, , , № 3 — . ( ) .

, , . 2-

, , . .

, “-”. — .

— , . , . , , , , ? .

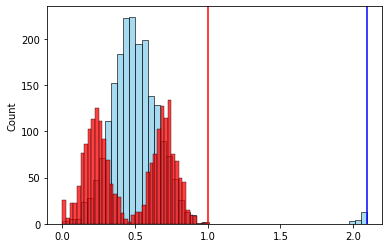
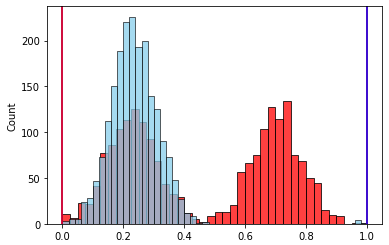
, . , “” , 1,5 (IQR) .*

* — ( .) 1,5 3 — .

.

— - , .

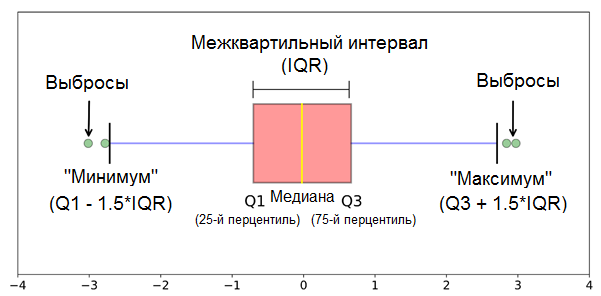
. (, , ) “” — 7%. (3 * IQR) — . . .. .

, . “ ” (1,5 * IQR) , . , - “” .

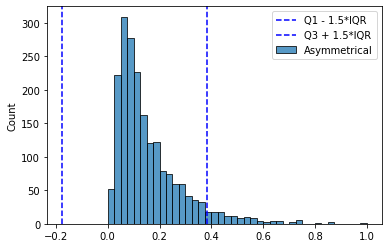
(Mia Hubert and Ellen Vandervieren) 2007 . “An Adjusted Boxplot for Skewed Distributions”.

“ ” , 1,5 * IQR.

“ ” medcouple (MC), :

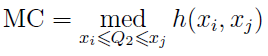
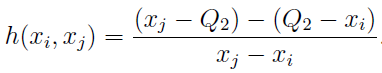
“ ” , , , 1,5 * IQR — 0,7%

:

$$$MC >= 0$:

$$$MC < 0$:

. .

, , :

1. , , .
2. .
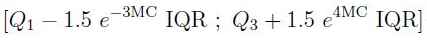
3. () — , , [0..1]

… — Mia Hubert Ellen Vandervieren

. .

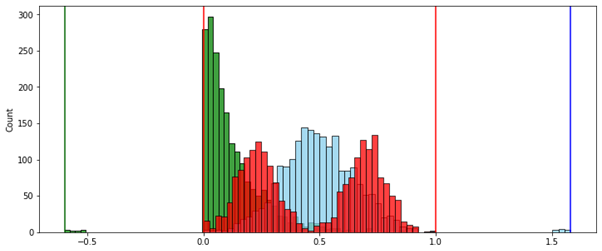
, ( ) (MinMax — ).

№ 1 — . . , “” .

:

( ):

:

, — , , .

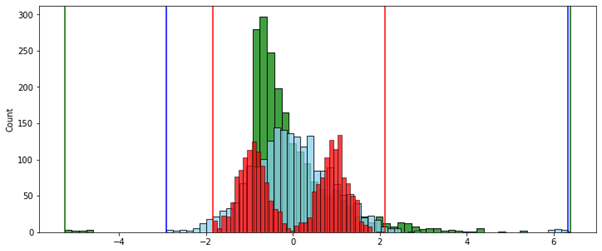
№ 2 — . [0..1]. , , .

MinMax ( ):

:

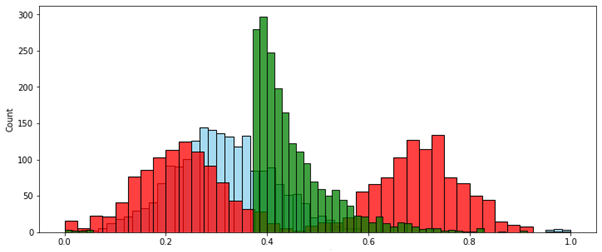
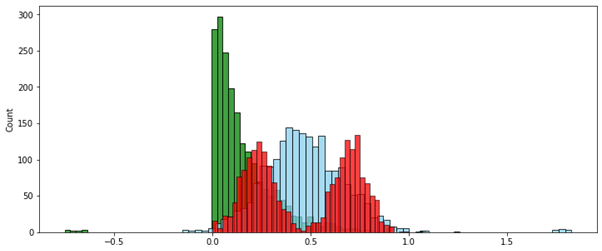
. -, , — .. 0 1.

, “” [0..1], , — , , , . .

* * *

Enfin, pour avoir la possibilité de ressentir cette méthode avec vos mains, vous pouvez essayer ma classe de démonstration AdjustedScaler à partir d'ici .

Il n'est pas optimisé pour travailler avec une très grande quantité de données et ne fonctionne qu'avec des pandas DataFrame, mais pour un essai, une expérimentation, ou même un blanc pour quelque chose de plus sérieux, il convient tout à fait. Essayez-le.