
Bonjour à tous, aujourd'hui nous allons traiter de l'algorithme de compression JPEG. Beaucoup de gens ne savent pas que JPEG n'est pas tant un format qu'un algorithme. La plupart des images JPEG que vous voyez sont au format JFIF (JPEG File Interchange Format), dans lequel l'algorithme de compression JPEG est appliqué. À la fin de l'article, vous aurez une bien meilleure compréhension de la façon dont cet algorithme compresse les données et comment écrire du code de décompression en Python. Nous ne considérerons pas toutes les nuances du format JPEG (par exemple, le balayage progressif), mais ne parlerons que des capacités de base du format pendant que nous écrivons notre propre décodeur.
introduction
Pourquoi écrire un autre article sur JPEG alors que des centaines d'articles ont déjà été écrits à ce sujet? Habituellement, dans de tels articles, les auteurs ne parlent que du format. Vous n'écrivez pas de code de déballage et de décodage. Et si vous écrivez quelque chose, ce sera en C / C ++, et ce code ne sera pas disponible pour un large éventail de personnes. Je veux briser cette tradition et vous montrer avec Python 3 comment fonctionne un décodeur JPEG de base. Il sera basé sur ce code développé par le MIT, mais je le changerai beaucoup pour des raisons de lisibilité et de clarté. Vous pouvez trouver le code modifié pour cet article dans mon référentiel .
Différentes parties de JPEG
Commençons par une photo réalisée par Ange Albertini . Il répertorie toutes les parties d'un simple fichier JPEG. Nous analyserons chaque segment et au fur et à mesure que vous lirez l'article, vous reviendrez sur cette illustration plus d'une fois.
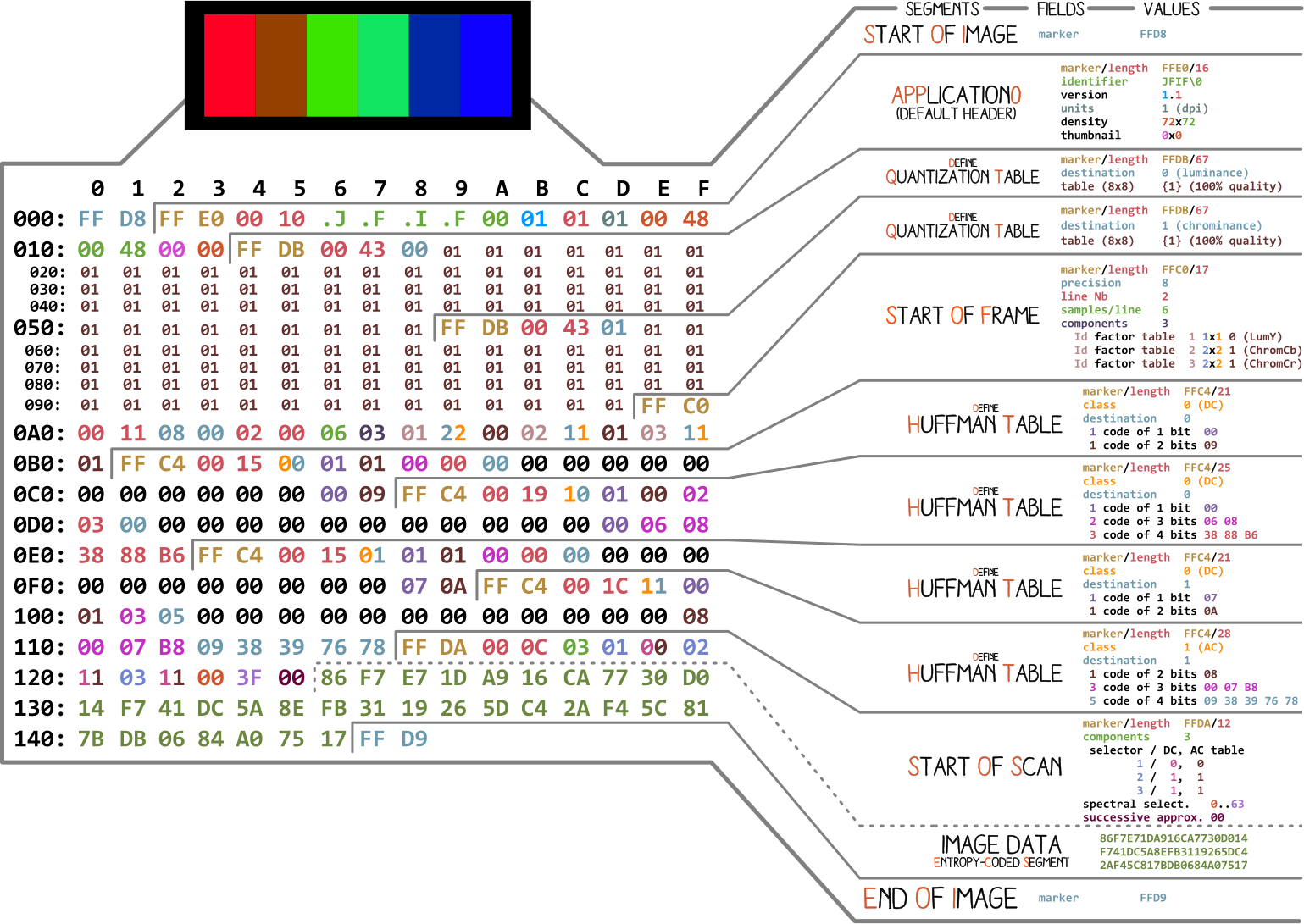
Presque tous les fichiers binaires contiennent plusieurs marqueurs (ou en-têtes). Vous pouvez les considérer comme une sorte de signets. Ils sont essentiels pour travailler avec le fichier et sont utilisés par des programmes tels que file (sur Mac et Linux) afin que nous puissions trouver les détails du fichier. Les marqueurs indiquent exactement où certaines informations sont stockées dans le fichier. Le plus souvent, les marqueurs sont placés en fonction de la valeur de longueur (
length) d'un segment particulier.
Début et fin du fichier
Le tout premier marqueur important pour nous est
FF D8. Il définit le début de l'image. Si nous ne le trouvons pas, nous pouvons supposer que le marqueur se trouve dans un autre fichier. Le marqueur n'est pas moins important FF D9. Il dit que nous avons atteint la fin du fichier image. Après chaque marqueur, à l'exception de la plage FFD0- FFD9et FF01, vient immédiatement la valeur de la longueur du segment de ce marqueur. Et les marqueurs du début et de la fin du fichier ont toujours une longueur de deux octets.
Nous allons travailler avec cette image:

Écrivons du code pour trouver les marqueurs de début et de fin.
from struct import unpack
marker_mapping = {
0xffd8: "Start of Image",
0xffe0: "Application Default Header",
0xffdb: "Quantization Table",
0xffc0: "Start of Frame",
0xffc4: "Define Huffman Table",
0xffda: "Start of Scan",
0xffd9: "End of Image"
}
class JPEG:
def __init__(self, image_file):
with open(image_file, 'rb') as f:
self.img_data = f.read()
def decode(self):
data = self.img_data
while(True):
marker, = unpack(">H", data[0:2])
print(marker_mapping.get(marker))
if marker == 0xffd8:
data = data[2:]
elif marker == 0xffd9:
return
elif marker == 0xffda:
data = data[-2:]
else:
lenchunk, = unpack(">H", data[2:4])
data = data[2+lenchunk:]
if len(data)==0:
break
if __name__ == "__main__":
img = JPEG('profile.jpg')
img.decode()
# OUTPUT:
# Start of Image
# Application Default Header
# Quantization Table
# Quantization Table
# Start of Frame
# Huffman Table
# Huffman Table
# Huffman Table
# Huffman Table
# Start of Scan
# End of Image
Pour décompresser les octets de l'image, nous avons utilisé struct .
>Hlui dit structde lire le type de données unsigned shortet de travailler avec eux dans l'ordre big-endian. Les données JPEG sont stockées dans le format le plus élevé au plus bas. Seules les données EXIF peuvent être au format little-endian (bien que ce ne soit généralement pas le cas). Et la taille shortest de 2, donc nous transférons unpackdeux octets de img_data. Comment savons-nous ce que c'est short? Nous savons que les marqueurs sont au format JPEG sont désignés par quatre caractères hexadécimaux: ffd8. Un de ces caractères équivaut à quatre bits (un demi-octet), donc quatre caractères équivaudront à deux octets, tout comme short.
Après la section Début de la numérisation, les données d'image numérisée suivent immédiatement, qui n'ont pas de longueur spécifique. Ils continuent jusqu'à la fin du marqueur de fichier, donc pendant que nous le «recherchons» manuellement lorsque nous trouvons le marqueur de début de balayage.
Traitons maintenant du reste des données d'image. Pour ce faire, nous étudions d'abord la théorie, puis passons à la programmation.
Encodage JPEG
Tout d'abord, parlons des concepts de base et des techniques de codage utilisés en JPEG. Et le codage se fera dans l'ordre inverse. D'après mon expérience, le décodage sera difficile à comprendre sans lui.
L'illustration ci-dessous n'est pas encore claire pour vous, mais je vais vous donner des conseils à mesure que vous apprenez le processus d'encodage et de décodage. Voici les étapes pour l'encodage JPEG ( source ):
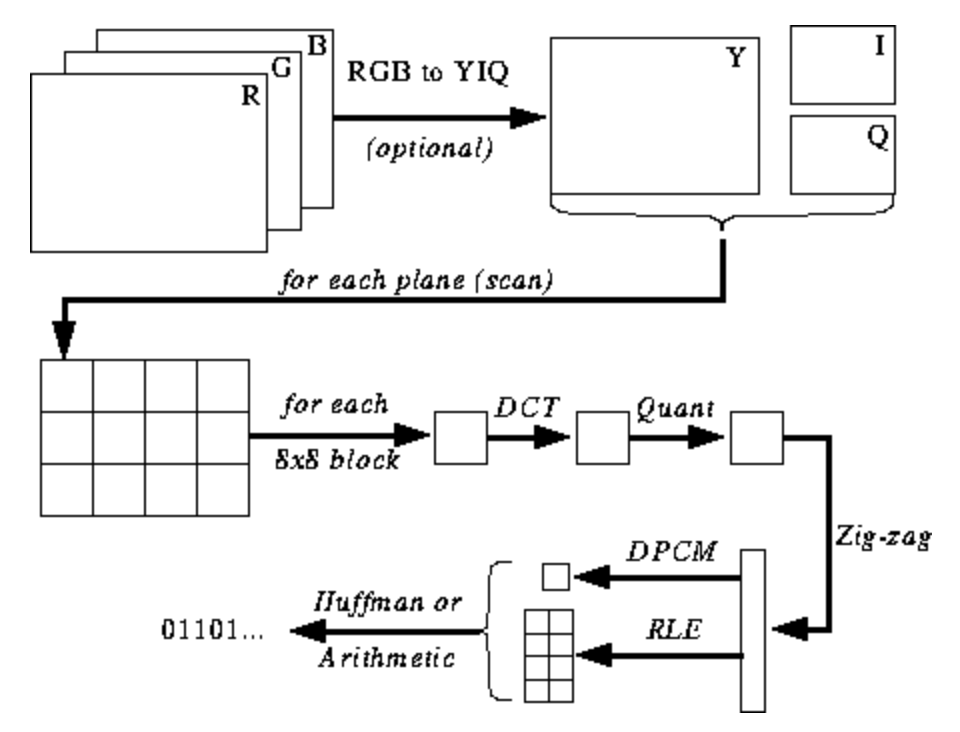
Espace colorimétrique JPEG
Selon la spécification JPEG ( ISO / IEC 10918-6: 2013 (E) Section 6.1):
- Les images codées avec un seul composant sont traitées comme des données en niveaux de gris, où 0 est noir et 255 est blanc.
- Les images encodées avec trois composants sont considérées comme des données RVB encodées dans l'espace YCbCr. Si l'image contient le segment de marqueur APP14 décrit dans la section 6.5.3, alors le codage couleur est considéré RVB ou YCbCr selon les informations du segment de marqueur APP14. La relation entre RVB et YCbCr est définie conformément à l'UIT-T T.871 | ISO / CEI 10918-5.
- , , CMYK-, (0,0,0,0) . APP14, 6.5.3, CMYK YCCK APP14. CMYK YCCK 7.
La plupart des implémentations de l'algorithme JPEG utilisent la luminance et la chrominance (codage YUV) au lieu de RVB. Ceci est très utile car l'œil humain est très pauvre pour distinguer les changements de luminosité à haute fréquence dans de petites zones, vous pouvez donc réduire la fréquence et la personne ne remarquera pas la différence. Qu'est ce que ça fait? Image hautement compressée avec une dégradation de qualité presque imperceptible.
Comme en RVB, chaque pixel est encodé avec trois octets de couleurs (rouge, vert et bleu), donc en YUV, trois octets sont utilisés, mais leur signification est différente. Le composant Y définit la luminosité de la couleur (luminance ou luma). U et V définissent la couleur (chroma): U est responsable de la partie bleue et V de la partie rouge.
Ce format a été développé à une époque où la télévision n'était pas encore si répandue et les ingénieurs voulaient utiliser le même format d'encodage d'image pour la télévision en couleur et en noir et blanc. Cliquez ici pour en savoir plus .
Transformée discrète en cosinus et quantification
JPEG convertit l'image en blocs 8x8 de pixels (appelés MCU, unité de codage minimum), modifie la plage de valeurs de pixel de sorte que le centre soit 0, puis applique une transformation en cosinus discrète à chaque bloc et compresse le résultat à l'aide de la quantification. Voyons ce que tout cela signifie.
La transformée en cosinus discrète (DCT) est une méthode de transformation de données discrètes en combinaisons d'ondes cosinus. Convertir une image en un ensemble de cosinus ressemble à un exercice futile à première vue, mais vous en comprendrez la raison lorsque vous en saurez plus sur les étapes suivantes. DCT prend un bloc de 8x8 pixels et nous indique comment reproduire ce bloc en utilisant une matrice de fonctions cosinus 8x8. Plus de détails ici .
La matrice ressemble à ceci:

Nous appliquons DCT séparément à chaque composant de pixel. En conséquence, nous obtenons une matrice 8x8 de coefficients, qui montre la contribution de chacune (des 64) fonctions cosinus dans la matrice d'entrée 8x8. Dans la matrice des coefficients DCT, les plus grandes valeurs se trouvent généralement dans le coin supérieur gauche et les plus petites dans le coin inférieur droit. Le coin supérieur gauche est la fonction cosinus de fréquence la plus basse et le coin inférieur droit est le plus élevé.
Cela signifie que dans la plupart des images, il y a une énorme quantité d'informations à basse fréquence et une petite proportion d'informations à haute fréquence. Si les composantes en bas à droite de chaque matrice DCT reçoivent la valeur 0, l'image résultante nous semblera la même, car une personne ne distingue pas mal les changements à haute fréquence. C'est ce que nous ferons à l'étape suivante.
J'ai trouvé une super vidéo sur ce sujet. Regardez si vous ne comprenez pas la signification de la PrEP:
Nous savons tous que JPEG est un algorithme de compression avec perte. Mais jusqu'à présent, nous n'avons rien perdu. Nous n'avons que des blocs de composantes YUV 8x8 convertis en blocs de fonctions cosinus 8x8 sans perte d'information. L'étape de perte de données est la quantification.
La quantification est le processus lorsque nous prenons deux valeurs d'une certaine plage et les transformons en une valeur discrète. Dans notre cas, ce n'est qu'un nom sournois pour réduire à 0 les coefficients de fréquence les plus élevés dans la matrice DCT résultante. Lors de l'enregistrement d'une image au format JPEG, la plupart des éditeurs graphiques vous demandent quel niveau de compression vous souhaitez définir. C'est là que se produit la perte d'informations à haute fréquence. Vous ne pourrez plus recréer l'image d'origine à partir de l'image JPEG résultante.
Différentes matrices de quantification sont utilisées en fonction du taux de compression (fait amusant: la plupart des développeurs ont des brevets pour créer une table de quantification). Nous divisons la matrice DCT des coefficients élément par élément par la matrice de quantification, arrondissons les résultats aux entiers et obtenons la matrice quantifiée.
Regardons un exemple. Disons qu'il existe une telle matrice DCT:

Et voici la matrice de quantification habituelle:
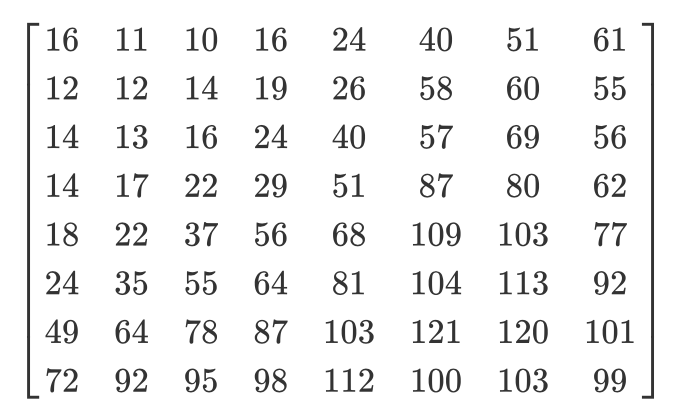
La matrice quantifiée ressemblera à ceci:

Bien que les humains ne puissent pas voir les informations à haute fréquence, si vous supprimez trop de données des blocs de 8x8 pixels, l'image aura l'air trop grossière. Dans une telle matrice quantifiée, la toute première valeur est appelée la valeur DC, et le reste est appelé la valeur AC. Si nous prenions les valeurs DC de toutes les matrices quantifiées et produisions une nouvelle image, nous obtiendrions un aperçu avec une résolution 8 fois plus petite que l'image d'origine.
Je tiens également à noter que puisque nous avons utilisé la quantification, nous devons nous assurer que les couleurs se situent dans la plage de [0,255]. S'ils s'envolent, vous devrez les amener manuellement à cette plage.
Zigzag
Après la quantification, l'algorithme JPEG utilise un balayage en zigzag pour convertir la matrice en une forme unidimensionnelle:
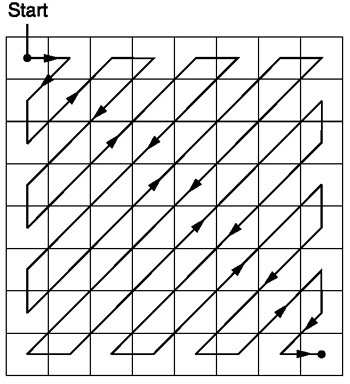
Source .
Ayons une telle matrice quantifiée:
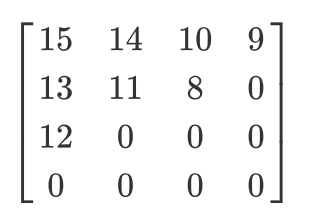
Ensuite, le résultat du scan en zigzag sera le suivant:
[15 14 13 12 11 10 9 8 0 ... 0]
Ce codage est préféré car après la quantification, la plupart des informations basse fréquence (les plus importantes) seront localisées au début de la matrice, et le balayage en zigzag stocke ces données au début de la matrice unidimensionnelle. Ceci est utile pour l'étape suivante, la compression.
Codage de longueur d'exécution et codage delta
Le codage de longueur d'exécution est utilisé pour compresser les données répétitives. Après le scan en zigzag, nous voyons qu'il y a surtout des zéros à la fin du tableau. Le codage de longueur nous permet de profiter de cet espace gaspillé et d'utiliser moins d'octets pour représenter tous ces zéros. Disons que nous avons les données suivantes:
10 10 10 10 10 10 10
Après avoir encodé les longueurs de série, nous obtenons ceci:
7 10
Nous avons compressé 7 octets en 2 octets.
Le codage delta est utilisé pour représenter un octet par rapport à l'octet qui le précède. Ce sera plus facile à expliquer avec un exemple. Ayons les données suivantes:
10 11 12 13 10 9
En utilisant le codage delta, ils peuvent être représentés comme suit:
10 1 2 3 0 -1
En JPEG, chaque valeur DC de la matrice DCT est codée en delta par rapport à la valeur DC précédente. Cela signifie qu'en changeant le tout premier coefficient DCT de l'image, vous détruirez l'image entière. Mais si vous modifiez la première valeur de la dernière matrice DCT, cela n'affectera qu'un très petit fragment de l'image.
Cette approche est utile car la première valeur DC de l'image a tendance à varier le plus, et avec le codage delta, nous rapprochons les valeurs DC restantes de 0, ce qui améliore la compression avec le codage Huffman.
Codage Huffman
C'est une méthode de compression sans perte. Un jour, Huffman s'est demandé: "Quel est le plus petit nombre de bits que je peux utiliser pour stocker du texte libre?" En conséquence, un format d'encodage a été créé. Disons que nous avons du texte:
a b c d e
En règle générale, chaque caractère occupe un octet d'espace:
a: 01100001
b: 01100010
c: 01100011
d: 01100100
e: 01100101
C'est le principe du codage ASCII binaire. Et si on change la cartographie?
# Mapping
000: 01100001
001: 01100010
010: 01100011
100: 01100100
011: 01100101
Nous avons maintenant besoin de beaucoup moins de bits pour stocker le même texte:
a: 000
b: 001
c: 010
d: 100
e: 011
C'est bien beau, mais que se passe-t-il si nous devons économiser encore plus d'espace? Par exemple, comme ceci:
# Mapping
0: 01100001
1: 01100010
00: 01100011
01: 01100100
10: 01100101
a: 0
b: 1
c: 00
d: 01
e: 10
Le codage de Huffman permet une telle correspondance de longueur variable. Les données d'entrée sont prises, les caractères les plus courants sont mis en correspondance avec une plus petite combinaison de bits et des caractères moins fréquents - avec des combinaisons plus grandes. Et puis les mappages résultants sont rassemblés dans un arbre binaire. En JPEG, nous stockons les informations DCT en utilisant le codage Huffman. Rappelez-vous que j'ai mentionné que le codage delta des valeurs DC facilite le codage Huffman? J'espère que vous comprenez maintenant pourquoi. Après l'encodage delta, nous devons faire correspondre moins de «caractères» et la taille de l'arbre est réduite.
Tom Scott a une superbe vidéo expliquant le fonctionnement de l'algorithme de Huffman. Jetez un œil avant de poursuivre votre lecture.
Un JPEG contient jusqu'à quatre tables de Huffman, qui sont stockées dans la section «Définir la table de Huffman» (commence par
0xffc4). Les coefficients DCT sont stockés dans deux tables de Huffman différentes: dans l'une les valeurs DC des tables en zigzag, dans l'autre - les valeurs AC des tables en zigzag. Cela signifie que lors du codage, nous devons combiner les valeurs DC et AC des deux matrices. Les informations DCT pour les canaux de luminance et de chromaticité sont stockées séparément, nous avons donc deux ensembles d'informations CC et deux ensembles d'informations CA, soit un total de 4 tables de Huffman.
Si l'image est en niveaux de gris, nous n'avons que deux tables de Huffman (une pour DC et une pour AC), car nous n'avons pas besoin de couleur. Comme vous l'avez peut-être compris, deux images différentes peuvent avoir des tables de Huffman très différentes, il est donc important de les stocker dans chaque JPEG.
Nous connaissons désormais le contenu principal des images JPEG. Passons au décodage.
Décodage JPEG
Le décodage peut être divisé en étapes:
- Extraction de tables de Huffman et décodage de bits.
- Extraction des coefficients DCT à l'aide de l'annulation du codage de longueur de série et delta.
- Utilisation de coefficients DCT pour combiner des ondes cosinus et reconstruire les valeurs de pixels pour chaque bloc 8x8.
- Convertissez YCbCr en RVB pour chaque pixel.
- Affiche l'image RVB résultante.
La norme JPEG prend en charge quatre formats de compression:
- Base
- Série étendue
- Progressive
- Aucune perte
Nous travaillerons avec la compression de base. Il contient une série de blocs 8x8, les uns après les autres. Dans d'autres formats, le modèle de données est légèrement différent. Pour être clair, j'ai coloré dans différents segments du contenu hexadécimal de notre image:
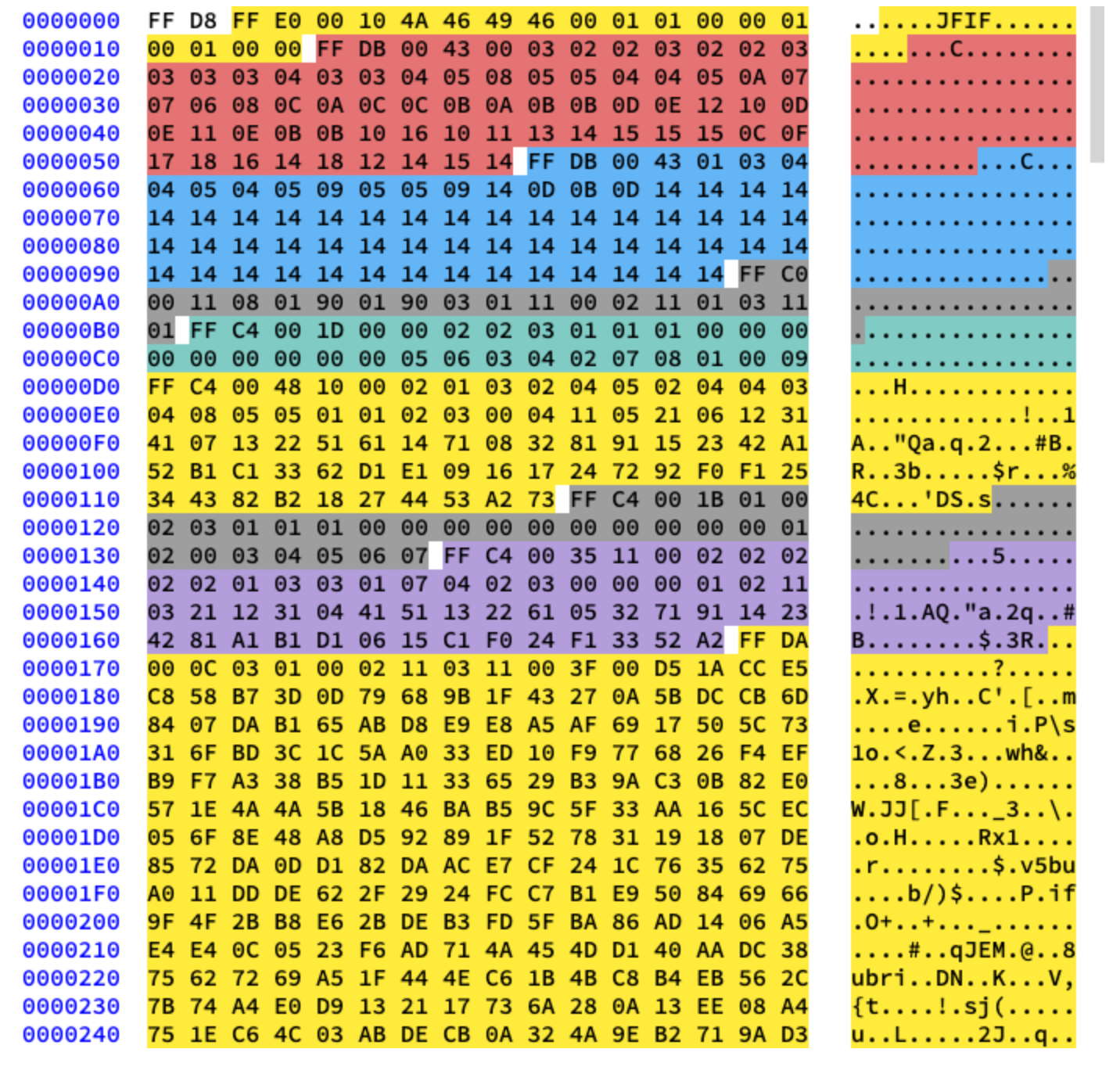
Extraction de tables Huffman
Nous savons déjà que JPEG contient quatre tables de Huffman. C'est le dernier encodage, nous allons donc commencer le décodage avec. Chaque section avec le tableau contient des informations:
| Champ | La taille | La description |
|---|---|---|
| ID du marqueur | 2 octets | 0xff et 0xc4 identifient DHT |
| Longueur | 2 octets | Longueur de la table |
| Informations sur la table de Huffman | 1 octet | bits 0 ... 3: nombre de tables (0 ... 3, sinon erreur) bit 4: type de table, 0 = table DC, 1 = tables AC bits 5 ... 7: non utilisé, doit être 0 |
| Personnages | 16 octets | Le nombre de caractères avec des codes de longueur 1 ... 16, la somme (n) de ces octets est le nombre total de codes qui doivent être <= 256 |
| Symboles | n octets | Le tableau contient des caractères par ordre croissant de longueur de code (n = nombre total de codes). |
Disons que nous avons une table de Huffman comme celle-ci ( source ):
| symbole | Code de Huffman | Longueur du code |
|---|---|---|
| une | 00 | 2 |
| b | 010 | 3 |
| c | 011 | 3 |
| ré | 100 | 3 |
| e | 101 | 3 |
| F | 110 | 3 |
| g | 1110 | 4 |
| h | 11110 | cinq |
| je | 111110 | 6 |
| j | 1111110 | 7 |
| k | 11111110 | 8 |
| l | 111111110 | neuf |
Il sera stocké dans un fichier JFIF comme celui-ci (au format binaire. J'utilise ASCII pour plus de clarté uniquement):
0 1 5 1 1 1 1 1 1 0 0 0 0 0 0 0 a b c d e f g h i j k l
0 signifie que nous n'avons pas de code Huffman de longueur 1. Un 1 signifie que nous avons un code Huffman de longueur 2, et ainsi de suite. Dans la section DHT, immédiatement après la classe et l'ID, les données sont toujours longues de 16 octets. Écrivons le code pour extraire les longueurs et les éléments de DHT.
class JPEG:
# ...
def decodeHuffman(self, data):
offset = 0
header, = unpack("B",data[offset:offset+1])
offset += 1
# Extract the 16 bytes containing length data
lengths = unpack("BBBBBBBBBBBBBBBB", data[offset:offset+16])
offset += 16
# Extract the elements after the initial 16 bytes
elements = []
for i in lengths:
elements += (unpack("B"*i, data[offset:offset+i]))
offset += i
print("Header: ",header)
print("lengths: ", lengths)
print("Elements: ", len(elements))
data = data[offset:]
def decode(self):
data = self.img_data
while(True):
# ---
else:
len_chunk, = unpack(">H", data[2:4])
len_chunk += 2
chunk = data[4:len_chunk]
if marker == 0xffc4:
self.decodeHuffman(chunk)
data = data[len_chunk:]
if len(data)==0:
break
Après avoir exécuté le code, nous obtenons ceci:
Start of Image
Application Default Header
Quantization Table
Quantization Table
Start of Frame
Huffman Table
Header: 0
lengths: (0, 2, 2, 3, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0)
Elements: 10
Huffman Table
Header: 16
lengths: (0, 2, 1, 3, 2, 4, 5, 2, 4, 4, 3, 4, 8, 5, 5, 1)
Elements: 53
Huffman Table
Header: 1
lengths: (0, 2, 3, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0)
Elements: 8
Huffman Table
Header: 17
lengths: (0, 2, 2, 2, 2, 2, 1, 3, 3, 1, 7, 4, 2, 3, 0, 0)
Elements: 34
Start of Scan
End of Image
Excellent! Nous avons des longueurs et des éléments. Vous devez maintenant créer votre propre classe de table Huffman afin de reconstruire l'arbre binaire à partir des longueurs et des éléments obtenus. Je vais juste copier le code d'ici :
class HuffmanTable:
def __init__(self):
self.root=[]
self.elements = []
def BitsFromLengths(self, root, element, pos):
if isinstance(root,list):
if pos==0:
if len(root)<2:
root.append(element)
return True
return False
for i in [0,1]:
if len(root) == i:
root.append([])
if self.BitsFromLengths(root[i], element, pos-1) == True:
return True
return False
def GetHuffmanBits(self, lengths, elements):
self.elements = elements
ii = 0
for i in range(len(lengths)):
for j in range(lengths[i]):
self.BitsFromLengths(self.root, elements[ii], i)
ii+=1
def Find(self,st):
r = self.root
while isinstance(r, list):
r=r[st.GetBit()]
return r
def GetCode(self, st):
while(True):
res = self.Find(st)
if res == 0:
return 0
elif ( res != -1):
return res
class JPEG:
# -----
def decodeHuffman(self, data):
# ----
hf = HuffmanTable()
hf.GetHuffmanBits(lengths, elements)
data = data[offset:]
GetHuffmanBitsprend les longueurs et les éléments, effectue une itération sur les éléments et les met dans une liste root. C'est un arbre binaire et contient des listes imbriquées. Vous pouvez lire sur Internet comment fonctionne l'arbre de Huffman et comment créer une telle structure de données en Python. Pour notre premier DHT (à partir de l'image au début de l'article), nous avons les données, longueurs et éléments suivants:
Hex Data: 00 02 02 03 01 01 01 00 00 00 00 00 00 00 00 00
Lengths: (0, 2, 2, 3, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0)
Elements: [5, 6, 3, 4, 2, 7, 8, 1, 0, 9]
Après l'appel, la
GetHuffmanBitsliste rootcontiendra les données suivantes:
[[5, 6], [[3, 4], [[2, 7], [8, [1, [0, [9]]]]]]]
HuffmanTablecontient également une méthode GetCodequi parcourt l'arborescence et utilise une table de Huffman pour renvoyer les bits décodés. La méthode reçoit un train de bits en entrée - juste une représentation binaire des données. Par exemple, le flux binaire pour abcsera 011000010110001001100011. Tout d'abord, nous convertissons chaque caractère en son code ASCII, que nous convertissons en binaire. Créons une classe pour nous aider à convertir une chaîne en bits, puis comptons les bits un par un:
class Stream:
def __init__(self, data):
self.data= data
self.pos = 0
def GetBit(self):
b = self.data[self.pos >> 3]
s = 7-(self.pos & 0x7)
self.pos+=1
return (b >> s) & 1
def GetBitN(self, l):
val = 0
for i in range(l):
val = val*2 + self.GetBit()
return val
Lors de l'initialisation, nous donnons à la classe des données binaires, puis les lisons en utilisant
GetBitet GetBitN.
Décoder la table de quantification
La section Définir la table de quantification contient les données suivantes:
| Champ | La taille | La description |
|---|---|---|
| ID du marqueur | 2 octets | 0xff et 0xdb identifient la section DQT |
| Longueur | 2 octets | Longueur de la table de quantification |
| Informations de quantification | 1 octet | bits 0 ... 3: nombre de tables de quantification (0 ... 3, sinon erreur) bits 4 ... 7: précision de la table de quantification, 0 = 8 bits, sinon 16 bits |
| Octets | n octets | Valeurs de la table de quantification, n = 64 * (précision + 1) |
Selon la norme JPEG, l'image JPEG par défaut a deux tables de quantification: pour la luminance et la chrominance. Ils commencent par un marqueur
0xffdb. Le résultat de notre code contient déjà deux de ces marqueurs. Ajoutons la possibilité de décoder les tables de quantification:
def GetArray(type,l, length):
s = ""
for i in range(length):
s =s+type
return list(unpack(s,l[:length]))
class JPEG:
# ------
def __init__(self, image_file):
self.huffman_tables = {}
self.quant = {}
with open(image_file, 'rb') as f:
self.img_data = f.read()
def DefineQuantizationTables(self, data):
hdr, = unpack("B",data[0:1])
self.quant[hdr] = GetArray("B", data[1:1+64],64)
data = data[65:]
def decodeHuffman(self, data):
# ------
for i in lengths:
elements += (GetArray("B", data[off:off+i], i))
offset += i
# ------
def decode(self):
# ------
while(True):
# ----
else:
# -----
if marker == 0xffc4:
self.decodeHuffman(chunk)
elif marker == 0xffdb:
self.DefineQuantizationTables(chunk)
data = data[len_chunk:]
if len(data)==0:
break
Nous avons d'abord défini la méthode
GetArray. C'est juste une technique pratique pour décoder un nombre variable d'octets à partir de données binaires. Nous avons également remplacé une partie du code de la méthode decodeHuffmanpour profiter de la nouvelle fonction. Ensuite, la méthode a été définie DefineQuantizationTables: elle lit le titre de la section avec les tables de quantification, puis applique les données de quantification au dictionnaire, en utilisant la valeur de l'en-tête comme clé. cette valeur peut être 0 pour la luminance et 1 pour la chromaticité. Chaque section avec des tables de quantification dans JFIF contient 64 octets de données (pour une matrice de quantification 8x8).
Si nous sortons les matrices de quantification pour notre image, nous obtenons ceci:
3 2 2 3 2 2 3 3
3 3 4 3 3 4 5 8
5 5 4 4 5 10 7 7
6 8 12 10 12 12 11 10
11 11 13 14 18 16 13 14
17 14 11 11 16 22 16 17
19 20 21 21 21 12 15 23
24 22 20 24 18 20 21 20
3 2 2 3 2 2 3 3
3 2 2 3 2 2 3 3
3 3 4 3 3 4 5 8
5 5 4 4 5 10 7 7
6 8 12 10 12 12 11 10
11 11 13 14 18 16 13 14
17 14 11 11 16 22 16 17
19 20 21 21 21 12 15 23
24 22 20 24 18 20 21 20
Décodage du début de l'image
La section Début de l'image contient les informations suivantes ( source ):
| Champ | La taille | La description |
|---|---|---|
| ID du marqueur | 2 octets | 0xff 0xc0 SOF |
| 2 | 8 + *3 | |
| 1 | , 8 (12 16 ). | |
| 2 | > 0 | |
| 2 | > 0 | |
| 1 | 1 = , 3 = YcbCr YIQ | |
| 3 | 3 . (1 ) (1 = Y, 2 = Cb, 3 = Cr, 4 = I, 5 = Q), (1 ) ( 0...3 , 4...7 ), (1 ). |
Ici, on ne s'intéresse pas à tout. Nous allons extraire la largeur et la hauteur de l'image, ainsi que le nombre de tables de quantification pour chaque composant. La largeur et la hauteur seront utilisées pour commencer le décodage des numérisations réelles de l'image à partir de la section Début de la numérisation. Puisque nous travaillerons principalement avec une image YCbCr, nous pouvons supposer qu'il y aura trois composants et que leurs types seront 1, 2 et 3, respectivement. Écrivons le code pour décoder ces données:
class JPEG:
def __init__(self, image_file):
self.huffman_tables = {}
self.quant = {}
self.quantMapping = []
with open(image_file, 'rb') as f:
self.img_data = f.read()
# ----
def BaselineDCT(self, data):
hdr, self.height, self.width, components = unpack(">BHHB",data[0:6])
print("size %ix%i" % (self.width, self.height))
for i in range(components):
id, samp, QtbId = unpack("BBB",data[6+i*3:9+i*3])
self.quantMapping.append(QtbId)
def decode(self):
# ----
while(True):
# -----
elif marker == 0xffdb:
self.DefineQuantizationTables(chunk)
elif marker == 0xffc0:
self.BaselineDCT(chunk)
data = data[len_chunk:]
if len(data)==0:
break
Nous avons ajouté un attribut de liste à la classe JPEG
quantMappinget défini une méthode BaselineDCTqui décode les données requises de la section SOF et met le nombre de tables de quantification pour chaque composant dans la liste quantMapping. Nous en profiterons lorsque nous commencerons à lire la section Début de l'analyse. Voici à quoi ressemble notre image quantMapping:
Quant mapping: [0, 1, 1]
Décodage du début du scan
C'est la "viande" d'une image JPEG, elle contient les données de l'image elle-même. Nous avons atteint l'étape la plus importante. Tout ce que nous avons décodé auparavant peut être considéré comme une carte qui nous aide à décoder l'image elle-même. Cette section contient l'image elle-même (encodée). Nous lisons la section et décrypterons en utilisant les données déjà décodées.
Tous les marqueurs ont commencé par
0xff. Cette valeur peut également faire partie de l'image numérisée, mais si elle est présente dans cette section, elle sera toujours suivie de et 0x00. L'encodeur JPEG l'insère automatiquement, c'est ce qu'on appelle le bourrage d'octets. Par conséquent, le décodeur doit les supprimer 0x00. Commençons par la méthode de décodage SOS contenant une telle fonction et débarrassons-nous de celles existantes 0x00. Dans notre image dans la section avec un scan il n'y a pas0xffmais c'est toujours un ajout utile.
def RemoveFF00(data):
datapro = []
i = 0
while(True):
b,bnext = unpack("BB",data[i:i+2])
if (b == 0xff):
if (bnext != 0):
break
datapro.append(data[i])
i+=2
else:
datapro.append(data[i])
i+=1
return datapro,i
class JPEG:
# ----
def StartOfScan(self, data, hdrlen):
data,lenchunk = RemoveFF00(data[hdrlen:])
return lenchunk+hdrlen
def decode(self):
data = self.img_data
while(True):
marker, = unpack(">H", data[0:2])
print(marker_mapping.get(marker))
if marker == 0xffd8:
data = data[2:]
elif marker == 0xffd9:
return
else:
len_chunk, = unpack(">H", data[2:4])
len_chunk += 2
chunk = data[4:len_chunk]
if marker == 0xffc4:
self.decodeHuffman(chunk)
elif marker == 0xffdb:
self.DefineQuantizationTables(chunk)
elif marker == 0xffc0:
self.BaselineDCT(chunk)
elif marker == 0xffda:
len_chunk = self.StartOfScan(data, len_chunk)
data = data[len_chunk:]
if len(data)==0:
break
Auparavant, nous recherchions manuellement la fin du fichier lorsque nous trouvions un marqueur
0xffda, mais maintenant que nous avons un outil qui nous permet de visualiser systématiquement l'ensemble du fichier, nous allons déplacer la condition de recherche de marqueur à l'intérieur de l'opérateur else. La fonction RemoveFF00s'arrête juste quand elle trouve autre chose au lieu de 0x00après 0xff. La boucle se rompt lorsque la fonction trouve 0xffd9, nous pouvons donc rechercher la fin du fichier sans crainte de surprises. Si vous exécutez ce code, vous ne verrez rien de nouveau dans le terminal.
N'oubliez pas que JPEG divise l'image en matrices 8x8. Nous devons maintenant convertir les données d'image numérisées en un flux binaire et les traiter en blocs de 8x8. Ajoutons le code à notre classe:
class JPEG:
# -----
def StartOfScan(self, data, hdrlen):
data,lenchunk = RemoveFF00(data[hdrlen:])
st = Stream(data)
oldlumdccoeff, oldCbdccoeff, oldCrdccoeff = 0, 0, 0
for y in range(self.height//8):
for x in range(self.width//8):
matL, oldlumdccoeff = self.BuildMatrix(st,0, self.quant[self.quantMapping[0]], oldlumdccoeff)
matCr, oldCrdccoeff = self.BuildMatrix(st,1, self.quant[self.quantMapping[1]], oldCrdccoeff)
matCb, oldCbdccoeff = self.BuildMatrix(st,1, self.quant[self.quantMapping[2]], oldCbdccoeff)
DrawMatrix(x, y, matL.base, matCb.base, matCr.base )
return lenchunk +hdrlen
Commençons par convertir les données en un flux binaire. Vous souvenez-vous que le codage delta est appliqué à l'élément DC de la matrice de quantification (son premier élément) par rapport à l'élément DC précédent? Par conséquent, nous initialisons
oldlumdccoeff, oldCbdccoeffet oldCrdccoeffavec zéro valeurs, ils nous aider à garder une trace de la valeur des éléments précédents DC, et 0 est défini par défaut lorsque nous trouvons le premier élément DC.
La boucle
forpeut sembler étrange. self.height//8nous dit combien de fois nous pouvons diviser la hauteur par 8 8, et c'est la même chose avec la largeur et self.width//8.
BuildMatrixprendra une table de quantification et ajoutera des paramètres, créera une matrice de transformation en cosinus discrète inverse et nous donnera les matrices Y, Cr et Cb. Et la fonction les DrawMatrixconvertit en RVB.
Tout d'abord, créons une classe
IDCT, puis commencez à remplir la méthode BuildMatrix.
import math
class IDCT:
"""
An inverse Discrete Cosine Transformation Class
"""
def __init__(self):
self.base = [0] * 64
self.zigzag = [
[0, 1, 5, 6, 14, 15, 27, 28],
[2, 4, 7, 13, 16, 26, 29, 42],
[3, 8, 12, 17, 25, 30, 41, 43],
[9, 11, 18, 24, 31, 40, 44, 53],
[10, 19, 23, 32, 39, 45, 52, 54],
[20, 22, 33, 38, 46, 51, 55, 60],
[21, 34, 37, 47, 50, 56, 59, 61],
[35, 36, 48, 49, 57, 58, 62, 63],
]
self.idct_precision = 8
self.idct_table = [
[
(self.NormCoeff(u) * math.cos(((2.0 * x + 1.0) * u * math.pi) / 16.0))
for x in range(self.idct_precision)
]
for u in range(self.idct_precision)
]
def NormCoeff(self, n):
if n == 0:
return 1.0 / math.sqrt(2.0)
else:
return 1.0
def rearrange_using_zigzag(self):
for x in range(8):
for y in range(8):
self.zigzag[x][y] = self.base[self.zigzag[x][y]]
return self.zigzag
def perform_IDCT(self):
out = [list(range(8)) for i in range(8)]
for x in range(8):
for y in range(8):
local_sum = 0
for u in range(self.idct_precision):
for v in range(self.idct_precision):
local_sum += (
self.zigzag[v][u]
* self.idct_table[u][x]
* self.idct_table[v][y]
)
out[y][x] = local_sum // 4
self.base = out
Analysons la classe
IDCT. Lorsque nous extrayons le MCU, il sera stocké dans un attribut base. Ensuite, nous transformons la matrice MCU en annulant le balayage en zigzag à l'aide de la méthode rearrange_using_zigzag. Enfin, nous annulerons la transformation en cosinus discrète en appelant la méthode perform_IDCT.
Comme vous vous en souvenez, la table DC est fixe. Nous ne considérerons pas le fonctionnement de DCT, cela est plus lié aux mathématiques qu'à la programmation. Nous pouvons stocker cette table en tant que variable globale et demander des paires de valeurs
x,y. J'ai décidé de mettre le tableau et son calcul dans une classe IDCTpour rendre le texte lisible. Chaque élément de la matrice MCU transformée est multiplié par une valeur idc_variableet nous obtenons les valeurs Y, Cr et Cb.
Cela deviendra plus clair lorsque nous ajouterons la méthode
BuildMatrix.
Si vous modifiez la table en zigzag pour qu'elle ressemble à ceci:
[[ 0, 1, 5, 6, 14, 15, 27, 28],
[ 2, 4, 7, 13, 16, 26, 29, 42],
[ 3, 8, 12, 17, 25, 30, 41, 43],
[20, 22, 33, 38, 46, 51, 55, 60],
[21, 34, 37, 47, 50, 56, 59, 61],
[35, 36, 48, 49, 57, 58, 62, 63],
[ 9, 11, 18, 24, 31, 40, 44, 53],
[10, 19, 23, 32, 39, 45, 52, 54]]
vous obtenez ce résultat (notez les petits artefacts):

Et si vous avez le courage, vous pouvez modifier encore plus le tableau en zigzag:
[[12, 19, 26, 33, 40, 48, 41, 34,],
[27, 20, 13, 6, 7, 14, 21, 28,],
[ 0, 1, 8, 16, 9, 2, 3, 10,],
[17, 24, 32, 25, 18, 11, 4, 5,],
[35, 42, 49, 56, 57, 50, 43, 36,],
[29, 22, 15, 23, 30, 37, 44, 51,],
[58, 59, 52, 45, 38, 31, 39, 46,],
[53, 60, 61, 54, 47, 55, 62, 63]]
Ensuite, le résultat sera comme ceci:

Complétons notre méthode
BuildMatrix:
def DecodeNumber(code, bits):
l = 2**(code-1)
if bits>=l:
return bits
else:
return bits-(2*l-1)
class JPEG:
# -----
def BuildMatrix(self, st, idx, quant, olddccoeff):
i = IDCT()
code = self.huffman_tables[0 + idx].GetCode(st)
bits = st.GetBitN(code)
dccoeff = DecodeNumber(code, bits) + olddccoeff
i.base[0] = (dccoeff) * quant[0]
l = 1
while l < 64:
code = self.huffman_tables[16 + idx].GetCode(st)
if code == 0:
break
# The first part of the AC quantization table
# is the number of leading zeros
if code > 15:
l += code >> 4
code = code & 0x0F
bits = st.GetBitN(code)
if l < 64:
coeff = DecodeNumber(code, bits)
i.base[l] = coeff * quant[l]
l += 1
i.rearrange_using_zigzag()
i.perform_IDCT()
return i, dccoeff
Nous commençons par créer une classe d'inversion de transformée cosinus discrète (
IDCT()). Ensuite, nous lisons les données dans le train de bits et les décodons à l'aide d'une table de Huffman.
self.huffman_tables[0]et self.huffman_tables[1]reportez - vous aux tableaux DC pour la luminance et la chrominance, respectivement, et self.huffman_tables[16]et self.huffman_tables[17]reportez - vous aux tableaux AC pour la luminance et la chrominance, respectivement.
Après avoir décodé le train de bits, nous utilisons une fonction pour
DecodeNumber extraire le nouveau coefficient DC codé en delta et y ajouter olddccoefficientpour obtenir le coefficient DC décodé en delta .
Ensuite, nous répétons la même procédure de décodage avec les valeurs AC dans la matrice de quantification. Signification du code
0indique que nous avons atteint le marqueur de fin de bloc (EOB) et que nous devons nous arrêter. De plus, la première partie du tableau de quantification AC nous indique le nombre de zéros non significatifs que nous avons. Souvenons-nous maintenant du codage des longueurs de la série. Inversons ce processus et sautons tous ces nombreux bits. IDCTDes zéros leur sont explicitement attribués dans la classe .
Après avoir décodé les valeurs DC et AC pour le MCU, nous convertissons le MCU et inversons le balayage en zigzag en appelant
rearrange_using_zigzag. Et puis nous inversons le DCT et nous l'appliquons au MCU décodé.
La méthode
BuildMatrixretournera la matrice DCT inversée et la valeur du coefficient DC. N'oubliez pas que ce sera une matrice pour une seule unité d'encodage 8x8 minimum. Faisons cela pour tous les autres MCU de notre fichier.
Affichage d'une image à l'écran
Maintenant, faisons notre code dans la méthode
StartOfScancréer un Tkinter Canvas et dessiner chaque MCU après le décodage.
def Clamp(col):
col = 255 if col>255 else col
col = 0 if col<0 else col
return int(col)
def ColorConversion(Y, Cr, Cb):
R = Cr*(2-2*.299) + Y
B = Cb*(2-2*.114) + Y
G = (Y - .114*B - .299*R)/.587
return (Clamp(R+128),Clamp(G+128),Clamp(B+128) )
def DrawMatrix(x, y, matL, matCb, matCr):
for yy in range(8):
for xx in range(8):
c = "#%02x%02x%02x" % ColorConversion(
matL[yy][xx], matCb[yy][xx], matCr[yy][xx]
)
x1, y1 = (x * 8 + xx) * 2, (y * 8 + yy) * 2
x2, y2 = (x * 8 + (xx + 1)) * 2, (y * 8 + (yy + 1)) * 2
w.create_rectangle(x1, y1, x2, y2, fill=c, outline=c)
class JPEG:
# -----
def StartOfScan(self, data, hdrlen):
data,lenchunk = RemoveFF00(data[hdrlen:])
st = Stream(data)
oldlumdccoeff, oldCbdccoeff, oldCrdccoeff = 0, 0, 0
for y in range(self.height//8):
for x in range(self.width//8):
matL, oldlumdccoeff = self.BuildMatrix(st,0, self.quant[self.quantMapping[0]], oldlumdccoeff)
matCr, oldCrdccoeff = self.BuildMatrix(st,1, self.quant[self.quantMapping[1]], oldCrdccoeff)
matCb, oldCbdccoeff = self.BuildMatrix(st,1, self.quant[self.quantMapping[2]], oldCbdccoeff)
DrawMatrix(x, y, matL.base, matCb.base, matCr.base )
return lenchunk+hdrlen
if __name__ == "__main__":
from tkinter import *
master = Tk()
w = Canvas(master, width=1600, height=600)
w.pack()
img = JPEG('profile.jpg')
img.decode()
mainloop()
Commençons par les fonctions
ColorConversionet Clamp. ColorConversionprend les valeurs Y, Cr et Cb, les convertit en composants RVB par la formule, puis génère les valeurs RVB agrégées. Pourquoi en ajouter 128, pourriez-vous demander? Rappelez-vous, avant l'algorithme JPEG, DCT est appliqué au MCU et soustrait 128 des valeurs de couleur. Si les couleurs étaient à l'origine dans la plage [0,255], JPEG les placera dans la plage [-128, + 128]. Nous devons annuler cet effet lors du décodage, nous ajoutons donc 128 à RVB. Quant au Clampdéballage, les valeurs résultantes peuvent sortir de la plage [0,255], nous les gardons donc dans cette plage [0,255].
Dans la méthode
DrawMatrixnous parcourons chaque matrice 8x8 décodée pour Y, Cr et Cb, et convertissons chaque élément de matrice en valeurs RVB. Après transformation, nous dessinons des pixels dans Tkinter en canvasutilisant la méthode create_rectangle. Vous pouvez trouver tout le code sur GitHub . Si vous l'exécutez, mon visage apparaîtra à l'écran.
Conclusion
Qui aurait pensé que pour montrer mon visage, il faudrait écrire une explication de plus de 6 000 mots. C'est incroyable à quel point les auteurs de certains algorithmes étaient intelligents! J'espère que vous avez apprécié l'article. J'ai beaucoup appris en écrivant ce décodeur. Je ne pensais pas qu'il y avait autant de mathématiques impliquées dans l'encodage d'une simple image JPEG. La prochaine fois, vous pourrez essayer d'écrire un décodeur pour PNG (ou un autre format).
Matériaux additionnels
Si vous êtes intéressé par les détails, lisez le matériel que j'ai utilisé pour écrire l'article, ainsi que quelques travaux supplémentaires:
- Guide illustré de l'effilochage JPEG
- Un article très détaillé sur l'encodage Huffman en JPEG
- Ecrire une bibliothèque JPEG simple en C ++
- Documentation pour struct en Python 3
- Comment FB a tiré parti des connaissances JPEG
- Disposition et format JPEG
- Présentation intéressante du DoD sur la criminalistique JPEG